Решение задач по теме «Условная вероятность»

Использование теории вероятности в играх

Использование теории вероятности в науке

2.68M

Category: $mathematics$ mathematics

Решение задач по теме «Условная вероятность»

1. Решение задач по теме «Условная вероятность»

2.

Всем правит случай.
Знать бы еще, кто
правит случаем.
Станислав Ежи Лец

1
2
7
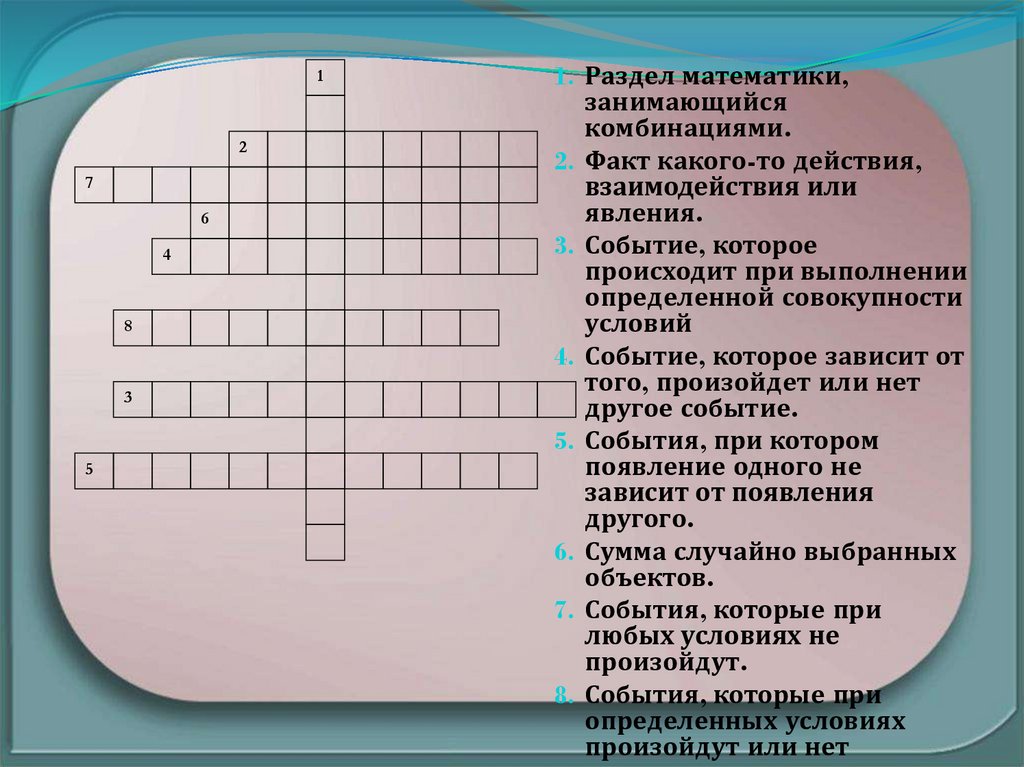
1. Раздел математики,
2.
6
4
3.
8
4.
3
5.
5
6.
7.
8.
занимающийся
комбинациями.
Факт какого-то действия,
взаимодействия или
явления.
Событие, которое
происходит при выполнении
определенной совокупности
условий
Событие, которое зависит от
того, произойдет или нет
другое событие.
События, при котором
появление одного не
зависит от появления
другого.
Сумма случайно выбранных
объектов.
События, которые при
любых условиях не
произойдут.
События, которые при
определенных условиях
произойдут или нет

4. Ответы:

1. комбинаторика
2. событие
3. достоверное
4. зависимое
5. независимые
6. выборка
7. невозможные
8. случайные

5. Свойства вероятности

1.0< P(A) < 1 ,
т.к. 0<m<n
2. P(U) = 1 ,
т.к. m=n
3. P(V) = 0,
т.к. m=0

6.

Вероятность появления одного из двух
несовместных событий равна сумме
вероятностей этих событий
Вероятность
произведения
независимых событий А и В
вычисляется по формуле:

7. Условная вероятность

Формула полной вероятности

8.

1. Три господина, придя в ресторан,
сдали в гардероб свои шляпы.
Расходились по домам они уже в
темноте и разобрали свои шляпы
наугад. Укажите невозможное
событие.
А: каждый надел свою шляпу
В: двое надели чужие шляпы, а
один – свою
Б: все надели чужие шляпы
Г: двое надели свои шляпы, а
один – чужую

9.

2. Укажите,
какое из следующих
событий случайное.
А: футбольный матч «СпартакДинамо» закончится вничью
В: 30 февраля будет дождь
Б: вы выиграете, участвуя в
беспроигрышной лотерее
Г: в полночь выпадет снег, а
через 24 часа будет светить
солнце

10.

3. Студент сдает экзамен по
математике. Укажите
достоверное событие.
А: студент получит оценку «5»
Б: экзамен перенесен на
другой день
В: студент знает ответы на все
вопросы
Г: преподаватель знает ответы
на все вопросы

11.

4. Среди 50 деталей 5
бракованных. Какова вероятность
того, что наугад взятая деталь
окажется без брака?
А: 0,1
Б: 0,5
В: 0,9
Г: 1

12.

5. Из 1000 поступивших в магазин
телевизоров 4 оказались неисправными.
Какова вероятность того, что купленный
Вами телевизор исправен?
А: 0,004
Б: 0,04
В: 0,996
Г: 1

13.

6. Набирая номер телефона, абонент забыл
последнюю его цифру и набирает его
наугад. Какова вероятность того, что номер
набран правильно?
А: 1/100
Б: 1/10
В: 1/9
Г: 1/6

14.

7. Из посаженных 80 семян огурцов
определенного сорта проросло 72.
Найдите всхожесть семян.
А: 0,1
Б: 0,5
В: 0,8
Г: 0,9

15.

8. В шкафу 10 пар ботинок с 36 по 45 размер – по
одной паре каждого размера. Какое минимальное
количество ботинок надо наугад вынуть из шкафа,
чтобы событие «из вынутых ботинок можно было
составить хотя бы одну пару» было достоверным?
А: 2
Б: 3
В: 10
Г: 11

16.

1.Три господина, придя в ресторан,
сдали в гардероб свои шляпы.
Расходились по домам они уже в
темноте и разобрали свои шляпы
наугад. Укажите невозможное
событие.
А: каждый надел свою шляпу
В: двое надели чужие шляпы, а
один – свою
Б: все надели чужие шляпы
Г: двое надели свои шляпы, а
один – чужую

17.

18.

19.

20.

21.

22.

7. Из посаженных 80 семян огурцов
определенного сорта проросло 72.
Найдите всхожесть семян.
А: 0,1
Б: 0,5
В: 0,8
Г: 0,9

23.

24.

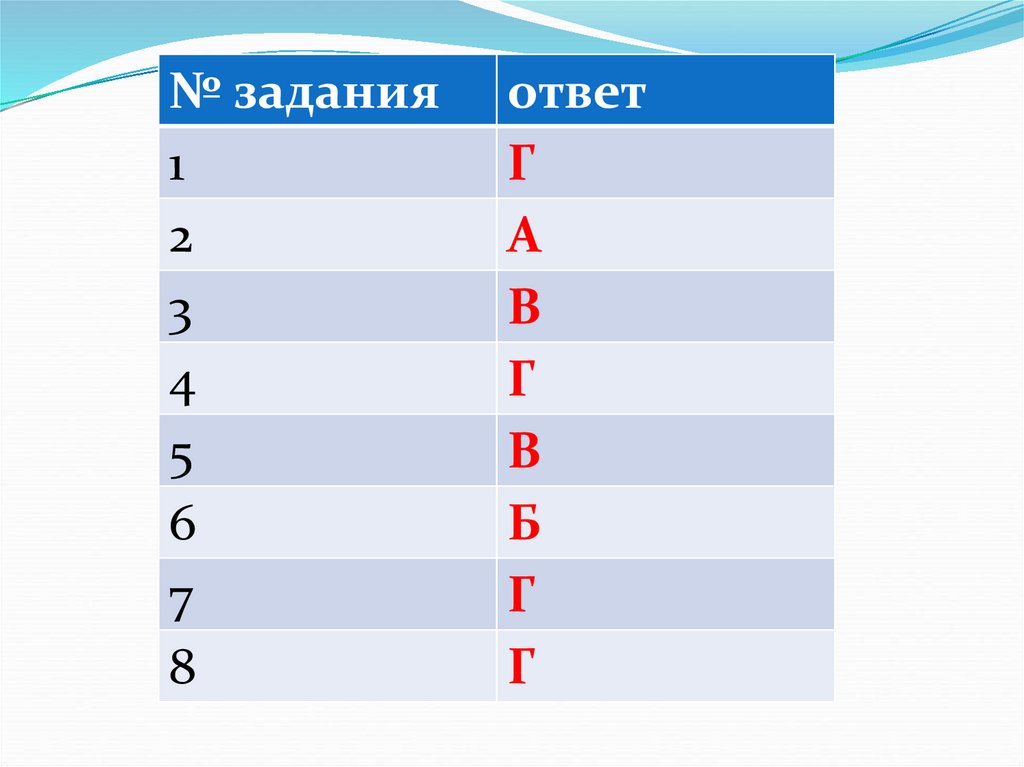
№ задания
1
2
3
4
5
6
7
8
ответ
Г
А
В
Г
В
Б
Г
Г

25.

26.

27.

Пять учеников вытягивают на экзамене пять
билетов, один из которых очень лёгкий.
Какова вероятность для каждого учащегося
вытащить удачный билет?

28.

Некий
властелин
разгневался
на
звездочёта и повелел его наказать. Однако в
последний момент властелин смягчился и решил
дать звездочёту возможность избежать наказание.
Он взял два чёрных и два белых шара и
предложил звездочёту произвольным образом
распределить их по двум урнам. Властелин
должен выбрать наугад одну из урн и наугад
вытащить из неё шар. Если шар окажется белым,
то звездочёт будет помилован, а если чёрнымнаказан. Как должен звездочёт распределить
шары по двум урнам, чтобы иметь наибольшее
число шансов избежать наказание?

29. 30. Задача Пункаре

В игорном клубе половина игроков
честные, половина – шулеры.
Вероятность вытащить из колоды дамы
равна 1/8. Для шулера эта вероятность
равна 1. Сидящий перед вами игрок
вытаскивает из колоды даму с первого
раза. С какой вероятностью перед вами
шулер?

31.

A – «из колоды вытянут даму»
B – «игрок шулер».
- «игрок честный»
P (A | B) = 1,
Если взять первого попавшегося игрока, то он
вытянет даму с вероятностью

32.

X – «игрок, вытянувший даму, – шулер»

33. Использование теории вероятности в играх

Устройства для получения набора случайных
чисел: Урны (например, ящик с шарами –
лототрон, используемый в передаче
«Спортлото»);
Кости (например, кубики, используемые при
игре в нарды);
Рулетки (круг со стрелкой, используемый в
передаче «Что? Где? Когда?»).

34. Использование теории вероятности в науке

Прогнозирование природных катастроф
(например, ожидание урагана);
Теория ошибок наблюдений;
Теория стрельбы;
Метеорология;
Статистика (например, подсчитано, что частота
рождения мальчиков 0,518, а девочек 0,482)

35.

Вероятно, будет дождь; а пока жара.
Вероятно, будем жить лучше, чем вчера.
Вероятно, вечером в доме будет свет.
Может быть - хороший день, - может быть, и нет.
Вероятно, радуга за грозою вслед
На небе появится; а пока что - нет.
Вероятно, в поезде песни будем петь,
Если вероятности выучить успеть.
Этих вероятностей в жизни пруд пруди,
Только их теорию - выучи поди!
Чтобы по теории двойку не схватить,
Эти вероятности надобно учить.

36. Домашнее задание

Творческая работа на тему:
«Вероятность вокруг нас»

37.

Спасибо за урок!

English Русский Rules