Similar presentations:
Уменьшение длины микропрограммы за счет инвертирования некоторых логических условий
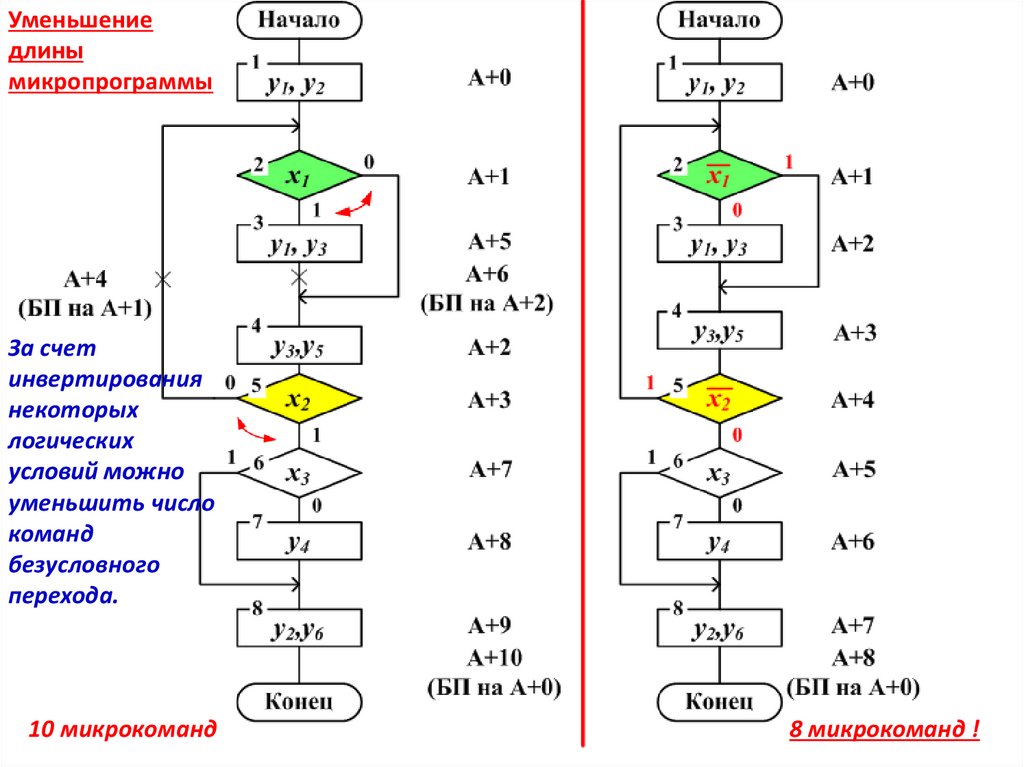
1.
Уменьшениедлины
микропрограммы
За счет
инвертирования
некоторых
логических
условий можно
уменьшить число
команд
безусловного
перехода.
10 микрокоманд
8 микрокоманд !
2.
Принудительная адресациямикрокоманд
3.
Принцип принудительной адресации МК предполагает единый формат МКтипа М.X.А. :
Адрес следующей МК определяется в предыдущей МК по правилу:
А .1, если x X 1,
Аслед
А . 0 , если x X 0.
Другими словами,
Аслед A . x X
В каждой микрокоманде (в поле A) всегда указывается адрес следующей
микрокоманды, но без последнего разряда. Последний разряд адреса
следующей команды равен значению логического условия, номер которого
указан в поле X текущей команды.
Таким образом в каждой микрокоманде задается разветвление на два
адреса: четный и нечетный.
4.
Формат МК М.X.А предполагает, что каждой МК должен соответствоватьследующий участок ГСА функционирования УА:
5.
А если в ГСА идут подряд две условные вершины?Поле М полученной микрокоманды будет нулевым.
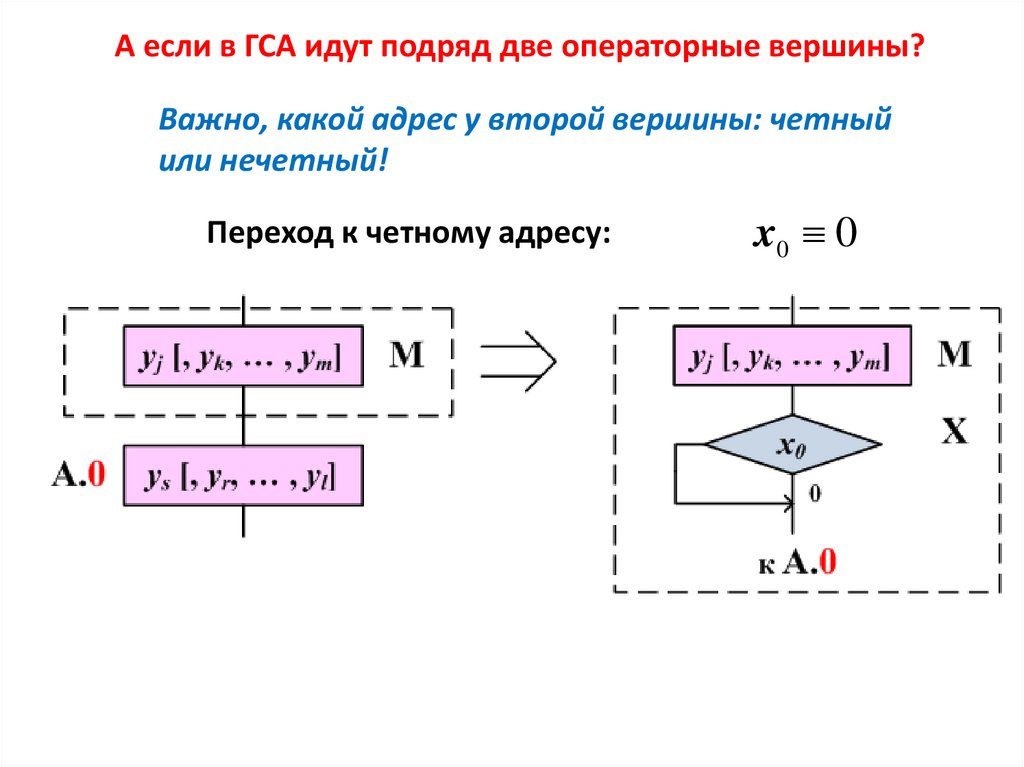
6.
А если в ГСА идут подряд две операторные вершины?Важно, какой адрес у второй вершины: четный
или нечетный!
Переход к четному адресу:
x0 0
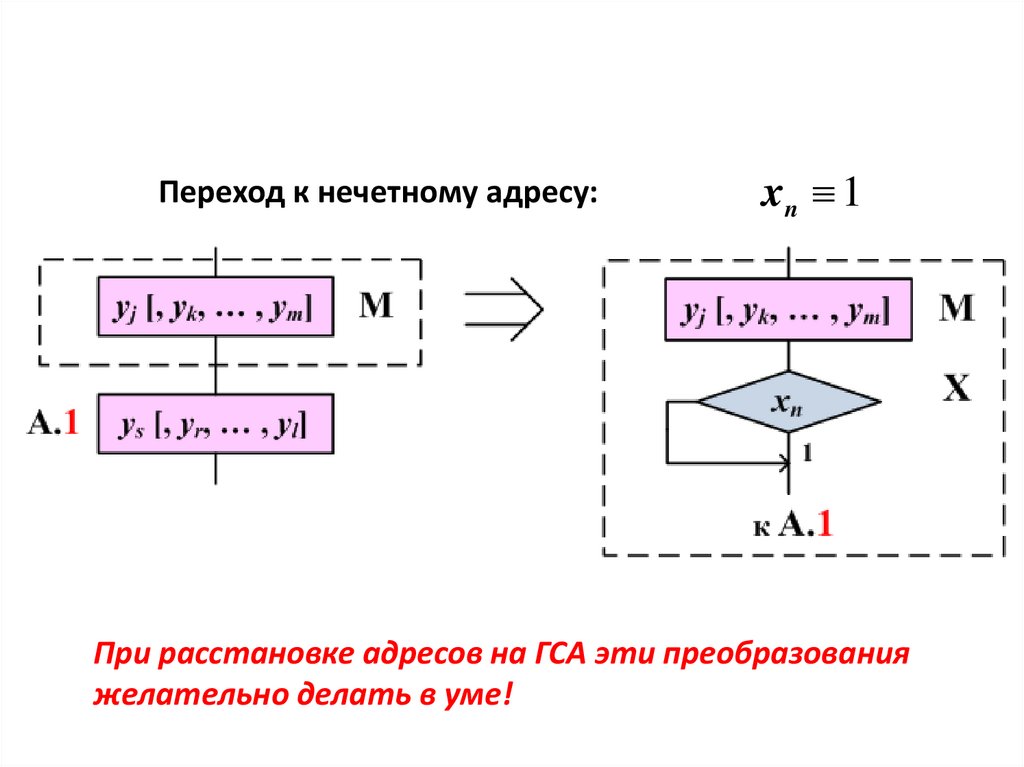
7.
Переход к нечетному адресу:xn 1
При расстановке адресов на ГСА эти преобразования
желательно делать в уме!
8.
1 этап проектирования УА –расстановка адресов
микрокоманд на ГСА
Берем свободный
парный адрес А1
А0.0
А1.0
А1.1
А3.0
x4
А0.1
Можно взять
неиспользованную
часть адреса А0
x4 1
Дублирование
МК по двум
адресам
А2.1
А2.0
x0
Зацикливаем
А0.0
А3.1
x0
x0 0
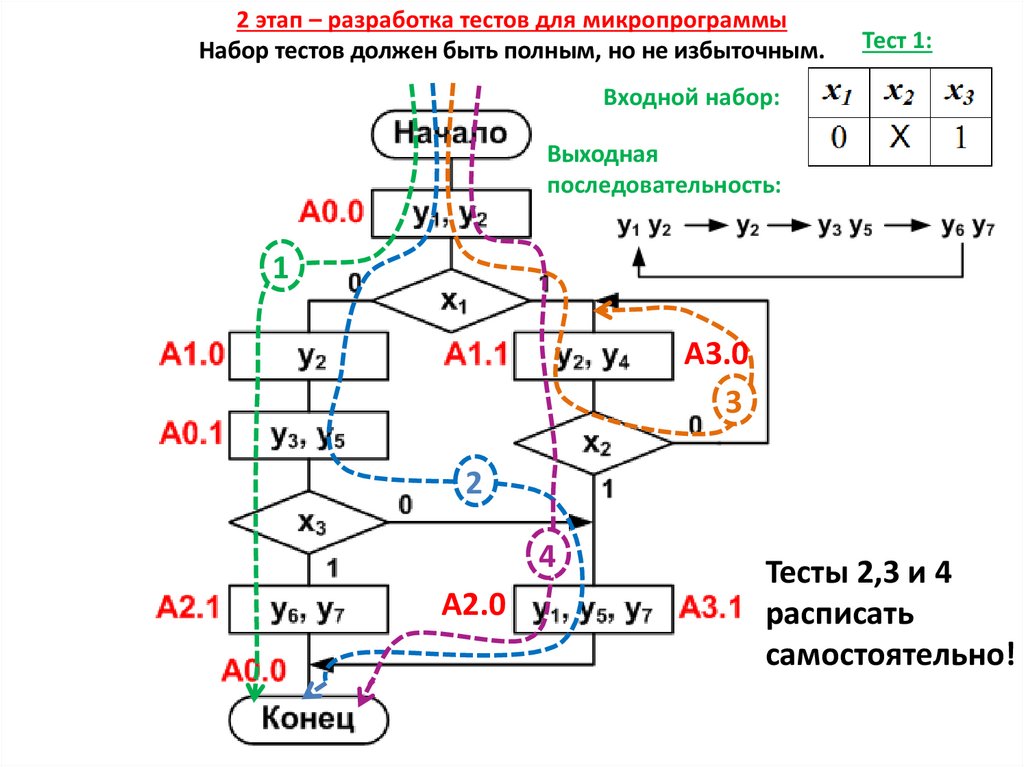
9.
2 этап – разработка тестов для микропрограммыНабор тестов должен быть полным, но не избыточным.
Тест 1:
Входной набор:
Выходная
последовательность:
1
А3.0
3
2
42
А2.0
Тесты 2,3 и 4
расписать
самостоятельно!
10.
3 этап – разработка микропрограммы в символических обозначенияхx0 0
x4 1
− используется для безусловного перехода
на четный адрес;
− используется для безусловного перехода
на нечетный адрес;
11.
4 этап – тестирование микропрограммы в условных обозначенияхМП
Тест 1:
Входной набор:
Выходная
последовательность:
Трассировка МП для теста 1
Для тестов 2, 3 и 4
сделать трассировку
микропрограммы
самостоятельно!
12.
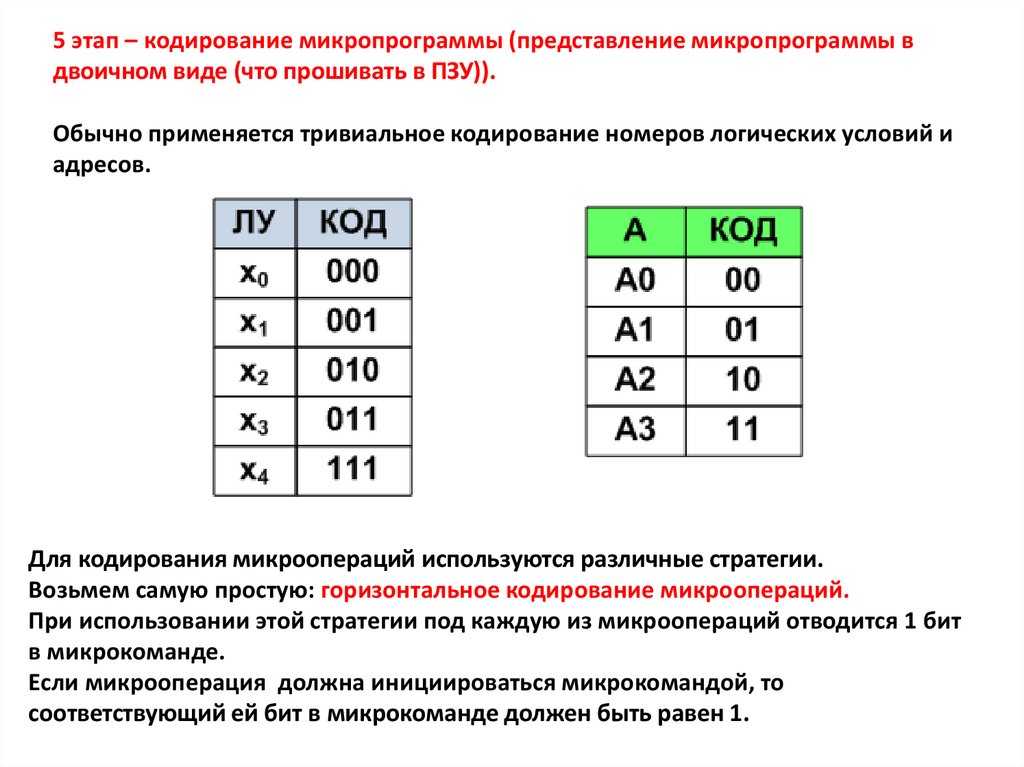
5 этап – кодирование микропрограммы (представление микропрограммы вдвоичном виде (что прошивать в ПЗУ)).
Обычно применяется тривиальное кодирование номеров логических условий и
адресов.
Для кодирования микроопераций используются различные стратегии.
Возьмем самую простую: горизонтальное кодирование микроопераций.
При использовании этой стратегии под каждую из микроопераций отводится 1 бит
в микрокоманде.
Если микрооперация должна инициироваться микрокомандой, то
соответствующий ей бит в микрокоманде должен быть равен 1.
13.
Микропрограмма всимволическом виде
Микропрограмма в двоичном виде (прошивка ПЗУ)
Тестирование производится с помощью эмулятора
УА с программируемой логикой (ЛР3 – ЛР6).
14.
СРАВНЕНИЕМП для УА с естественной
адресацией МК
МП для УА с принудительной
адресацией МК
12x8=96 битов
Какой вариант предпочтете?
8x12=96 битов
При фиксированном такте работы УА
микропрограмма с использованием
принудительной адресации будет
выполняться быстрее за счет
отсутствия условных команд.
15.
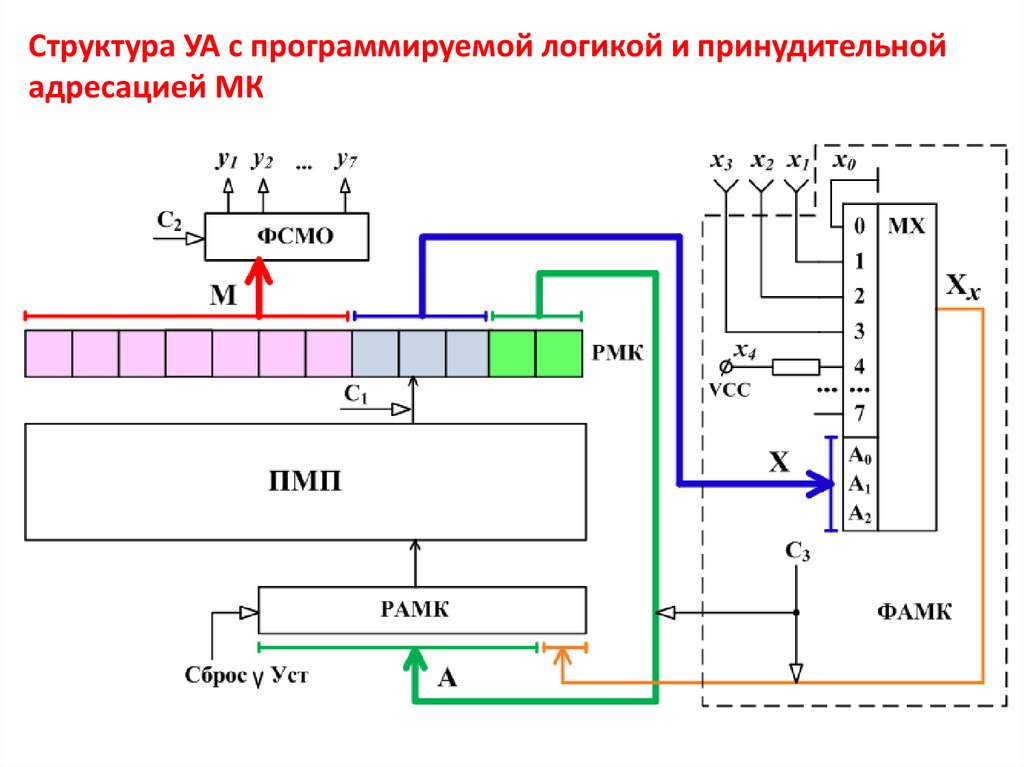
Структура УА с программируемой логикой и принудительнойадресацией МК
16.
Структура формирователя сигналов микроопераций (ФМСО)при горизонтальном кодировании микроопераций
В отличие от аналогичного формирователя для УА с естественной адресацией,
здесь используются двухвходовые (а не трехвходовые) элементы «И», т.к. не
нужно домножать на инверсию бита-маркера.
17.
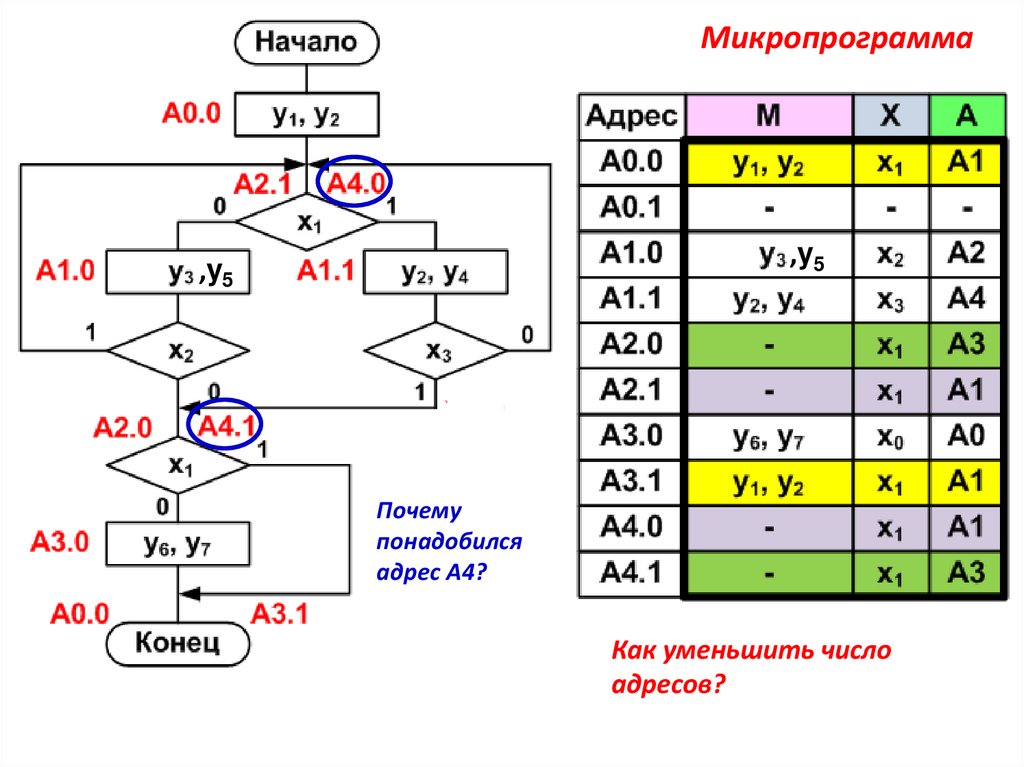
Пример с идущими подряд условными вершинамиА0.0
А2.1
А1.0
А2.0
,y5
А4.0
А1.1
А4.1
А3.0
А0.0
А3.1
18.
Микропрограмма,y5
,y5
Почему
понадобился
адрес А4?
Как уменьшить число
адресов?
19.
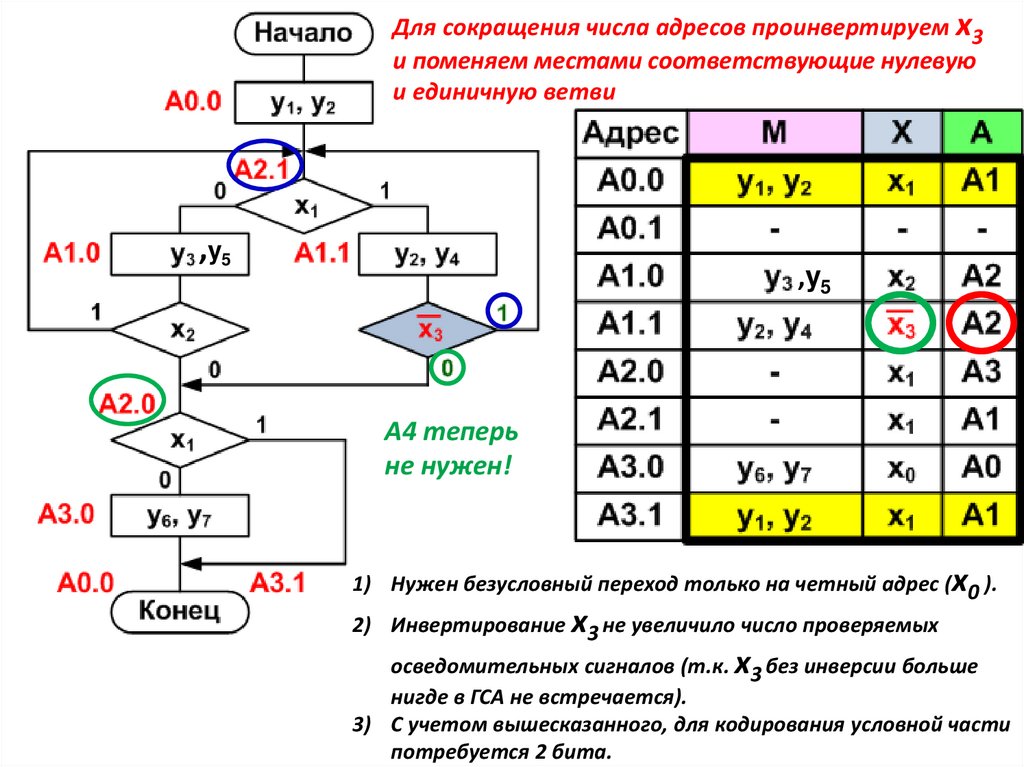
Для сокращения числа адресов проинвертируем х3и поменяем местами соответствующие нулевую
и единичную ветви
,y5
,y5
А4 теперь
не нужен!
1) Нужен безусловный переход только на четный адрес (x0 ).
2) Инвертирование x3 не увеличило число проверяемых
осведомительных сигналов (т.к. х3 без инверсии больше
нигде в ГСА не встречается).
3) С учетом вышесказанного, для кодирования условной части
потребуется 2 бита.
20.
Применяя описанный подход, нужно иметь в виду, что инвертирование некоторыхосведомительных сигналов может увеличить (если в микропрограмме станет
анализироваться и прямое и инверсное значение некоторого осведомительного
сигнала) число входов мультиплексора, на которые подаются иксы. Если при этом не
увеличивается число адресных входов мультиплексора (число битов, кодирующих
номер логического условия), то ничего страшного.
Иначе, увеличивается (незначительно) длина микрокоманды и сложность
мультиплексора (например, вместо мультиплексора 2х4 может потребоваться
мультиплексор 3х8).
Но при этом можно получить существенный выигрыш в длине микропрограммы.
Выигрыш в длине микропрограммы не обязательно приводит к экономии числа
микросхем ПЗУ, необходимых для хранения микропрограммы. Например, если мы
сократили микропрограмму с 64 микрокоманд (адресов) до 50, нам все равно
потребуется 2 линейки ПЗУ 32x8.
Все ваши решения должны быть продуманы и обоснованы!
21.
Стратегии кодирования микроопераций1) Горизонтальное кодирование микроопераций (самая длинная
операционная часть МК, самый простой ФСМО).
2) Вертикальное кодирование микроопераций (самая короткая
операционная часть МК, самый сложный ФСМО).
3) Горизонтально-вертикальое кодирование МО (совмещает идеи первых
двух методов).
4) Вертикально-горизонтальное кодирование МО (совмещает идеи
первых двух методов).
Третий и четвертый метод, в отличие от первых двух
(«крайних»), позволяют достичь некоторого компромисса между
длиной операционной части МК и структурой формирователя
сигналов микроопераций (ФСМО)
22.
Горизонтальное кодирование микроопераций(частично уже рассмотрено)
При горизонтальном способе кодирования МО под каждый управляющий
сигнал yi (i=1, 2,…, m) в операционной (М) части МК выделяется один
(свой) двоичный разряд, что позволяет в рамках одной МК формировать
любые сочетания управляющих сигналов. ФСМО для такого способа
кодирования обладает наименьшей стоимостью и минимальным
временем срабатывания.
23.
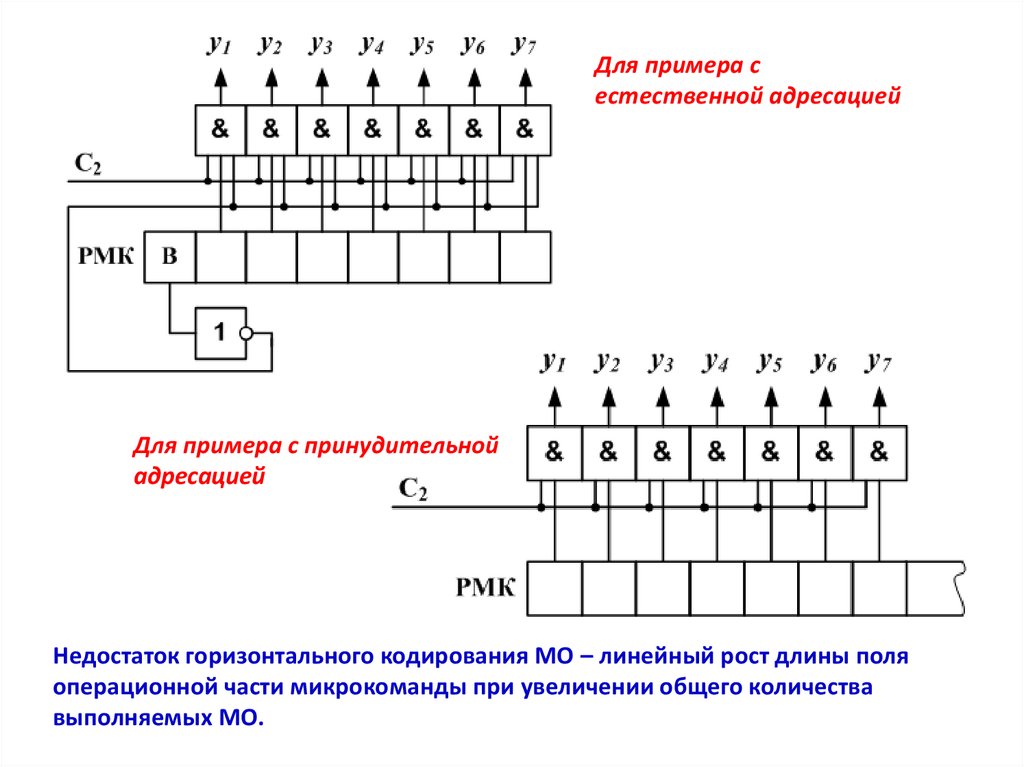
Для примера сестественной адресацией
Для примера с принудительной
адресацией
Недостаток горизонтального кодирования МО – линейный рост длины поля
операционной части микрокоманды при увеличении общего количества
выполняемых МО.
24.
Сокращение длины операционной части МК при горизонтальном кодированииНа ГСА
символами Yi
обозначены
микрокоманды
Информация, о микрооперациях,
присутствующих в каждой
микрокоманде, сведена в таблицу.
y4 y2
y6 y1
25.
Структура ФСМОy6 y1
y4 y2
26.
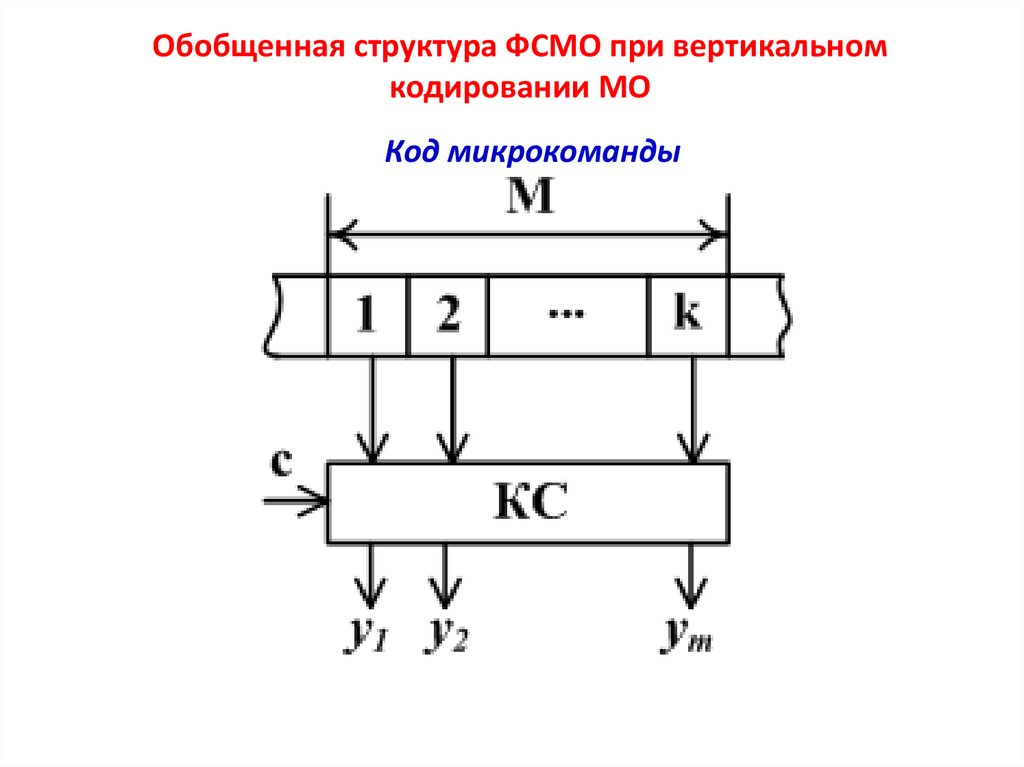
Вертикальное кодирование микрооперацийПри вертикальном способе кодирования каждой различной совокупности
МО, включенной в ту или иную МК, присваивается позиционный код
~ – количество различимых
~ , где m
минимальной длины k log 2 m
по операционной части МК. ФСМО в этом случае представляет собой
комбинационную схему (КС), реализующую m булевых функций от k
переменных.
При вертикальном способе кодирования кодируются не микрооперации,
а микрокоманды.
Каждой отличимой от других микрокоманде ставится в соответствие
позиционный код.
В разных местах ГСА могут встречаться одни и те же микрокоманды, т.е.
микрокоманды, содержащие один и тот же набор МО. Такие
микрокоманды будем обозначать одним и тем же символом Yi.
Различные микрокоманды (отличающиеся по наборам микроопераций)
будем обозначать символами Y с отличающимися индексами.
27.
Обобщенная структура ФСМО при вертикальномкодировании МО
Код микрокоманды
28.
Вертикальный принцип кодирования МО предполагает, чтокаждая МК кодируется кодом минимальной длины, а для
расшифровки используемых кодов необходимо разработать
комбинационную схему, реализующую систему булевых
функций.
Для упрощения булевых функций, определяющих конкретные
МО, используется принцип соседнего кодирования: наиболее
«близкие» по микрооперациям микрокоманды кодируются
соседними кодами (т.е. кодами, отличающимися на 1 бит).
Для данного примера можно предложить следующее
кодирование:
29.
Система булевых функций:y1 Y1 Y2 M1 M 2 M3 M1 M 2 M3 M1 M 2 ;
y2 Y1 Y5 M1 M 2 M3 M1 M 2 M3 M 2 M3;
y3 Y2 Y3 M1 M 2 M3 M1 M 2 M3 M1 M3;
y4 Y4 M1 M 2 M3 ;
y6 Y5 M1 M 2 M3;
y5 Y3 M1 M 2 M3;
Склеивание
происходит за
счет соседнего
кодирования
30.
Схема ФСМОЕсли используется естественная адресация МК, то каждый элемент «И» должен
иметь еще один вход для домножения на инверсию бита-маркера
31.
Можно упростить задачу (не утруждаться соседним кодированием;-), если вкачестве схемы, раскодирующей микрокоманды использовать дешифратор.
Второй способ построения ФСМО
Тривиальное кодирование операционных микрокоманд
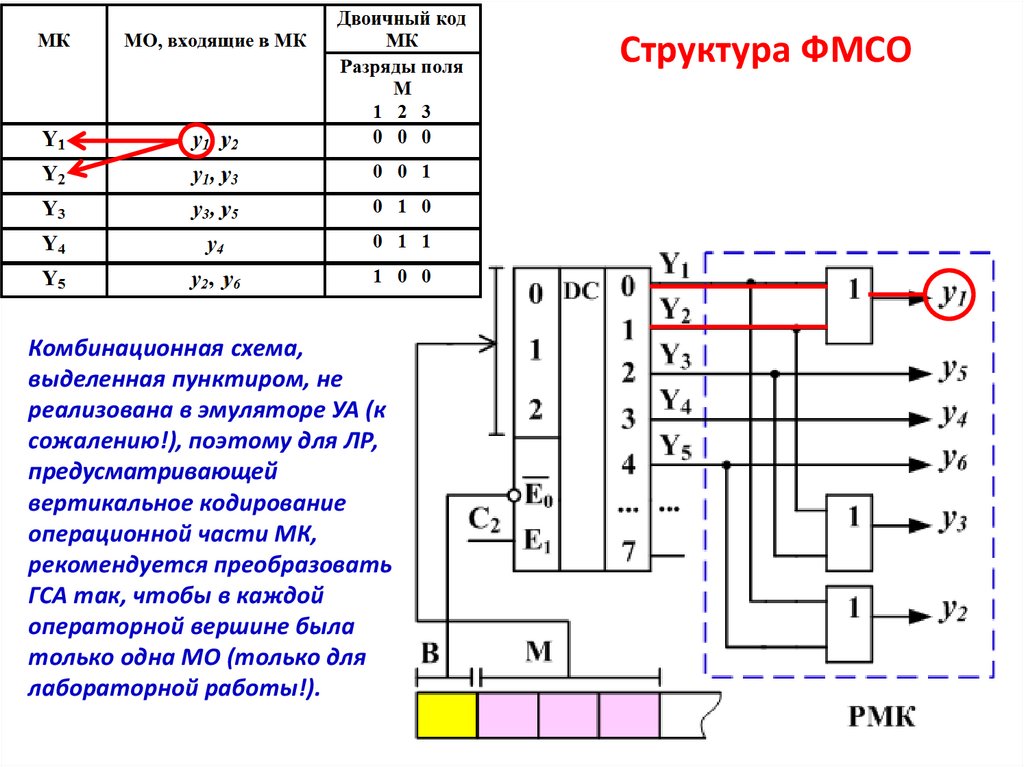
32.
Структура ФМСОКомбинационная схема,
выделенная пунктиром, не
реализована в эмуляторе УА (к
сожалению!), поэтому для ЛР,
предусматривающей
вертикальное кодирование
операционной части МК,
рекомендуется преобразовать
ГСА так, чтобы в каждой
операторной вершине была
только одна МО (только для
лабораторной работы!).
33.
Полевые стратегиикодирования
микроопераций
(сочетают в себе элементы
горизонтального и вертикального
кодирования)
34.
1. Горизонтально-вертикальное кодирование МО(раздельными независимыми полями,
подмножествами несовместимых операций)
Обобщенная структура ФСМО
Идея: разбить все
множество
микроопераций М на
подмножества
несовместимых МО.
Тогда в МК будет
присутствовать
только одна МО из
того или иного
подмножества или ни
одной.
Под несовместимыми
будем понимать МО,
которые никогда не
встречаются вместе
в блоках ГСА.
Каждому управляющему сигналу,
включенному в подмножество
сопоставляется позиционный код (и,
соответственно, выход дешифратора).
Полностью нулевой код говорит об
отсутствии в МК управляющего сигнала
из данного подмножества.
35.
Для осуществления горизонтально-вертикальногопринципа кодирования МО необходимо разбить все
множество МО на подмножества несовместимых МО. Для
этого удобно построить матрицу несовместимости МО.
В этой матрице на пересечении строк и столбцов,
соответствующих микрооперациям, которые упомянуты в
одной микрокоманде (операторной вершине ГСА) ставятся
нули, затем остальные клетки заполняются единицами.
Таким образом единичное значение элемента матрицы
задает отношение несовместимости соответствующих МО.
Матрица симметрична относительно главной диагонали,
поэтому можно ограничиться построением только нижней
части матрицы.
36.
Матрица несовместимости МОСоставляются подмножества МО, в каждое из
которых входят только несовместимые между собой МО
(не встречающиеся в одной микрокоманде).
Учитывая, что расшифровывать коды будут
дешифраторы, мощность каждого подмножества должна
стремиться к величине 2k-1, где k=1, 2, … (количество
битов, используемых для кодирования управляющего
сигнала (y) в соответствующем подмножестве).
37.
Шаг 1. Открываем первое множество.Добавляем в него микрооперацию y1.
1) y1
Шаг 2. Пытаемся добавить в первое
подмножество y2. Это невозможно, так как
y2 совместима с y1 (эта информация
получена из матрицы несовместимости).
Открываем второе подмножество.
Добавляем в него y2.
1) y1
2) y2
Шаг 3. Пытаемся добавить у3 в первое
подмножество. Это невозможно, так как у3
совместима с y1. Добавляем у3 во второе
подмножество. Это возможно, так как у3
несовместима с y2.
1) y1
2) y2 , у3
Для получения подмножеств
можно использовать метод
прямого включения
микроопераций. Этот метод
проиллюстрирован на
рассматриваемом примере.
38.
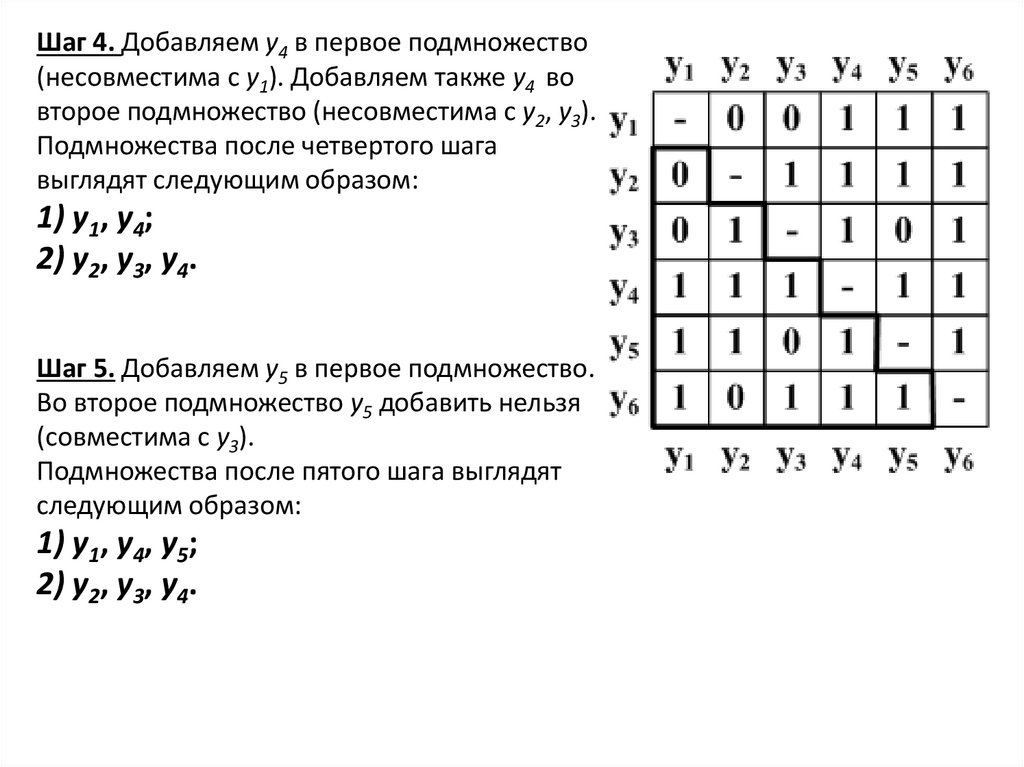
Шаг 4. Добавляем у4 в первое подмножество(несовместима с y1). Добавляем также у4 во
второе подмножество (несовместима с y2, у3).
Подмножества после четвертого шага
выглядят следующим образом:
1) y1, у4;
2) y2, у3, у4.
Шаг 5. Добавляем у5 в первое подмножество.
Во второе подмножество у5 добавить нельзя
(совместима с у3).
Подмножества после пятого шага выглядят
следующим образом:
1) y1, у4, у5;
2) y2, у3, у4.
39.
Шаг 6. Добавляем у6 в первоеподмножество. Во второе
подмножество у6 добавить
нельзя (совместима с y2).
Подмножества после шестого
шага выглядят следующим
образом:
1) y1, у4, у5, у6;
2) y2, у3, у4.
Шаг 7. Убираем у4 из первого
подмножества. Окончательный
результат:
1) y1, у5, у6;
2) y2, у3, у4.
Мощность полученных подмножеств равна
3= 22-1. Каждое подмножество будет
представлено двумя двоичными
разрядами. Комбинация 00 в этих разрядах
будет означать, что в МК не присутствуют
МО из данного подмножества, остальные
три комбинации будут сопоставлены
единичным значениям соответствующих
управляющих сигналов, входящих в
данное подмножество.
40.
Метод прямого включения является приближенным и вобщем случае дает не единственное решение. Результат
разбиения на подмножества в более сложных, чем
приведенный пример, случаях зависит от порядка
рассмотрения управляющих сигналов.
Из нескольких вариантов разбиения на подмножества
разработчик может выбрать лучший по критерию
минимальной длины операционной части МК или по
критерию упрощения структуры ФСМО.
41.
МО, включенную в несколько подмножеств, необходимо оставить только в одномиз них. На решение разработчика в этом случае могут повлиять следующие
соображения:
1) возможность сократить длину операционной части МК (по этому критерию в
нашем примере исключена из первого подмножества и оставлена во втором
подмножестве у4, что сократило число двоичных разрядов, необходимых для
кодирования первого подмножества и не увеличило число разрядов, кодирующих
второе подмножество):
Дешифратор 2х4
1) y , у , у , у ;
1
4
5
2) y2, у3, у4.
6
Дешифратор 2х4
2) возможность упростить структуру ФСМО (когда присутствие некоторой МО в
одном подмножестве не увеличивает число двоичных разрядов, кодирующих
данное подмножество, а исключение той же МО из другого подмножества приводит
к горизонтальному кодированию в этом подмножестве – число разрядов,
кодирующих подмножество, равно числу микроопераций в подмножестве)
1) y1, у4, у5, у6 , у7 , у8 , у9 ;
2) y2, у3, у9.
Дешифратор 3х8
2 элемента «И» вместо дешифратора 2х4
42.
3)при исключении некоторой МО из подмножества (приусловии, что она останется в каком-либо другом
подмножестве), в данное подмножество можно добавить
другую МО, совместимую с исключенной, но не совместимую
с оставшимися в подмножестве МО.
Допустим, на очередном шаге микрооперации по
подмножествам распределились так:
1) y1, у4, у5 ,
2) y2, у3, у5 ,
и осталось включить последнюю МО у6 , которая совместима
с у5 и y1 и не совместима с y2, у3. Тогда выгодно убрать у5 из
второго подмножества, чтобы можно было в него добавить у6.
1) y1, у4, у5 ,
2) y2, у3, у6
43.
Вернемся к нашему примеруПо сравнению с горизонтальным кодированием
удалось сократить длину операционной части МК на
2 разряда.
44.
Наличие кода 00 в М1 или М2говорит об отсутствии в МК
микрооперации из этого
подмножества
Структура ФСМО
!
!
Что изменится для
принудительной
адресации?
При естественной адресации МК
45.
Структура ФСМО при использованиипринудительной адресации МК
Дешифратор работает (расшифровывает позиционный код, поданный на входы 0,
1, только если выполняется условие:
E0 E1 1
46.
1. Вертикально-горизонтальное кодирование МОкодирование (несовместимыми
подмножествами микроопераций)
Идея: разбить все множество микроопераций М на
подмножества. В подмножество включать только
совместимые микрооперации. Сами подмножества
не должны пересекаться (задача разбиения графа
на несвязанные подграфы).
Тогда в каждой МК будет присутствовать только
одно из подмножеств. МО внутри подмножества
можно кодировать горизонтальным кодом
(мощность (длина) подмножества существенно
меньше мощности множества М).
Если МО в МП сильно связаны, то бывает трудно
осуществить такое разбиение. Надо что-то
предпринять!
47.
Итак, при использовании вертикально-горизонтальногопринципа кодирования МО необходимо выделить
подмножества совместимых МО и обеспечить при этом
несовместимость сформированных подмножеств (ни одна
МО одного подмножества не должна быть совместима с
какой-либо МО любого другого подмножества).
Строим граф совместимости МО. На этом графе МО,
которые встречаются в одной МК, соединяются ребром.
Граф совместимости МО
(2 связи)
(2 связи)
Считаем связи!
(2 связи)
(нет связей)
(1 связь)
(1 связь)
Почти все МО связаны с другими МО. Как же
осуществить разбиение на несвязные подграфы?
48.
Для формирования несовместимых подмножеств (подграфов) с приблизительноодинаковой мощностью выделяют в универсальную группу МО, имеющие
наибольшее количество связей с другими МО. В примере этими МО могут быть y1
и у3. Если обе эти МО выделить в универсальную группу (поле М1), то на графе
совместимости останутся четыре МО.
Биты под МО универсальной
группы будут выделены в
каждой МК (УГ кодируется
горизонтально)
Оставшиеся МО разбиваем на
2 подмножества (объясните,
почему именно так?)
Чем больше «свободных»
сигналов МО оказалось, тем
лучше – их можно включать в
любое подмножество ( в какое
удобно, чтобы мощность
подмножеств была
приблизительно одинаковой).
49.
В универсальную группу (поле М1) выделили y1 и у3.В первое подмножество включили y2, у6, во второе подмножество – у4 и у5.
Подмножества будут фиксироваться в поле M3. Способ кодирования МО в полях
М1 и М3 – горизонтальный.
Идентифицирующее поле М2 будет содержать двоичный позиционный код
номера подмножества. Для полученного разбиения это поле будет
одноразрядным.
Вертикально-горизонтальное
кодирование МО в МК
В результате такого кодирования МО удалось сократить длину операционной части
МК по сравнению с горизонтальным кодированием на один разряд. В более
сложных микропрограммах с большим количеством микроопераций можно достичь
более существенного сокращения.
50.
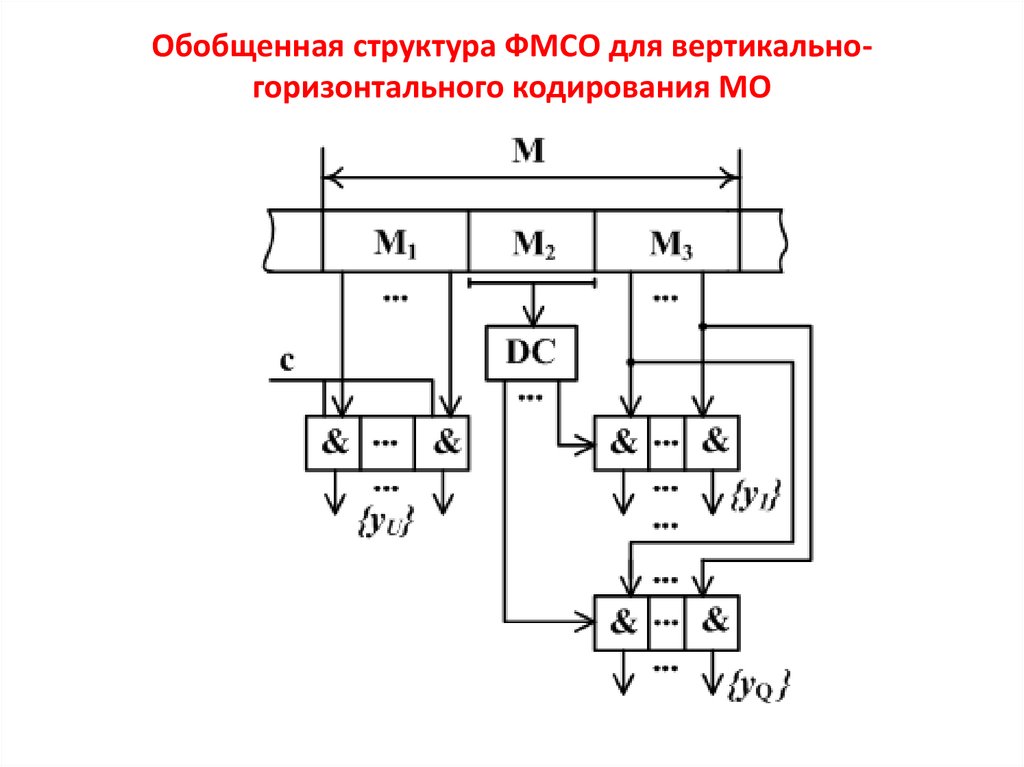
Структура ФМСО для рассмотренного примера51.
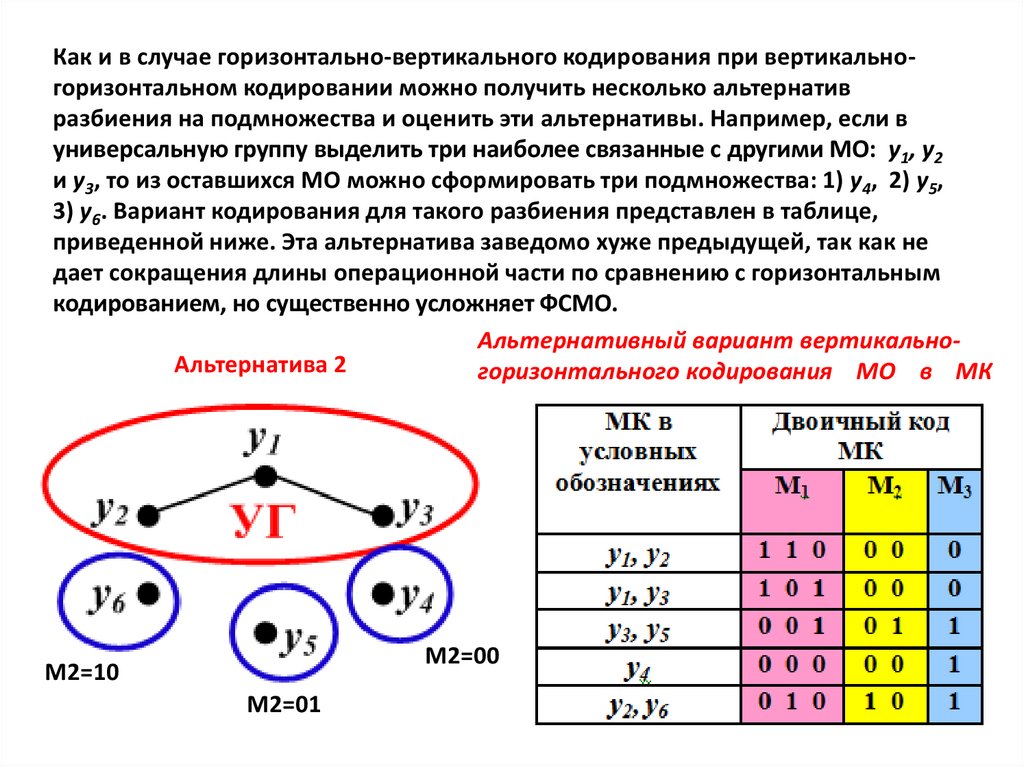
Как и в случае горизонтально-вертикального кодирования при вертикальногоризонтальном кодировании можно получить несколько альтернативразбиения на подмножества и оценить эти альтернативы. Например, если в
универсальную группу выделить три наиболее связанные с другими МО: y1, y2
и у3, то из оставшихся МО можно сформировать три подмножества: 1) у4, 2) у5,
3) у6. Вариант кодирования для такого разбиения представлен в таблице,
приведенной ниже. Эта альтернатива заведомо хуже предыдущей, так как не
дает сокращения длины операционной части по сравнению с горизонтальным
кодированием, но существенно усложняет ФСМО.
Альтернативный вариант вертикальноАльтернатива 2
горизонтального кодирования МО в МК
М2=00
М2=10
М2=01
52.
Альтернатива 31+1+3=5 - эта альтернатива
ничем не лучше первой
Альтернатива 4
1+2+2=5 - эта альтернатива хуже
первой, т.к. усложняется ФСМО
(нужен дешифратор номера
подмножества)
Рассмотрев возможные альтернативы, оценив для
каждой альтернативы длину операционной части МК
и сложность ФСМО, выбираем альтернативу 1 (самый
первый вариант вертикально-горизонтального
кодирования!







































 informatics
informatics








