Комбинированный метод хорд и касательных

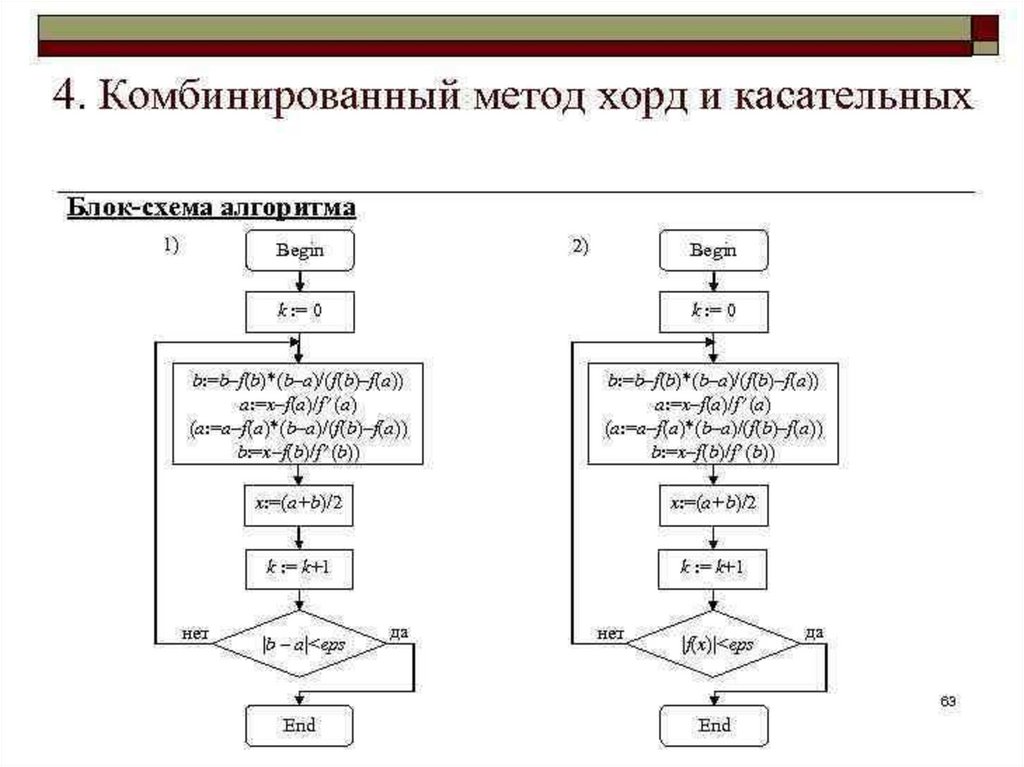
1. Комбинированный метод хорд и касательных

Материал скопирован с сайта
https://ppt-online.org/127294

2. Комбинированный метод хорд и касательных

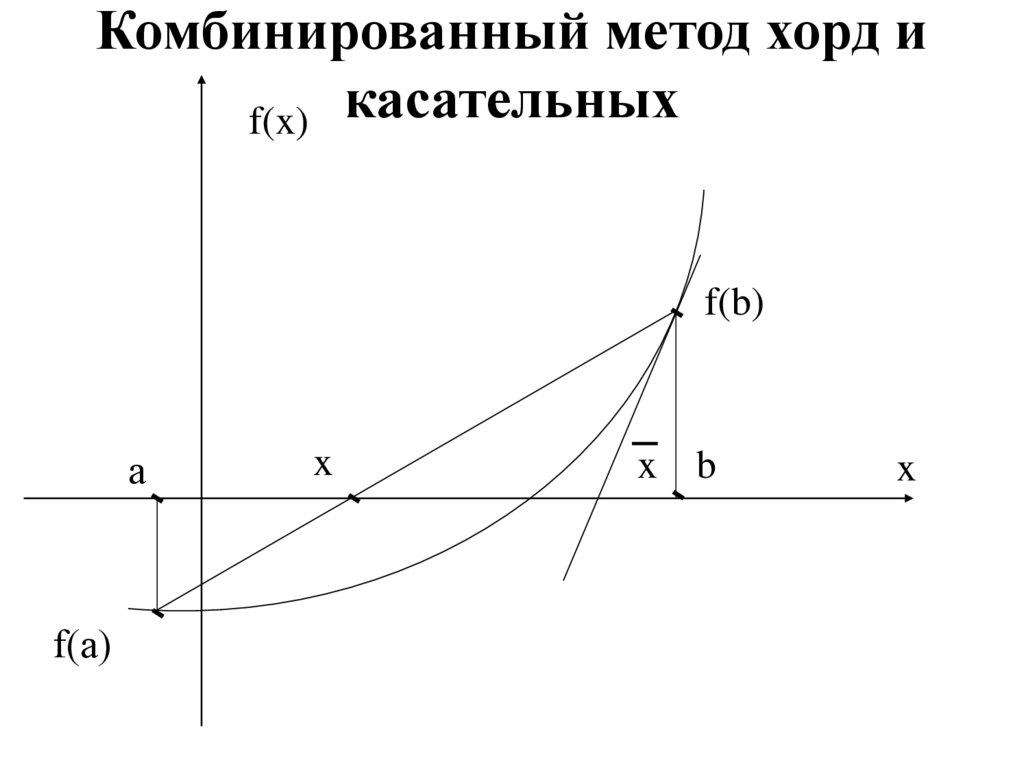
Комбинированный метод хорд и
f(x) касательных
f(b)
а
f(а)
x
x b
x

3. Суть метода:

Предположим:
1.
Что функция на интервале a; b определена и
на концах этого отрезка принимает значения разных
знаков, т.е. f (a ) * f (b) 0
2.
Что на отрезке a; b вторая производная f ( x )
определена и не меняет знак. Тогда приближения к
корню, полученные методом хорд и методом
касательных, будут на любом шаге расположены по
разные стороны от корня.

4.

1.В качестве начальной точки для
получения приближений по методу касательных
выберем тот конец отрезка a; b , для которого
выполняется условие f ( x0 ) f ( x0 ) 0 и обозначим
его x , второй конец отрезка a; b обозначим x .
2.Вычислим новые значения x и x :
a f (b) b f (a)
f ( xn )
x
xn 1 xn
f (b) f (a)
f ( xn )
3.Если x x E , то задача решена,
за приближенное значение корня можно принять
величину X x x
. В противном случае
2
переходим к пункту 2.

5.

f(x)
f(b)
а
x
x
b
x
f(а)

6. Пример:

Задана функция: f ( x ) x 3 2 x 2 4 x 7 ;
2
f
(
x
)
3
x
4 x 4;
Находим производную:
Определяем корни:
2 4 12 2 4
x1,2
3
2
x 1 ; x 2 2.
3
3
;
Составляем таблицу знаков функции :
х
-
2
Знак f(x)
-
+
3
2
+
-
+
Уравнение имеет три действительных корня:
x1 ; 2 ; x2 2 ; 2 ; x3 2;
3
3

7.

Уменьшим промежутки, содержащие корни:
х
-2
-1
0
1
2
3
Знак
f(x)
-
+
+
+
-
+
Значит, x1 2; 1 ; x2 1; 2 ; x3 2; 3 .
Уточним корни:
1. x1 2; 1 ; .
f ( 2) 0; f ( 1) 0; f ( x) 6x 4
При
2 x 1
f ( x) 0

8.

Для расчетов принимаем формулы:
f ( xn )
xn 1 xn
;
f ( xn )
f ( xn )( xn xn )
xn 1 xn
f ( xn ) f ( xn )
Полагаем, что
x0 2; x0 1
Обозначим :
f ( xn )
f ( xn )
h1n
; h2 n
( xn x )
f ( xn )
f ( xn ) f ( xn )

9.

xn
n
0
xn
-2
-1
xn xn
f ( xn )
f ( x n )
f ( xn )
1
1
2
Т.к. x x E
x1 1,935
, вычисления прекращаем,
f ( x1) 0,0001
h1n
h2 n

10.

2. x2 1; 2 ;
при
1 x 2
f (1) 0; f (2) 0; f ( x) 0 Для расчетов применяем те
же формулы, полагая
x3 2; 3 .
x0 1; x0 2
2 x 3
f (2) 0; f (3) 0; f ( x) 0
3.
при
Для расчетов применяем формулы:
f ( xn )
xn 1 xn
;
f ( xn )
Полагаем, что
Обозначим
f ( xn )( xn xn )
xn 1 xn
f ( xn ) f ( xn )
x0 2; x0 3
f ( xn )( xn x )
f ( xn )
h1n
; h2 n
.
f ( xn ) f ( xn )
f ( xn )

11.

n
0
xn
xn
2
3
xn xn
f ( xn )
f ( xn )
1
1
2
x x E
x1 2,473
f ( x1) 0,0001
f ( xn )
h1n
h2 n

12.

13. Спасибо за внимание!