Численные методы

1. Дисциплина Численные методы Материал скопирован с сайта https://ppt-online.org/128928

2. Метод касательных (метод Ньютона)

Исходные данные для реализации метода:
1.
2.
3.
4.
f(x)=0
f ’(x)
x0
E

3.

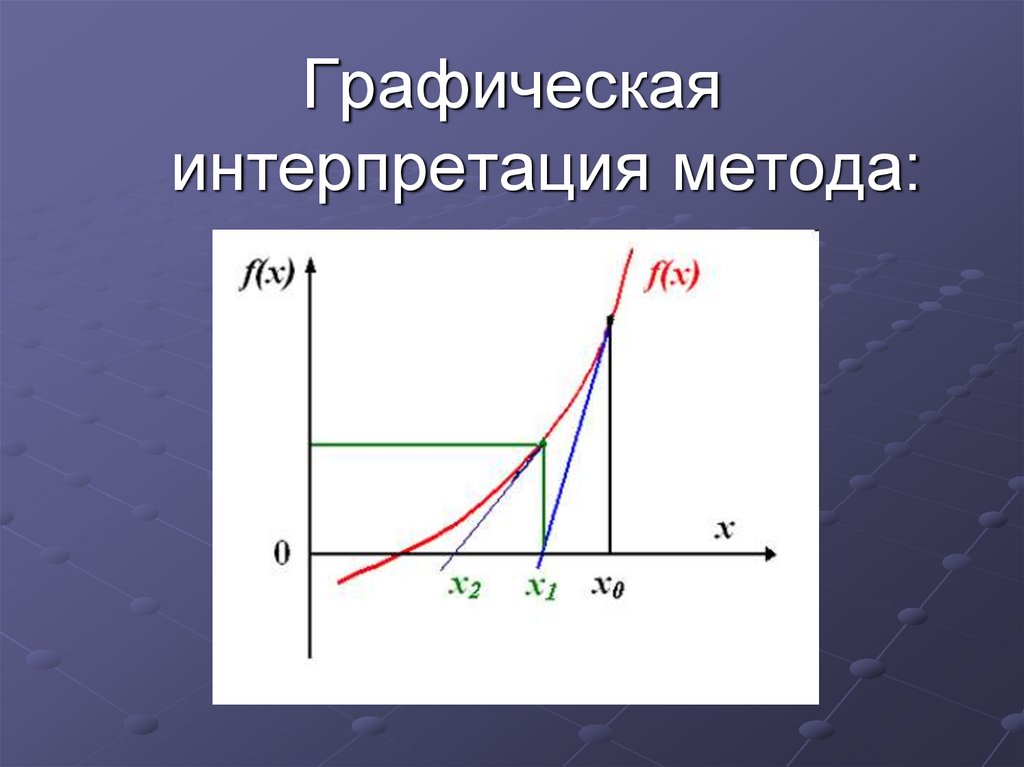
Алгоритм метода:
В точке x0 к графику функции f(x) проводится касательная.
Находится более точное значение x – это точка пересечения
касательной с осью абсцисс ОХ.
Таким образом каждая последующая точка будет лежать ближе к
истинному решению, чем предыдущая.
Последующая точка рассчитывается через предыдущую по
формуле
1.
2.
xi+1=xi-f(xi)/f ’(xi)
Процесс повторяется до тех пор, пока разность между
последующей и предыдущей точкой не станет меньше
величины точности Е
|xi+1-xi|<E
В этом случае за корень уравнения можно принять последнюю
найденную точку xi.

4.

Графическая
интерпретация метода:

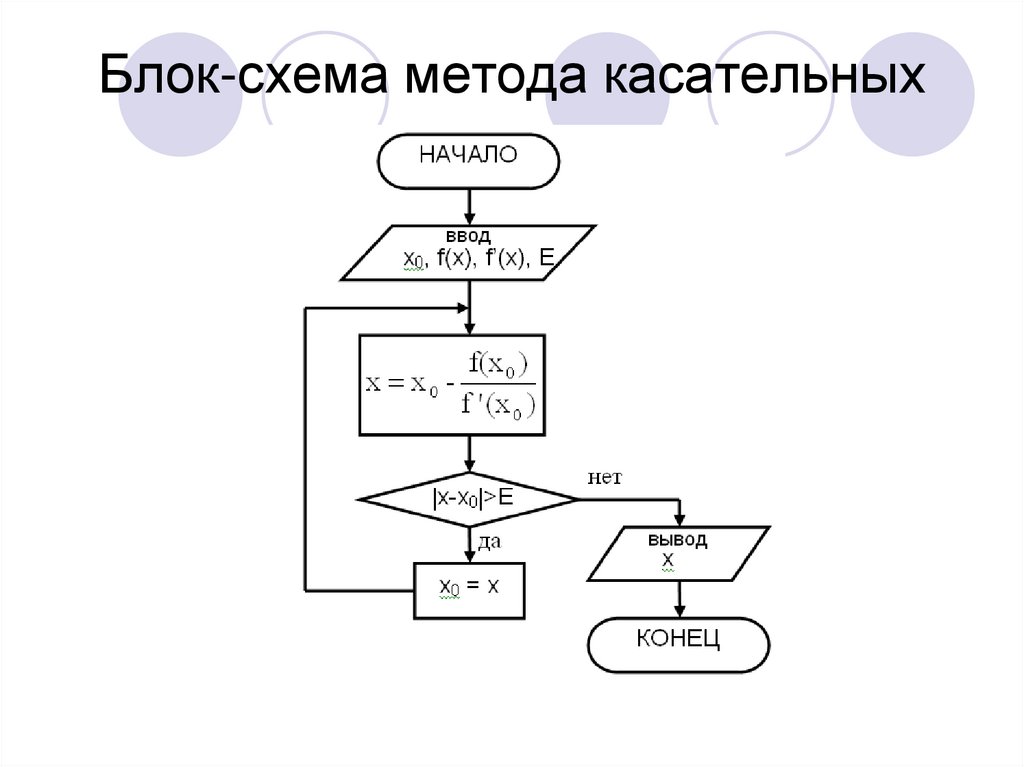
5. Блок-схема метода касательных

6.

ДОСТОИНСТВО метода
1. Высокая скорость сходимости
НЕДОСТАТКИ метода
1. Необходимость задавать
производную функции в
аналитическом виде
2. Метод является неустойчивым

7. Метод секущих

Метод секущих является модификацией
метода касательных
Исходные данные для реализации метода:
1. f(x)
2. x0
3. E

8.

Алгоритм метода:
Алгоритм аналогичен предыдущему методу, но
производная функции вычисляется по
приближенной формуле:
f
f ( x x) f ( x)
f ' ( x) lim
x 0 x
x
где x – малая величина. Как правило за эту
величину принимают величину точности Е:
f ( xi )
f ( xi ) x
f ( xi ) E
xi 1 xi
xi
xi
f ' ( xi )
f ( x x) f ( x)
f ( x E ) f ( x)

9.

ДОСТОИНСТВА метода
1. Высокая скорость сходимости
2. Нет необходимости задавать
производную функции в
аналитическом виде
НЕДОСТАТОК метода
1. Метод является неустойчивым