Цилиндрические зубчатые передачи

1.

ТЕМА «ЦИЛИНДРИЧЕСКИЕ
ЗУБЧАТЫЕ ПЕРЕДАЧИ»
Дудко О.Н.
Преподаватель ЛК ГрГУ им. Я.Купалы

2.

ЦЕЛЬ УРОКА:
Ознакомиться с видами цилиндрических
зубчатых передач и научиться выполнять
проектировочный и проверочный расчет
передачи

3.

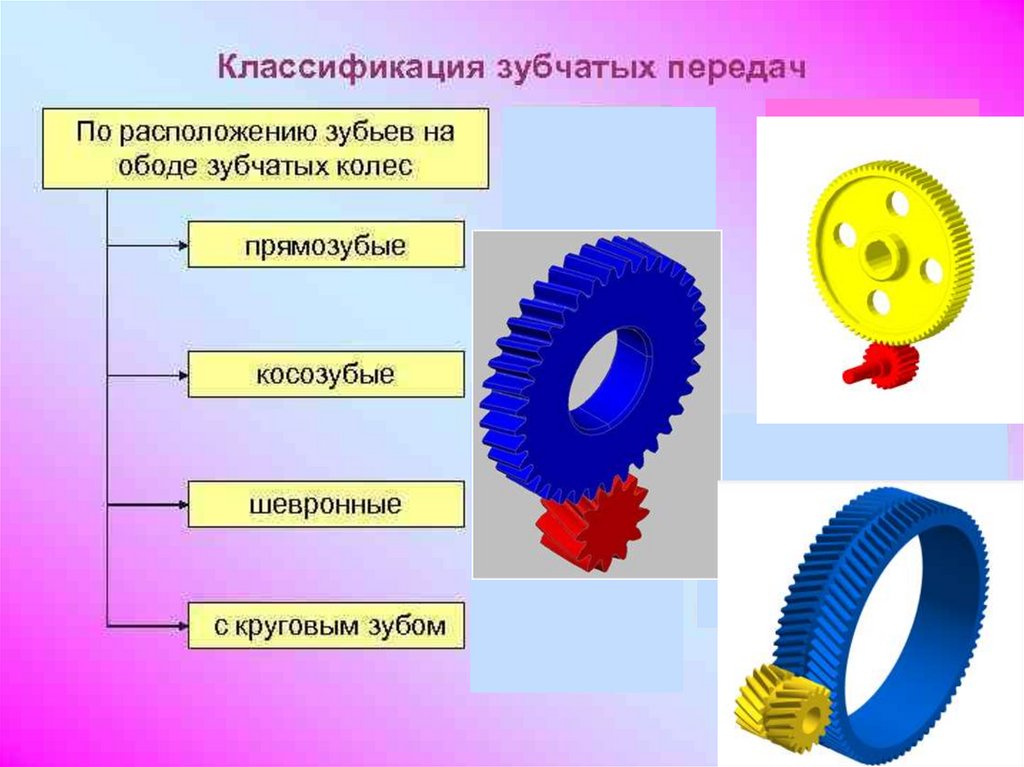
1. Классификация цилиндрических зубчатых
передач (ЦЗП).
2. Достоинства и недостатки ЦЗП. Область
применения.
3. Геометрический расчет прямозубой ЦЗП.
4. Геометрический расчет косозубой ЦЗП.
5. Расчет ЦЗП на контактную прочность.
6.Расчет ЦЗП на прочность при изгибе.
7.Особенности расчета косозубых и шевронных
передач.

4.

1. КЛАССИФИКАЦИЯ
ЦИЛИНДРИЧЕСКИХ
ЗУБЧАТЫХ ПЕРЕДАЧ.

5.

6.

7.

8.

9.

10.

КОНСТРУКТИВНЫЕ ЭЛЕМЕНТЫ
ЦИЛИНДРИЧЕСКОГО ЗУБЧАТОГО КОЛЕСА

11.

2. ДОСТОИНСТВА И
НЕДОСТАТКИ ЦЗП. ОБЛАСТЬ
ПРИМЕНЕНИЯ.

12.

13.

14.

15.

16.

17.

18.

19.

20.

3. ГЕОМЕТРИЧЕСКИЙ РАСЧЕТ
ЦИЛИНДРИЧЕСКОЙ
ПРЯМОЗУБОЙ ПЕРЕДАЧИ.

21.

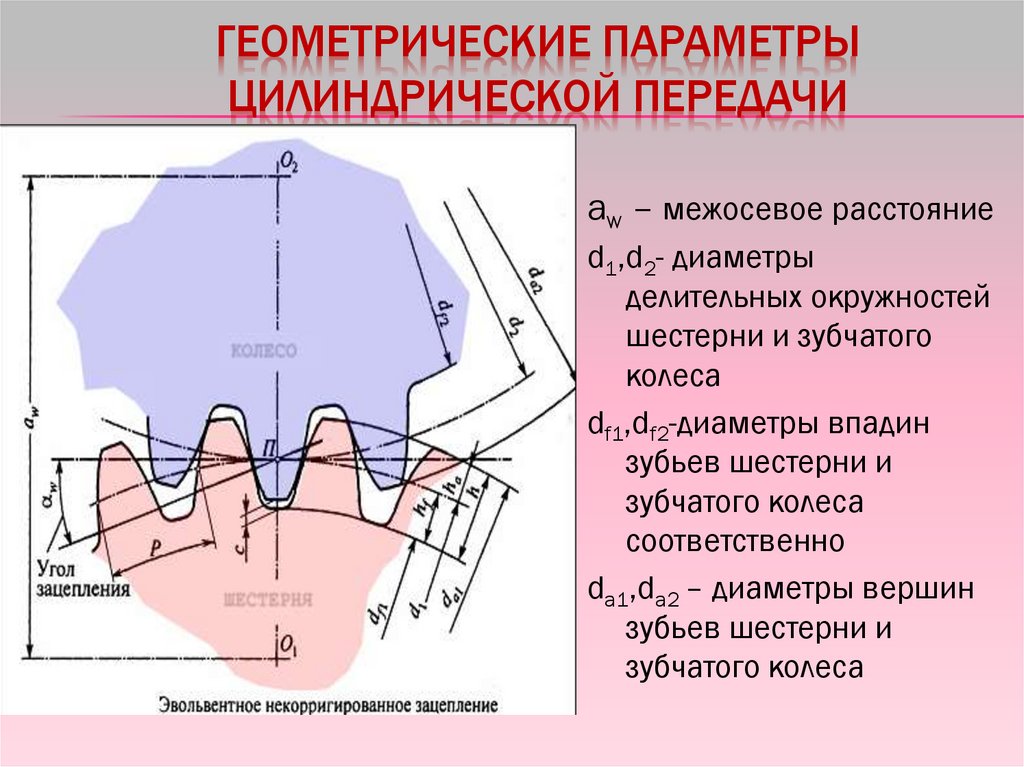
ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ
ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
aw – межосевое расстояние
d1,d2- диаметры
делительных окружностей
шестерни и зубчатого
колеса
df1,df2-диаметры впадин
зубьев шестерни и
зубчатого колеса
соответственно
dа1,dа2 – диаметры вершин
зубьев шестерни и
зубчатого колеса

22.

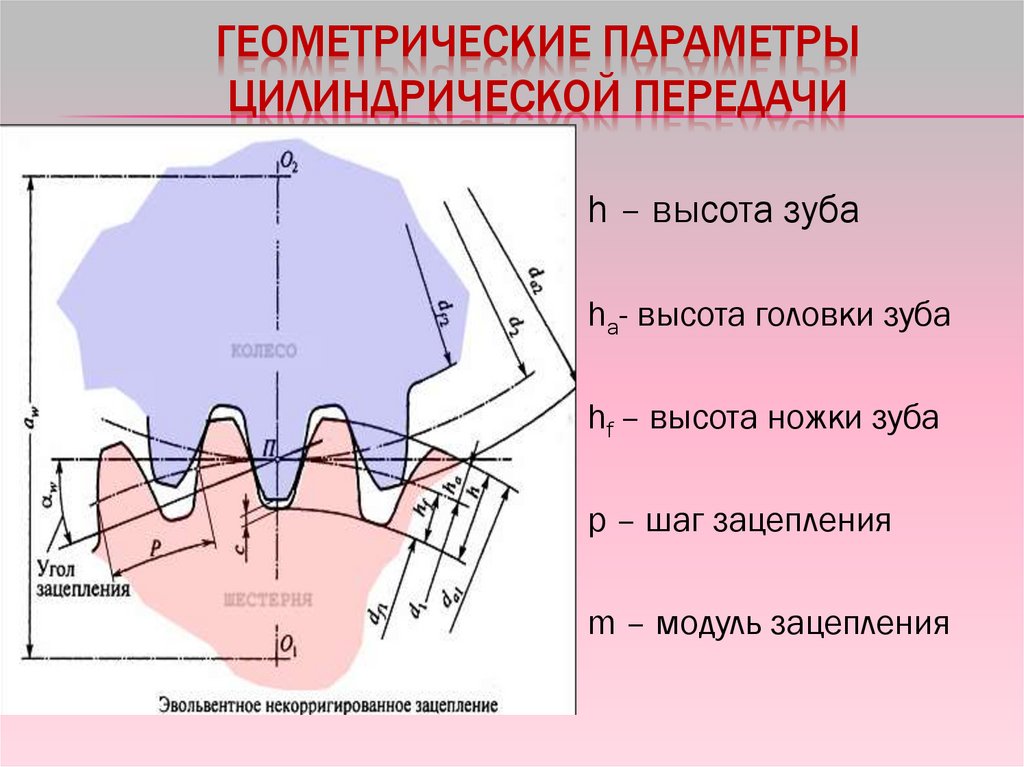
ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ
ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
h – высота зуба
ha- высота головки зуба
hf – высота ножки зуба
р – шаг зацепления
m – модуль зацепления

23.

24.

*- если поставлено условие придерживаться
стандартных значений u, то следует округлить
вычисленное значение до величины по ГОСТ 2185-66
1-ый ряд: 1; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3;
8,0; 10,0;
2-ой ряд: 1,12; 1,4; 1,8; 2,24; 2,8; 3,55; 4,5; 5,6;
7,1; 9,0; 11,2;
Первый ряд стоит предпочитать второму.
** - полученное значение модуля выравнивают по ГОСТ
9563-60
1-ый ряд: 1; 1,25; 2; 2,5; 3; 4; 6; 8; 10; 12; 16; 20;
2-ой ряд: 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 7; 9; 11;
14; 18; 22.
Первый ряд следует предпочитать второму.

25.

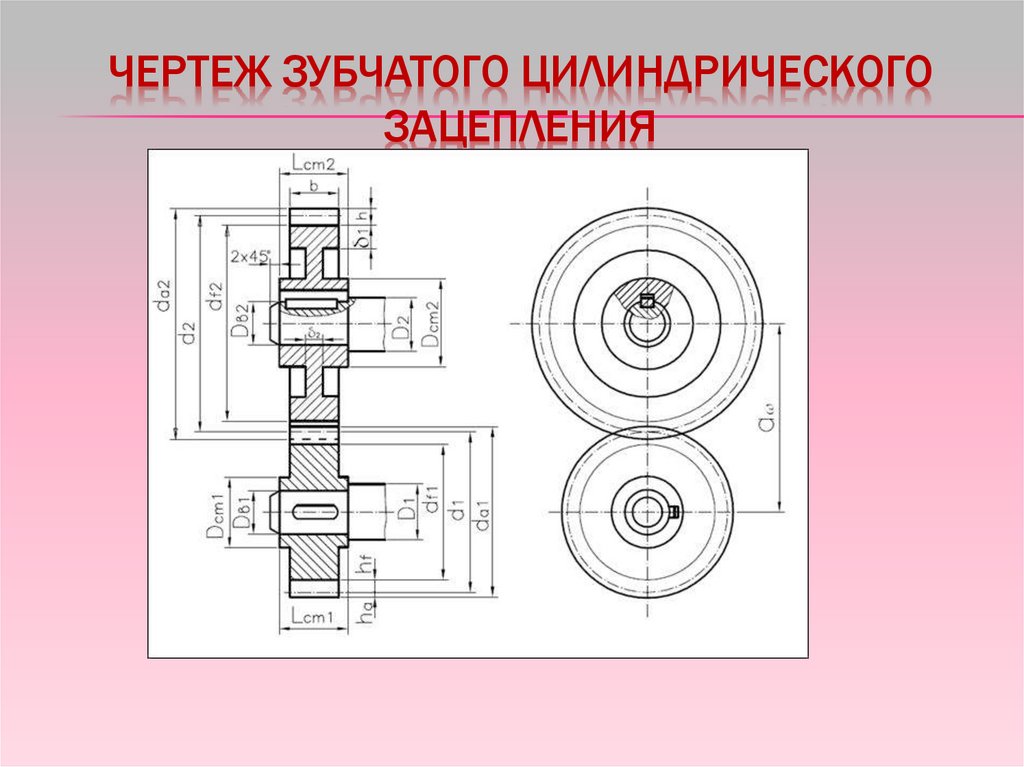
ЧЕРТЕЖ ЗУБЧАТОГО ЦИЛИНДРИЧЕСКОГО
ЗАЦЕПЛЕНИЯ

26.

4. ГЕОМЕТРИЧЕСКИЙ РАСЧЕТ
ЦИЛИНДРИЧЕСКОЙ
КОСОЗУБОЙ ПЕРЕДАЧИ.

27.

Геометрические параметры цилиндрической
косозубой и шевронной передач с
эвольвентным профилем зуба рассчитают по
формулам, приведенным в таблице ниже.
По торцовому модулю mt рассчитывают
делительные (начальные) диаметры, а
по mп — все остальные размеры зубчатых
колес.

28.

Параметры
Обозначение
Расчетная формула
Передаточное число
u
u= z2/z1
Угол наклона линии зуба
β
β=arccos(zΣ·mn/2·aw)
Диаметры
делительных
окружностей шестерни и колеса
d1
d1=mn·z1/cosβ
d2
d2= mn·z2/cosβ
aw
aw=(d1+d2)/2
Диаметры окружностей вершин
зубьев шестерни и колеса
da1
da1= d1+2mn
da2
da2= d2+2mn
Диаметры окружностей впадин
шестерни и колеса
df1
df1=d1-2.5mn
Ширина
колеса
b2
Уточненное
расстояние
венцов
межосевое
шестерни
и
df2
b1
df2=d2-2.5mn
b2= Ψba· aw
b1=b2+4
Элементы зуба:
Высота зуба
Высота головки
Высота ножки
Торцовый модуль
Шаг зацепления:
Нормальный
h
ha
hf
mt
P
Pn
h=2.25mn
ha=mn
hf=1.25mn
mt=mn/cosβ
P=π·m
P=π·mn
Торцовый
Pt
P=π·mt

29.

5.РАСЧЕТ ЦИЛИНДРИЧЕСКОЙ
ЗУБЧАТОЙ ПЕРЕДАЧИ НА
КОНТАКТНУЮ ПРОЧНОСТЬ .

30.

Контактная прочность зубьев является
основным критерием работоспособности
большинства зубчатых передач.
Исследованиями установлено, что
наименьшей контактной выносливостью
обладает околополюсная зона рабочих
поверхностей зубьев.
Поэтому расчет зубьев на контактную
прочность принято выполнять при контакте
зубьев в полюсе зацепления.
Цель расчета- предупреждение усталостного
выкрашивания рабочих поверхностных слоев
зубьев в течение заданного срока.

31.

УСЛОВИЕ КОНТАКТНОЙ ВЫНОСЛИВОСТИ
ИМЕЕТ ВИД
Максимальное
GH≤[GH]
контактное
напряжение в
зоне контакта не
должно
превышать
величины
допускаемого
контактного
напряжения.

32.

ОСНОВНЫМ ГЕОМЕТРИЧЕСКИМ ПАРАМЕТРОМ, КОТОРЫЙ
СЧИТАЕТСЯ ПЕРВЫМ ПРИ ПРОЕКТИРОВОЧНОМ РАСЧЕТЕ
ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ ЯВЛЯЕТСЯ
МЕЖОСЕВОЕ РАССТОЯНИЕ
aw k a u 1 3
T2 10 K H
3
H u ba
2
2
Ка- для прямозубых передач Ка= 49,5; для косозубых и
шевронных Ка = 43,0
[GH] – допускаемое контактное напряжение, Н/мм2 или
МПа
u – передаточное число передачи;
Т2 – вращающий момент на тихоходном валу, Нмм
KH=KHἀ·KHβ·KHv–коэффициент нагрузки

33.

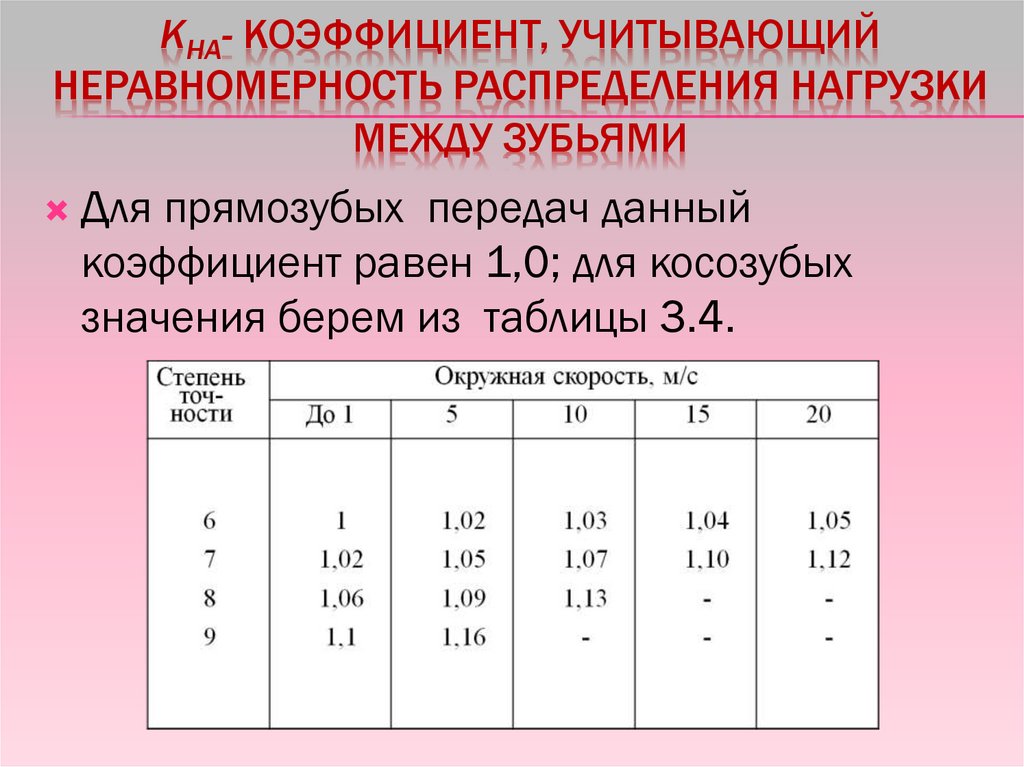
KHΑ- КОЭФФИЦИЕНТ, УЧИТЫВАЮЩИЙ
НЕРАВНОМЕРНОСТЬ РАСПРЕДЕЛЕНИЯ НАГРУЗКИ
МЕЖДУ ЗУБЬЯМИ
Для прямозубых передач данный
коэффициент равен 1,0; для косозубых
значения берем из таблицы 3.4.

34.

KHΒ- КОЭФФИЦИЕНТ, УЧИТЫВАЮЩИЙ
НЕРАВНОМЕРНОСТЬ НАГРУЗКИ ПО ШИРИНЕ
ВЕНЦА
для определения этого коэффициента
необходимо рассчитать значение Ψbd=b/d1, а
затем воспользоваться следующей таблицей.
При постоянной нагрузке KHβ=1.

35.

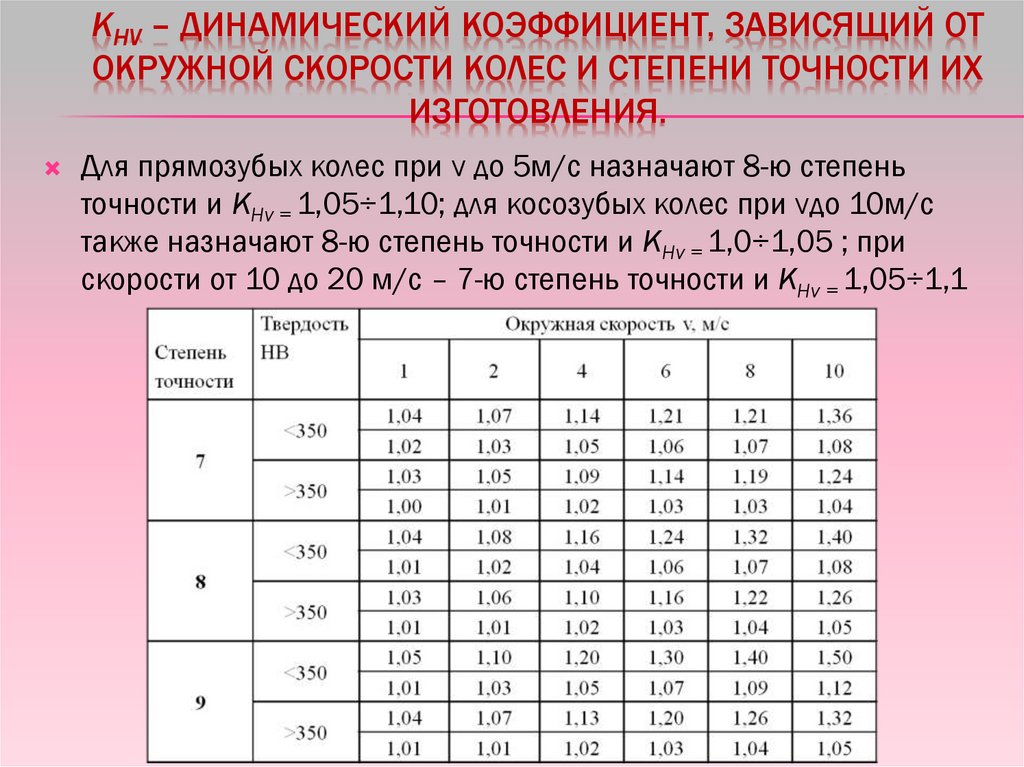
KHV – ДИНАМИЧЕСКИЙ КОЭФФИЦИЕНТ, ЗАВИСЯЩИЙ ОТ
ОКРУЖНОЙ СКОРОСТИ КОЛЕС И СТЕПЕНИ ТОЧНОСТИ ИХ
ИЗГОТОВЛЕНИЯ.
Для прямозубых колес при v до 5м/с назначают 8-ю степень
точности и KHv = 1,05÷1,10; для косозубых колес при vдо 10м/с
также назначают 8-ю степень точности и KHv = 1,0÷1,05 ; при
скорости от 10 до 20 м/с – 7-ю степень точности и KHv = 1,05÷1,1

36.

ПОСЛЕ ОПРЕДЕЛЕНИЯ МЕЖОСЕВОГО
РАССТОЯНИЯ МОЖНО ОПРЕДЕЛИТЬ
КОНТАКТНОЕ НАПРЯЖЕНИЕ.
Для прямозубых передач
H
310
a
w
T2 10 3 K H (u 1) 3
b2 u 2
Для косозубых передач
H
270
a
w
T2 10 3 K H (u 1) 3
b2 u 2

37.

6.РАСЧЕТ ЦИЛИНДРИЧЕСКОЙ
ЗУБЧАТОЙ ПЕРЕДАЧИ НА
ПРОЧНОСТЬ ПРИ ИЗГИБЕ .

38.

Силы в зацеплении прямозубых цилиндрических
зубчатых передач
,
Окружная сила
2 T1 2 T2
Ft Fn Cos w
d1
d2
Радиальная сила
Fr Ft tg w

39.

Поломка зубьев связана с напряжениями
изгиба, вследствие усталости материала от
длительно действующих нагрузок.
Расчет на изгиб сводится к проверке условия:
σF≤[σF]

40.

ПРИ ВЫВОДЕ РАСЧЁТНОЙ ФОРМУЛЫ ДЛЯ
ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ ИЗГИБА
ПРИНИМАЮТ СЛЕДУЮЩИЕ ДОПУЩЕНИЯ:
1) вся
нагрузка зацепления
передается одной парой
зубьев, которая приложена
к вершине зуба и
направлена по нормали к
его профилю (сила трения
не учитываются);
2) зуб рассматривают как
консольную балку
прямоугольного сечения, что
позволяет рассчитывать его
методами сопротивления
материалов. Фактически зуб
представляет собой балку с
изменяющейся формой. Это
учитывается введением в
расчётные формулы
теоретического
коэффициента
концентрации напряжений
Кт.

41.

ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ ПРИ ПРОВЕРКЕ
ЗУБЬЕВ ПО НАПРЯЖЕНИЯМ ИЗГИБА ОПРЕДЕЛЯЮТ
ПО ФОРМУЛЕ:
[ F ]
F lim b
[S F ]
G0Flimb- предел выносливости (сведения о нем приведены в
таблице 3.9 [1])
[SF]- коэффициент безопасности, определяется как произведение
двух коэффициентов
[SF]= [SF]´· [SF]´´
[SF]´ - коэффициент, учитывающий нестабильность свойств
материала зубчатых колес (его значения приведены в таблице 3,9
[1])
[SF]´´- коэффициент, учитывающий способ получения заготовки
зубчатого колеса ( для поковок и штамповок – 1,0; для проката1,15; для литых заготовок- 1,3).

42.

ТОГДА ПОСЛЕ ПОДСТАНОВКИ В ИСХОДНУЮ
ФОРМУЛУ, ФОРМУЛА ПРОВЕРОЧНОГО РАСЧЁТА
ПРЯМОЗУБЫХ ПЕРЕДАЧ:
Ft K F YF
F
[ F ]
b m
где σF и [σF] - расчётное и допускаемое
напряжения изгиба, Н/мм2.
Ft – окружная сила, H,
b и m – ширина и модуль зубчатого колеса или
шестерни, мм,
YF – коэффициент формы зуба – величина
безразмерная, зависящая от числа зубьев z или
zv и коэффициента смещения х.

43.

KF -КОЭФФИЦИЕНТ НАГРУЗКИ ПРИ РАСЧЕТЕ
НА ИЗГИБ
KF=KFα ∙ KFβ ∙ KFV
KFα
коэффициент
нагрузки,
учитывающий
распределение нагрузки между зубьями (для
прямозубых передач KFα =1 );
KFβ
коэффициент
нагрузки,
учитывающий
неравномерность распределения нагрузки по ширине
зубчатого венца (по длине контактных линий),
значения в таблице 2.7.;
KFV
коэффициент
нагрузки,
учитывающий
дополнительные динамические нагрузки, значения в
таблице 2.8.

44.

7. ОСОБЕННОСТИ РАСЧЕТА
КОСОЗУБЫХ И ШЕВРОННЫХ
ПЕРЕДАЧ.

45.

Силы в зацеплении косозубых цилиндрических
зубчатых передач
Окружная сила
2 T1 2 T2
Ft Fn Cos w
d1
d2
tg
Fr Ft
радиальная сила
Cos
осевая сила
Fa Ft tg

46.

НЕСУЩАЯ СПОСОБНОСТЬ КОСОЗУБЫХ И ШЕВРОННЫХ
КОЛЕС ВЫШЕ, ЧЕМ ПРЯМОЗУБЫХ. ЭТА ОСОБЕННОСТЬ
ОТРАЖЕНА В ФОРМУЛЕ ДЛЯ РАСЧЕТА КОНТАКТНЫХ
НАПРЯЖЕНИЙ НА ИЗГИБ.
F
Ft K F YF Y K F
b m
Ft – окружная сила, H,
b и m – ширина и модуль зубчатого колеса или шестерни, мм,
YF – коэффициент формы зуба (коэффициент YF имеет то же значение, что и для
прямозубых колес, с той, однако, разницей, что его следует выбирать по
эквивалентному числу зубьев);
KF-коэффициент нагрузки при расчете на изгиб, который определяется по формуле
KF= KFβ·KFV
KFβ - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки
по ширине зубчатого венца (по длине контактных линий), определяется по таблице 3.7
[1];
KFV - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки,
определяется по таблице 3.8 [1].
Yβ – коэффициент компенсации погрешности, возникающей из- за применения той же
расчетной схемы зуба, что и в случае прямых зубьев
KFα - коэффициент нагрузки, учитывающий распределение нагрузки между зубьями

47.

Yβ – коэффициент компенсации погрешности, возникающей
из- за применения той же расчетной схемы зуба, что и в
случае прямых зубьев, который определяем по формуле
Y 1
140
KFα - коэффициент нагрузки, учитывающий распределение
нагрузки между зубьями, который определяем по формуле :
K F
4 ( 1)( n 5)
4
где ɛα- коэффициент торцового перекрытия ( при учебном
проектировании можно принимать ɛα = 1,5);
n- степень точности зубчатых колес (n= 8)

48.

КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. К каким видам передач относятся цилиндрические
в зависимости от взаимного расположения валов?
2.Какие существуют виды цилиндрических зубчатых
передач в зависимости от расположения зубьев
относительно обода зубчатого колеса?
3. Какие Вы знаете профили зубьев зубчатых колес?
4.Какой профиль зубьев зубчатых колес считается
самым распространенным в машиностроении?
5.Высокий КПД – это достоинство или недостаток
цилиндрических зубчатых передач?
6.Где в современном автомобилестроении используют
цилиндрические зубчатые передачи?

49.

Спасибо
за
внимание!