Similar presentations:
Перестановки. Лекция 23
1.
ПерестановкиЛекция 23
2.
План лекции• Перестановки и инверсии
• Восстановление перестановки по таблице инверсий
• Построение следующей таблицы инверсии
• Построение следующей перестановки
• Таблица инверсий
• Лексикографический порядок (Дейкстра)
• Время работы алгоритма Дейкстры в среднем
3.
Перестановки• Перестановкой порядка N
называется взаимнооднозначное отображение
множества из N элементов в себя
• Рассматриваем только
перестановки натуральных чисел
• a1, …, aN – запись перестановки
такой, что (1) = a1, …, (N) = aN
• Все возможные перестановки
множества { 1, 2, 3 } :
• 1, 2, 3
• 1, 3, 2
• 2, 1, 3
• 2, 3, 1
• 3, 1, 2
• 3, 2, 1
4.
Перестановки• Перестановкой порядка N
называется взаимнооднозначное отображение
множества из N элементов в себя
• Рассматриваем только
перестановки натуральных чисел
• a1, …, aN – запись перестановки
такой, что (1) = a1, …, (N) = aN
• Все возможные перестановки
множества { 1, 2, 3 } :
• 1, 2, 3
• 1, 3, 2
• 2, 1, 3
• 2, 3, 1
• 3, 1, 2
• 3, 2, 1
5.
Перестановки• Перестановкой порядка N
называется взаимнооднозначное отображение
множества из N элементов в себя
• Рассматриваем только
перестановки натуральных чисел
• a1, …, aN – запись перестановки
такой, что (1) = a1, …, (N) = aN
• Все возможные перестановки
множества { 1, 2, 3 } :
• 1, 2, 3
• 1, 3, 2
• 2, 1, 3
• 2, 3, 1
• 3, 1, 2
• 3, 2, 1
6.
Перестановки• Перестановкой порядка N
называется взаимнооднозначное отображение
множества из N элементов в себя
• Рассматриваем только
перестановки натуральных чисел
• a1, …, aN – запись перестановки
такой, что (1) = a1, …, (N) = aN
• Все возможные перестановки
множества { 1, 2, 3 } :
• 1, 2, 3
• 1, 3, 2
• 2, 1, 3
• 2, 3, 1
• 3, 1, 2
• 3, 2, 1
7.
Перестановки• Перестановкой порядка N
называется взаимнооднозначное отображение
множества из N элементов в себя
• Рассматриваем только
перестановки натуральных чисел
• a1, …, aN – запись перестановки
такой, что (1) = a1, …, (N) = aN
• Все возможные перестановки
множества { 1, 2, 3 } :
• 1, 2, 3
• 1, 3, 2
• 2, 1, 3
• 2, 3, 1
• 3, 1, 2
• 3, 2, 1
8.
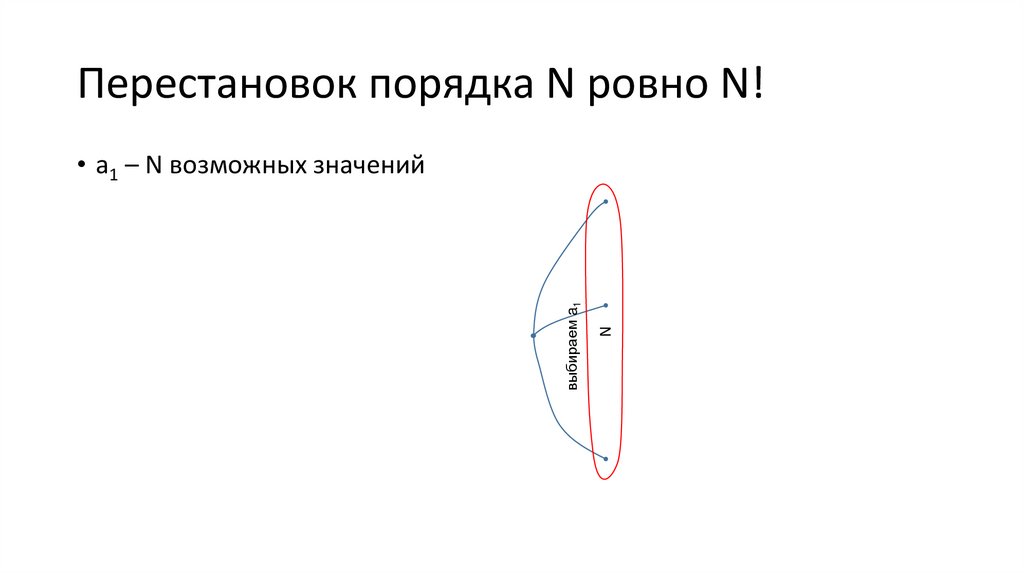
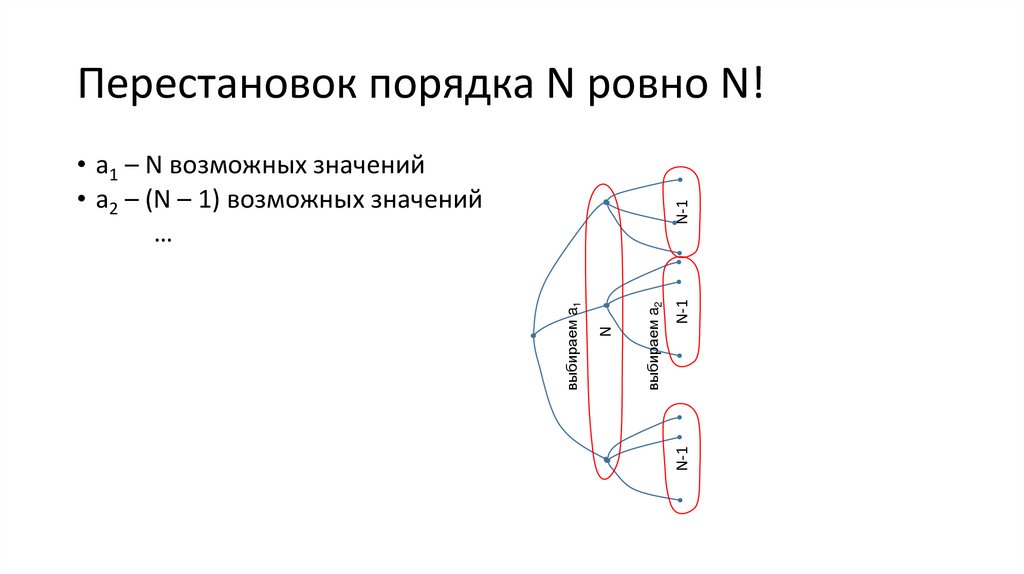
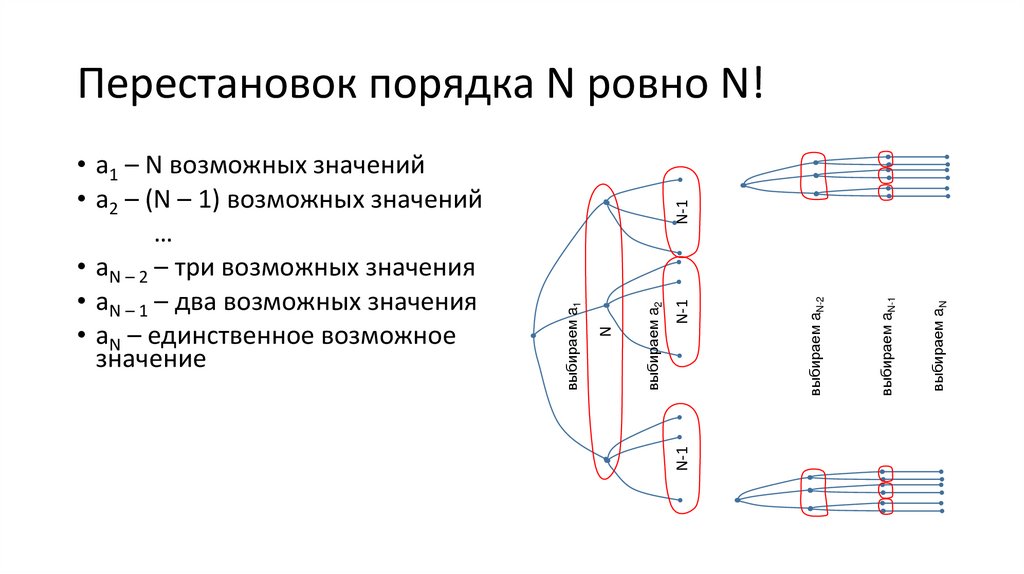
Перестановок порядка N ровно N!• a1 – N возможных значений
• a2 – (N – 1) возможных значений
…
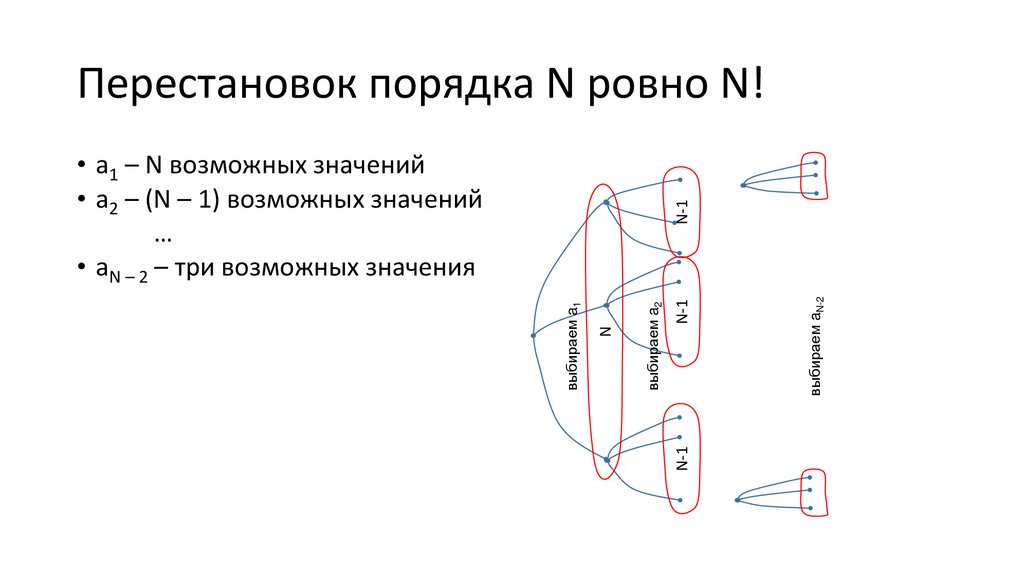
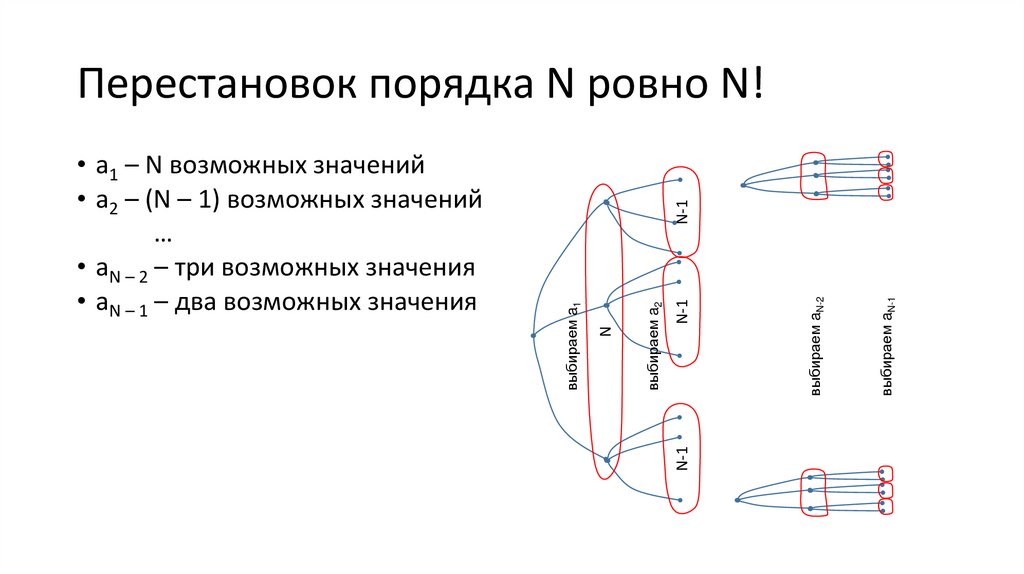
• aN – 2 – три возможных значения
• aN – 1 – два возможных значения
• aN – единственное возможное
значение
• Перестановок a1, …, aN – ровно
N∙(N −1)∙(N − 2)∙ ... ∙1 возможных
значений
9.
• Перестановок a1, …, aN – ровноN∙(N −1)∙(N − 2)∙ ... ∙1 возможных
значений
N
• a1 – N возможных значений
• a2 – (N – 1) возможных значений
…
• aN – 2 – три возможных значения
• aN – 1 – два возможных значения
• aN – единственное возможное
значение
выбираем a1
Перестановок порядка N ровно N!
10.
выбираем a2N
N-1
N-1
• Перестановок a1, …, aN – ровно
N∙(N −1)∙(N − 2)∙ ... ∙1 возможных
значений
выбираем a1
• a1 – N возможных значений
• a2 – (N – 1) возможных значений
…
• aN – 2 – три возможных значения
• aN – 1 – два возможных значения
• aN – единственное возможное
значение
N-1
Перестановок порядка N ровно N!
11.
выбираем aN-2выбираем a2
N
N-1
N-1
• Перестановок a1, …, aN – ровно
N∙(N −1)∙(N − 2)∙ ... ∙1 возможных
значений
выбираем a1
• a1 – N возможных значений
• a2 – (N – 1) возможных значений
…
• aN – 2 – три возможных значения
• aN – 1 – два возможных значения
• aN – единственное возможное
значение
N-1
Перестановок порядка N ровно N!
12.
выбираем aN-1выбираем aN-2
выбираем a2
N
N-1
N-1
• Перестановок a1, …, aN – ровно
N∙(N −1)∙(N − 2)∙ ... ∙1 возможных
значений
выбираем a1
• a1 – N возможных значений
• a2 – (N – 1) возможных значений
…
• aN – 2 – три возможных значения
• aN – 1 – два возможных значения
• aN – единственное возможное
значение
N-1
Перестановок порядка N ровно N!
13.
выбираем aNвыбираем aN-1
выбираем aN-2
выбираем a2
N
N-1
N-1
• Перестановок a1, …, aN – ровно
N∙(N −1)∙(N − 2)∙ ... ∙1 возможных
значений
выбираем a1
• a1 – N возможных значений
• a2 – (N – 1) возможных значений
…
• aN – 2 – три возможных значения
• aN – 1 – два возможных значения
• aN – единственное возможное
значение
N-1
Перестановок порядка N ровно N!
14.
выбираем aNвыбираем aN-1
выбираем aN-2
выбираем a2
N
N-1
N-1
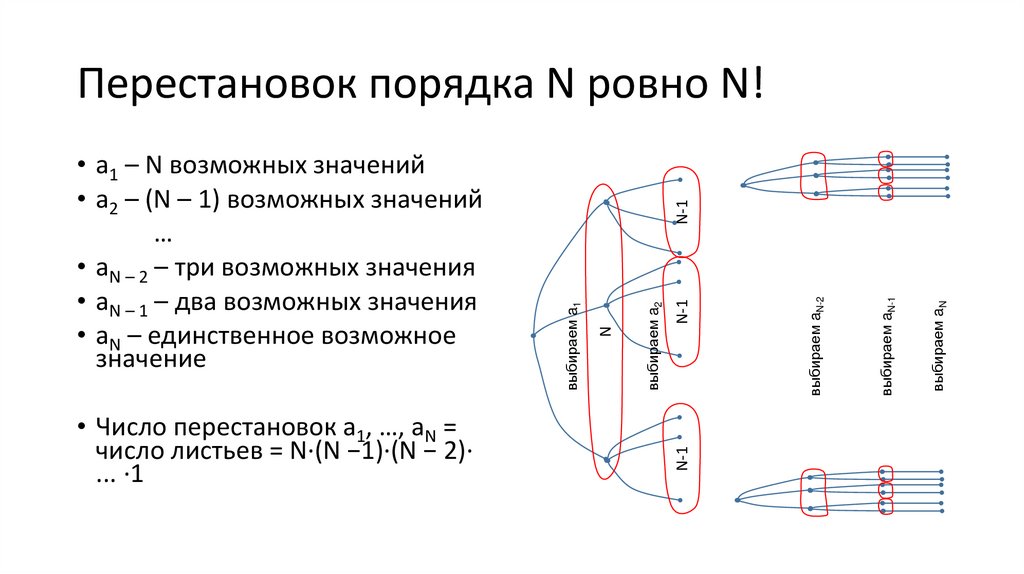
• Число перестановок a1, …, aN =
число листьев = N∙(N −1)∙(N − 2)∙
... ∙1
выбираем a1
• a1 – N возможных значений
• a2 – (N – 1) возможных значений
…
• aN – 2 – три возможных значения
• aN – 1 – два возможных значения
• aN – единственное возможное
значение
N-1
Перестановок порядка N ровно N!
15.
Инверсии• Пара ( i, j ) называется
инверсией (инверсионной
парой) перестановки а1, а2, ...,
aN , если аi > аj и i < j
• Инверсия — это пара позиций,
нарушающих упорядоченность
перестановки
• Инверсионные пары
перестановки 4, 1, 3, 2
• (1, 2)
• (1, 3)
• (1, 4)
• (3, 4)
• Проверьте по определению
16.
Инверсии• Пара ( i, j ) называется
инверсией (инверсионной
парой) перестановки а1, а2, ...,
aN , если аi > аj и i < j
• Инверсия — это пара позиций,
нарушающих упорядоченность
перестановки
• Инверсионные пары
перестановки 4, 1, 3, 2
• (1, 2)
• (1, 3)
• (1, 4)
• (3, 4)
• Проверьте по определению
17.
Инверсии• Пара ( i, j ) называется
инверсией (инверсионной
парой) перестановки а1, а2, ...,
aN , если аi > аj и i < j
• Инверсия — это пара позиций,
нарушающих упорядоченность
перестановки
• Инверсионные пары
перестановки 4, 1, 3, 2
• (1, 2)
• (1, 3)
• (1, 4)
• (3, 4)
• Проверьте по определению
18.
Инверсии• Пара ( i, j ) называется
инверсией (инверсионной
парой) перестановки а1, а2, ...,
aN , если аi > аj и i < j
• Инверсия — это пара позиций,
нарушающих упорядоченность
перестановки
• Инверсионные пары
перестановки 4, 1, 3, 2
• (1, 2)
• (1, 3)
• (1, 4)
• (3, 4)
• Проверьте по определению
19.
Инверсии• Пара ( i, j ) называется
инверсией (инверсионной
парой) перестановки а1, а2, ...,
aN , если аi > аj и i < j
• Инверсия — это пара позиций,
нарушающих упорядоченность
перестановки
• Инверсионные пары
перестановки 4, 1, 3, 2
• (1, 2)
• (1, 3)
• (1, 4)
• (3, 4)
• Проверьте по определению
20.
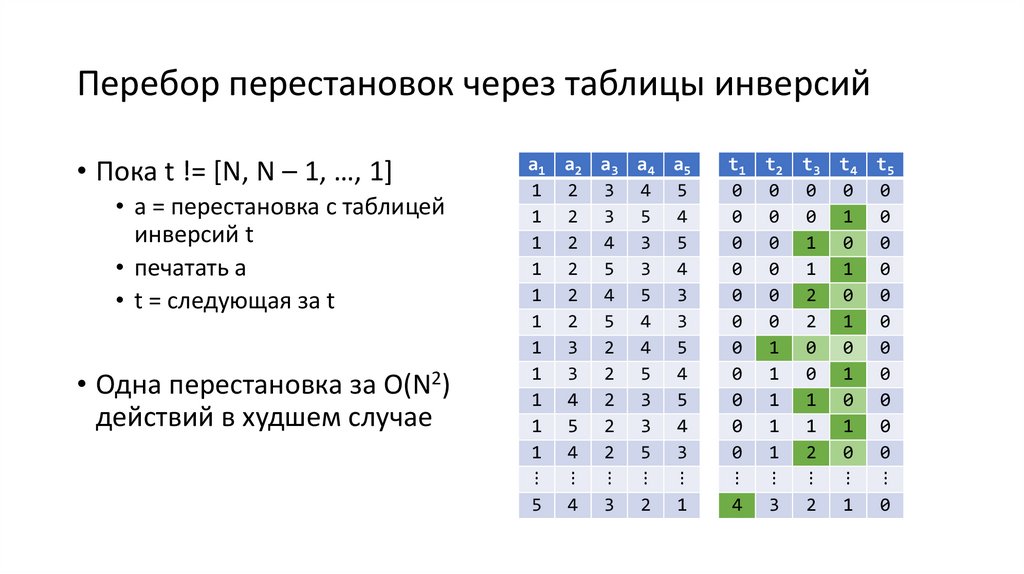
Число инверсий и сортировка21.
Число инверсий и сортировка• Если у перестановки нет инверсий, то это 1, 2, 3, ... , N
• Если у перестановки k инверсий, то для её сортировки достаточно
k обменов
• Пусть (i, j) – инверсия перестановки a; пусть b = a + обмен ai <-> aj
22.
Число инверсий и сортировка• Если у перестановки нет инверсий, то это 1, 2, 3, ... , N
• Если у перестановки k инверсий, то для её сортировки достаточно
k обменов
• Пусть (i, j) – инверсия перестановки a; пусть b = a + обмен ai <-> aj
23.
Число инверсий и сортировка• Если у перестановки нет инверсий, то это 1, 2, 3, ... , N
• Если у перестановки k инверсий, то для её сортировки достаточно
k обменов
• Пусть (i, j) – инверсия перестановки a; пусть b = a + обмен ai <-> aj
24.
Число инверсий и сортировка• Если у перестановки нет инверсий, то это 1, 2, 3, ... , N
• Если у перестановки k инверсий, то для её сортировки достаточно
k обменов
• Пусть (i, j) – инверсия перестановки a; пусть b = a + обмен ai <-> aj
число инверсий (x, y), где x < i
одинаковое у a и b
• множество инверсий
меняется, т.к. меняется
порядок значений by
• число инверсий
сохраняется
i
число инверсий (x, y), где i ≤ x ≤ j
j число инверсий (x, y), где j < x
у b меньше, чем у a
• нет инверсии (i, j) и,
возможно, каких-то еще, т.к. bj
> aj и b i < ai
одинаковое у a и b
• совпадает не только число,
но и само множество таких
инверсий
25.
Число инверсий и сортировка• Если у перестановки нет инверсий, то это 1, 2, 3, ... , N
• Если у перестановки k инверсий, то для её сортировки достаточно
k обменов
• Пусть (i, j) – инверсия перестановки a; пусть b = a + обмен ai <-> aj
число инверсий (x, y), где x < i
одинаковое у a и b
• множество инверсий
меняется, т.к. меняется
порядок значений by
• число инверсий
сохраняется
i
число инверсий (x, y), где i ≤ x ≤ j
j число инверсий (x, y), где j < x
у b меньше, чем у a
• нет инверсии (i, j) и,
возможно, каких-то еще, т.к. bj
> aj и b i < ai
одинаковое у a и b
• совпадает не только число,
но и само множество таких
инверсий
26.
Число инверсий и сортировка• Если у перестановки нет инверсий, то это 1, 2, 3, ... , N
• Если у перестановки k инверсий, то для её сортировки достаточно
k обменов
• Пусть (i, j) – инверсия перестановки a; пусть b = a + обмен ai <-> aj
число инверсий (x, y), где x < i
одинаковое у a и b
• множество инверсий
меняется, т.к. меняется
порядок значений by
• число инверсий
сохраняется
i
число инверсий (x, y), где i ≤ x ≤ j
j число инверсий (x, y), где j < x
у b меньше, чем у a
• нет инверсии (i, j) и,
возможно, каких-то еще, т.к. bj
> aj и b i < ai
одинаковое у a и b
• совпадает не только число,
но и само множество таких
инверсий
27.
Таблица инверсий• Таблицей инверсий
перестановки a называется
последовательность чисел
t1, t2, …, tN, где tj = число
инверсий перестановки a
вида (x, j)
• a=
5,
9, , 8, 6 4 7
1
2,
• t = 2, 3, 6, 4, 0, 2, 2, 1, 0
, ,
,3
28.
Таблица инверсий• Таблицей инверсий
перестановки a называется
последовательность чисел
t1, t2, …, tN, где tj = число
инверсий перестановки a
вида (x, j)
• a=
5,
9, , 8, 6 4 7
1
2,
• t = 2, 3, 6, 4, 0, 2, 2, 1, 0
, ,
,3
29.
Таблица инверсий• Таблицей инверсий
перестановки a называется
последовательность чисел
t1, t2, …, tN, где ta[j] = число
инверсий перестановки a
вида (x, j)
• a=
5,
9, , 8, 6 4 7
1
2,
• t = 2, 3, 6, 4, 0, 2, 2, 1, 0
, ,
,3
30.
Свойства таблицы инверсий• Последовательность t1, t2, …, tN является таблицей инверсий
некоторой перестановки тогда и только тогда, когда для всех i = 1,
…, N выполняется 0 ≤ ti ≤ N – i
• Таблица инверсий определяет перестановку однозначно
31.
Свойства таблицы инверсий• Последовательность t1, t2, …, tN является таблицей инверсий
некоторой перестановки тогда и только тогда, когда для всех i = 1,
…, N выполняется 0 ≤ ti ≤ N – i
• Таблица инверсий определяет перестановку однозначно
32.
Свойства таблицы инверсий• Последовательность t1, t2, …, tN является таблицей инверсий
некоторой перестановки тогда и только тогда, когда для всех i = 1,
…, N выполняется 0 ≤ ti ≤ N – i
• Таблица инверсий определяет перестановку однозначно
33.
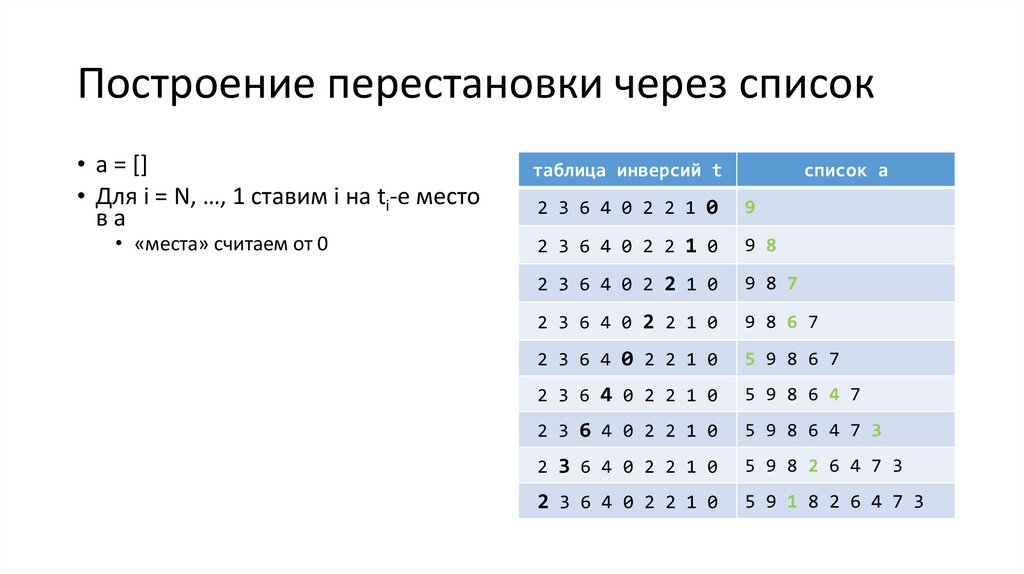
Построение перестановки через список• a = []
• Для i = N, …, 1 ставим i на ti-е место
вa
• «места» считаем от 0
• Таблица инверсий для a есть t:
• Пусть a = [x, y, z, …] после шага i
• Обозначим FrozenOrder(a) множество
всех перестановок, у которых x идёт
перед y, y – перед z и т.д.
• Таблица инверсий для любой
перестановки из FrozenOrder(a) имеет
вид ?, ?, …, ?, ti, ti+1, …, tN
34.
Построение перестановки через список• a = []
• Для i = N, …, 1 ставим i на ti-е место
вa
• «места» считаем от 0
• Таблица инверсий для a есть t:
• Пусть a = [x, y, z, …] после шага i
• Обозначим FrozenOrder(a) множество
всех перестановок, у которых x идёт
перед y, y – перед z и т.д.
• Таблица инверсий для любой
перестановки из FrozenOrder(a) имеет
вид ?, ?, …, ?, ti, ti+1, …, tN
35.
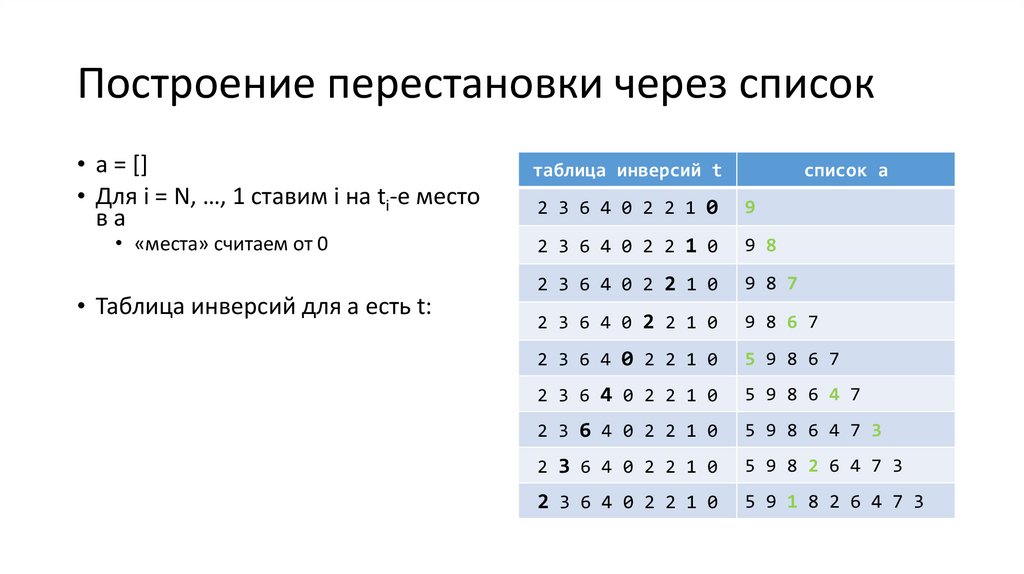
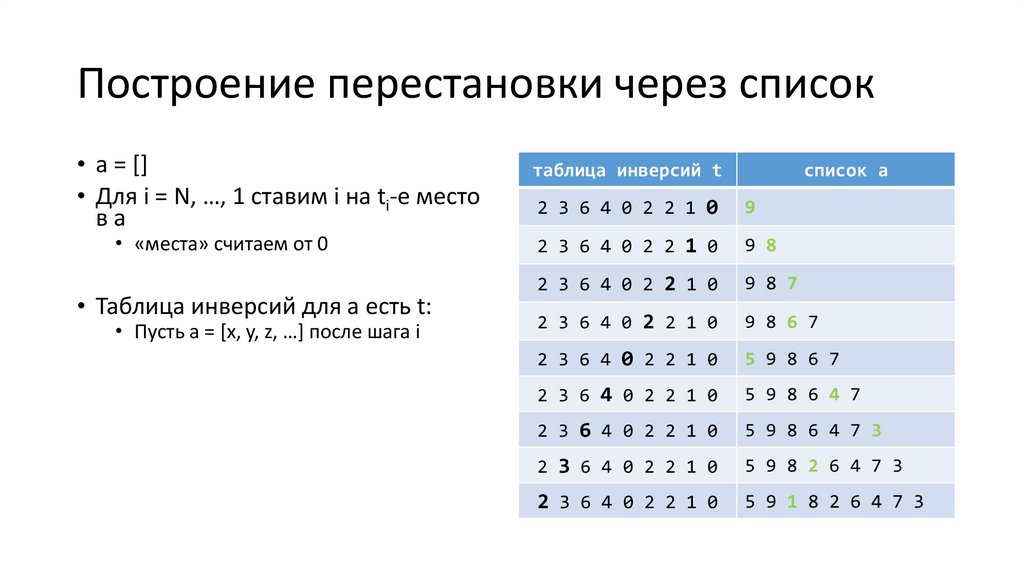
Построение перестановки через список• a = []
• Для i = N, …, 1 ставим i на ti-е место
вa
• «места» считаем от 0
• Таблица инверсий для a есть t:
• Пусть a = [x, y, z, …] после шага i
• Обозначим FrozenOrder(a) множество
всех перестановок, у которых x идёт
перед y, y – перед z и т.д.
• Таблица инверсий для любой
перестановки из FrozenOrder(a) имеет
вид ?, ?, …, ?, ti, ti+1, …, tN
таблица инверсий t
список а
2 3 6 4 0 2 2 1 0
9
2 3 6 4 0 2 2 1 0
9 8
2 3 6 4 0 2 2 1 0
9 8 7
2 3 6 4 0 2 2 1 0
9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
36.
Построение перестановки через список• a = []
• Для i = N, …, 1 ставим i на ti-е место
вa
• «места» считаем от 0
• Таблица инверсий для a есть t:
• Пусть a = [x, y, z, …] после шага i
• Обозначим FrozenOrder(a) множество
всех перестановок, у которых x идёт
перед y, y – перед z и т.д.
• Таблица инверсий для любой
перестановки из FrozenOrder(a) имеет
вид ?, ?, …, ?, ti, ti+1, …, tN
таблица инверсий t
список а
2 3 6 4 0 2 2 1 0
9
2 3 6 4 0 2 2 1 0
9 8
2 3 6 4 0 2 2 1 0
9 8 7
2 3 6 4 0 2 2 1 0
9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
37.
Построение перестановки через список• a = []
• Для i = N, …, 1 ставим i на ti-е место
вa
• «места» считаем от 0
• Таблица инверсий для a есть t:
• Пусть a = [x, y, z, …] после шага i
• Обозначим FrozenOrder(a) множество
всех перестановок, у которых x идёт
перед y, y – перед z и т.д.
• Таблица инверсий для любой
перестановки из FrozenOrder(a) имеет
вид ?, ?, …, ?, ti, ti+1, …, tN
таблица инверсий t
список а
2 3 6 4 0 2 2 1 0
9
2 3 6 4 0 2 2 1 0
9 8
2 3 6 4 0 2 2 1 0
9 8 7
2 3 6 4 0 2 2 1 0
9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
38.
Построение перестановки через список• a = []
• Для i = N, …, 1 ставим i на ti-е место
вa
• «места» считаем от 0
• Таблица инверсий для a есть t:
• Пусть a = [x, y, z, …] после шага i
• Обозначим FrozenOrder(a) множество
всех перестановок, у которых x идёт
перед y, y – перед z и т.д.
• Таблица инверсий для любой
перестановки из FrozenOrder(a) имеет
вид ?, ?, …, ?, ti, ti+1, …, tN
таблица инверсий t
список а
2 3 6 4 0 2 2 1 0
9
2 3 6 4 0 2 2 1 0
9 8
2 3 6 4 0 2 2 1 0
9 8 7
2 3 6 4 0 2 2 1 0
9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
39.
Построение перестановки через список• a = []
• Для i = N, …, 1 ставим i на ti-е место
вa
• «места» считаем от 0
• Таблица инверсий для a есть t:
• Пусть a = [x, y, z, …] после шага i
• Обозначим FrozenOrder(a) множество
всех перестановок, у которых x идёт
перед y, y – перед z и т.д.
• Таблица инверсий для любой
перестановки из FrozenOrder(a) имеет
вид ?, ?, …, ?, ti, ti+1, …, tN
таблица инверсий t
список а
2 3 6 4 0 2 2 1 0
9
2 3 6 4 0 2 2 1 0
9 8
2 3 6 4 0 2 2 1 0
9 8 7
2 3 6 4 0 2 2 1 0
9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7
2 3 6 4 0 2 2 1 0
5 9 8 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
40.
Построение перестановки через списокTSequence RestorePermutation(const TSequence* inversions) {
TSequence permutation;
permutation = MakeEmptySequence();
for (int j = GetSize(inversions) - 1; j >= 0; --j) {
InsertAt(&permutation, GetElement(inversions, j), j);
}
return permutation;
}
41.
Тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence() {
TSequence sequence = {{0}, 0};
return sequence;
}
int GetSize(const TSequence* sequence) {
return sequence->Size;
}
int GetElement(const TSequence* sequence, int idx) {
assert(idx < sequence->Size);
return sequence->Data[idx];
}
int GetCapacity(const TSequence* sequence) {
return sizeof(sequence->Data)
/ sizeof(sequence->Data[0]);
}
void InsertAt(
TSequence* sequence, int idx, int value
) {
int size = GetSize(sequence);
assert(size + 1 < GetCapacity(sequence));
assert(idx <= size);
for (int i = size; i >= idx; --i) {
sequence->Data[i + 1] =
sequence->Data[i];
}
sequence->Data[idx] = value;
++sequence->Size;
}
42.
Тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence() {
TSequence sequence = {{0}, 0};
return sequence;
}
int GetSize(const TSequence* sequence) {
return sequence->Size;
}
int GetElement(const TSequence* sequence, int idx) {
assert(idx < sequence->Size);
return sequence->Data[idx];
}
int GetCapacity(const TSequence* sequence) {
return sizeof(sequence->Data)
/ sizeof(sequence->Data[0]);
}
void InsertAt(
TSequence* sequence, int idx, int value
) {
int size = GetSize(sequence);
assert(size + 1 < GetCapacity(sequence));
assert(idx <= size);
for (int i = size; i >= idx; --i) {
sequence->Data[i + 1] =
sequence->Data[i];
}
sequence->Data[idx] = value;
++sequence->Size;
}
43.
Тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence() {
TSequence sequence = {{0}, 0};
return sequence;
}
int GetSize(const TSequence* sequence) {
return sequence->Size;
}
int GetElement(const TSequence* sequence, int idx) {
assert(idx < sequence->Size);
return sequence->Data[idx];
}
int GetCapacity(const TSequence* sequence) {
return sizeof(sequence->Data)
/ sizeof(sequence->Data[0]);
}
void InsertAt(
TSequence* sequence, int idx, int value
) {
int size = GetSize(sequence);
assert(size + 1 < GetCapacity(sequence));
assert(idx <= size);
for (int i = size; i >= idx; --i) {
sequence->Data[i + 1] =
sequence->Data[i];
}
sequence->Data[idx] = value;
++sequence->Size;
}
44.
Тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence() {
TSequence sequence = {{0}, 0};
return sequence;
}
int GetSize(const TSequence* sequence) {
return sequence->Size;
}
int GetElement(const TSequence* sequence, int idx) {
assert(idx < sequence->Size);
return sequence->Data[idx];
}
int GetCapacity(const TSequence* sequence) {
return sizeof(sequence->Data)
/ sizeof(sequence->Data[0]);
}
void InsertAt(
TSequence* sequence, int idx, int value
) {
int size = GetSize(sequence);
assert(size + 1 < GetCapacity(sequence));
assert(idx <= size);
for (int i = size; i >= idx; --i) {
sequence->Data[i + 1] =
sequence->Data[i];
}
sequence->Data[idx] = value;
++sequence->Size;
}
45.
Тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence() {
TSequence sequence = {{0}, 0};
return sequence;
}
int GetSize(const TSequence* sequence) {
return sequence->Size;
}
int GetElement(const TSequence* sequence, int idx) {
assert(idx < sequence->Size);
return sequence->Data[idx];
}
int GetCapacity(const TSequence* sequence) {
return sizeof(sequence->Data)
/ sizeof(sequence->Data[0]);
}
void InsertAt(
TSequence* sequence, int idx, int value
) {
int size = GetSize(sequence);
assert(size + 1 < GetCapacity(sequence));
assert(idx <= size);
for (int i = size; i >= idx; --i) {
sequence->Data[i + 1] =
sequence->Data[i];
}
sequence->Data[idx] = value;
++sequence->Size;
}
46.
Тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence() {
TSequence sequence = {{0}, 0};
return sequence;
}
int GetSize(const TSequence* sequence) {
return sequence->Size;
}
int GetElement(const TSequence* sequence, int idx) {
assert(idx < sequence->Size);
return sequence->Data[idx];
}
int GetCapacity(const TSequence* sequence) {
return sizeof(sequence->Data)
/ sizeof(sequence->Data[0]);
}
void InsertAt(
TSequence* sequence, int idx, int value
) {
int size = GetSize(sequence);
assert(size + 1 < GetCapacity(sequence));
assert(idx <= size);
for (int i = size; i >= idx; --i) {
sequence->Data[i + 1] =
sequence->Data[i];
}
sequence->Data[idx] = value;
++sequence->Size;
}
47.
Тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence() {
TSequence sequence = {{0}, 0};
return sequence;
}
int GetSize(const TSequence* sequence) {
return sequence->Size;
}
int GetElement(const TSequence* sequence, int idx) {
assert(idx < sequence->Size);
return sequence->Data[idx];
}
int GetCapacity(const TSequence* sequence) {
return sizeof(sequence->Data)
/ sizeof(sequence->Data[0]);
}
void InsertAt(
TSequence* sequence, int idx, int value
) {
int size = GetSize(sequence);
assert(size + 1 < GetCapacity(sequence));
assert(idx <= size);
for (int i = size; i >= idx; --i) {
sequence->Data[i + 1] =
sequence->Data[i];
}
sequence->Data[idx] = value;
++sequence->Size;
}
48.
Построение перестановки через массив• a = N * None
• для i = 1, …, N делаем a[k] = i
• k – индекс t[i]-го None в а
• считаем с 0
• Таблица инверсий для a есть t:
• Обозначим FrozenElements(a)
множество всех перестановок, которые
совпадают с массивом а в позициях,
где в a не None
• После шага i таблица инверсий для
любой перестановки из
FrozenElements(a) имеет вид t1, t2, …, ti,
?, ?, …, ?
49.
Построение перестановки через массив• a = N * None
• для i = 1, …, N делаем a[k] = i
• k – индекс t[i]-го None в а
• считаем с 0
• Таблица инверсий для a есть t:
• Обозначим FrozenElements(a)
множество всех перестановок, которые
совпадают с массивом а в позициях,
где в a не None
• После шага i таблица инверсий для
любой перестановки из
FrozenElements(a) имеет вид t1, t2, …, ti,
?, ?, …, ?
50.
Построение перестановки через массив• a = N * None
• для i = 1, …, N делаем a[k] = i
• k – индекс t[i]-го None в а
• считаем с 0
• Таблица инверсий для a есть t:
• Обозначим FrozenElements(a)
множество всех перестановок, которые
совпадают с массивом а в позициях,
где в a не None
• После шага i таблица инверсий для
любой перестановки из
FrozenElements(a) имеет вид t1, t2, …, ti,
?, ?, …, ?
таблица инверсий t
массив а
2 3 6 4 0 2 2 1 0
1
2 3 6 4 0 2 2 1 0
1
2
2 3 6 4 0 2 2 1 0
1
2
2 3 6 4 0 2 2 1 0
1
2
4
3
3
2 3 6 4 0 2 2 1 0
5
1
2
4
3
2 3 6 4 0 2 2 1 0
5
1
2 6 4
3
2 3 6 4 0 2 2 1 0
5
1
2 6 4 7 3
2 3 6 4 0 2 2 1 0
5
1 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
51.
Построение перестановки через массив• a = N * None
• для i = 1, …, N делаем a[k] = i
• k – индекс t[i]-го None в а
• считаем с 0
• Таблица инверсий для a есть t:
• Обозначим FrozenElements(a)
множество всех перестановок, которые
совпадают с массивом а в позициях,
где в a не None
• После шага i таблица инверсий для
любой перестановки из
FrozenElements(a) имеет вид t1, t2, …, ti,
?, ?, …, ?
таблица инверсий t
массив а
2 3 6 4 0 2 2 1 0
1
2 3 6 4 0 2 2 1 0
1
2
2 3 6 4 0 2 2 1 0
1
2
2 3 6 4 0 2 2 1 0
1
2
4
3
3
2 3 6 4 0 2 2 1 0
5
1
2
4
3
2 3 6 4 0 2 2 1 0
5
1
2 6 4
3
2 3 6 4 0 2 2 1 0
5
1
2 6 4 7 3
2 3 6 4 0 2 2 1 0
5
1 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
52.
Построение перестановки через массив• a = N * None
• для i = 1, …, N делаем a[k] = i
• k – индекс t[i]-го None в а
• считаем с 0
• Таблица инверсий для a есть t:
• Обозначим FrozenElements(a)
множество всех перестановок, которые
совпадают с массивом а в позициях,
где в a не None
• После шага i таблица инверсий для
любой перестановки из
FrozenElements(a) имеет вид t1, t2, …, ti,
?, ?, …, ?
таблица инверсий t
массив а
2 3 6 4 0 2 2 1 0
1
2 3 6 4 0 2 2 1 0
1
2
2 3 6 4 0 2 2 1 0
1
2
2 3 6 4 0 2 2 1 0
1
2
4
3
3
2 3 6 4 0 2 2 1 0
5
1
2
4
3
2 3 6 4 0 2 2 1 0
5
1
2 6 4
3
2 3 6 4 0 2 2 1 0
5
1
2 6 4 7 3
2 3 6 4 0 2 2 1 0
5
1 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
53.
Построение перестановки через массив• a = N * None
• для i = 1, …, N делаем a[k] = i
• k – индекс t[i]-го None в а
• считаем с 0
• Таблица инверсий для a есть t:
• Обозначим FrozenElements(a)
множество всех перестановок, которые
совпадают с массивом а в позициях,
где в a не None
• После шага i таблица инверсий для
любой перестановки из
FrozenElements(a) имеет вид t1, t2, …, ti,
?, ?, …, ?
таблица инверсий t
массив а
2 3 6 4 0 2 2 1 0
1
2 3 6 4 0 2 2 1 0
1
2
2 3 6 4 0 2 2 1 0
1
2
2 3 6 4 0 2 2 1 0
1
2
4
3
3
2 3 6 4 0 2 2 1 0
5
1
2
4
3
2 3 6 4 0 2 2 1 0
5
1
2 6 4
3
2 3 6 4 0 2 2 1 0
5
1
2 6 4 7 3
2 3 6 4 0 2 2 1 0
5
1 8 2 6 4 7 3
2 3 6 4 0 2 2 1 0
5 9 1 8 2 6 4 7 3
54.
Построение перестановки через массивTSequence RestorePermutation2(
const TSequence* inversions
) {
TSequence permutation;
permutation = MakeEmptySequence();
int size = GetSize(inversions), none = -1;
for (int j = 0; j < size; ++j) {
InsertAt(&permutation, 0, none);
}
for (int j = 0; j < size; ++j) {
int idx = FindNthOccurence(
&permutation,
GetElement(inversions, j), none);
assert(idx != -1);
SetElement(&permutation, idx, j);
}
return permutation;
}
int FindNthOccurence(
const TSequence* sequence,
int n, int x
) {
int size = GetSize(sequence), count = 0;
for (int i = 0; i < size; ++i) {
if (GetElement(sequence, i) == x) {
if (count == n) {
return i;
}
++count;
}
}
return -1;
}
55.
Построение перестановки через массивTSequence RestorePermutation2(
const TSequence* inversions
) {
TSequence permutation;
permutation = MakeEmptySequence();
int size = GetSize(inversions), none = -1;
for (int j = 0; j < size; ++j) {
InsertAt(&permutation, 0, none);
}
for (int j = 0; j < size; ++j) {
int idx = FindNthOccurence(
&permutation,
GetElement(inversions, j), none);
assert(idx != -1);
SetElement(&permutation, idx, j);
}
return permutation;
}
int FindNthOccurence(
const TSequence* sequence,
int n, int x
) {
int size = GetSize(sequence), count = 0;
for (int i = 0; i < size; ++i) {
if (GetElement(sequence, i) == x) {
if (count == n) {
return i;
}
++count;
}
}
return -1;
}
56.
Построение перестановки через массивTSequence RestorePermutation2(
const TSequence* inversions
) {
TSequence permutation;
permutation = MakeEmptySequence();
int size = GetSize(inversions), none = -1;
for (int j = 0; j < size; ++j) {
InsertAt(&permutation, 0, none);
}
for (int j = 0; j < size; ++j) {
int idx = FindNthOccurence(
&permutation,
GetElement(inversions, j), none);
assert(idx != -1);
SetElement(&permutation, idx, j);
}
return permutation;
}
int FindNthOccurence(
const TSequence* sequence,
int n, int x
) {
int size = GetSize(sequence), count = 0;
for (int i = 0; i < size; ++i) {
if (GetElement(sequence, i) == x) {
if (count == n) {
return i;
}
++count;
}
}
return -1;
}
57.
Построение перестановки через массивTSequence RestorePermutation2(
const TSequence* inversions
) {
TSequence permutation;
permutation = MakeEmptySequence();
int size = GetSize(inversions), none = -1;
for (int j = 0; j < size; ++j) {
InsertAt(&permutation, 0, none);
}
for (int j = 0; j < size; ++j) {
int idx = FindNthOccurence(
&permutation,
GetElement(inversions, j), none);
assert(idx != -1);
SetElement(&permutation, idx, j);
}
return permutation;
}
int FindNthOccurence(
const TSequence* sequence,
int n, int x
) {
int size = GetSize(sequence), count = 0;
for (int i = 0; i < size; ++i) {
if (GetElement(sequence, i) == x) {
if (count == n) {
return i;
}
++count;
}
}
return -1;
}
58.
Итоговый тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence();
void InsertAt(
TSequence* sequence, int idx, int value
);
void SetElement(
TSequence* sequence,
int idx,
int GetCapacity(const TSequence* sequence);
int value
int GetSize(const TSequence* sequence);
) {
assert(idx < sequence->Size);
int GetElement(
const TSequence* sequence, int idx);
sequence->Data[idx] = value;
}
59.
Итоговый тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence();
void InsertAt(
TSequence* sequence, int idx, int value
);
void SetElement(
TSequence* sequence,
int idx,
int GetCapacity(const TSequence* sequence);
int value
int GetSize(const TSequence* sequence);
) {
assert(idx < sequence->Size);
int GetElement(
const TSequence* sequence, int idx);
sequence->Data[idx] = value;
}
60.
Итоговый тип TSequencetypedef struct TSequence {
int Data[100], Size;
} TSequence;
TSequence MakeEmptySequence();
void InsertAt(
TSequence* sequence, int idx, int value
);
void SetElement(
TSequence* sequence,
int idx,
int GetCapacity(const TSequence* sequence);
int value
int GetSize(const TSequence* sequence);
) {
assert(idx < sequence->Size);
int GetElement(
const TSequence* sequence, int idx);
sequence->Data[idx] = value;
}
61.
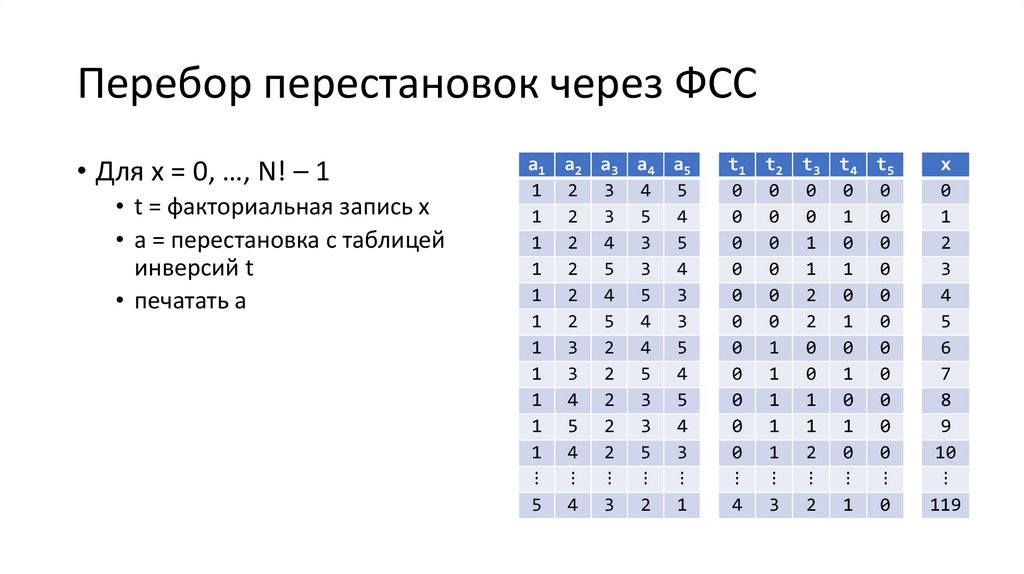
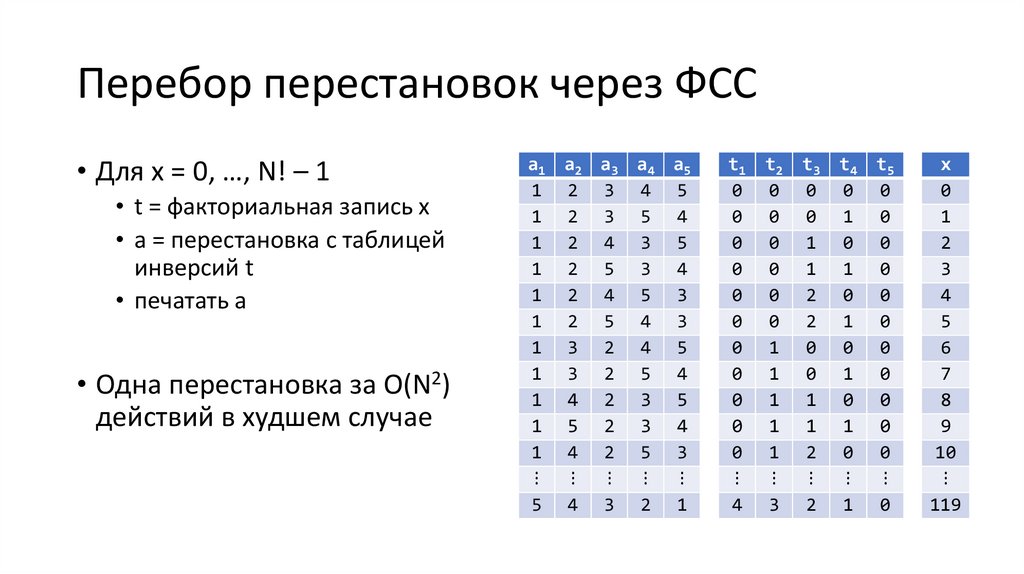
Факториальная система счисления• Факториальная система
счисления
• позиционная
• веса разрядов 0!, 1!, 2!, …, k!, …
• x = ∑k ≥ 1 tk ∙ (k – 1)!
• 0 ≤ tk < k
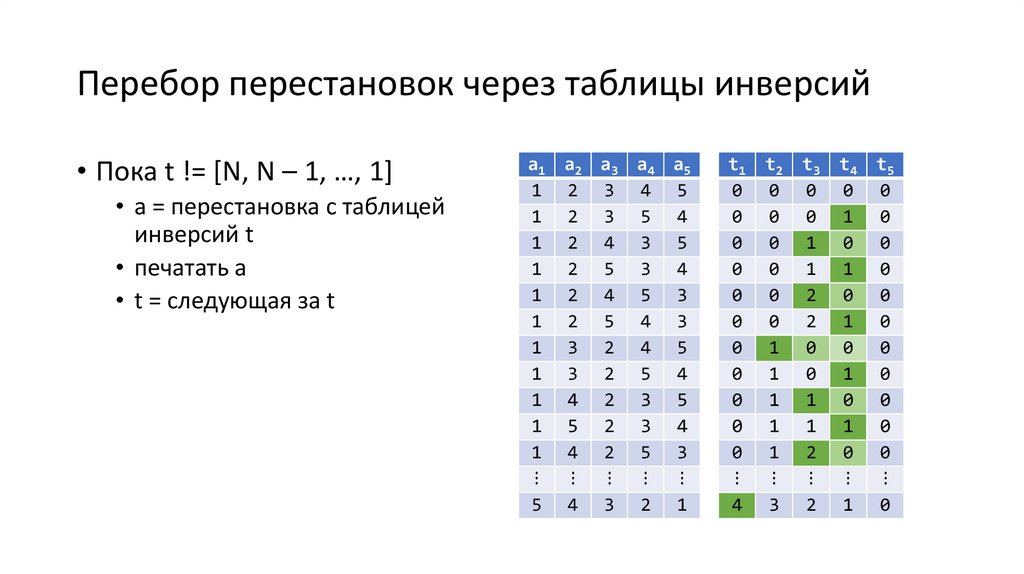
• Таблица инверсий – запись числа
от 0 до N! – 1 в факториальной
системе счисления
• С точностью до нумерации
разрядов
• Тождество – в подарок
• Пример
• N = 5, x = 88
• веса разрядов 1, 1, 2, 6, 24
• x = 0 ∙ 0! + 0 ∙ 1! + 2 ∙ 2! + 2 ∙ 3! + 3 ∙ 4!
=32200фсс





























































































 programming
programming informatics
informatics








