Полевая криминалистика (тема № 5)

1. МИНИСТЕРСТВО ВНУТРЕННИХ ДЕЛ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ КАЗЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

ВОЛГОГРАДСКАЯ АКАДЕМИЯ МВД
Кафедра криминалистической техники УНК ЭКД
Мультимедийная презентация:
Тема № 5
«Полевая криминалистика»
Разработчик
доцент каф. КТ УНК ЭКД
к.ф-м.н.
Прокофьева Е.В.
Волгоград 2021

2. Учебные вопросы:

1.
Понятие
и
элементы
полевой
криминалистики.
2. Измерения расстояний на местности.
3. Способы ориентирования и привязки на
местности.
4.
Использование
радиальной
системы
координат при осмотре места происшествия
на большой площади.

3. Вопрос 1. Понятие и элементы полевой криминалистики

Термин «полевая криминалистика»
появился в криминалистической науке
сравнительно недавно - в 1988 году.
Профессор Р. С. Белкин
(1922 – 2001 г.г.)
Основоположником данного учения
является выдающийся ученыйкриминалист Рафаил Самуилович
Белкин - теоретик и автор многих
фундаментальных трудов в области
криминалистики и судебной
экспертизы.

4. Понятие – полевая криминалистика

Полевая
криминалистика
техникокриминалистические средства и методы работы
с доказательствами, которые используются или
могут быть использованы не в кабинете
следователя или в лаборатории эксперта, а
непосредственно в «полевых» условиях - на
месте происшествия при его осмотре или
производстве на этом месте иных следственных
действий или исследовательских экспертных
операций.
Белкин Р.С. Криминалистика: проблемы, тенденции, перспективы.
От теории к практике. М., 2005. С. 37.

5. Элементы полевой криминалистики:

1. Приемы и способы обнаружения, фиксации
и изъятия следов преступления на открытой
местности;
2. Технические приемы проведения измерений
на пересеченной местности и в условиях
больших дальностей;
3. Способы ориентирования и привязки к
местности объектов и следов (определения
координат).

6. Содержание полевой криминалистики

Приемы и способы обнаружения, фиксации и
изъятия следов на открытой местности мало
отличаются от соответствующим приемов
применяемых в обычных условиях.
Поэтому в рамках полевой криминалистики
преимущественно рассматриваются вопросы,
связанные с:
- привязкой
объектов
на
местности
(определение их координат),
- фиксации
их
взаиморасположения
и
проведения измерений (угловых и линейных) на
открытой, пересеченной местности.

7. Вопрос 2. Измерения расстояний на местности

Измерение расстояний на местности с
использованием приемов и способов полевой
криминалистики включает:
2.1. измерение расстояний с помощью
дальномеров;
2.2. определении высот недоступных объектов
методом визирования;
2.3. определение расстояний по угловым
размерам предметов.

8. 2.1. Измерение расстояний с помощью дальномеров

Дальномер
–
это
устройство,
предназначенное для определения расстояния
от наблюдателя до объекта.
Используется в геодезии (при строительстве
путей сообщения), для наводки на резкость в
фотографии, в прицельных приспособлениях
оружия (для определения расстояний до целей) и
т.д.
Существует два вида дальномеров:
- оптические;
- физические.

9. Измерение расстояний с помощью оптических дальномеров

Измерение
расстояний
оптическими
дальномерами основано на определении
высоты h равнобедренного треугольника ABC,
например по известной стороне AB = Ɩ (базе) и
противолежащему острому углу β (т. н.
параллактическому углу).
При малых углах β (выраженных в радианах)
h = Ɩ / β. Одна из величин, Ɩ или β , обычно
является постоянной, а другая — переменной
(измеряемой). По этому признаку различают
оптические дальномеры постоянным углом и
дальномеры с постоянной базой.

10. Измерение расстояний с помощью оптических дальномеров

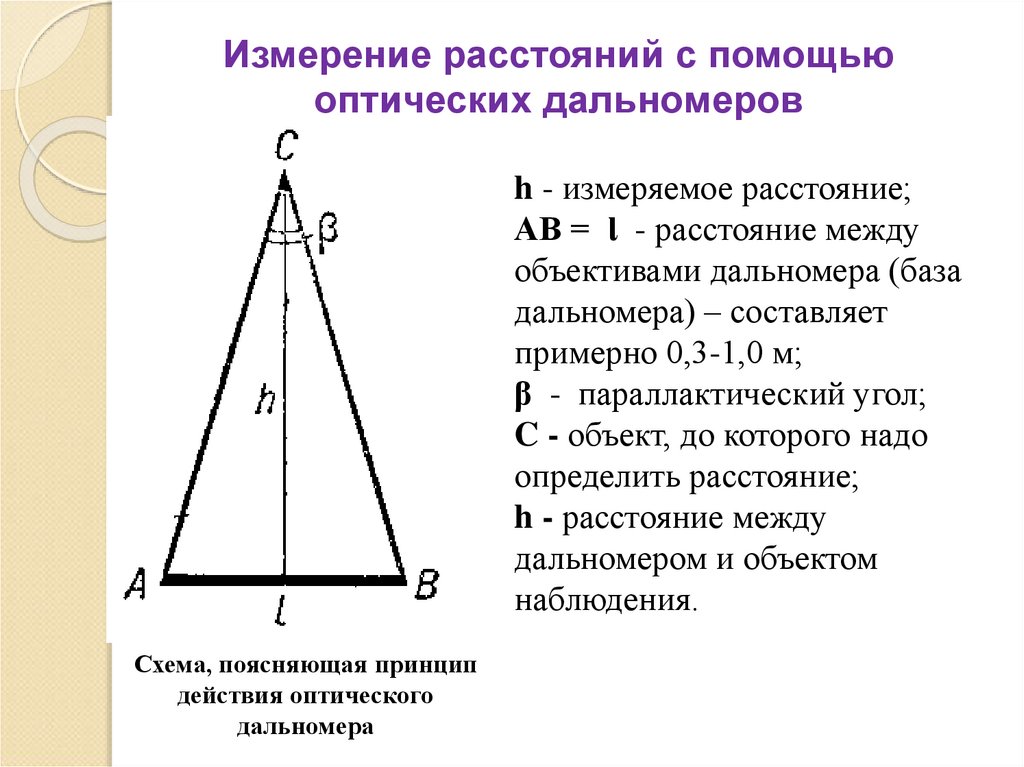
h - измеряемое расстояние;
AB = Ɩ - расстояние между
объективами дальномера (база
дальномера) – составляет
примерно 0,3-1,0 м;
β - параллактический угол;
C - объект, до которого надо
определить расстояние;
h - расстояние между
дальномером и объектом
наблюдения.
Схема, поясняющая принцип
действия оптического
дальномера

11.

Измерение расстояний с помощью оптических
дальномеров
Оптические
дальномеры
имеют
собственную постоянную базу.
Они разделяются на две группы:
монокулярные
и
бинокулярные
(стереоскопические).
При измерении через монокуляр дальномера
наблюдается выбранный объект. Этот объект
наблюдается в круге, разделенном по вертикали на две
части. Первоначально объект, наблюдаемый в окуляре,
«раздваивается» по вертикали. Путем вращения рейки
наблюдатель добивается совмещения двух половинок
объекта, после чего считывает по шкале показания
дальномера.

12.

Измерение расстояний с помощью оптических
дальномеров
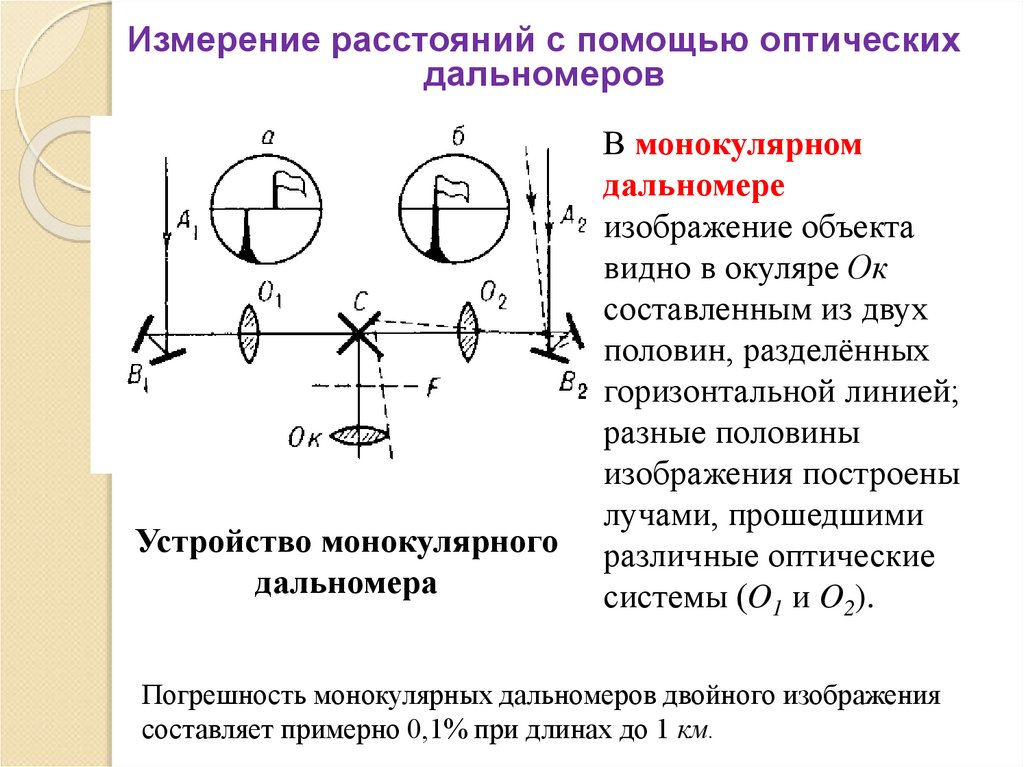
Устройство монокулярного
дальномера
В монокулярном
дальномере
изображение объекта
видно в окуляре Ок
составленным из двух
половин, разделённых
горизонтальной линией;
разные половины
изображения построены
лучами, прошедшими
различные оптические
системы (O1 и O2).
Погрешность монокулярных дальномеров двойного изображения
составляет примерно 0,1% при длинах до 1 км.

13.

Измерение расстояний с помощью оптических
дальномеров
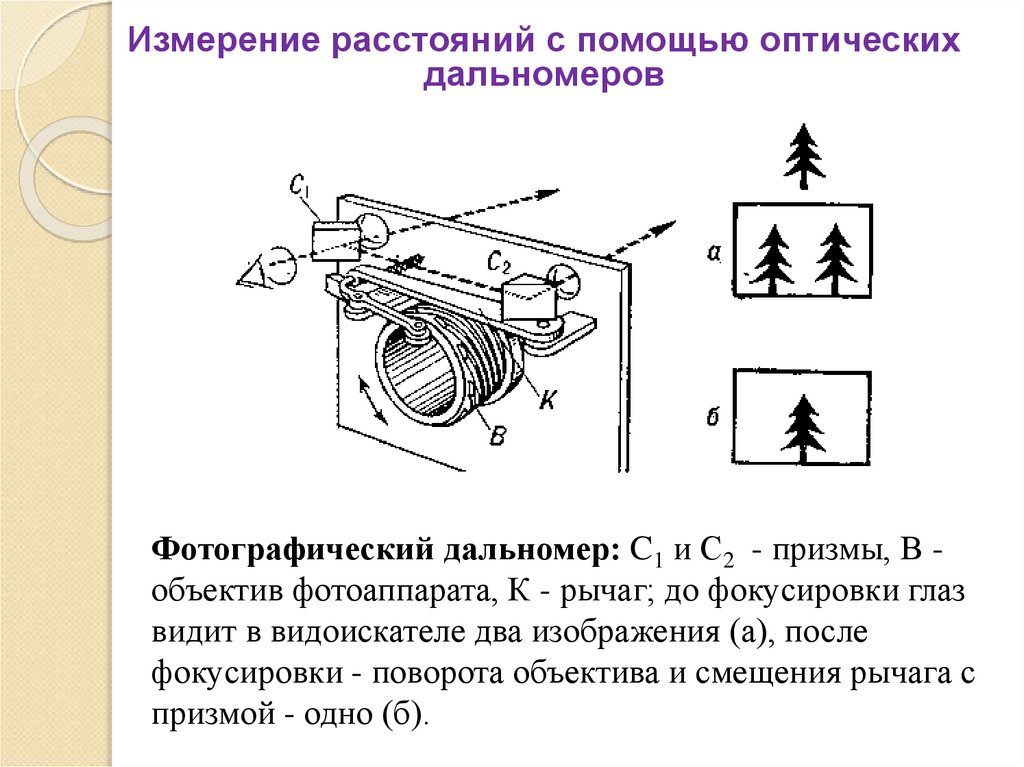
Фотографический дальномер: C1 и C2 - призмы, В объектив фотоаппарата, К - рычаг; до фокусировки глаз
видит в видоискателе два изображения (а), после
фокусировки - поворота объектива и смещения рычага с
призмой - одно (б).

14.

Измерение расстояний с помощью оптических
дальномеров
Действие стереоскопического дальномера основано
на
стереоскопическом
эффекте:
рассматриваемые
отдельно каждым глазом изображения сливаются в одно
объёмное, в котором ощущается разница в расположении
предметов по глубине.
Для определения расстояния до объекта изображение
объекта совмещают с изображением специальной метки
(«марки»), находящейся в фокальной плоскости
дальномера. Объект и «марка» должны как бы находиться
на одинаковом расстоянии от наблюдателя. Смещение
оптического компенсатора, требуемое для совмещения
«марки» и цели, пропорционально определяемому
расстоянию. Точность стереоскопического дальномера,
особенно с базой в несколько м, на порядок выше
точности монокулярных дальномеров.

15.

Измерение расстояний с помощью оптических
дальномеров
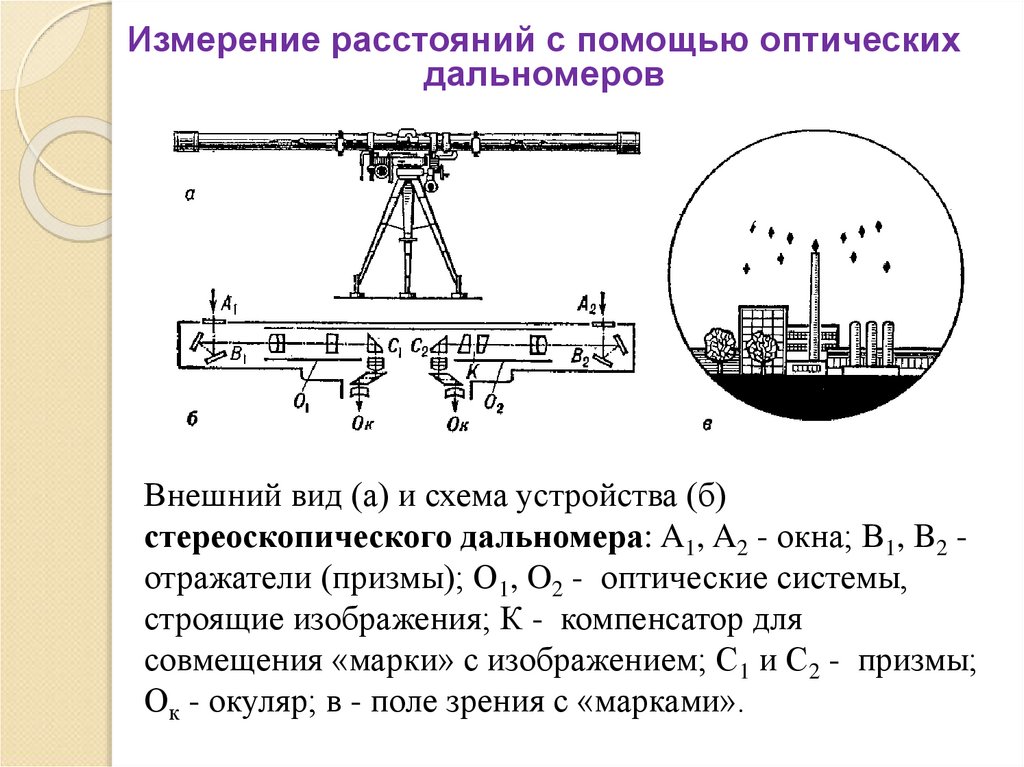
Внешний вид (а) и схема устройства (б)
стереоскопического дальномера: A1, A2 - окна; B1, B2 отражатели (призмы); O1, O2 - оптические системы,
строящие изображения; К - компенсатор для
совмещения «марки» с изображением; C1 и C2 - призмы;
Ок - окуляр; в - поле зрения с «марками».

16. Измерение расстояний с помощью физических дальномеров

Принцип действия физических дальномеров
состоит в измерении времени, которое затрачивает
посланный дальномером сигнал для прохождения
расстояния до объекта и обратно. Скорость
распространения сигнала (скорость света или звука)
считается известной.

17. Измерение расстояний с помощью физических дальномеров

Способность
электромагнитного
излучения
распространяться с постоянной скоростью дает
возможность определять дальность до объекта. При
этом для измерения расстояний используется
следующее соотношение:
где L - расстояние до объекта, c – скорость света в
вакууме, n – показатель преломления среды, в которой
распространяется излучение, t - время прохождения
импульса до объекта и обратно.

18.

Измерение расстояний с помощью физических
дальномеров
Лазерные дальномеры
Погрешность измерения составляет 0,01 % от дальности.

19.

2.2. Определении высот недоступных
объектов методом визирования
Для определения некоторых размеров объектов при осмотре места
происшествия приходится производить расчёты, когда нет
возможности по разным причинам непосредственно произвести
измерение.
Иногда при расследовании возникает необходимость в определении
значительных высот, непосредственное измерение которых, в
данных условиях невозможно или сопряжено с большими
трудностями.
Примеры такого рода дают, в частности, уголовные дела,
возбуждаемые в связи со смертью человека, разбившегося при
падении с высоты.
Другим примером является определение расстояния от уровня
земли до пулевого повреждения, находящегося на значительной
высоте. Знание этого расстояния необходимо для установления
места нахождения стрелявшего по делам об убийствах.

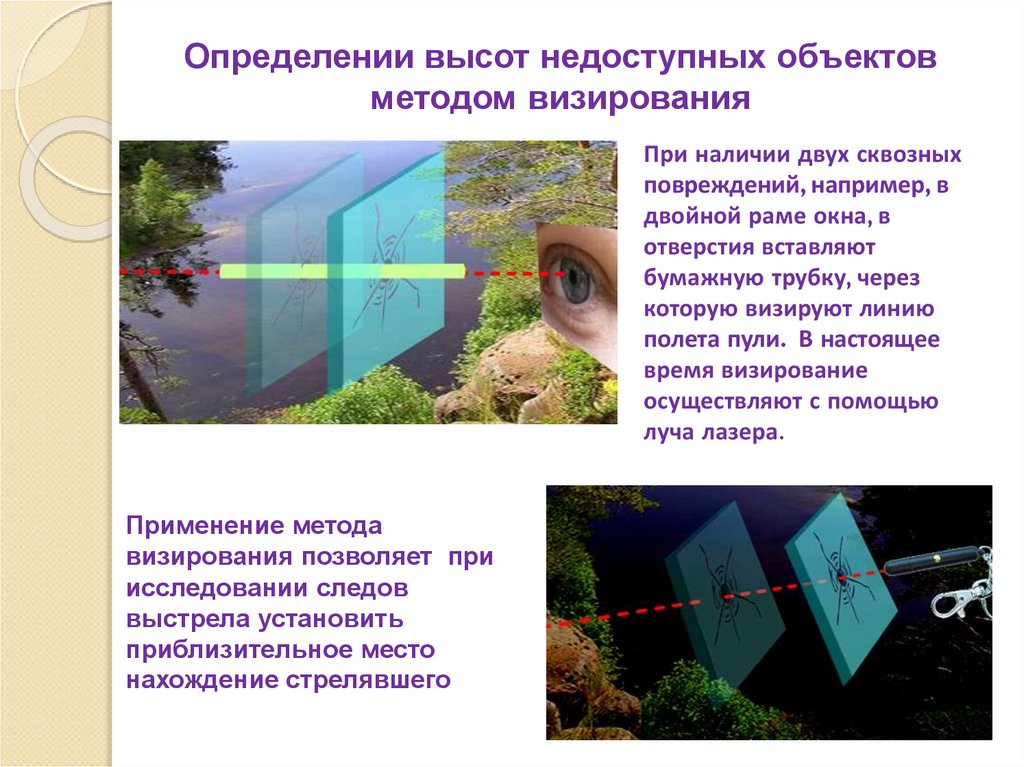
20. Определении высот недоступных объектов методом визирования

При наличии двух сквозных
повреждений, например, в
двойной раме окна, в
отверстия вставляют
бумажную трубку, через
которую визируют линию
полета пули. В настоящее
время визирование
осуществляют с помощью
луча лазера.
Применение метода
визирования позволяет при
исследовании следов
выстрела установить
приблизительное место
нахождение стрелявшего

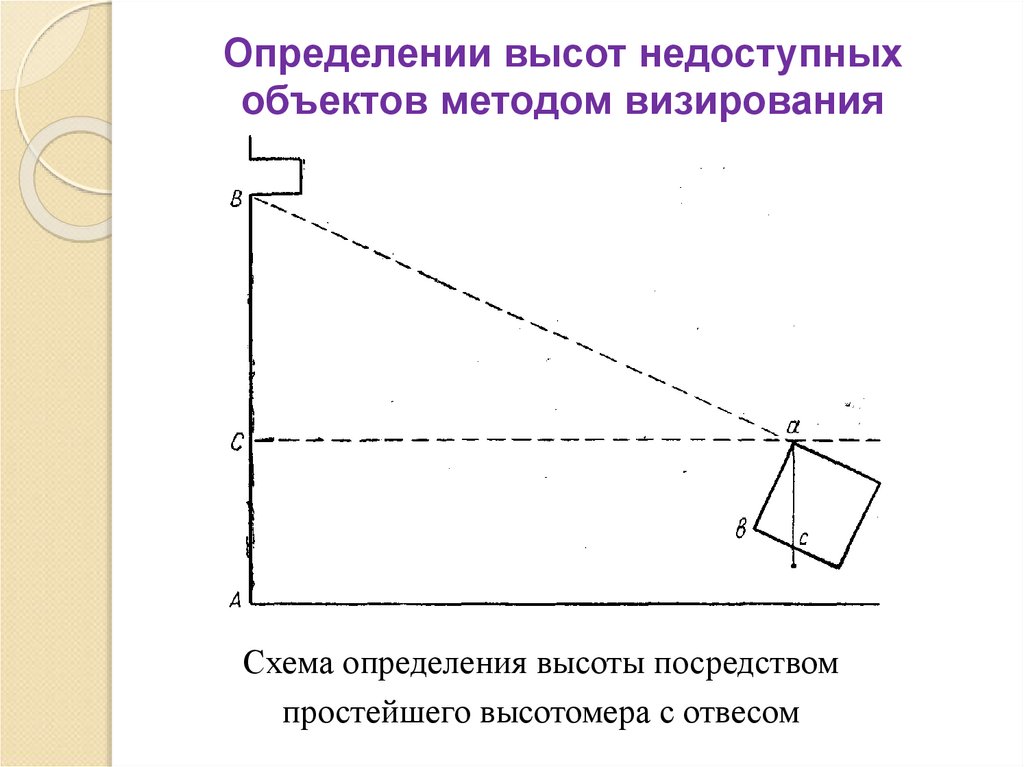
21. Определении высот недоступных объектов методом визирования

Схема определения высоты посредством
простейшего высотомера с отвесом

22.

Определении высот недоступных объектов
методом визирования
Для расчета высот можно применять высотомер,
представляющий собой квадрат из фанеры или
плотного картона. К одному из углов квадрата
прикреплен отвес.
При визировании одну из сторон, верхний конец
которой совмещается с точкой прикрепления отвеса,
располагают на одной прямой линии с точкой, высота
которой подлежит определению.
В зависимости от измеряемой высоты нить отвеса
пересекает противоположный край высотомера в той
или иной точке (С). Треугольники ВСа и авс подобны
как прямоугольные с соответственно параллельными
сторонами и равными острыми углами (СВа и асb).
Значит, ВС / bc = Cа / ab, отсюда ВС= Ca∙bc/ab.

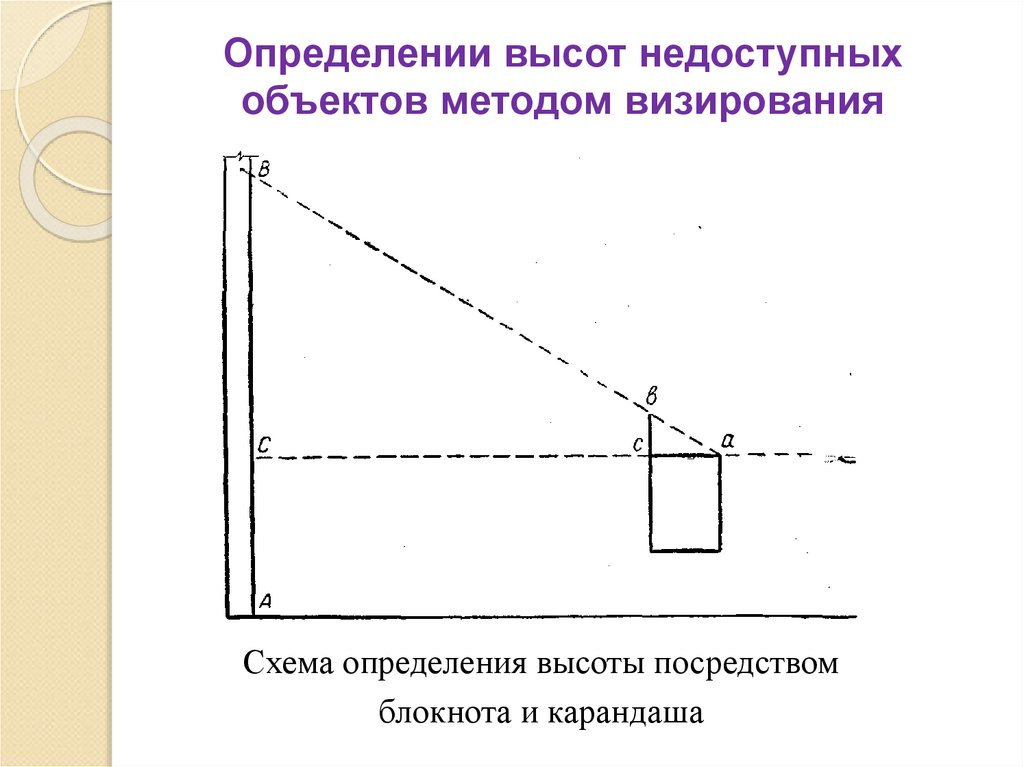
23. Определении высот недоступных объектов методом визирования

Схема определения высоты посредством
блокнота и карандаша

24.

Определении высот недоступных объектов
методом визирования
Высота может быть определена и при отсутствии
какого-либо прибора, с помощью записной книжки и
карандаша. Карандаш вставляется в имеющуюся при
записной книжке петельку или в промежуток между
корешком переплета и сброшюрованными листами.
Визирование заключается в расположении на одной
прямой линии верхнего, ближнего к наблюдателю угла
книжки, окончания выступающего отрезка карандаша
и точки, высоту которой требуется определить.
Подобие треугольников аВС и авс позволяет записать
уравнение BC / bc = aC / ac. Отсюда BC = aC·bc / ac.

25. Определении высот недоступных объектов методом визирования

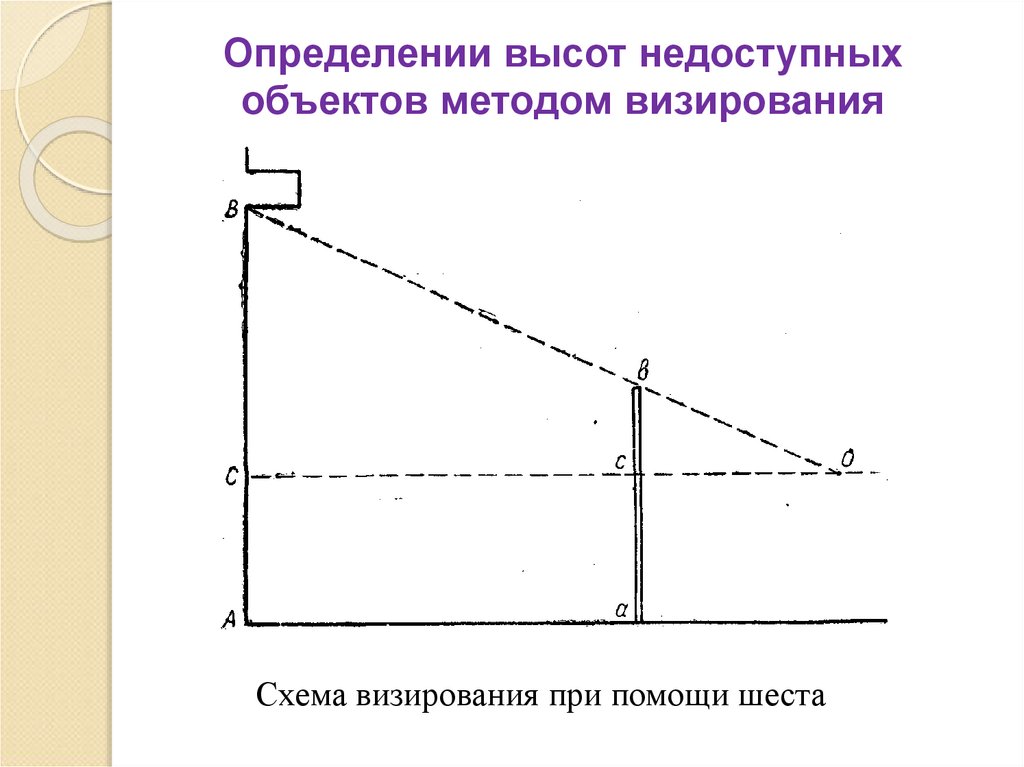
Схема визирования при помощи шеста

26.

Определении высот недоступных объектов
методом визирования
Третий способ - определения высоты при
помощи шеста. Здесь АВ - определяемая высота;
ab - шест; о точка расположения глаза
наблюдателя, bc - расстояние между концом шеста
и
высотой
расположения
глаза
человека,
производящего визирование над землей, ас высота расположения глаза при визировании равная
АС.
Ввиду подобия треугольников ВСо и bco
составляем уравнение BC / bc = oC/ oc.
Отсюда ВС = oC·bc / oc.

27.

2.3. Определение расстояний по угловым
размерам предметов
Линейные единицы измерения применяются для
обозначения видимой длинны, ширины или высоту
предмета (объекта, цель) в линейных величинах:
миллиметрах, сантиметрах, метрах, и т.д.
Угловые единицы измерения используются при
ориентировании на местности. Горизонтальные
(вертикальные) углы между направлениями на
местные предметы (цели) измеряют с помощью
угломерных
приборов
(устройств),
приборов
наблюдения или на глаз. Многие приборы,
применяемые для проведения измерений на
местности, имеют шкалы, оцифрованные в делениях
угломера.

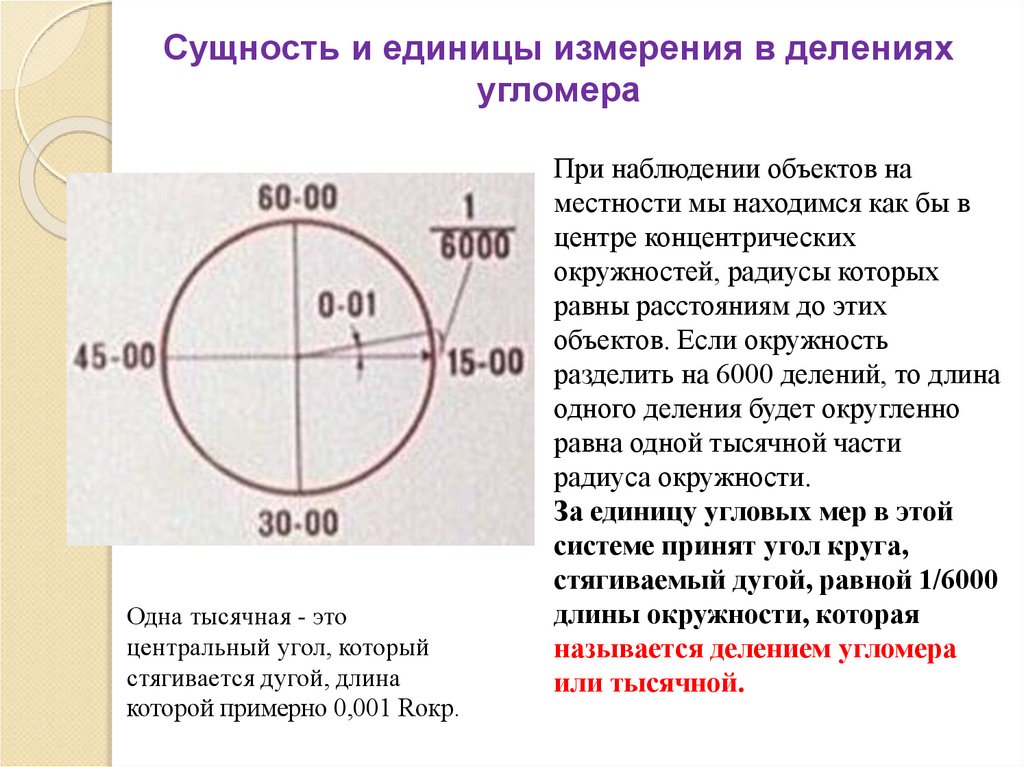
28. Сущность и единицы измерения в делениях угломера

Одна тысячная - это
центральный угол, который
стягивается дугой, длина
которой примерно 0,001 Rокр.
При наблюдении объектов на
местности мы находимся как бы в
центре концентрических
окружностей, радиусы которых
равны расстояниям до этих
объектов. Если окружность
разделить на 6000 делений, то длина
одного деления будет округленно
равна одной тысячной части
радиуса окружности.
За единицу угловых мер в этой
системе принят угол круга,
стягиваемый дугой, равной 1/6000
длины окружности, которая
называется делением угломера
или тысячной.

29.

Сущность и единицы измерения в делениях
угломера
Одно деление угломера – это величина центрального угла, который
соответствует дуге 1/6000 длины окружности, которая равна l=2πR.
Зависимость дальности от угловой и линейной величины предмета
определяется формулой:
В
Д
У
1000
где
В – известный линейный размер объекта, м;
У – угловая величина предмета, тыс.
При измерении углов в тысячных принято называть и записывать вначале
число сотен, а затем десятков и единиц тысячных. Если при этом сотен или
десятков не окажется, вместо них записывают нули (см. таблицу).
Удобство пользования системой измерения углов в тысячных состоит в том,
что единицей измерения угла служит линейный отрезок, равный тысячной
доле дистанции, что позволяет быстро, посредством арифметических действий
переходит от угловых измерений к линейным и наоборот.
Угол в тысячных
Записывается
Читается
1250
12-50
Двенадцать пятьдесят
156
1-56
Один пятьдесят шесть
35
0-35
Ноль тридцать пять
1
0-01
Ноль ноль одни

30. Измерение углов на местности при помощи линейки

Измерение углов с
помощью линейки
с миллиметровыми
делениями:
а – угол между
столбами линии
связи 0-32;
б – угол на дерево
0-21.
Если держать линейку перед собой на расстоянии 50 см, то одному
миллиметру на шкале линейки соответствует угол 0-02 (две тысячных).
Отсюда легко определить угловую величину для любых отрезков.
Например, для отрезка в 0,5 см угловая величина будет 10 тысячных (0-10),
для отрезка в 1 см-20 тысячных (0-20) и т.д.

31.

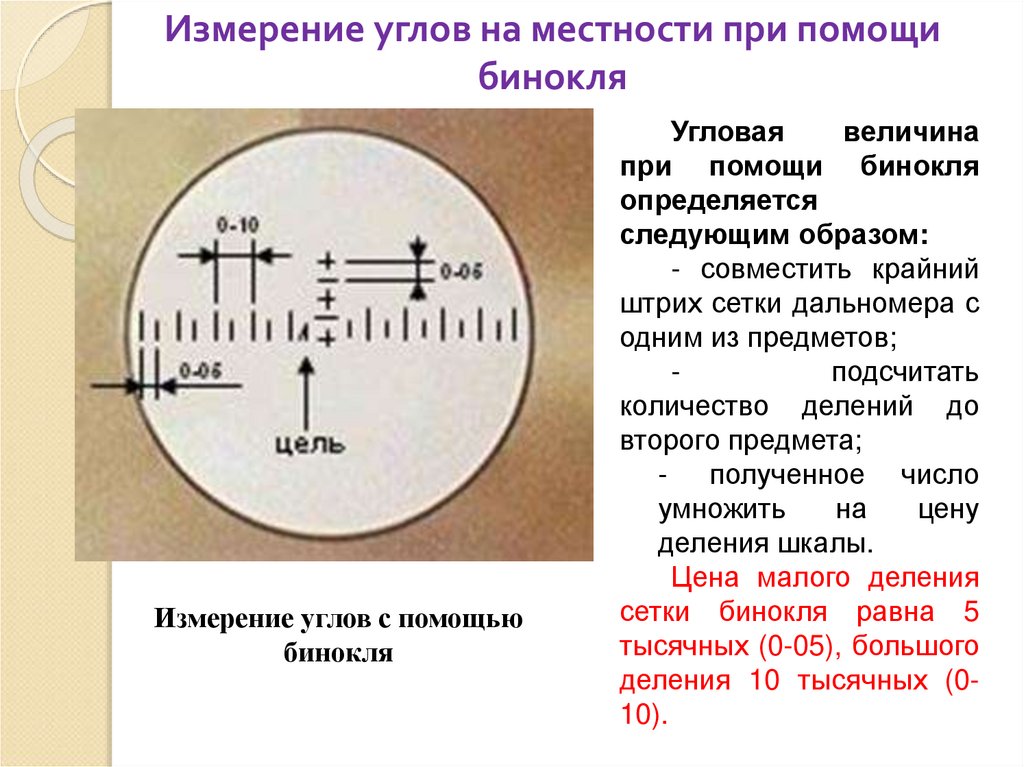
Измерение углов на местности при помощи
бинокля
Измерение углов с помощью
бинокля
Угловая
величина
при помощи бинокля
определяется
следующим образом:
- совместить крайний
штрих сетки дальномера с
одним из предметов;
подсчитать
количество делений до
второго предмета;
- полученное число
умножить
на
цену
деления шкалы.
Цена малого деления
сетки бинокля равна 5
тысячных (0-05), большого
деления 10 тысячных (010).

32. Вопрос 3. Способы ориентирования и привязки на местности

- способ Болотова (или способ засечек);
- по створам;
- по линейному и боковому ориентиру;
- при помощи систем спутниковой
навигации.

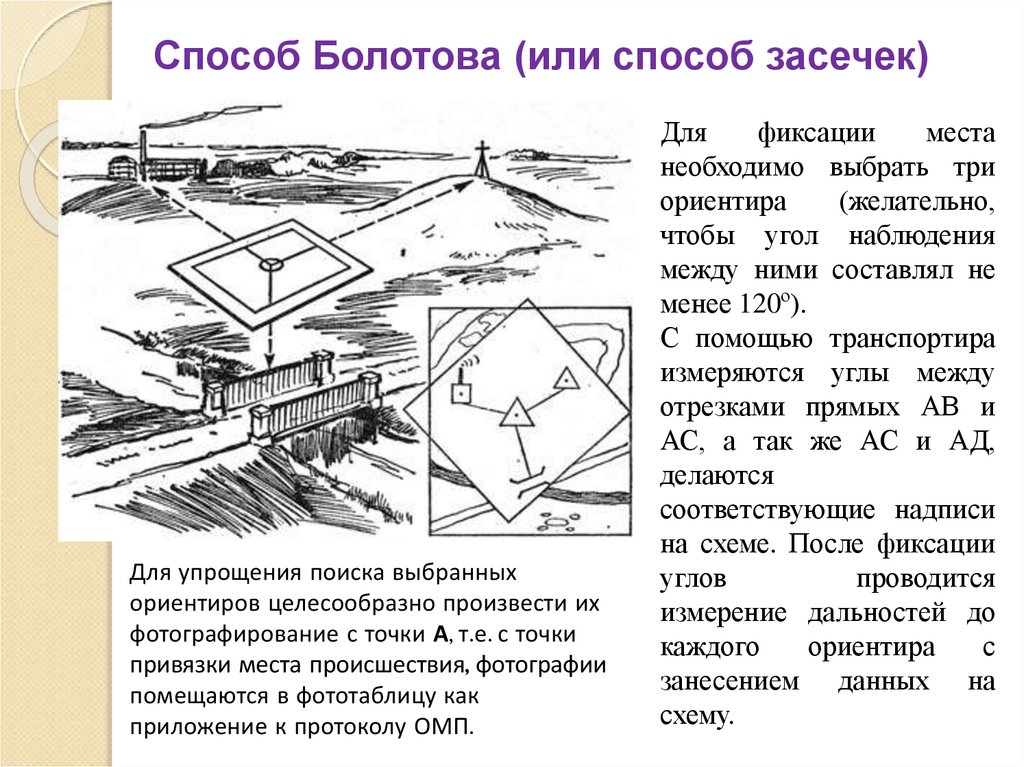
33. Способ Болотова (или способ засечек)

Для упрощения поиска выбранных
ориентиров целесообразно произвести их
фотографирование с точки А, т.е. с точки
привязки места происшествия, фотографии
помещаются в фототаблицу как
приложение к протоколу ОМП.
Для
фиксации
места
необходимо выбрать три
ориентира
(желательно,
чтобы угол наблюдения
между ними составлял не
менее 120º).
С помощью транспортира
измеряются углы между
отрезками прямых АВ и
АС, а так же АС и АД,
делаются
соответствующие надписи
на схеме. После фиксации
углов
проводится
измерение дальностей до
каждого
ориентира
с
занесением данных на
схему.

34. Способ привязки на местности по створам

Створом называется прямая линия, проходящая через точку
стояния и две точки местности, принадлежащие объектамориентирам, расположенным один за другим.
Данный способ применяется при условии хорошего обзора
местности и наличия на ней предметов или особенностей
местности, которые расположены на разной дальности в створе
друг с другом, и могут служить надежными ориентирами. На
местности выбираются два створа.

35. Способ привязки на местности по линейному и боковому ориентиру

В качестве линейного ориентира может быть участок
полевой дороги, линия электропередачи, берег реки,
озера или моря. Боковым ориентиром может быть любой
удаленный стационарный объект.

36.

Способ привязки на местности с помощью
систем спутниковой навигации
GPS (Global Positioning System)
– это спутниковая навигационная
система,
позволяющая
с
точностью не хуже 100 м
определить
местоположение
объекта: широту; долготу; высоту над уровнем моря, а
также направление и скорость его
движения.
GPS состоит из работающих в единой сети 24 спутников,
находящихся на 6 орбитах высотой около 17 000 км над
поверхностью Земли. Спутники постоянно движутся со
скоростью около 3 км/сек, совершая два полных оборота
вкруг планеты менее чем за 24 часа.

37. Способ привязки на местности с помощью систем спутниковой навигации

Навигационная
система позволяет
сформировать
следующие данные:
точные
географические
координаты
представленные в
табличной или
графической форме
на электронной карте
местности и т.д.
GPS приемник

38. Вопрос 4. Использование радиальной системы координат при осмотре места происшествия на большой площади

Наиболее доступная для анализа составленной
схемы является полярная система координат,
сущность которой сводится к выбору
одной
базисной точки на местности, генерального
направления
с
последующей
фиксацией
радиальных углов и дальностей до отдельных
объектов.
В качестве технических средств измерений
используются: для измерения вертикальных и
горизонтальных углов - теодолит или буссоль,
для измерения расстояний - дальномер.