Исследование траектории полета неуправляемого летательного аппарата

1.

КУРСОВАЯ РАБОТА на тему
«Исследование траектории
полета неуправляемого
летательного аппарата»

2.

Тематика курсовой работы
• В рамках выполнения курсовой работы студентам предлагается
разработать численную модель, алгоритм и программу расчета
неуправляемого полета летательного аппарата (ЛА) на языке
программирования С++ с заданными начальными условиями по
известной математической модели, выполнить тестирование
программы, провести вычислительные эксперименты и анализ
полученных результатов, построить графики траектории полета ЛА,
сделать практические выводы.
• Выполнение курсовой работы направлено на овладение
практическими навыками использования ЭВМ для численного
решения обыкновенных дифференциальных уравнений и их систем, а
также проведение вычислительных экспериментов по решению
практических задач.

3.

4.

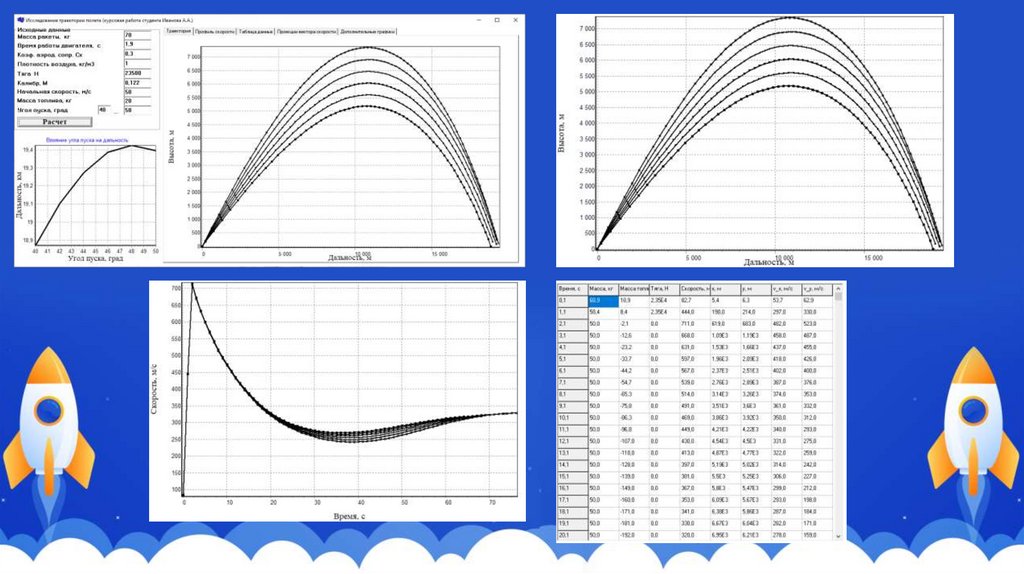
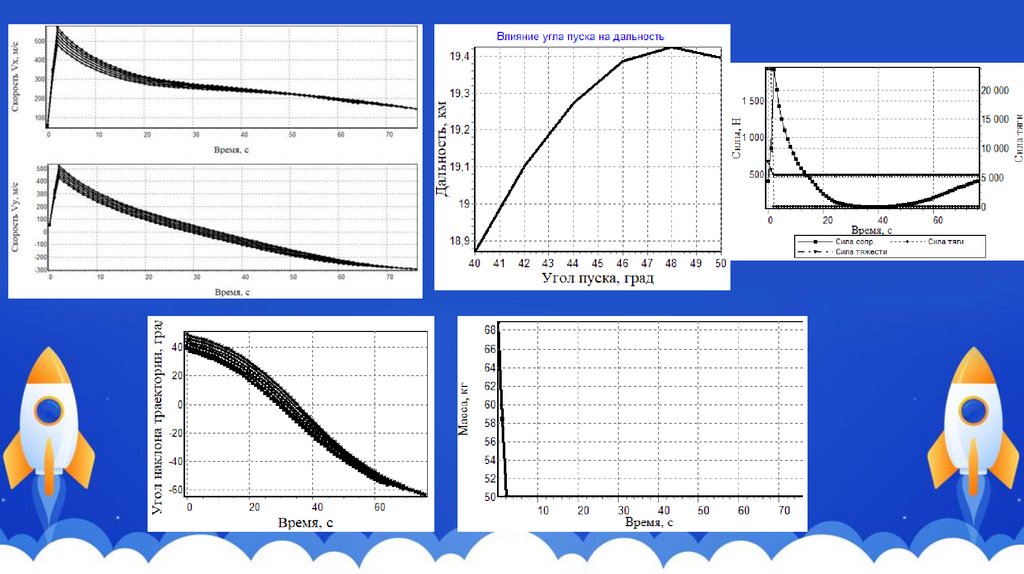
Основы теории
Траектория полета делится на два участка: активный (с работающим
двигателем, то есть на ЛА действует сила тяги) и пассивный (с неработающим
двигателем, соответственно, сила тяги отсутствует).
Для упрощения расчетов примем следующие допущения:
1
Земля плоская и ее вращение отсутствует
2
Движение происходит без колебаний вокруг продольной оси ракеты
3
Полет проходит на высотах, где изменением плотности воздуха и
ускорения свободного падения можно пренебречь
4
Сила тяги Р постоянна в течение всего времени
активного участка ta, т.е. P=const

5.

Физическая модель движения
На рисунке показана физическая модель
движения ЛА, согласно которой
ЛА
заменяем материальной точкой, в которой
приложены все силы, действующие на
него. Такой точкой является центр масс. В
произвольный момент времени на ЛА
действуют следующие силы: Р – сила тяги,
Р
Х
ϴ
G=mg
Х – сила лобового сопротивления,
G=mg – сила тяжести.
ЛА запускается при следующих начальных условиях:
с земли (x0,y0)=(0,0) под углом θ=θ0 к горизонту со скоростью V=V0 в
момент времени t = 0.

6.

Математическая модель движения
С учетом принятых допущений центр масс
Р
ракеты будет совершать поступательное
движение
под
действием
сил,
Х
действующих в одной плоскости: Методика
расчета
траектории
базируется
на
основном законе механики (втором законе
G=mg
Ньютона),
связывающем
ускорение,
ϴ
испытываемое точкой массой m под
действием силы F: