Similar presentations:
Графы. Элементы графов. Виды графов и операции над ними
1.
2.
• Теория графов представляетсобой раздел математики,
имеющий широкие практические
приложения.
• Теория графов – область
дискретной математики,
особенностью которой является
геометрический подход к изучению
объектов.
3.
Термин "граф" впервые появился в книгевенгерского математика Д. Кенига в 1936
г., хотя начальные важнейшие теоремы о
графах восходят к Л. Эйлеру.
4.
В основе теории лежит понятиеГраф - совокупность конечного числа
точек, называемых вершинами графа,
и попарно соединяющих некоторые из
этих вершин линий, называемых
ребрами или дугами графа. Иногда
граф в целом можно обозначать
одной заглавной буквой.
Графом G V , X
называется пара
двух конечных множеств: множество
точек V и множество линий X (ребер,
дуг), соединяющих некоторые пары точек.
5.
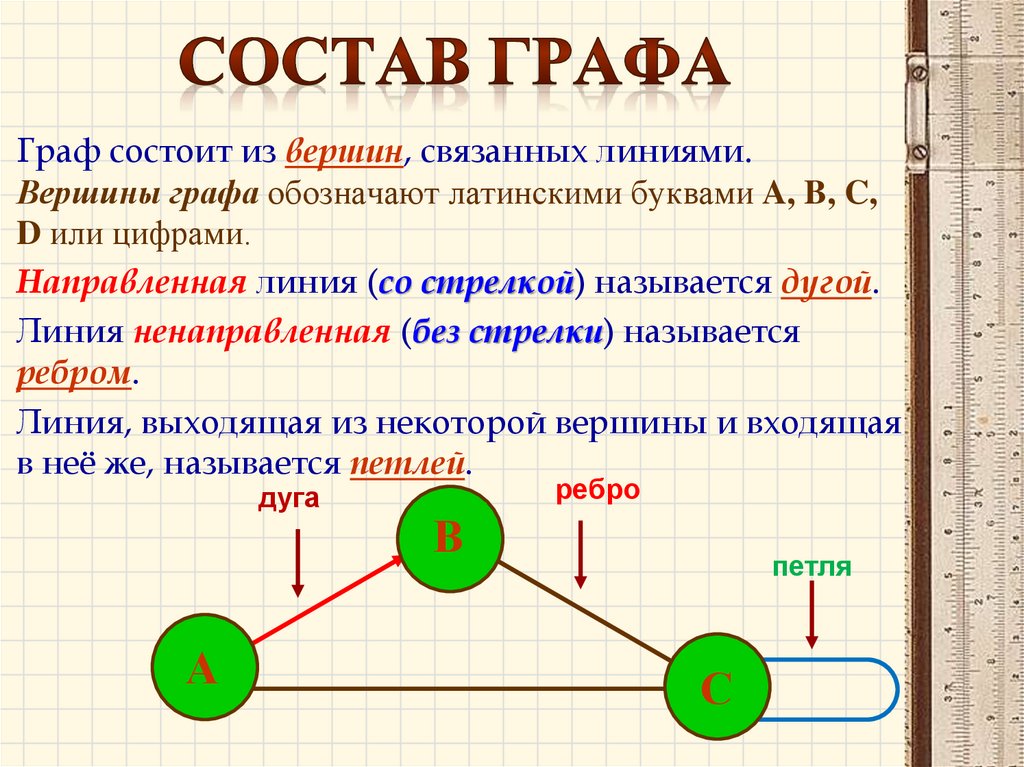
Граф состоит из вершин, связанных линиями.Вершины графа обозначают латинскими буквами A, B, C,
D или цифрами.
Направленная линия (со стрелкой) называется дугой.
Линия ненаправленная (без стрелки) называется
ребром.
Линия, выходящая из некоторой вершины и входящая
в неё же, называется петлей.
дуга
А
ребро
В
петля
С
6.
Ориентированный граф граф, вершины которого соединены дугами. Спомощью таких графов могут быть представлены
схемы односторонних отношений.
Юра
Аня
Маша
Коля
Витя
7.
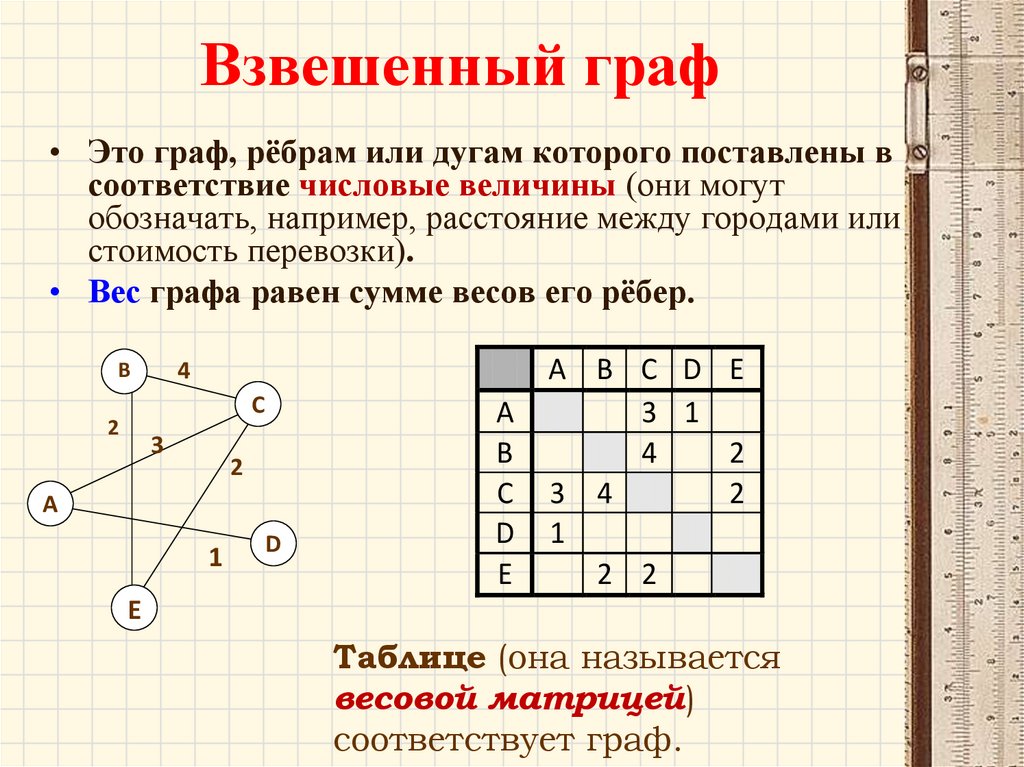
Взвешенный граф• Это граф, рёбрам или дугам которого поставлены в
соответствие числовые величины (они могут
обозначать, например, расстояние между городами или
стоимость перевозки).
• Вес графа равен сумме весов его рёбер.
4
B
C
2
3
2
A
1
D
A
B
C
D
Е
A B C D Е
3 1
4
2
3 4
2
1
2 2
E
Таблице (она называется
весовой матрицей)
соответствует граф.
8.
Если ребро графа G соединяет две еговершины V и W, (т.е. V ,W X ), то говорят,
что это ребро им инцидентно.
• Две вершины графа называются смежными,
если существует инцидентное им ребро: на
рисунке смежными являются вершины А и
В, А и С.
А
С
В
9.
Если граф G имеет ребро , у которогоначало и конец совпадают, то это ребро
называется петлёй. На рисунке ребро q(С, С)
– петля.
q
E
С
A
D
B
10.
Два ребра называются смежными, если ониимеют общую вершину.
На
рисунке
смежными
являются,
например, рёбра х1 и х2 с общей вершиной С.
D
х5
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A
11.
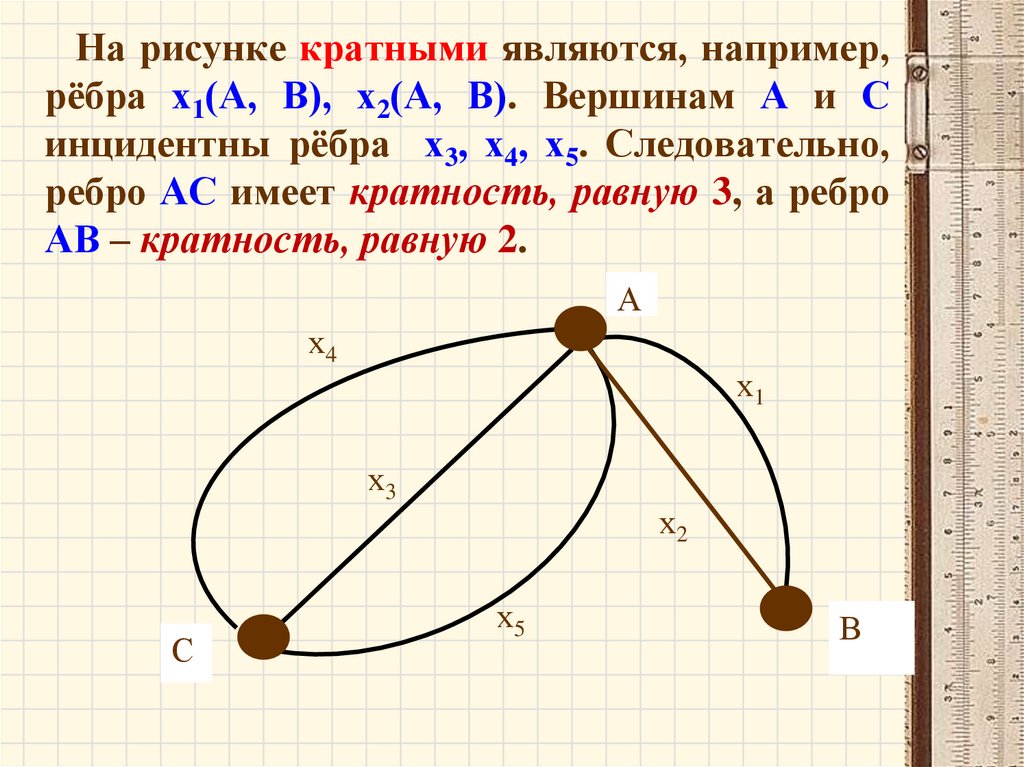
• Рёбра, которые начинаются в одной итой же вершине, заканчиваются также
в одной и той же вершине, называются
кратными, или параллельными.
• Количество одинаковых пар вида (V ,W )
называется кратностью ребра (V ,W )
• Число рёбер, инцидентных вершине А,
называется степенью этой вершины и
deg( A) (от англ. degree
обозначается
– степень).
12.
На рисунке кратными являются, например,рёбра х1(А, В), х2(А, В). Вершинам А и С
инцидентны рёбра х3, х4, х5. Следовательно,
ребро АС имеет кратность, равную 3, а ребро
АВ – кратность, равную 2.
А
х4
х1
х3
С
х2
х5
В
13.
На рисунке вершина А имеет степень,равную 1, вершина С – 4, вершина D – 2.
Записывается это в виде: deg(A)=1, deg(C)=4,
deg(D)=2.
D
х5
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A
14.
• Вершина графа, имеющая степень, равнуюнулю, называется изолированной.
• Граф, состоящий из изолированных вершин,
называется нуль-графом.
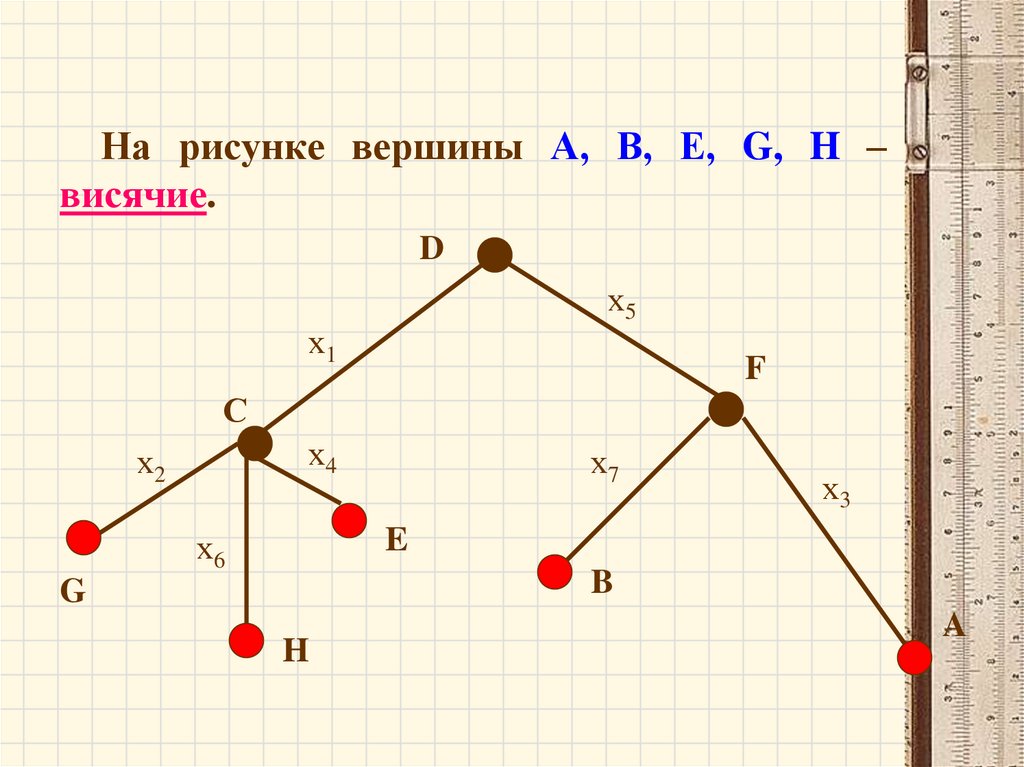
• Вершина графа, имеющая степень, равную 1,
называется висячей.
• Граф, не имеющий ребер (дуг), называется
пустым.
E
C
A
D
B
На рисунке вершина
Е – изолированная:
deg(E)=0.
15.
На рисунке вершины А, В, Е, G, H –висячие.
D
х5
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A
16.
Теорема 1. В графе G V , Xсумма
степеней всех его вершин – число чётное,
равное удвоенному числу рёбер графа:
n
deg(V ) 2m
i 1
где n V
i
- число вершин;
m X - число рёбер графа.
17.
Вершина называется чётной (нечётной),если её степень – чётное (нечётное) число.
На рисунке deg(D)=2, deg(F)=3, значит у
графа вершина D является чётной, а F –
нечётной.
х5
D
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A
18.
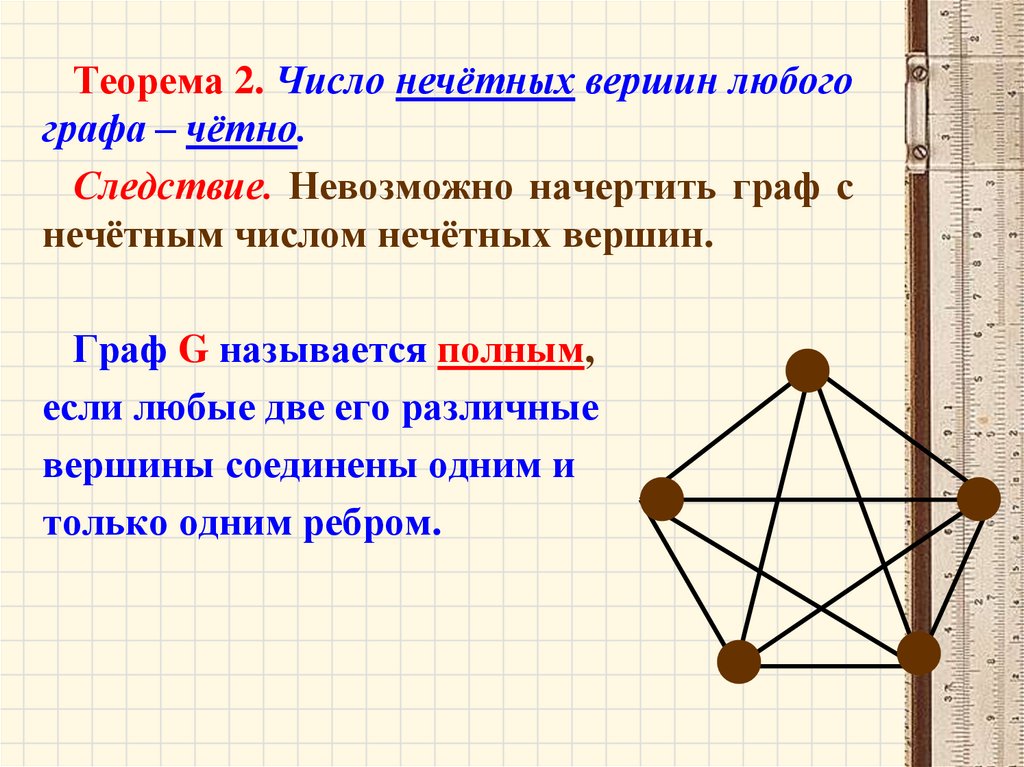
Теорема 2. Число нечётных вершин любогографа – чётно.
Следствие. Невозможно начертить граф с
нечётным числом нечётных вершин.
Граф G называется полным,
если любые две его различные
вершины соединены одним и
только одним ребром.
19.
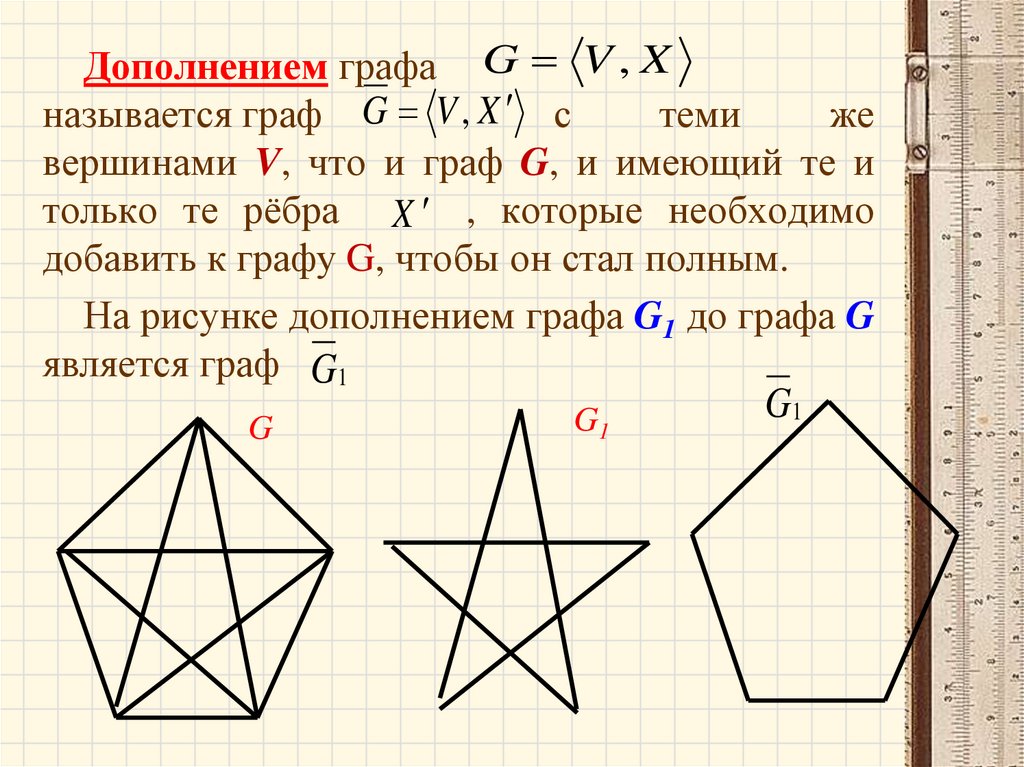
Дополнением графа G V , Xназывается граф G V , X с
теми
же
вершинами V, что и граф G, и имеющий те и
только те рёбра X , которые необходимо
добавить к графу G, чтобы он стал полным.
На рисунке дополнением графа G1 до графа G
является граф G1
G
G1
G1
20.
• Путем в ориентированном графе называетсяпоследовательность дуг, в которой конечная
вершина любой дуги, отличной от последней,
является начальной вершиной следующей
дуги.
• Вершина, от которой проложен маршрут,
называется началом пути, вершина в конце
маршрута — конец пути.
• Путь, в котором каждая вершина используется
не более одного раза, называется простым
путем.
• Длиной пути в графе называется количество
дуг (ребер), составляющих этот путь.
21.
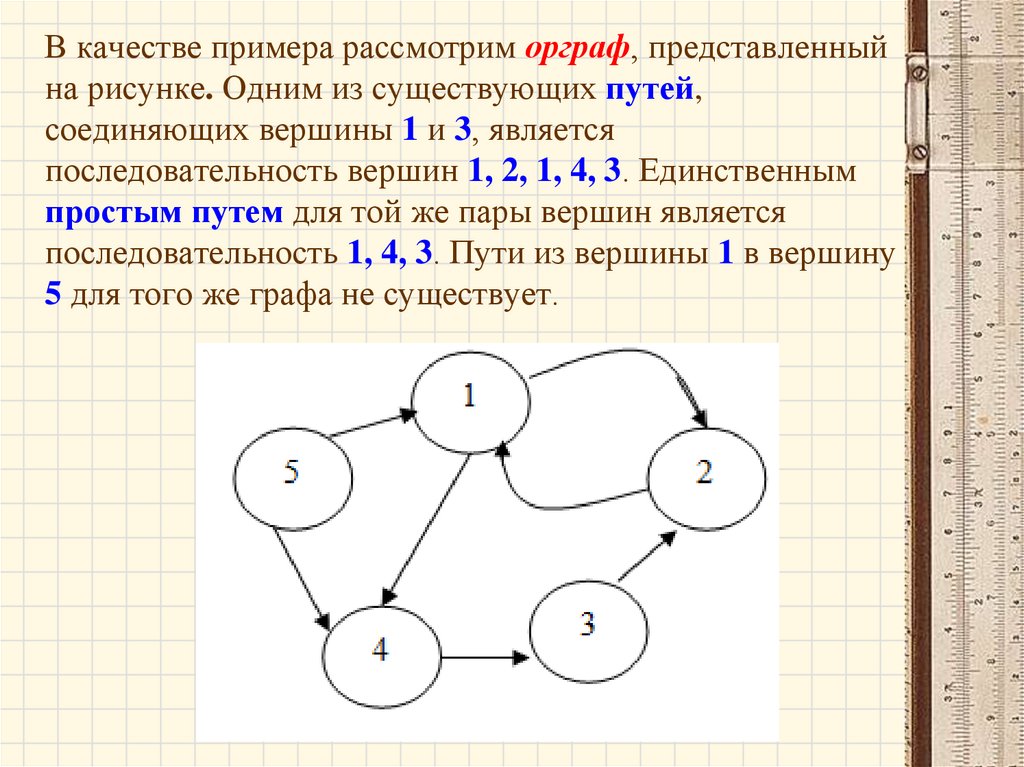
В качестве примера рассмотрим орграф, представленныйна рисунке. Одним из существующих путей,
соединяющих вершины 1 и 3, является
последовательность вершин 1, 2, 1, 4, 3. Единственным
простым путем для той же пары вершин является
последовательность 1, 4, 3. Пути из вершины 1 в вершину
5 для того же графа не существует.
22.
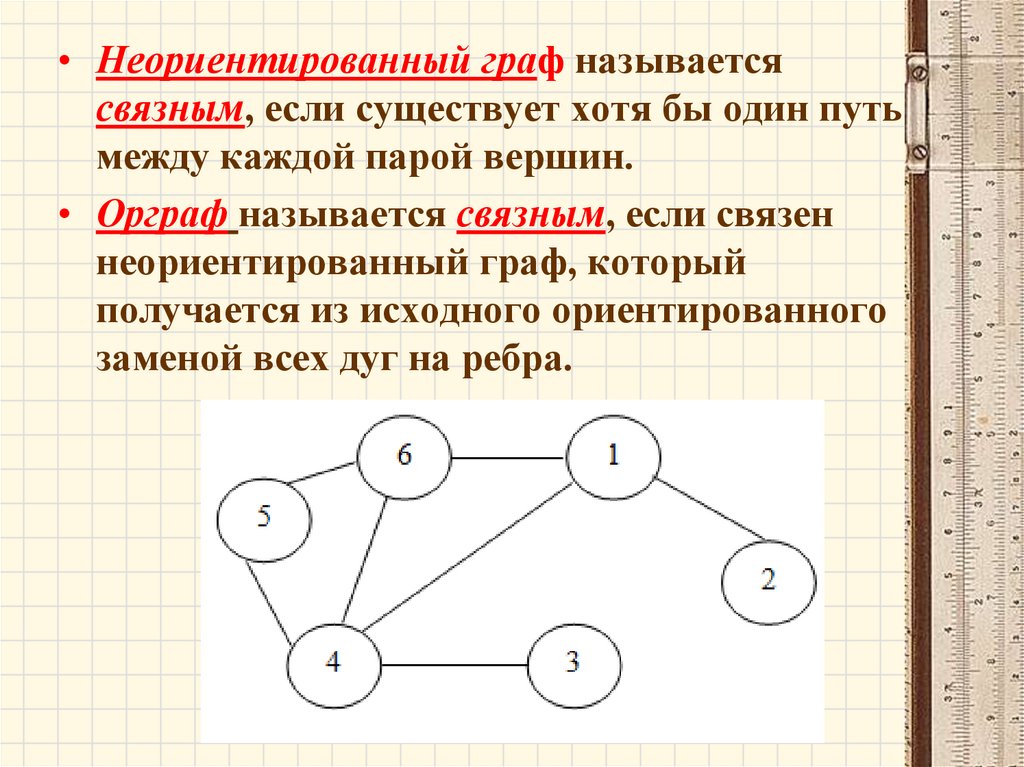
• Неориентированный граф называетсясвязным, если существует хотя бы один путь
между каждой парой вершин.
• Орграф называется связным, если связен
неориентированный граф, который
получается из исходного ориентированного
заменой всех дуг на ребра.
23.
• Путь называется замкнутым, еслиначальная и конечная вершины совпадают.
• Замкнутый путь называется циклом, если
все его вершины (кроме начальной и
конечной) различны.
• Рассмотрим граф. Для него путь 2, 1, 6, 5, 4,
1, 2 является замкнутым; а путь 1, 6, 5, 4, 1
является циклом.
24.
• Последовательность попарно смежныхвершин неориентированного графа, т.е.
последовательность рёбер
неориентированного графа, в которой
вторая вершина предыдущего ребра
совпадает с первой вершиной следующего,
называется маршрутом.
• Число рёбер маршрута называется длиной
маршрута.
• Если начальная вершина маршрута
совпадает с конечной, то такой маршрут
называется замкнутым или циклом.
25.
На рисунке HCDFD – маршрут длиной 4.Обозначение: |HCDFD|=4. Маршрут принято
задавать как
последовательность рёбер,
поскольку это удобно при наличии кратных
рёбер.
х
5
D
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A
26.
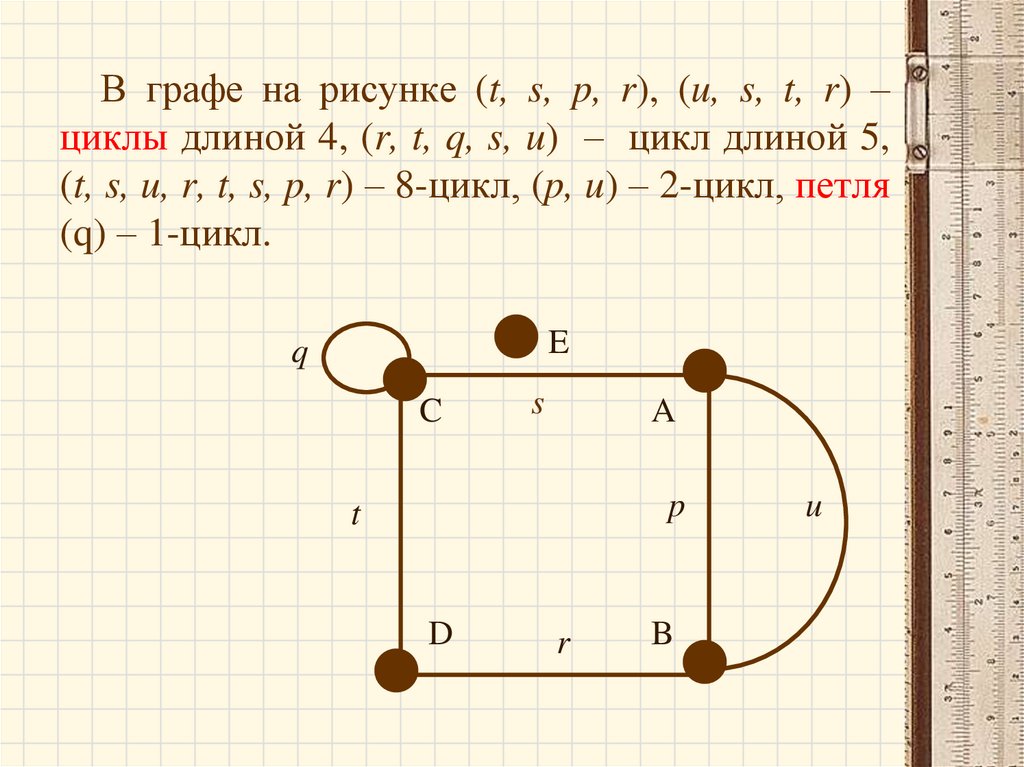
В графе на рисунке (t, s, p, r), (u, s, t, r) –циклы длиной 4, (r, t, q, s, u) – цикл длиной 5,
(t, s, u, r, t, s, p, r) – 8-цикл, (p, u) – 2-цикл, петля
(q) – 1-цикл.
E
q
C
s
A
p
t
D
r
B
u
27.
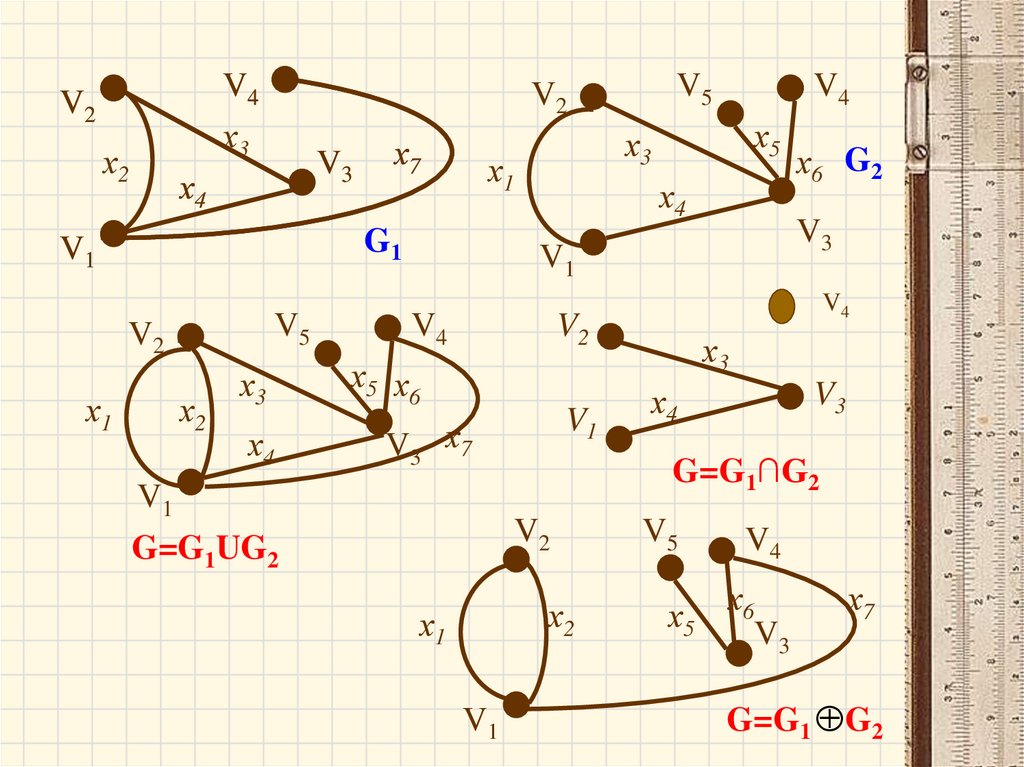
Объединением графов G1 (V1 , X 1 ) и G2 (V2 , X 2 )называется граф G G1 , G2 множество
вершин
которого V V1 V2 , а множество рёбер X X 1. X 2
Пересечением графов G1 и G2
называется граф G G1 G2 , для которого
X X 1 X 2 - множество рёбер, а V V1 V2 множество вершин.
Кольцевой суммой двух графов называется
граф G G1 G2 ,порождённый
множеством
вершин V V1 V2 и множеством рёбер ( X 1 X 2 ) \ ( X 1 X 2 )
, т.е. множеством рёбер, содержащихся либо в G1 ,
либо в G2 , но не в G1 G2
.
28.
V4х3
V2
х2
V3
х4
х1
х7
V5
х2
х3
х4
V4
х5
х3
х1
G1
V1
V2
V5
V2
х4
V3
V1
V4
V4
V2
х5 х6
V1
V3 х7
V1
G=G1UG2
х2
V1
х3
V3
х4
G=G1∩G2
V2
х1
х6 G 2
V5
V4
х5 х6V
3
х7
G=G1 G2
29.
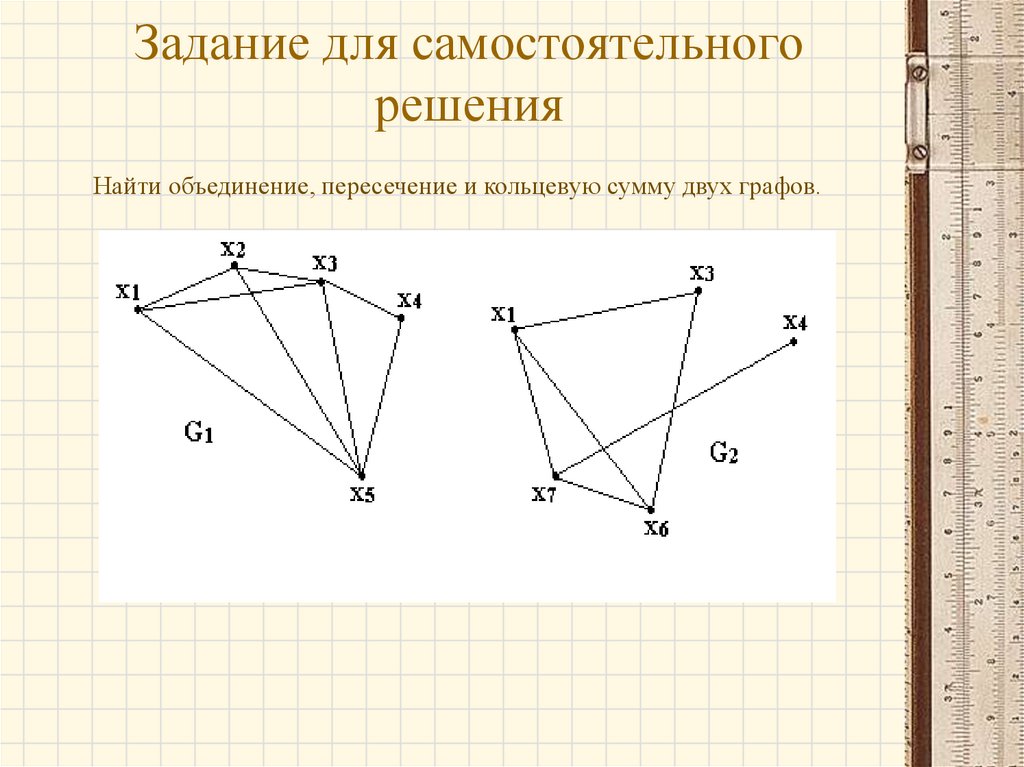
Задание для самостоятельногорешения
Найти объединение, пересечение и кольцевую сумму двух графов.


















 mathematics
mathematics








