Similar presentations:
Основы логики и логические операции
1. Основы логики и логические операции
2.
Логика – это наука о формах испособах мышления.
Понятие – это форма мышления, фиксирующая
основные, существенные признаки объекта.
Высказывание – это форма мышления, в
которой что-либо утверждается или отрицается
о свойствах разных предметов и отношений
между ними. Высказывание может быть либо
истинно либо ложно.
Умозаключение – это форма мышления, с
помощью которой из одного или нескольких
суждений может быть получено новое
суждение.
3. Создатель алгебры логики ХIХ в. английский математик Джордж Буль.
Алгебра логики — этоматематический аппарат, с помощью
которого записывают, вычисляют,
упрощают и преобразовывают
логические высказывания.
Американец Клод Шеннон раскрыл
связи между двоичным способом
хранения информации, алгеброй
логики и электрическими схемами.
4. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ КОМПЬЮТЕРА
Логический элемент компьют ера — это частьэлектронной логической схемы, которая
реализует элементарную логическую
функцию.
Базовые логические элементы реализуют
основные логические операции: И, ИЛИ,
НЕ, И-НЕ, ИЛИ-НЕ. Каждая логическая
операция имеет свою электронную схему.
5.
• На основе базовых логическихэлементов конструируют главную
часть процессора – сумматор
(одноразрядный и многоразрядный),
полусумматор.
• Сумматор – электронная схема,
выполняющая суммирование
двоичных чисел.
• Логические элементы компьютера
оперируют с сигналами,
представляющими собой
электрические импульсы.
6. Логические операции
7. Инверсия (логическое отрицание - НЕ)
Инверсияделает
истинное
высказывание
ложным
и,
наоборот, ложное – истинным.
Обозначение: ¬А или A
Схема:
А
НЕ
A
Таблица истинности
А
A
1
0
0
1
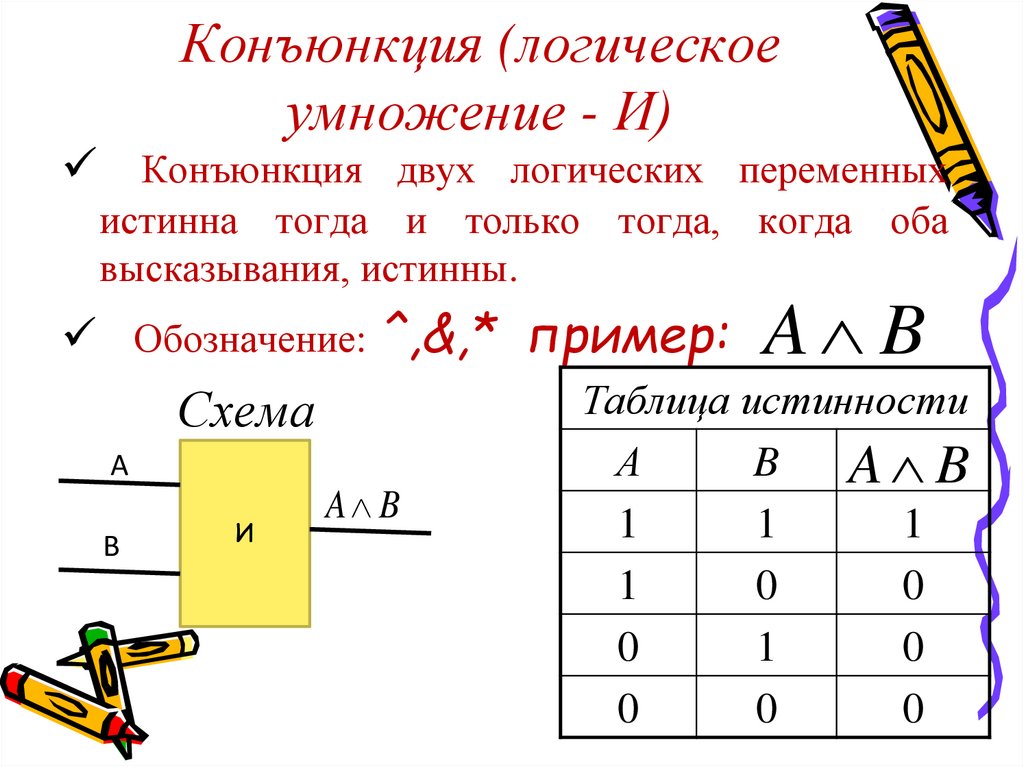
8. Конъюнкция (логическое умножение - И)
Конъюнкция двух логических переменныхистинна тогда и только тогда, когда оба
высказывания, истинны.
Обозначение: ^,&,* пример:
Схема
А
В
И
A B
A B
Таблица истинности
А
B
A B
1
1
1
1
0
0
0
1
0
0
0
0
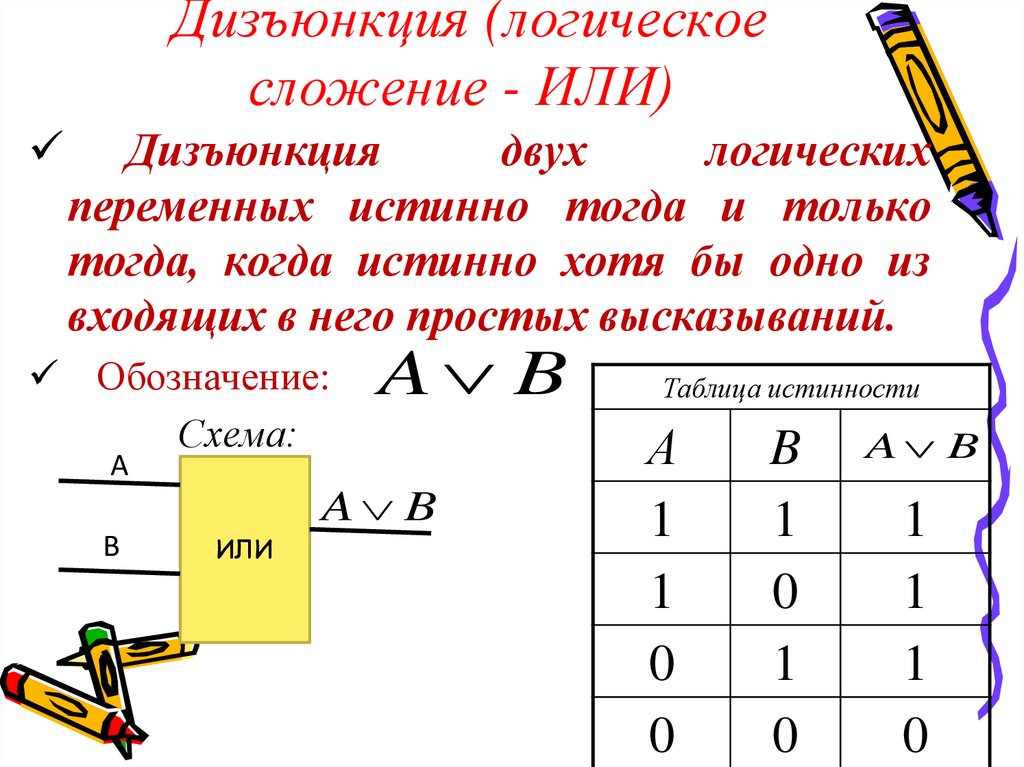
9. Дизъюнкция (логическое сложение - ИЛИ)
Дизъюнкциядвух
логических
переменных истинно тогда и только
тогда, когда истинно хотя бы одно из
входящих в него простых высказываний.
Обозначение:
Схема:
А
В
A B
A B
ИЛИ
Таблица истинности
А
1
1
0
0
B
1
0
1
0
A B
1
1
1
0
10. Импликация (логическое следование)
Импликация двух логических переменныхложна тогда и только тогда, когда из истинного
основания следует ложное следствие.
Таблица истинности
Обозначение: A B
А – условие
В - следствие
А
1
0
1
0
B
1
1
0
0
A B
1
1
0
1
11. Эквивалентность или тождество (логическое равенство)
Эквивалентность двух логических переменныхистинна тогда и только тогда, когда оба
высказывания одновременно либо ложны, либо
истинны.
Обозначение: ≡ , ↔ A B
Таблица истинности
А
1
1
0
0
B
1
0
1
0
A B
1
0
0
1
12. Приоритет выполнения логических операций
При вычислении значения логического выражения(формулы) логические операции вычисляются в
определенном порядке, согласно их приоритету:
1.инверсия,
2.конъюнкция,
3.дизъюнкция,
4.импликация и эквивалентность.
Операции
одного приоритета выполняются слева
направо. Для изменения порядка действий
используются скобки.
Пример
13. Пример
Дана формулаA B C А A
Определите порядок вычисления.
Порядок вычисления:
Инверсия – A
Конъюнкция – C А
Дизъюнкция – A B
Импликация – A B C А
Эквивалентность – A B C А A
14.
Дана функцияA
B
C
0
0
0
1
0
0
0
1
0
0
0
1
1
1
0
1
1
1
0
1
1
1
0
1
A B C А A
15.
Дана функцияA
B
C
1
0
0
0
0
0
0
0
1
0
1
1
1
1
1
1
1
0
0
1
0
1
0
1
В А А С A
16. Д.з.
Дана формула A С А В AОпределите порядок вычисления. Составить
таблицу истинности .
17.
Дана формулаА ^ ¬В
АVС≡А
Определите порядок вычисления. Составить
таблицу истинности .
18. Установите соответствие:
ИмпликацияУмножение
Дизъюнкция
Тождество
Инверсия
Следование
Эквивалентность
Сложение
Конъюнкция
Отрицание
19. Установите соответствие:
˅Умножение
≡
Тождество
˄
Следование
→
Сложение
Отрицание
̚

















 informatics
informatics








