Стойност на парите във времето

1.

СТОЙНОСТ НА ПАРИТЕ ВЪВ
ВРЕМЕТО
Паричните потоци, които
протичат в различни
моменти от времето са
несъпоставими по
номинална стойност.

2.

Факторите, които трябва да се
оценяват, са:
Инфлацията. При наличие на инфлация
се намалява реалната стойност на
паричната единица. Следователно, се
намалява и реалната стойност на
паричната сума.
Способността на капитала да нараства с
течение на времето като носи доход

3.

Изчисляване на нормата на
доходност в реално изражение
– r nom - норма на доходност в номинално
изражение;
– r real - норма на доходност в реално изражение;
– i - норма на инфлацията
1 rnom
1 rreal
1 i

4.

Бъдеща стойност /FV/
FV=S0 (1+r)n
където:
So - паричната сума в настоящия момент /в
началния момент/;
n - брой на периодите /най-често години/ до
момента от време, към който се изчислява
бъдещата стойност на паричната сума;
r - норма на доходност, която трябва да се получава
за един период от време /тя се прилага като
норма на олихвяване/

5.

Ако нормата на доходност, която трябва
да се получава за всеки период е
различна
FV= S0 (1+r1)(1+ r2)(1+r3)….(1+rn)
Където:
r1 – норма на доходност за първия период /първата година/;
r2- норма на доходност за втория период /втората година/;
r3 норма на доходност за третия период /третата година/;
rn норма на доходност за n-тия период /n - тата година/

6.

Бъдеща стойност на поредица от равни парични
потоци, които се получават в края на всеки
период /всяка година/
FV= S. FVAF(r;N)
1 r
FVAF(r, N)
N
r

7.

Бъдеща стойност на поредица от равни парични
потоци, които се получават в началото на всеки
период /всяка година/
FV= S. (FVAF(r;N+1) -1)

8.

Настояща стойност /PV/
Sn - паричната сума след n периода / години/;
n - брой на периодите /годините/ от настоящия момент до
момента от време, в който се получава или плаща
паричната сума;
r - норма на доходност, която трябва да се получава за един
период от време / тя се приема за норма на дисконтиране /
1
PV S n
(1 r ) n

9.

Ако годишната норма на доходност, която
трябва да се изисква е различна за всеки период
/всяка година/
r1 – норма на доходност за първия период /първата година/;
r2- норма на доходност за втория период / втората година/;
r3 норма на доходност за третия период /третата година/;
rn норма на доходност за п-тия период / n - тата година/
1
PV S n
(1 r1 )(1 r2 )(1 r3 )....(1 rn )

10.

Настояща стойност на поредица от равни
парични потоци, които се получават в
края на всеки период /всяка година/
PV = S x AF (r;N)

11.

Настояща стойност на поредица от равни
парични потоци, които се получават в
началото на всеки период /всяка година/
PV = S x (AF(r;N-1) +1)

12.

Как да определим нормата на доходност,
която следва да се получава от
използването на парите като капитал?
Анализите показват, че съществува
връзка между нормата на доходност и
риска при използването на парите като
капитал!
Инвестиционният риск се измерва с
разсейването на резултатите спрямо
средната очаквана стойност.
Показатели: дисперсия и стандартно
отклонение.

13.

Връзка между риск и доходност
/възвръщаемост/
Компоненти на инвестиционния риск
Специфичен риск - Това е частта от
общия риск, която се елиминира чрез
съставянето на инвестиционен портфейл
с разнообразни ценни книжа;
Системен риск - Това е частта от общия
риск, която не може да се елиминира чрез
съставянето на инвестиционен портфейл
от разнообразни ценни книжа.

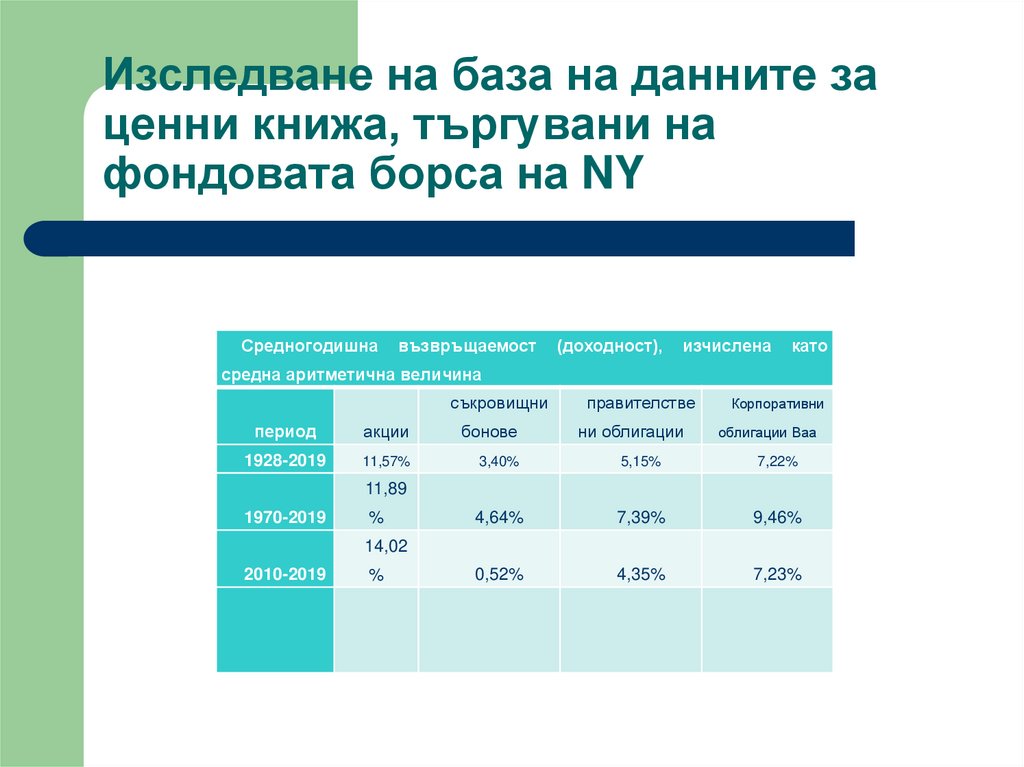
14.

Изследване на база на данните за
ценни книжа, търгувани на
фондовата борса на NY
Средногодишна
възвръщаемост
(доходност),
изчислена
като
средна аритметична величина
съкровищни
правителстве
ни облигации
Корпоративни
период
акции
бонове
1928-2019
11,57%
3,40%
5,15%
7,22%
4,64%
7,39%
9,46%
0,52%
4,35%
7,23%
облигации Ваа
11,89
1970-2019
%
14,02
2010-2019
%

15.

Продължение
Средногодишна
възвръщаемост
(доходност),
изчислена
като
средна геометрична величина
съкровищни
правителстве
Корпоративни
период
акции
бонове
ни облигации
1928-2019
9,71%
3,35%
4,88%
6,96%
4,58%
6,99%
9,18%
0,51%
4,13%
7,06%
облигации Ваа
10,51
1970-2019
%
13,44
2010-2019
%

16.

Връзка между възвръщаемост и
риск при инвестиране в
инвестиционен портфейл
При инвестиране в инвестиционен
портфейл се наблюдава ефектът на
диверсификацията.
Диверсификацията намалява риска, който
се поема от инвеститора.

17.

Възвръщаемостта на инвестиционния
портфейл зависи от два фактора:
възвръщаемост /доходност/ на ценните
книжа, включени в портфейла;
относителния дял на различните ценни книжа
в портфейла, определен по пазарните им
цени.

18.

Рискът на инвестиционния
портфейл зависи от три фактора:
-рискът на ценните книжа, включени в
портфейла;
-относителния дял на различните ценни
книжа, определен по пазарните им цени;
-взаимната корелация между
възвръщаемостта /доходността/ на
различните ценни книжа, включени в
портфейла.

19.

Ефект на диверсификацията
При инвестиране в инвестиционен
портфейл се намалява или може да бъде
изключен напълно специфичния риск, който
носят различните инвестиционни обекти.
В добре диверсифициран инвестиционен
портфейл всички инвестиционни обекти
участват във формирането на портфейлния
риск само със своя системен риск.

20.

Бета – коефициенти /показатели
за системен риск/
Cov(r; rm)
Бета- коефициентът = Var ( rm )

21.

Стойности на бета-коефициентите
Ако бета - коефициентът е 0, ценните книжа /инвестициите/
са безрискови, т.е. не носят системен риск;
Ако бета - коефициентът е 1, ценните книжа /инвестициите/
носят същата степен на системен риск, както пазарния
портфейл;
Ако бета - коефициентът е между 0 и 1, системният риск на
ценните книжа /инвестициите/ е нисък, по - малък от риска
на пазарния портфейл;
Ако бета - коефициентът е над 1, системният риск на
ценните книжа /инвестициите/ е висок, по - голям от риска
на пазарния портфейл.

22.

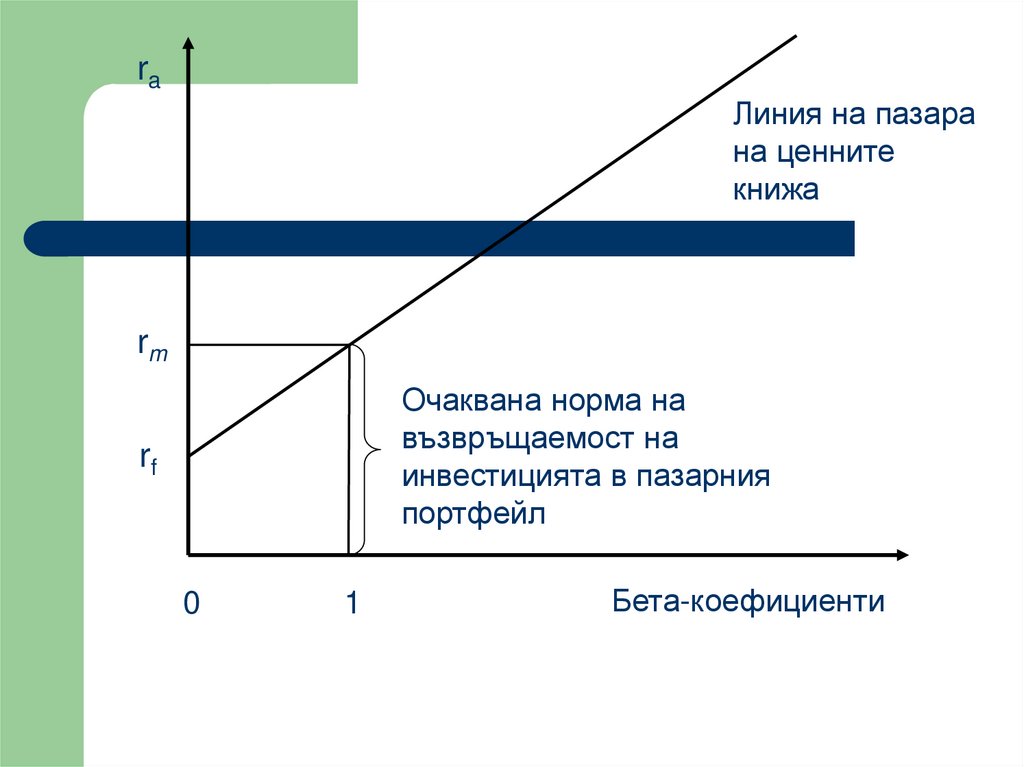
Връзка между системния риск и
нормата на възвръщаемост от
инвестициите
Връзката между системния риск и очакваната
норма на възвръщаемост се представя с Модела
за оценка на капиталовите активи (CAPM)
rа = rf + b(rm - rf)
където:
rа е нормата на възвръщаемост на а;
rf - безрисковата норма на доходност
(възвръщаемост);
rm - нормата на възвръщаемост на пазарния
портфейл.

23.

ra
Линия на пазара
на ценните
книжа
rm
Очаквана норма на
възвръщаемост на
инвестицията в пазарния
портфейл
rf
0
1
Бета-коефициенти

24.

Модел за оценка на капиталовите
активи – основни допускания:
Всички инвеститори вземат своите инвестиционни
решения като "рационални инвеститори";
Информацията за инвестиционните обекти се
разпространява свободно и е еднакво достъпна до всички
участници на капиталовия пазар;
Капиталовият пазар е добре развит, има достатъчен брой
участници и достатъчен обем обекти за търгуване;
Няма данъчно облагане на доходите от инвестициите;
Няма разходи по покупко-продажбите на ценни книжа;
Всеки участник може свободно без ограничения да
получава кредити и да предоставя кредити по един и същ
лихвен процент, равен на безрисковия.