Similar presentations:
Анализ деятельности сложных социально-экономических систем. Часть 4
1. Анализ деятельности сложных социально-экономических систем
Часть 4проф. Кривоножко В.Е.
2.
В этом разделе будем рассматривать производственные объекты, укоторых некоторые выходные параметры отрицательны. Пусть Io–
будет множество индексов векторов Yj, j = 1,…,n которые могут
принимать отрицательные значения.
Обозначим через J+ множество производственных объектов, у
которых X ≥ 0 и Y ≥ 0.
Переопределим множество производственных возможностей T на
основе постулатов 1-3 и множества J+.
T X , Y X X j j , Y Y j j , j 1, j 0
j J
j J
j J
T T E m r
(1)
(2)
В данной работе будем, в основном, рассматривать случай, где
производственный объект Zo = (Xo,Yo) имеет не только отрицательные
выходные компоненты, но и точка Xo не принадлежит множеству Tx –
проекции множества T на X-пространство. Определим два множества
Tx (Yo ) X xkj j xk , k 1, , m, yij j yio , i I o , j 1, j 0 , (3)
j J
j J
j J
T (Yo ) ( X , Y ) X Tx (Yo ), ( X , Y ) T
(4)
3.
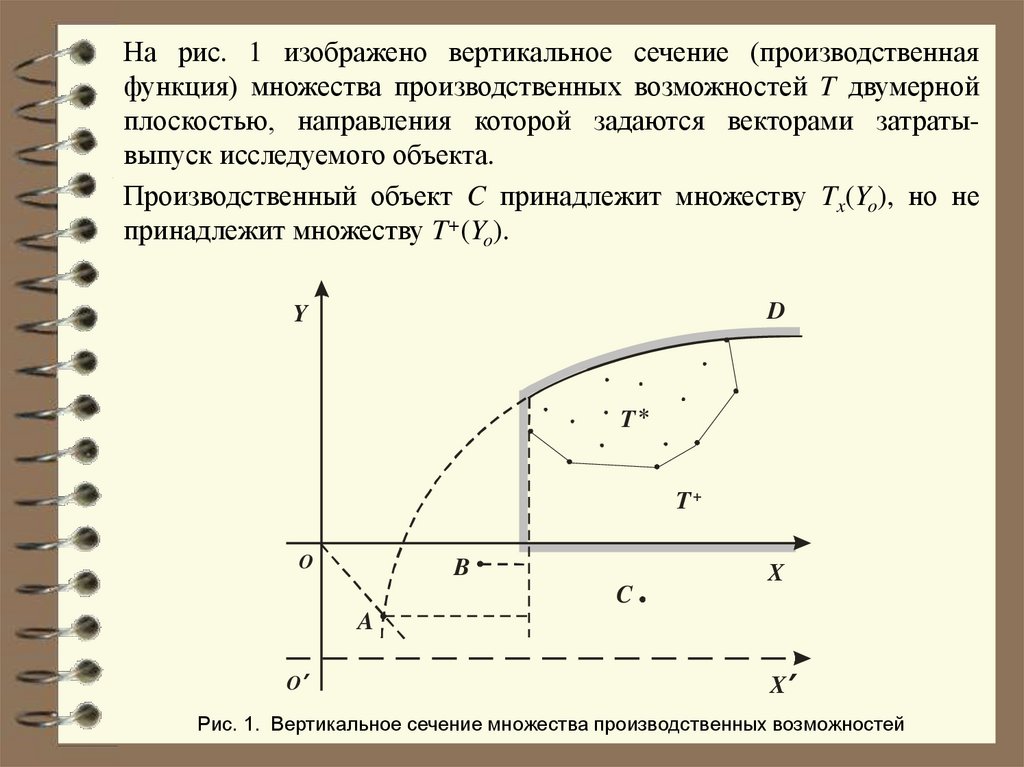
На рис. 1 изображено вертикальное сечение (производственнаяфункция) множества производственных возможностей T двумерной
плоскостью, направления которой задаются векторами затратывыпуск исследуемого объекта.
Производственный объект C принадлежит множеству Tx(Yo), но не
принадлежит множеству T+(Yo).
D
Y
T*
T+
O
B
C
X
A
O’
X’
Рис. 1. Вертикальное сечение множества производственных возможностей
4.
Теперь мы можем сформулировать нашу задачу. Для того, чтобыулучшить состояние объекта Zo необходимо перевести его в
множество T+(Yo) вдоль пути с минимальным расстоянием и при этом
сохранить положительные компоненты вектора Yo, по крайней мере,
на том же уровне.
Для наших целей, чтобы измерять расстояния, возьмем две нормы p =
∞ и p = 1. Напомним, что норма p = ∞ определяется следующим
образом:
(5)
Z max zi
i
т.е. берется максимальное значение по модулю среди компонент
вектора Z.
Алгоритм 1, приведенный ниже, позволяет нам находить
минимальное расстояние по бесконечной норме между объектом Zo и
множеством T+(Yo).
5.
Алгоритм 1.Шаг 1. Решаем задачу
min 1
X X d , d (1, ,1),
j J
j
j
o
1 1
1
Y j j Yo ,
(6)
j J
1, 0.
j J
Шаг 2. Решаем задачу
j
j
min 2
Yo 2 d 2 0,
0, i I o ,
di 2
1
,
i
I
o.
Шаг 3. Выбираем τ = max{τ1*, τ2*} в качестве минимального
расстояния по бесконечной норме между объектом Zo и множеством
T+(Yo) (4).
6.
Задача поиска минимального расстояния по бесконечной нормемежду точкой Xo и множеством Tx(Yo) может быть представлена в
виде
min
W , W Em,
(7)
( X o W ) Tx (Yo ).
Выберем произвольное направление d Em и ||d||∞ = 1. Рассмотрим
следующую оптимизационную задачу
min
X X d ,
j J
j
j
o
Y j j Yo ,
(8)
j J
1, 0.
j J
j
j
Лемма 1. Оптимальное значение функционала θ* в задаче (8) для
d = (1,…,1) определяет минимальное расстояние по бесконечной
норме от точки Xo до множества Tx(Yo).
Теорема 1. Величина τ, полученная из Алгоритма 1, минимизирует
расстояние по бесконечной норме между объектом (Xo,Yo) и
множеством T+ (Yo) .
7.
Перейдем к рассмотрению нормы p = 1 для измерения расстояниямежду точкой Zo и множеством T+(Yo). Напомним, что эта норма
определяется следующим образом
m r
Z 1 zi
i 1
(11)
т.е. берется сумма модулей компонент вектора Z.
Алгоритм 2, представленный ниже, позволяет находить минимальное
расстояние по единичной норме между точкой Zo = (Xo,Yo) и
множеством T+(Yo).
8.
Алгоритм 2.Шаг 1. Решаем задачу
m
min 1 w1k
ko
k 1
1
k
j
io
x x w , k 1, , m,
y y , i I ,
1, , w 0.
j J
kj
j
j J
j J
ij
j
o
j
(12)
1
k
Шаг 2. Решаем задачу
min 2 wi2
i I 0
(13)
yio wi2 0, i I o .
Шаг 3. Выбираем τ = τ1* + τ2* как минимальное расстояние по
единичной норме между точкой Zo и множеством T+(Yo).
9.
Используя (11), задачу поиска минимального расстояния поединичной норме между точкой Xo и множеством Tx(Yo) можно
представить в виде
m
min f wi
i 1
(14)
( X o W ) Tx (Yo ), W E m
Для того, чтобы упростить задачу (14) и раскрыть модуль,
представим пространство как сумму ортантов
где
E m E m E mj E Nm
(15)
E X X i ei k ek , i , k 0 ,
i L j
k L j
(16)
m
j
здесь ei, ek являются m-мерными единичными векторами с единицами
в позициях i и k, соответственно, и j = 1,…,N. Индексные множества
Lj+ и Lj– удовлетворяют условиям Lj+ ∩ Lj– = и Lj+ Lj– = L –
индексное множество пространства. Порядок нумерации ортантов
Ejm, j = 1,…,N, для наших целей не важен. Отметим только, что E1m =
E+m будет первым ортантом.
10.
Принимая во внимание (15), решение задачи (14) может быть сведенок решению семейства задач вида
Задача Pl , l = 1, … , N
m
min f l wi
i 1
x x w , i L ,
j J
ij
j
io
l
i
x
x
w
,
i
L
ij j il i
l ,
(17)
j J
y y , i I ,
j J
ij
j
o
io
1, , w 0.
j J
j
j
i
Обозначим через fl* оптимальное значение функционала задачи
Pl (17). Тогда минимальное значение по всем функционалам
f * = min fj* даст оптимальное значение задачи (14).
11.
Лемма 2. Для всех задач Pj, j = 1,…,N, имеющих решения,оптимальные значения функционалов подчиняются соотношениям f1*
fj*, j = 2,…,N.
Доказательство. Задача P1 из семейства (17) может быть записана в
виде
m
min f1 wi
i 1
при ограничениях
x x w , i 1, , m,
j J
ij
j
io
i
y y , i I ,
j J
ij
j
o
io
(18)
1, , w 0.
j J
j
j
i
Рассмотрим любую другую задачу из семейства (17), которая имеет
конечное решение.
12.
Сравнивая допустимые области задач DP1 и DPj, двойственных кзадачам P1 и Pj , соответственно, приходим к выводу, что допустимое
множество задачи DPj включает в себя допустимое множество задачи
DP1. Тогда
f1* f j*
А из этого следует, что
f1* f j*
Лемма 2 доказана.
Таким образом, для вычисления минимального расстояния по
единичной норме от точки Xo до множества Tx(Yo) достаточно решить
задачу (18).
Теорема 2. Величина τ, полученная из Алгоритма 2, минимизирует
расстояние по единичной норме между точкой (Xo,Yo) и множеством
T+(Yo) .
13.
Определимэмпирическое
возможностей T*
множество
производственных
T ( X , Y ) X X j j , Y Y j j , j 1, j 0 ,
j J
j J
j J
*
(19)
Рассмотрим задачу поиска минимального расстояния по бесконечной
или единичной норме между объектом Zo = (Xo,Yo) T* и множеством T*. Задача поиска минимального расстояния по бесконечной
норме между точкой (Xo,Yo) и множеством T* может быть записана в
виде
min
W ,
(20)
1
2
*
( X o W , Yo W ) T ,
W (W 1 ,W 2 ) E m r .
14.
Используя (19), задачу (20) можно переписать в видеmin
x x w , k 1, ... , m,
kj
j J
j
ko
1
k
y y w , i 1, ... , r ,
j J
ij
j
io
2
i
1, 0.
j J
j
j
w1k , k 1, ... , m,
wi2 , i 1, ... , r.
Итак, теперь мы можем сформулировать следующее утверждение.
(21)
15.
Теорема 3. Оптимальное значение функционала *, полученное изрешения задачи (21), минимизирует расстояние по бесконечной
норме между объектом (Xo,Yo) и множеством T*.
Доказательство. Действительно, ограничения задачи (21) записаны
в таком виде, что шар с центром в точке Zo = (Xo,Yo) должен
пересекаться с множеством T*, радиус шара по бесконечной норме
равен . Минимизация функционала задачи гарантирует, что
пересечение двух множеств произойдёт на границе того и другого
множества, тат как в противном случае радиус шара можно было бы
уменьшить.
Теорема доказана.
16.
Задача поиска минимального расстояния по единичной норме междуточкой (Xo,Yo) T+(Yo) и множеством T* может быть представлена в
виде
m r
min wi
i 1
( X o w , Yo w ) T .
1
2
(22)
*
Открывая модуль, используя (19) и полагая w1 = w1+ – w1–, w1+, w1–≥ 0,
w2 = w2+ – w2–, w2+, w2– ≥ 0, запишем задачу (22) в виде
m
r
min I ( w w ) ( wi2 wi2 ),
1
k
k 1
1
k
i 1
x x w w , k 1, ... , m,
j J
kj
j
ko
1
k
1
k
y y w w , i 1, ... , r ,
j J
ij
j
io
2
i
2
i
1,
j J
j
j 0, w1 , w1 , w2 , w2 0.
(23)
17.
Лемма 3. В оптимальном решении задачи (23) для любой парыпеременных (wk1+, wk1–), k = 1, …, m или (wi2+, wi2–) i = 1, …, r может
быть отлична от нуля только одна переменная из пары.
Доказательство. Как видно из условий задачи (23), добавление
положительной константы одновременно к двум переменным пары
не изменит допустимости решения. Однако, функционал задачи при
этом возрастёт. Отсюда следует, что в оптимальном решении может
быть отлична от нуля только одна из переменных пары.
Теорема 4. Оптимальное значение функционала задачи (23)
минимизирует расстояние по единичной норме между объектом
(Xo,Yo) и множеством T*.
18.
Теперь мы можем описать основные шаги процедуры по переводуобъекта из состояния с «отрицательной эффективностью» (некоторые
выходные параметры имеют отрицательное значение) на
эффективную гиперповерхность. Итак, пусть Zo = (Xo,Yo) T+(Yo).
1. Запускаем Алгоритм 1 или Алгоритм 2 для нахождения точки
(X o,Y o) множества T+(Yo), которая является ближайшей точкой
к точке (Xo,Yo)
по бесконечной или единичной норме.
Переводим объект (Xo,Yo) в позицию (X o,Y o) множества
T+(Yo).
Отметим,
что
множество
Tx(Yo)
можно
проинтерпретировать как область необходимых затрат для
объекта (Xo,Yo) для нормального функционирования.
2. Решаем задачу (21) или (23) для нахождения точки множества
T*, которая является ближайшей точкой к точке (X o,Y o) по
бесконечной или единичной норме. Переводим объект .
(X o,Y o) → (X o,Y o) T.
3. Используем стандартные методы методологии АСФ для
перевода объекта (X o,Y o) на эффективную гиперповерхность
множества производственных возможностей.
19.
Входные параметры:(вход 1) – суммарные активы, в тыс. руб.;
(вход 2) – процентные расходы, в тыс. руб.;
(вход 3) – прочие расходы в тыс. руб.
Выходные параметры:
(выход 1) – процентные доходы, в тыс. руб.;
(выход 2) – прочие доходы, в тыс. руб.;
(выход 3) – прибыль отчетного периода, в тыс. руб.,
где j = 1, …, 150, по числу исследуемых банков.
20.
Радиальный путь показывает, что каждый входной параметр долженбыть увеличен на 55%. А минимальное расстояние по единичной
норме дает, что только одна входная компонента должна увеличиться
на 55%. Вторая входная компонента должна увеличиться только на
38%. И третья компонента может вообще не меняться.
21.
Радиальный путь (θ = 1.55):x1j = 55 %, x1j = 968026 тыс. руб.;
x2j = 55 %, x2j = 4193 тыс. руб.;
x3j = 55 %, x3j = 16986 тыс. руб.
Минимальное расстояние по единичной норме:
x1j = 55 %, x1j = 968026 тыс. руб.;
x2j = 38 %, x2j = 2897 тыс.руб.;
x3j = 0 %,
x3j = 0 тыс. руб.
Приведенные цифры показывают, что минимальное расстояние по
единичной норме требует гораздо меньше расходов, чем
стандартный радиальный путь, для улучшения состояния банка.
22.
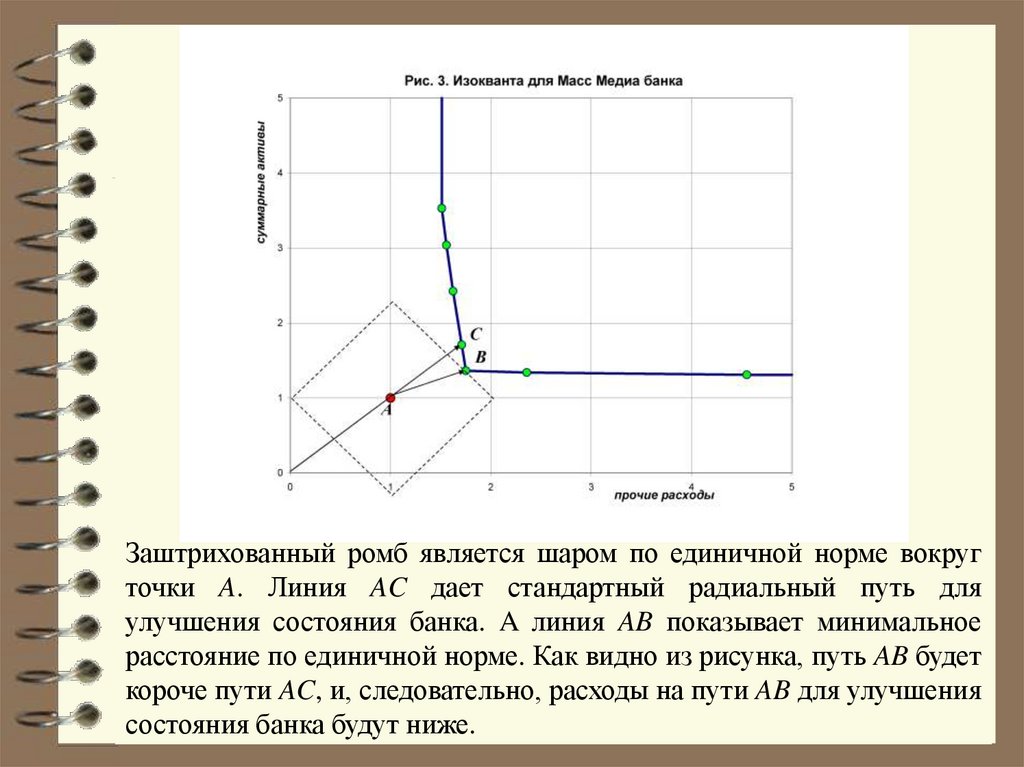
Заштрихованный ромб является шаром по единичной норме вокругточки A. Линия AC дает стандартный радиальный путь для
улучшения состояния банка. A линия AB показывает минимальное
расстояние по единичной норме. Как видно из рисунка, путь AB будет
короче пути AC, и, следовательно, расходы на пути AB для улучшения
состояния банка будут ниже.




















 mathematics
mathematics economics
economics








