Similar presentations:
ОГЭ-2023. Задание 16. Окружность, круг и их элементы
1.
Составила учитель математикиГринюк Любовь Викторовна
МАОУ Барыбинская СОШ
г. Домодедово
Московской области
2.
№1Радиус OB окружности с центром в точке O
пересекает хорду AC в точке D и перпендикулярен
ей. Найдите длину хорды AC, если BD = 1 см, а
радиус окружности равен 5 см.
Решение:
DO OB BD
DO АС - по условию
А
AOD прямоугольный
5
AD АО2 OD 2 = 3
1 В
АO CO r
О
с² = а² + b²D
AOD равнобедренный
Теорема Пифагора
АD DC
Квадрат гипотенузы равен
AC АD 2
сумме квадратов катетов.
С
16
6
3
10 х
х
3.
№2В треугольнике ABC угол C равен 90°, AC = 30 ,
BC =5√13. Найдите радиус окружности,
описанной около этого треугольника.
Решение:
Вписанный прямой угол опирается на диаметр окружности,
поэтому радиус окружности, описанной вокруг
прямоугольного треугольника, равен половине гипотенузы.
По теореме Пифагора
В
AВ
О
С
AВ 30 5 13
2
А
30
16
ВС 2 АС 2
1 7 , 5
3
10 х
х
АВ 1225 = 35
R 35 : 2
2
4.
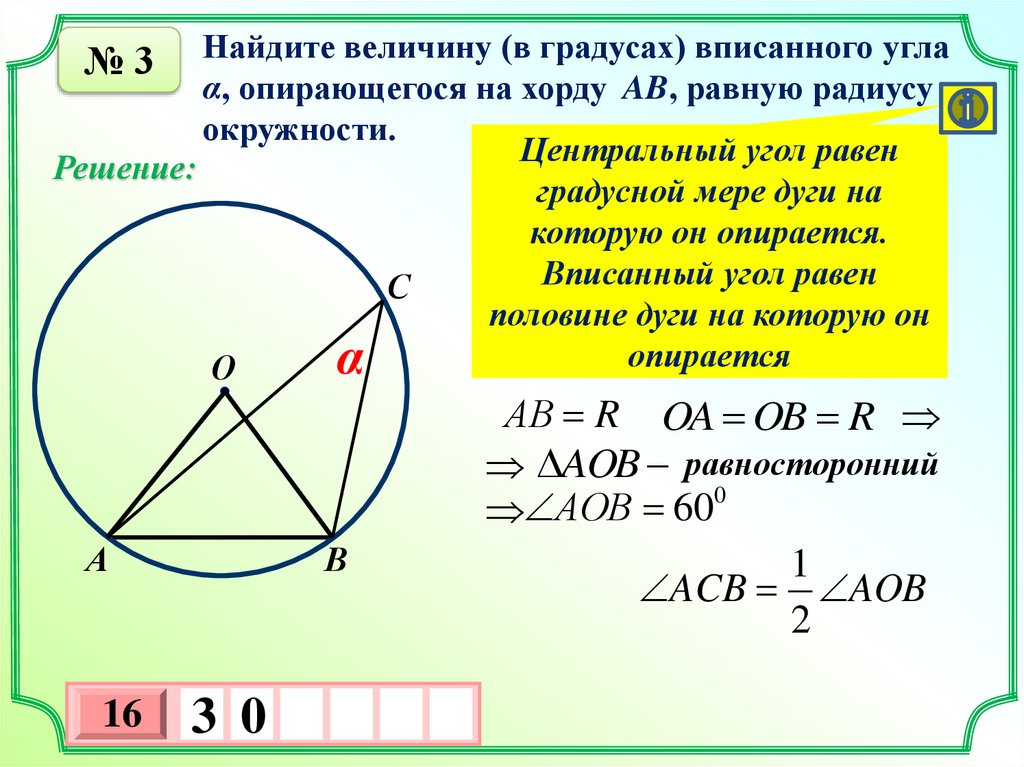
Найдите величину (в градусах) вписанного углаα, опирающегося на хорду AB, равную радиусу
окружности.
Центральный угол равен
Решение:
градусной мере дуги на
которую он опирается.
Вписанный угол равен
С
половине дуги на которую он
опирается
α
О
№3
А
16
АВ R OA OB R
AOB равносторонний
АOB 600
1
ACB AOB
2
В
3 0
3
10 х
х
5.
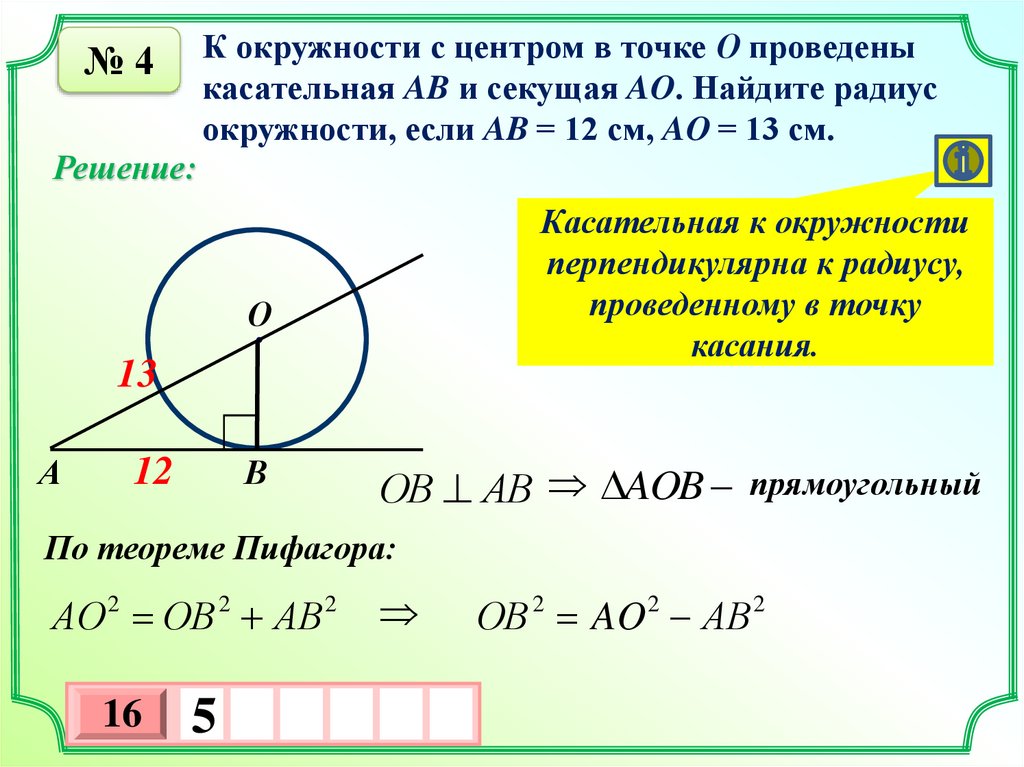
К окружности с центром в точке О проведеныкасательная AB и секущая AO. Найдите радиус
окружности, если AB = 12 см, AO = 13 см.
№4
Решение:
Касательная к окружности
перпендикулярна к радиусу,
проведенному в точку
касания.
О
13
А
В
12
ОВ АВ AOB прямоугольный
По теореме Пифагора:
АO 2 ОВ 2 АВ 2
5
х
16
3
10 х
ОB 2 AO 2 АB 2
6.
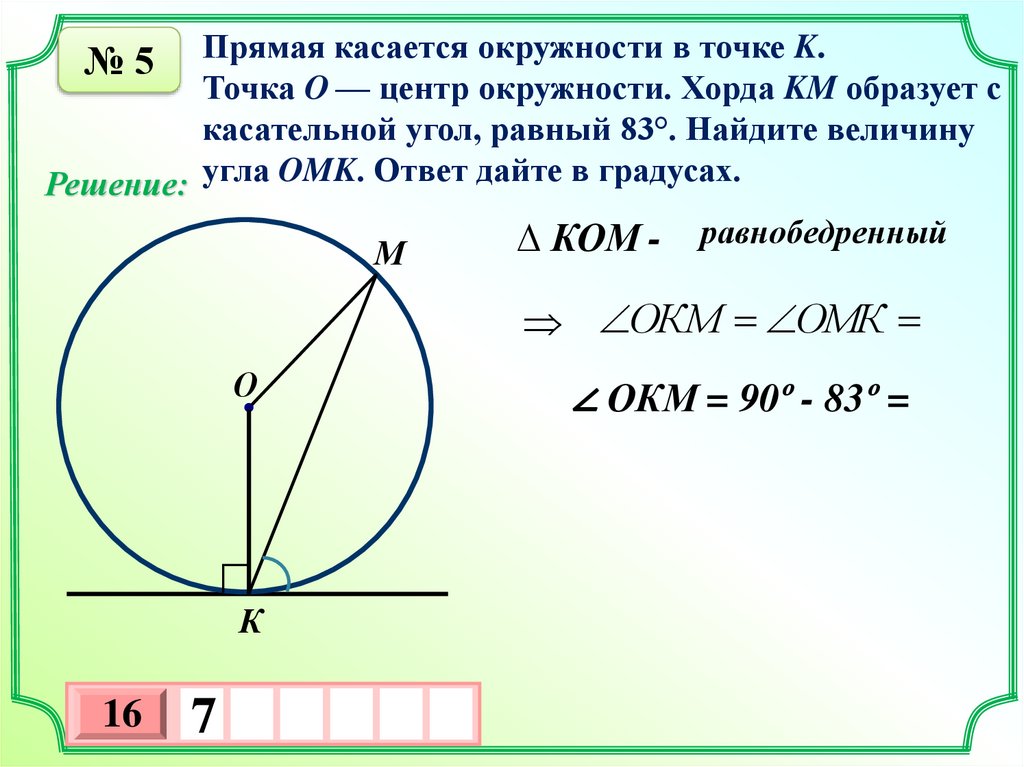
Прямая касается окружности в точке K.Точка O — центр окружности. Хорда KM образует с
касательной угол, равный 83°. Найдите величину
Решение: угла OMK. Ответ дайте в градусах.
№5
М
∆ КОМ - равнобедренный
ОКМ ОМК
О
∠ ОКМ = 90º - 83º =
∟
К
16
7
3
10 х
х
7.
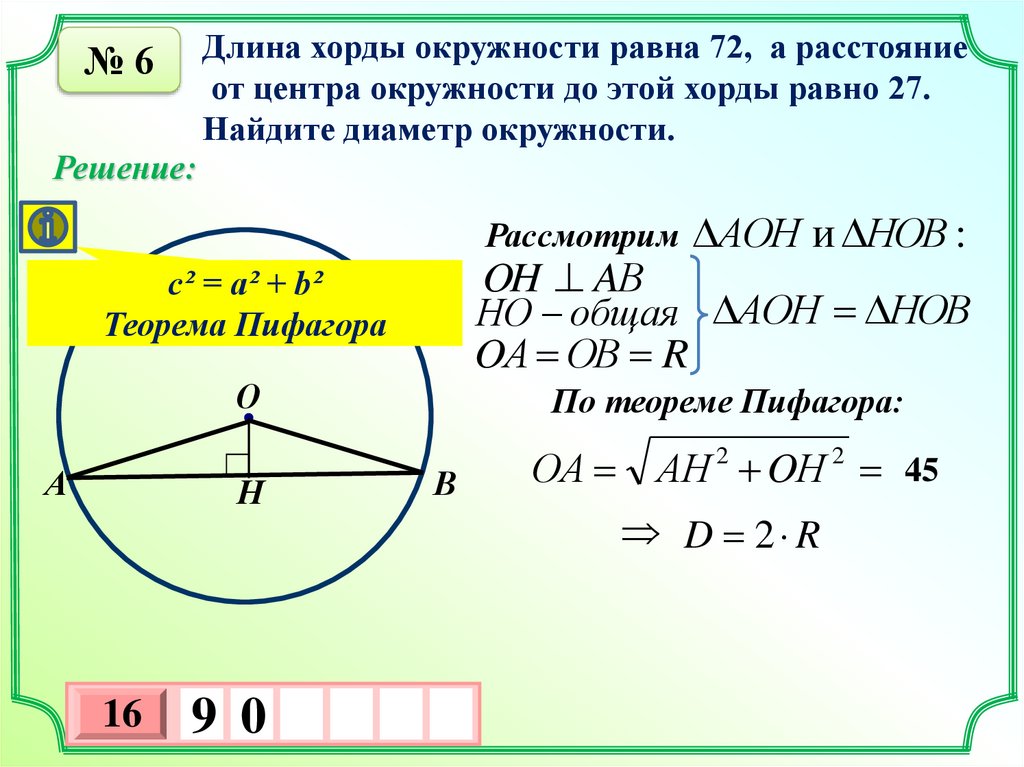
Длина хорды окружности равна 72, а расстояниеот центра окружности до этой хорды равно 27.
Найдите диаметр окружности.
№6
Решение:
Рассмотрим АОН и НOB :
с² = а² + b²
Теорема Пифагора
OH AВ
НO общая АОН НOB
OА ОВ R
О
По теореме Пифагора:
Н
ОA АН 2 OН 2 45
D 2 R
А
16
9 0
В
3
10 х
х
8.
К окружности с центром в точке О проведеныкасательная AB и секущая AO. Найдите радиус OD
окружности, если AB = 12 см, AO = 13 см.
№7
Решение:
В
Радиус окружности
перпендикулярен
касательной в точке касания
А
12
D
13
ОВ АВ
AOB прямоугольный
О
По теореме Пифагора:
АO 2 AВ 2 OВ 2
16
5
3
10 х
х
9.
№8Решение:
На отрезке AB выбрана точка C так, что AC = 75
и BC = 10. Построена окружность с центром A,
проходящая через C. Найдите длину отрезка
касательной, проведённой из точки B к этой окр-ти.
А 75
C 10 В
Касательная к окружности
перпендикулярна к радиусу,
проведенному в точку
касания.
AH ВH
ABH прямоугольный
?
H
По теореме Пифагора:
BH AВ 2 АH 2
16
4 0
3
10 х
х
AC CB АH 2
2
10.
Окружность радиусом 39 вписана в квадрат.Найдите площадь квадрата.
№9
Сторона квадрата равна
диаметру вписанной в него
окружности
Решение:
S 2R
R
2
О
16
S 2 39
2
6 0 8 4
3
10 х
х
11.
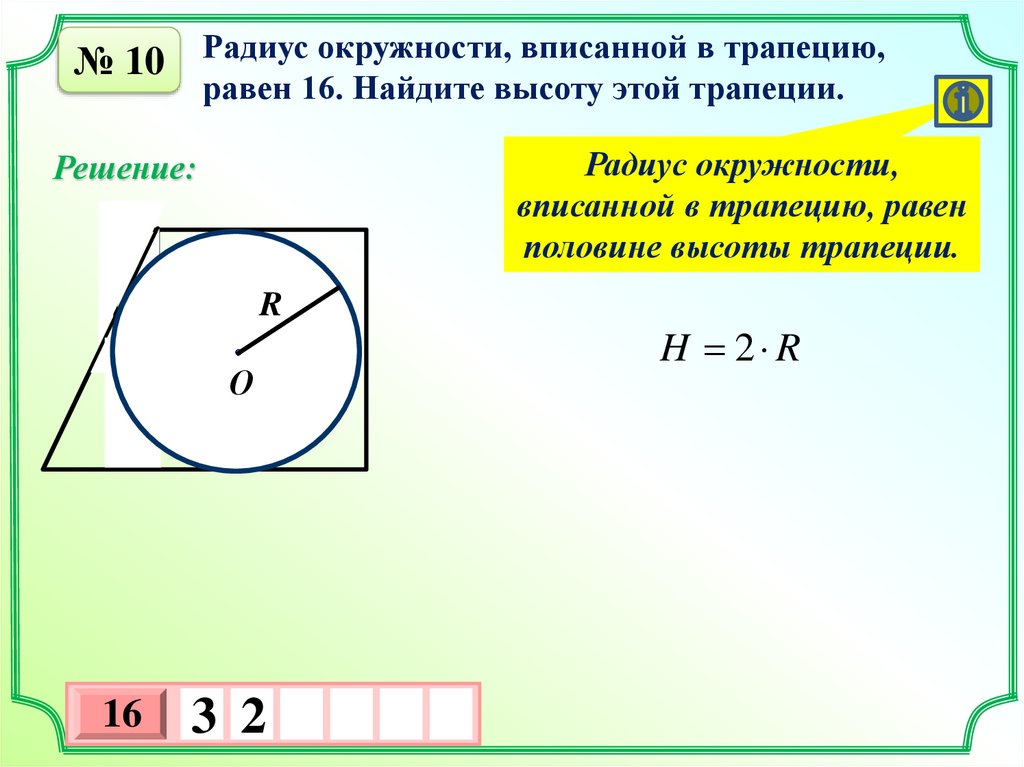
№ 10 Радиус окружности, вписанной в трапецию,равен 16. Найдите высоту этой трапеции.
Радиус окружности,
вписанной в трапецию, равен
половине высоты трапеции.
Решение:
R
H 2 R
О
16
3 2
3
10 х
х
12.
№ 11 Радиус вписанной в квадрат окружности равен. Найдите диагональ этого квадрата.
Решение:
В
С
R
a
О
A
D
16
8
3
10 х
х
Радиус вписанной в квадрат
окружности вдвое меньше
её стороны.
a 2 R
a 4 2
13.
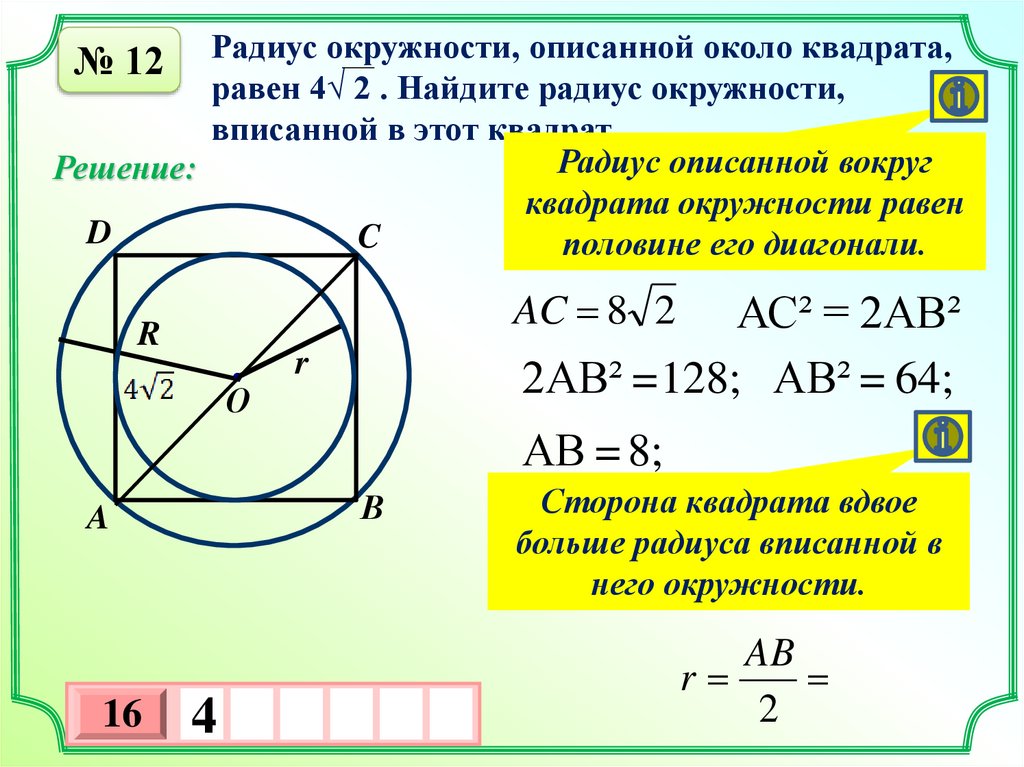
Радиус окружности, описанной около квадрата,равен 4√ 2 . Найдите радиус окружности,
вписанной в этот квадрат.
Радиус описанной вокруг
Решение:
квадрата окружности равен
D
C
половине его диагонали.
№ 12
AC 8 2
R
АС² = 2АВ²
2АВ² =128; АВ² = 64;
r
О
АВ = 8;
16
Сторона квадрата вдвое
больше радиуса вписанной в
него окружности.
В
A
4
3
10 х
х
AB
r
2
14.
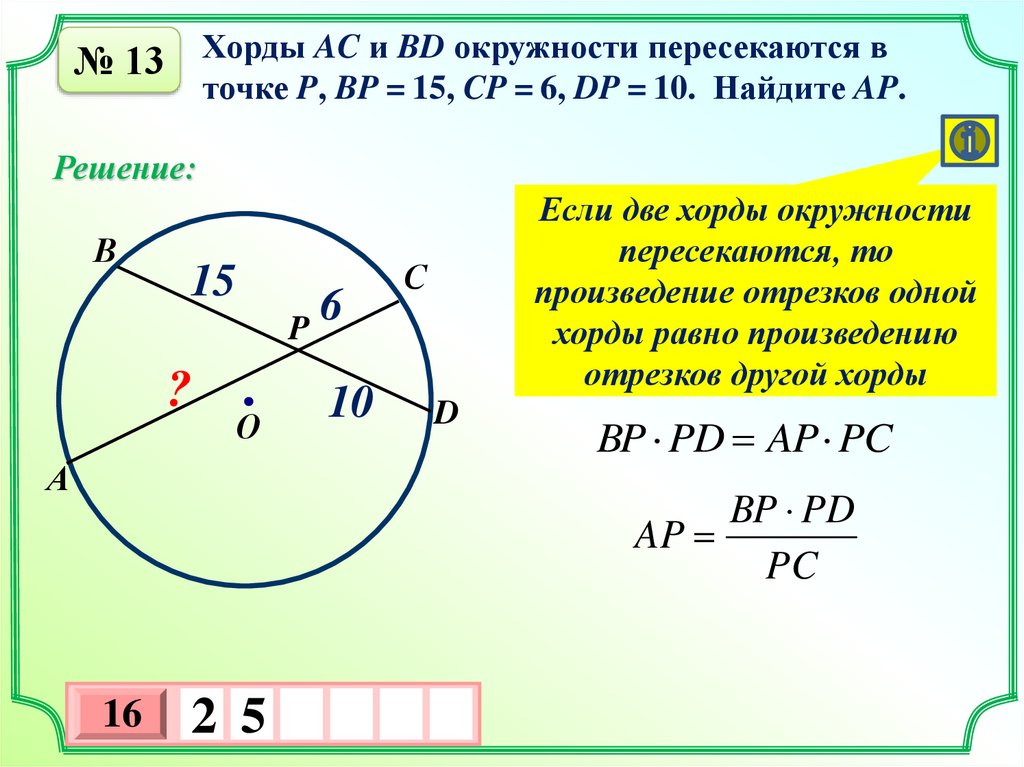
№ 13 Хорды AC и BD окружности пересекаются вточке P, BP = 15, CP = 6, DP = 10. Найдите AP.
Решение:
В
15
P
?
О
Если две хорды окружности
пересекаются, то
произведение отрезков одной
хорды равно произведению
отрезков другой хорды
С
6
10
D
А
BP PD AP PC
BP PD
AP
PC
16
2 5
3
10 х
х
15.
№ 14 На окружности отмечены точки A и B так, чтоменьшая дуга AB равна 72°. Прямая BC касается
окружности в точке B так, что угол ABC острый.
Решение: Найдите угол ABC. Ответ дайте в градусах.
Центральный угол равен
градусной мере дуги на
которую он опирается
О
А
AOB равнобедренный
72º
?
С
В
AOB центральный
0
АOB 72
1800 720
ОВA ОAB
2
АBС 90 54
0
16
3 6
3
10 х
х
0
16.
№ 15 Через точку A, лежащую вне окружности,проведены две прямые. Одна прямая касается окрти в точке K. Другая прямая пересекает окр-ть в
Решение: точках B и C, причём AB = 2, AC = 8. Найдите AK.
С
Если из точки, лежащей вне
окружности, проведены
касательная и секущая, то
квадрат длины касательной
равен произведению секущей
на ее внешнюю часть
8
О
В
2
А
АК 2 АВ АС
К
16
4
AК АВ АС
3
10 х
х
17.
№ 16Решение:
Сторона равностороннего треугольника равна
. Найдите радиус окружности,
вписанной в этот треугольник.
Центр вписанной
окружности находится в
точке пересечения
биссектрис треугольника.
С
АСН : АС 2 АН 2 СН 2
О
СН АС 2 АН 2 3
Н
А
16
1
В
3
10 х
х
Медианы точкой пересечения
делятся в отношении 2:1
СН
ОН
3
18.
№ 17 Радиус окружности, вписанной в равностороннийтреугольника равен
. Найдите длину
стороны этого треугольника..
Решение:
С
∆АВС -
АСН : СН =
∠ А = 60º
a
О
r
∟
А
В
Н
16
равносторонний
1 2
3
10 х
х
АС =











 mathematics
mathematics








