Similar presentations:
Статически определимые системы. Часть 1
1.
Часть 1. Статически определимые системы1.1. Определение внутренних сил
Общие принципы определения внутренних сил
в статически определимых системах
Для определения внутренних сил N , Q , M во
всех статически определимых системах можно
использовать способ сечений. Суть данного способа состоит в следующем:
а) в интересующем месте конструкции проводится сквозное сечение;
б) составляются уравнения равновесия для
части конструкции, расположенной с какой-либо
стороны от проведенного сечения (внутренние
2.
силы N , Q , M в сечении изображаются при этом вположительных направлениях);
в) из уравнений равновесия определяются внутренние силы N , Q , M в сечении.
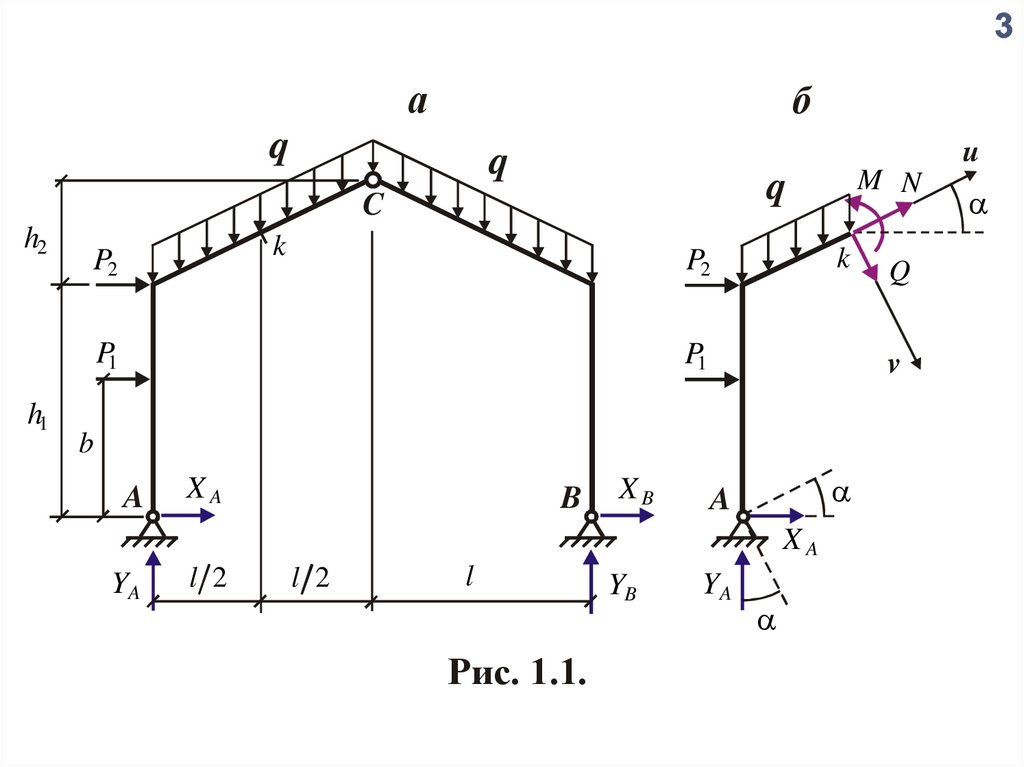
Пример: Определить внутренние силы N , Q , M
в сечении k рамы (рис. 1.1а).
Составляем три уравнения равновесия для
части рамы, расположенной слева от сечения k
(рис. 1.1б):
U ( X A P1 P2 ) cos (Y A ql 2) sin N 0;
V ( X A P1 P2 ) sin (Y A ql 2) cos Q 0;
M k X A ( h1 h2 2) Y A l 2
P1 ( h1 h2 2 b) P2 h2 2 ql 2 8 M 0.
3.
аб
q
u
q
C
h2
k
P2
k
P2
P1
h1
M N
q
P1
v
b
A
XA
B
XB
A
XA
YA
l 2
l 2
l
Рис. 1.1.
YB
Q
YA
4.
Из этих уравнений получаем N , Q , M в сечении k(реакции X A , Y A считаются известными):
N ( X A P1 P2 ) cos (Y A ql 2) sin ;
Q ( X A P1 P2 ) sin (Y A ql 2) cos ;
M X A ( h1 h2 2) Y A l 2 P1 ( h1
h2 2 b ) P2 h2 2 ql 2 8 .
Анализ полученных выше выражений позволяет сформулировать правила знаков для прямого
получения N , Q , M от действия внешних сил (без
составления уравнений равновесия отсеченной
части конструкции):
5.
а) если сила растягивает стержень в заданномсечении, то она дает в нем N >0;
б) если сила стремится вращать часть конструкции вокруг сечения по ходу часовой стрелки,
то она дает в нем Q >0;
в) если сила растягивает сечение с нижней или с
правой стороны, то она дает в нем M >0.
Необходимо отметить, что при расчете конструкции внутренние силы N , Q , M определяются
обычно не в одном сечении (как в данном примере), а находится распределение их по длине
стержней конструкции в виде эпюр N , Q , M .
6.
Расчет статически определимых балокВ поперечных сечениях балок от нагрузки перпендикулярной их оси возникают поперечная сила Q и изгибающий момент M . Внешние и внутренние силы в балках находятся в определенных
зависимостях. Рассмотрим произвольную балку
(рис. 1.2) и составим уравнения равновесия бесконечно малого элемента dx данной балки.
q q( x )
y
q
x
0
x
M
dx
Q
Рис. 1.2.
dx
k M dM
Q dQ
7.
Y Q q( x )dx Q dQ 0;dx
M k M Qdx q( x )dx M dM 0.
2
Из этих уравнений получаем две зависимости:
dQ
dM
q( x );
Q.
dx
dx
Данные зависимости позволяют определять характер эпюр Q , M на участках балки и проверять
правильность построения данных эпюр.
Частные случаи
1. Участок балки с q( x ) 0 : Q const , M линейно зависит от x (рис. 1.3а).
2. Участок балки с q const : Q линейно убывает
(при направлении q вниз), а M меняется по зако-
8.
ну квадратной параболы (рис. 1.3б). Если в каком-либо сечении участка Q 0, то в этом сечении эпюра M имеет экстремум ( dM dx 0 ).а
б q const
q 0
l 2
+
Q
l 2
+
Q
M
Рис. 1.3.
M
ql 2 8
Экстремум
9.
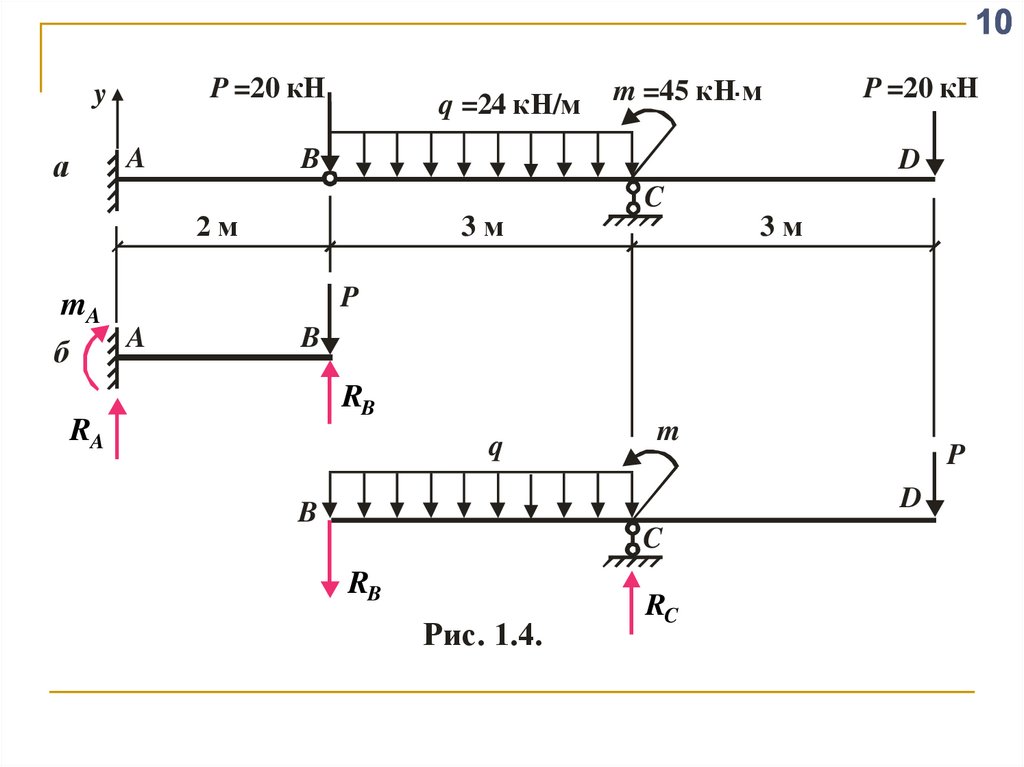
Пример: дана статически определимая балка суказанными размерами и нагрузкой (рис. 1.4а).
Построить эпюры Q, M .
1. Разделяем балку на две части по шарниру B
(рис. 1.4б) и составляем уравнения равновесия
для каждой части, из которых находятся реакции
опор и силы взаимодействия между этими частями.
Для части BCD:
M C RB 3 q 3 1,5 m P 3 0; RB 31кН;
Y RB q 3 RC P 0; RC 61кН.
Для части AB:
Y R A P RB 0; R A 51кН;
M A m A P 2 RB 2 0; m A 102кН м.
10.
P =20 кНy
A
а
q =24 кН/м
B
P =20 кН
D
2м
mA
A
б
m =45 кН.м
3м
C
3м
P
B
RB
RA
q
m
P
D
B
C
RB
Рис. 1.4.
RC
11.
2. Определяем Q и M на каждом участке балкиНаправление движения по каждому участку определяется расположением букв в обозначении
участка: первая буква - начало участка, вторая конец участка. Знаки Q и M от внешних сил определяются по изложенным ранее правилам.
Участок AB:
Q R A 51 кН; M A m A 102 кН м; M B 0.
Участок BC:
QB RB 31 кН; QС RB q 3 41 кН;
M B 0; M C RB 3 q 3 1,5 15 кН м.
Участок DC:
Q P 20 кН; M D 0; M C P 3 60 кН м.
12.
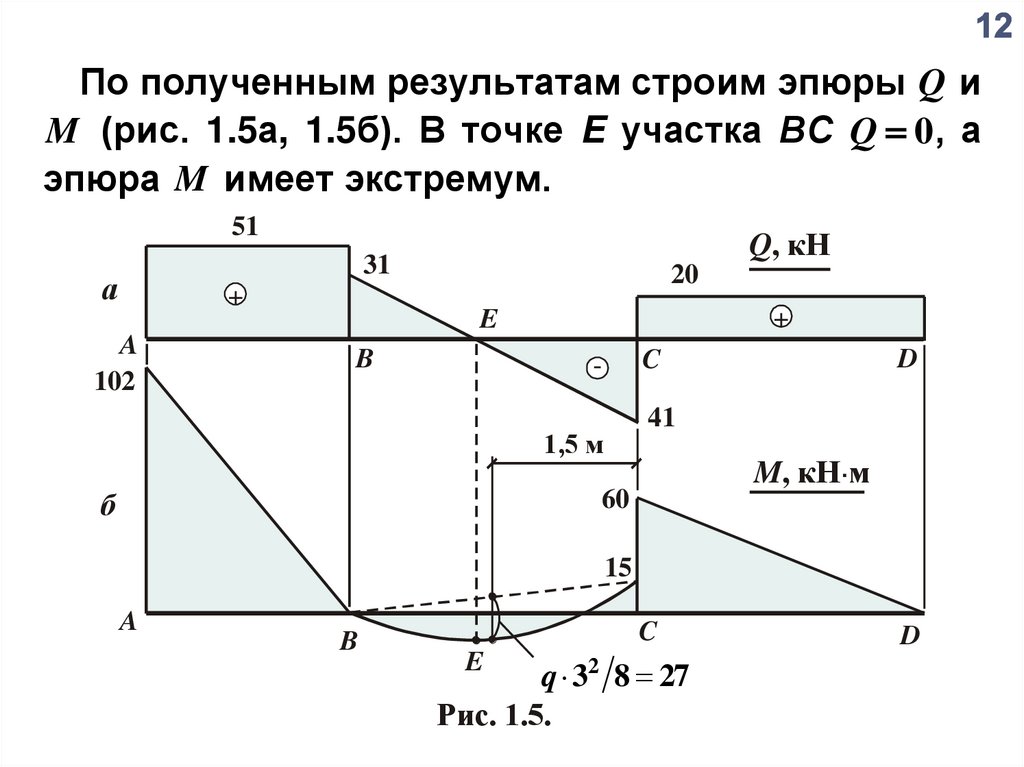
По полученным результатам строим эпюры Q иM (рис. 1.5а, 1.5б). В точке E участка ВС Q 0, а
эпюра M имеет экстремум.
51
Q, кН
31
а
+
A
102
20
+
E
B
41
1,5 м
б
D
C
-
M, кН.м
60
15
A
B
C
E
q 32 8 27
Рис. 1.5.
D









 mechanics
mechanics








