Методы нахождения корней уравнения на заданном промежутке при помощи программирования на языке С++

1.

МЕТОДЫ НАХОЖДЕНИЯ
КОРНЕЙ УРАВНЕНИЯ НА
ЗАДАННОМ ПРОМЕЖУТКЕ
ВЫПОЛНИЛИ:
МЕЩЕРЯКОВ АЛЕКСЕЙ
ЩЕТИНИНА АННА

2.

ЦЕЛЬ ПРОЕКТА
• Найти два способа нахождения корней уравнения при помощи программирования на
языке С++ для того, чтобы продемонстрировать полученные навыки.
ПЛАН ВЫПОЛНЕНИЯ
• Исследовать методы нахождения корней и определить два из них, которыми мы будем
пользоваться
• Проанализировать ход решения и продумать, как его можно преобразовать в
программный код
• Написать код, отладить его, и проверить как он работает с различными примерами

3.

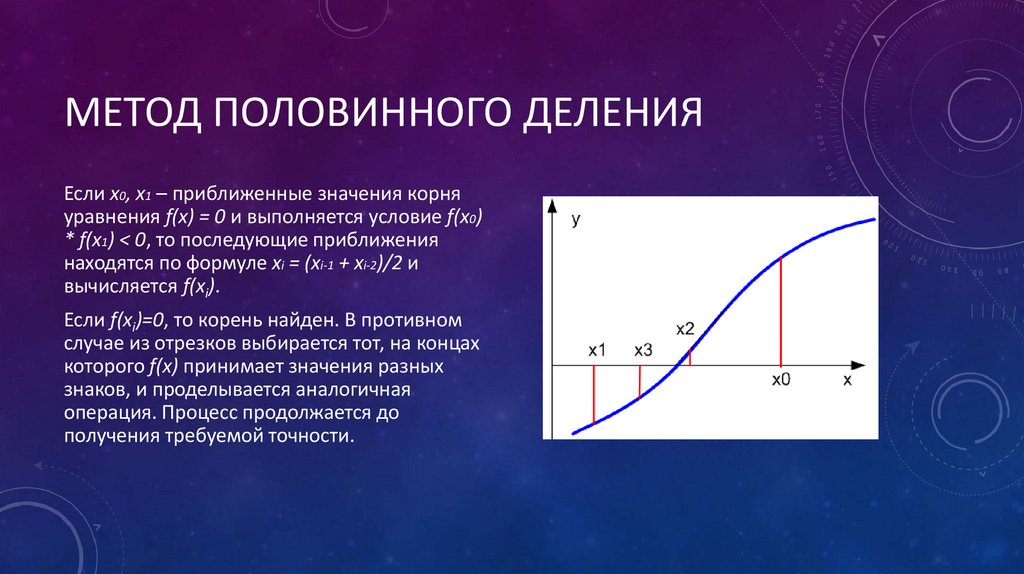
МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
Если х0, х1 – приближенные значения корня
уравнения f(x) = 0 и выполняется условие f(x0)
* f(x1) < 0, то последующие приближения
находятся по формуле xi = (xi-1 + xi-2)/2 и
вычисляется f(xi).
Если f(xi)=0, то корень найден. В противном
случае из отрезков выбирается тот, на концах
которого f(x) принимает значения разных
знаков, и проделывается аналогичная
операция. Процесс продолжается до
получения требуемой точности.

4.

5.

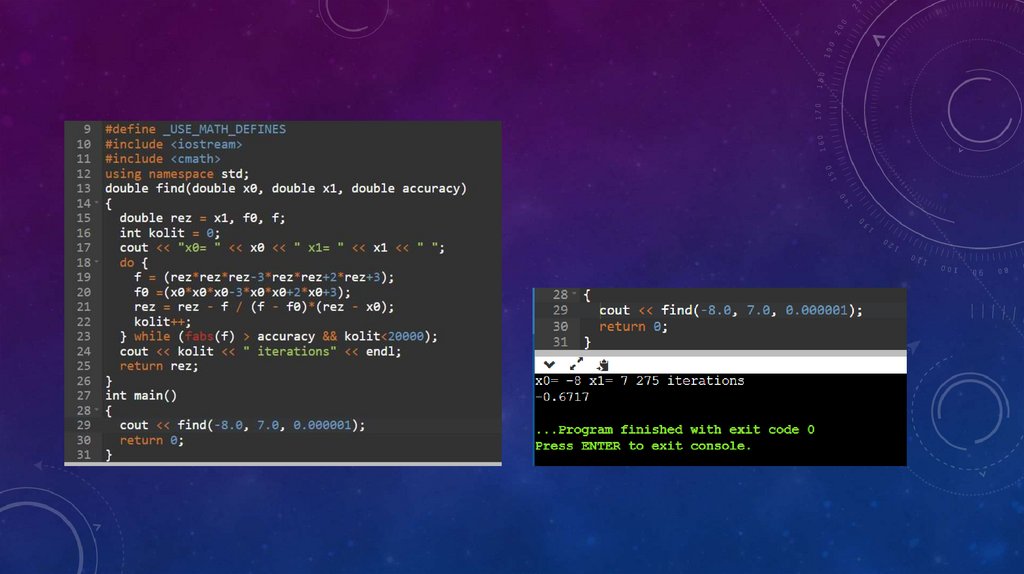
МЕТОД ХОРД
Если х0, х1 – приближенные значения корня
уравнения f(x) = 0 и выполняется условие f(x0)
* f(x1) < 0, то последующие приближения
находятся по формуле:
Методом хорд называют также метод, при
котором один из концов отрезка закреплен,
т.е. вычисление приближения корня
уравнения f(x) = 0 производят по формуле:

6.

7.

ПОДВЕДЕНИЕ ИТОГОВ
Мы нашли два самых простых и оптимальных метода нахождения корней уравнения на
заданном промежутке и написали код на языке С++, с помощью которого можно быстро
выполнить все необходимые расчеты.
В процессе разработки и создания нашего проекта мы намного лучше разобрались на
практике в данном языке программирования и продемонстрировали полученные нами на
курсах знания.