Similar presentations:
Documentclass[fullscreen=true,
1.
\documentclass[fullscreen=true,bookmarks=false]{beamer}
2.
\usepackage[utf8]{inputenc}3.
\usepackage[english,russian]{babel}4.
\usepackage{xcolor}5.
\usepackage{graphicx}6.
%\usepackage{Warsaw}7.
\newtheorem{thm}{Теорема}8.
\newtheorem{cor}{Следствие}9.
\newtheorem{lm}{Лемма}10.
\newtheorem{rmk}{Замечание}11.
\newtheorem{ex}{Пример}12.
\newtheorem{opr}{Определение}
13.
\newtheorem{ob}{Обозначение}14.
\title{Решеткиквазимногообразий
РіСЂСѓРїРї}
15.
\author{Мамаев К.А.}16.
\institute{Алтайскийгосударственный
университет,\\ Барнаул,
Р РѕСЃСЃРёСЏ}
17.
\date{Мой выбор – НАУКА!\\ 19 - 29 Апреля 2023}
18.
\begin{document}19.
\begin{frame}20.
\titlepage21.
\end{frame}22.
\begin{frame}{Основныеопределения и
теоремы}
23.
\begin{block}{Определение 1.}24.
$t_1$($x_1$,...,$x_n$)=$t_2$($x_1$,...,$x_n$), РіРґРµ $t_1$($x_1$,...,$x_n$),
$t_2$($x_1$,...,$x_n$) - групповые
слова в переменных из
алфавита $\{ x_1,...,x_n\}$ ,
называется тождеством.
25.
\end{block}26.
\begin{block}{Определение 2.}27.
$t_1$,$t`_1$,...,$t_k$,$t`_k$,t,t` групповые слова впеременных из
алфавита $\{ x_1,...,x_n\}$,
называется
квазитождеством.
28.
\end{block}29.
\begin{block}{Определение 3.}30.
существует множествотождеств $\Sigma$ таких,
что G $\in$ $\mathcal{M}$ тогда и
только тогда, когда все
формулы из $\Sigma$
истинны в G.
31.
\end{block}32.
\end{frame}33.
\begin{frame}{Основныеопределения и
теоремы}
34.
\begin{block}{Определение 4.}35.
если существуетмножество
квазитождеств $\Sigma$
$\mid$ G $\in$ $\mathcal{M}$ тогда и
только тогда, когда все
формулы из $\Sigma$
истинны в G.
36.
\end{block}37.
\begin{block}{Определение 5.}38.
$\in$ S положено a $\leq$ b,должны выполняться: \\
1) a $\leq$ a, (закон
рефлексивности) \\ 2)
если a $\leq$ b и b $\leq$ c , то а
$\leq$ c, (закон
транзитивности) \\ 3)
если a $\leq$ b и b $\leq$ a то a=b.
(закон
антисимметричности).
39.
\end{block}40.
\begin{block}{Определение 6.}41.
решеткой, если длялюбых a,b $\in$ S есть
точная верхняя
грань и точная
нижняя грань (a $\vee$ b, a
$\wedge$ b).
42.
\end{block}43.
\end{frame}44.
\begin{frame}{Основныеопределения и
теоремы}
45.
\begin{block}{Теорема 1.}46.
($\forall$x) ($\forall$y) (xy=yx) \\2)$\Psi_{p^{n+1}}$ = ($\forall$x)($x^{p^{n+1}}$
= 1 $\rightarrow$ $x^{p^n}$=1), \\ РіРґРµ p,n
(p $\in$ P) -- всевозможные
числа такие, что $p^n$
$\in$$\mathcal{X}$($\mathcal{M}$).
Если $\mathcal{X}$($\mathcal{M}$) =
$\varnothing$, то $\mathcal{M}$
совпадает с классом
абелевых групп.
47.
\end{block}48.
\begin{block}{Теорема 2.}49.
$\mathcal{M}$ являетсямногообразием и
задается тождествами:
\\$\Psi$ = ($\forall$x)($\forall$y) (xy=yx),
\\$\Psi_m$ = ($\forall$x) ($x^m$=1), \\ РіРґРµ
m -- произведение всех
чисел из
$\mathcal{X}$($\mathcal{M}$).
50.
\end{block}51.
\end{frame}52.
\begin{frame}{Основныеопределения и
теоремы}
53.
\begin{block}{Теорема 3.}54.
простых чисел. Тогдавсякая циклическая pгруппа из
квазимногообразий qS, qS
$\cup$ $\{Z\}$ изоморфна
подходящей
подгруппе некоторой
РіСЂСѓРїРїРµ РёР· S.
55.
\end{block}56.
\begin{block}{Построениерешеток }
57.
1. Квазимногообразиеq($Z_{75}$,Z).
58.
\end{block}59.
\begin{block}{Теорема 4.}60.
Решетка $L_q(q(Z_{75},Z))$ - эторешетка,
изображенная на рис. 1.
61.
\end{block}62.
Доказательство.63.
Алгоритм построениярешетки $L_q(q(Z_{75},Z))$.
64.
из этогоквазимногообразия,
воспользовавшись
теоремой 3. Для этого
заметим, что
$q(Z_{75},Z)=q(Z_{25},Z_{3},Z) $.
65.
2) Вычисляем $\chi (q(Z_{75},Z))$.66.
\end{frame}67.
\begin{frame}{Построениерешеток}
68.
которыми могутпорождаться
подквазимногообразия
данного
квазимногообразия.
69.
этом иногда добавляемк циклическим pгруппам ранее
найденные списки pгрупп.
70.
Видим, что71.
1) Цикл(q($Z_{75}$))=$\{E,Z_3,Z_5,Z_{25} \}$
72.
2) $\chi (q(Z_{75},Z))$=$\{1,3,25 \}$73.
получаем, чтоквазимногообразие
q($Z_{75}$,Z) задается
следующим множеством
квазитождеств:
74.
($\forall$x)($\forall$y) (xy=yx)75.
($\forall$x)($x^9=1 \rightarrow x^3=1)$76.
($\forall$x)($x^{125}=1 \rightarrowx^{25}=1)$
77.
($\forall$p $\neq$ 5)($\forall$p $\neq$ 3)($\forall$x)($x^p=1 \rightarrow x=1$)
78.
\end{frame}79.
\begin{frame}{Построениерешеток}
80.
Цикл($\mathcal{N}$) дляподквазимногообразий
$\mathcal{N}$
квазимногообразия
q($Z_{75}$,Z).
81.
3)Цикл($\mathcal{N}_1$) = $\{E\}$,82.
Цикл($\mathcal{N}_2$) = $\{E,Z_3\}$,83.
Цикл($\mathcal{N}_3$) = $\{E,Z_5\}$,84.
Цикл($\mathcal{N}_4$) =$\{E,Z_3,Z_5\}$,
85.
Цикл($\mathcal{N}_5$) =$\{E,Z_5,Z_{25}\}$,
86.
Цикл($\mathcal{N}_6$) =$\{E,Z_3,Z_5,Z_{25}\}$.
87.
Получаем следующиеподквазимногообразия
квазимногообразия
q($Z_{75}$,Z):
88.
$\mathcal{N}_1$=qE,89.
$\mathcal{N}_2$=q$Z_3$,90.
$\mathcal{N}_3$=q$Z_5$,91.
$\mathcal{N}_4$=q$\{Z_3,Z_5 \}$,92.
$\mathcal{N}_5$=q$Z_{25}$,93.
$\mathcal{N}_6$=q$Z_{75}$,94.
$\mathcal{N}_7$=qZ,95.
$\mathcal{N}_8$=q$\{Z,Z_3 \}$,96.
\end{frame}97.
\begin{frame}{Построениерешеток}
98.
$\mathcal{N}_9$=q$\{Z,Z_5 \}$,99.
$\mathcal{N}_{10}$=q$\{Z,Z_{15} \}$,100.
$\mathcal{N}_{11}$=q$\{Z,Z_{25} \}$,101.
$\mathcal{N}_{12}$=q$\{Z,Z_{75} \}$.102.
В результате получилирешетку,
изображенную на рис. 1.
Теорема доказана.
103.
\begin{block}{\ }104.
2. Квазимногообразиеq($Z_{7}$,$Z_{7^2}$,...,$Z_{10}$)
105.
\end{block}106.
\begin{block}{Теорема 5.}107.
Решетка$L_q(q(Z_{7},Z_{7^2},...,Z_{10}))$ - это
решетка,
изображенная на рис. 2.
108.
\end{block}109.
Доказательство.110.
\end{frame}111.
\begin{frame}{Построениерешеток}
112.
Сначала докажем, что Z$\in$ $q(Z_{7},Z_{7^2},...,Z_{10})$.
113.
$Z_{7}$=($a_1$), $Z_{7^2}=(a_2)$,...114.
$\bar a$ = ($a_1,a_2,a_3$,...)=(e,e,e,...).115.
$a^m_{1}$ = 1 $\rightarrow$ mделится на 7,
116.
$a^m_{2}$ = 1 $\rightarrow$ mделится на 49,
117.
...118.
Такого m несуществует. $\bar a^m$ $\neq$
1 для любого m $\rightarrow$
($\bar a$) = Z.
119.
Алгоритм построениярешетки
$L_q(q(Z_{7},Z_{7^2},...,Z_{10}))$.
120.
квазимногообразия,воспользовавшись
теоремой \ref{d20}. Для
этого заметим, что
$q(Z_{7},Z_{7^2},...,Z_{10})=q(Z_{7},Z_{7^2},...
,Z_{2},Z_{5})$.
121.
2) Вычисляем $\chi(q(Z_{7},Z_{7^2},...,Z_{10}))$.
122.
которыми могутпорождаться
подквазимногообразия
данного
квазимногообразия.
123.
\end{frame}124.
\begin{frame}{Построениерешеток}
125.
этом иногда добавляемк циклическим pгруппам ранее
найденные списки pгрупп.
126.
Пусть $\mathcal{M}$ =$q(Z_{7},Z_{7^2},...,Z_{10})$. Р
Р·
теоремы 5 следует, что
127.
1)Цикл(q($\mathcal{M}$)=$\{E,Z_2,Z_5,Z_{7},Z_{7^2},... \}$.
128.
2)$\chi (\mathcal{M})$=$\{1,2,5\}$129.
Отсюда из теоремы 1получаем, что $\mathcal{M}$
задается следующими
квазитождествами:
130.
($\forall$x)($\forall$y) (xy=yx),131.
($\forall$x)($x^4=1 \rightarrow x^2=1)$,132.
($\forall$x)($x^{25}=1 \rightarrow x^{5}=1)$,133.
($\forall$x)($x^{p^n+1}=1 \rightarrowx^p=1$), где p пробегает
множество простых
чисел, отличных от 2,5,7.
134.
\end{frame}135.
\begin{frame}{Построениерешеток}
136.
варианты дляподквазимногообразий
квазимногообразия
$\mathcal{M}$:
137.
3) Цикл($\mathcal{N}_1$)=E138.
Цикл($\mathcal{N}_2$) = $\{E,Z_2\}$139.
Цикл($\mathcal{N}_3$)=$\{E,Z_5\}$140.
Цикл($\mathcal{K}_n$)=$\{E,Z_{7},Z_{7^2},...,Z_{7^n} \}$ (n=1,2,...),
141.
Цикл($\mathcal{M}_n$)=$\{E,Z_2,Z_{7},Z_{7^2},...,Z_{7^n} \}$ (n=1,2,...),
142.
Цикл($\mathcal{R}_n$)=$\{E,Z_5,Z_{7},Z_{7^2},...,Z_{7^n} \}$ (n=1,2,...),
143.
Цикл($\mathcal{N}_7$)=$\{E,Z_2,Z_5\}$,
144.
Цикл($\mathcal{L}_n$)=$\{E,Z_2,Z_5,Z_{7},Z_{7^2},...,Z_{7^n} \}$ (n=1,2,...).
145.
\end{frame}146.
\begin{frame}{Построениерешеток}
147.
Возможны следующиеквазимногообразия:
148.
$\mathcal{N}_1$=qE,149.
$\mathcal{N}_2$=q$Z_2$,150.
$\mathcal{N}_3$=q$Z_5$,151.
$\mathcal{K}_n$=q$\{Z_{7^n} \}$,152.
$\mathcal{M}_n$=q$\{Z_2,Z_{7^n} \}$,153.
$\mathcal{R}_6$=q$\{Z_5,Z_{7^n} \}$,154.
$\mathcal{N}_7$=q$\{Z_2,Z_5 \}$,155.
$\mathcal{L}_n$=q$\{Z_2,Z_5,Z_{7^n} \}$,156.
$\mathcal{N}_9$=qZ,157.
$\mathcal{N}_{10}$=q$\{Z,Z_2 \}$,158.
$\mathcal{N}_{11}$=q$\{Z,Z_5 \}$,159.
qZ $\cup$ $\mathcal{K}_{n}$=q$\{Z,Z_{7^n}\}$,
160.
qZ $\cup$$\mathcal{M}_{n}$=q$\{Z,Z_2,Z_{7^n} \}$,
161.
qZ $\cup$$\mathcal{R}_{n}$=q$\{Z,Z_5,Z_{7^n} \}$,
162.
$\mathcal{N}_{15}$=q$\{Z,Z_2,Z_5 \}$,163.
qZ $\cup$$\mathcal{L}_{n}$=q$\{Z,Z_2,Z_5,Z_{7^n} \}$.
164.
\end{frame}165.
\begin{frame}{Построениерешеток}
166.
подквазимногообразия,содержащие
бесконечное
множество
циклических 7-групп:
167.
$q(Z_{7},Z_{7^2},Z_{7^3},...)$,$q(Z_{7},Z_{7^2},...,Z_{2})$, $q(Z_{7},Z_{7^2},...,Z_{5})$,
$q(Z_{7},Z_{7^2},...,Z_{2},Z_{5})$ =
$\mathcal{M}$.
168.
решетка $L_q$($\mathcal{M}$) это решетка,изображенная на рис. 2.
Теорема доказана.
169.
\end{frame}170.
\begin{frame}{Рисункирешеток}
































































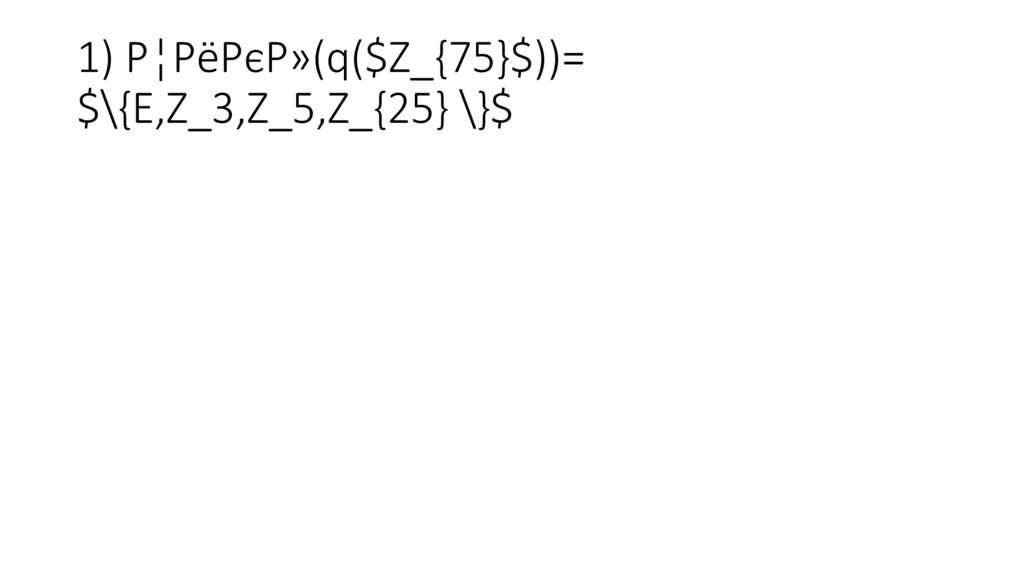


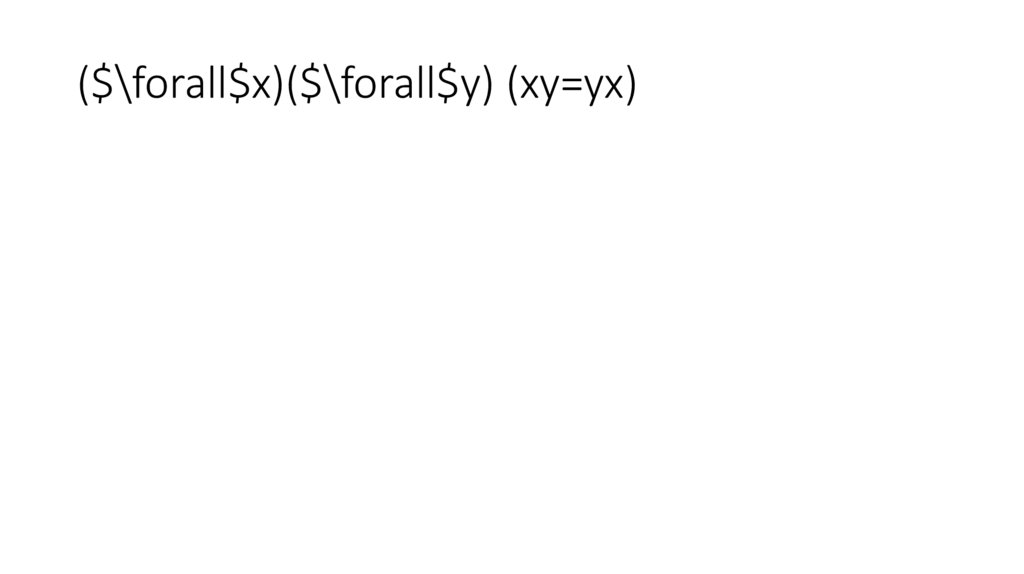
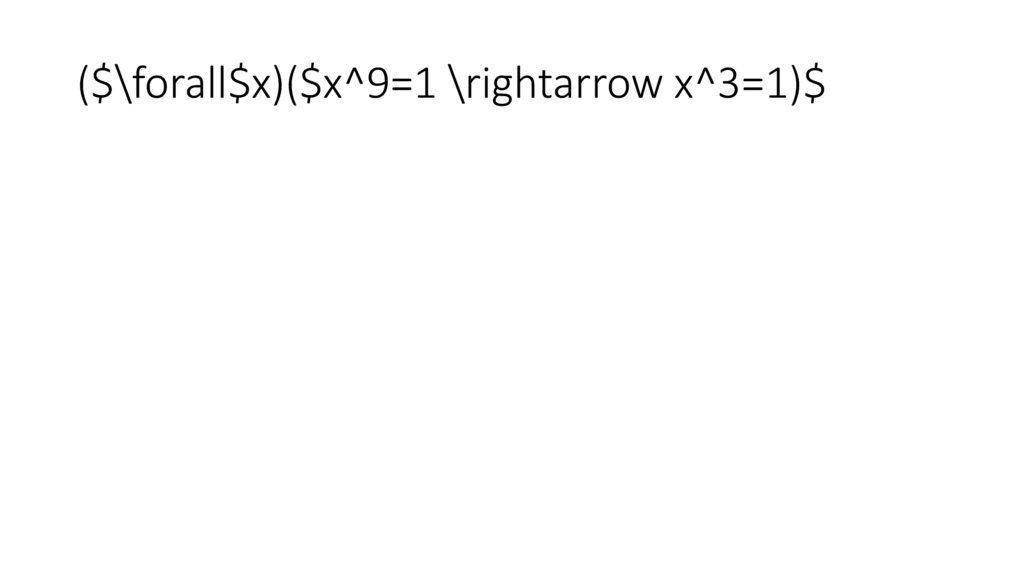

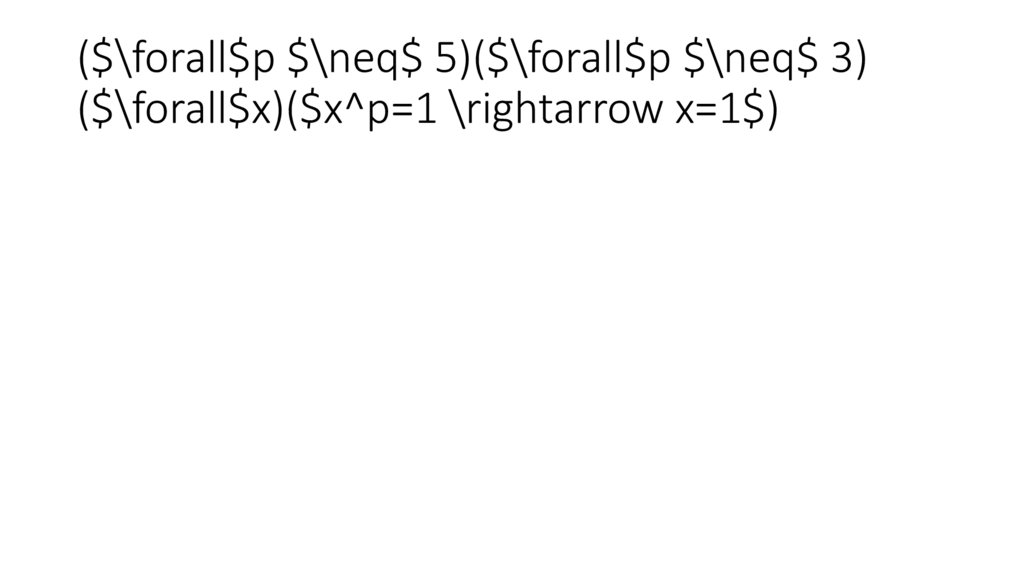


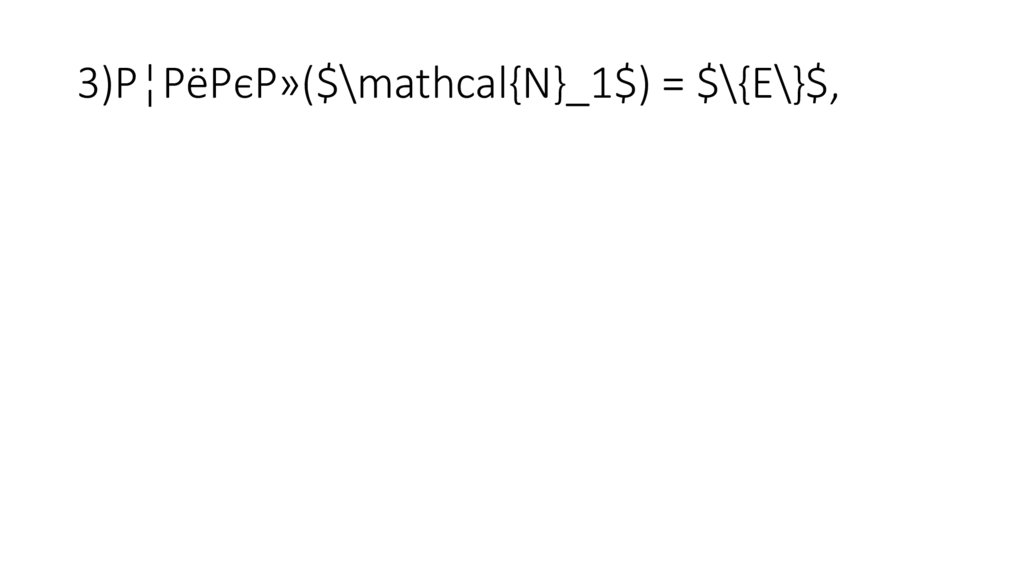
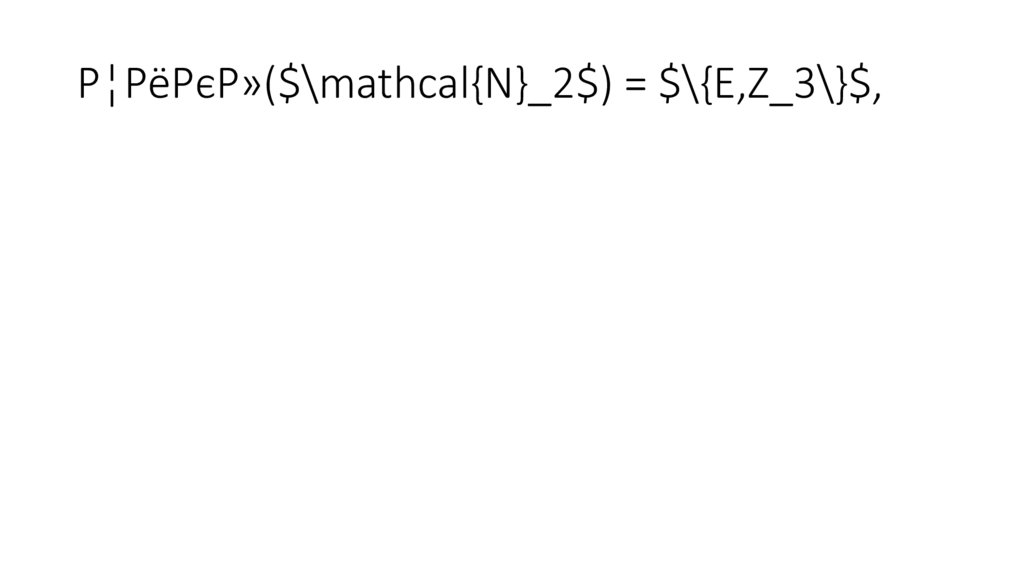
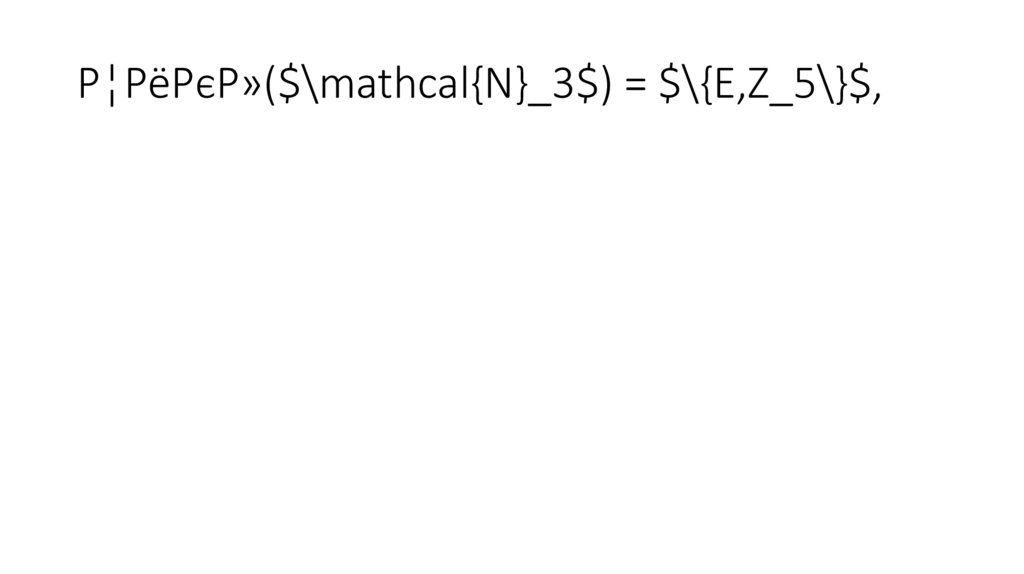

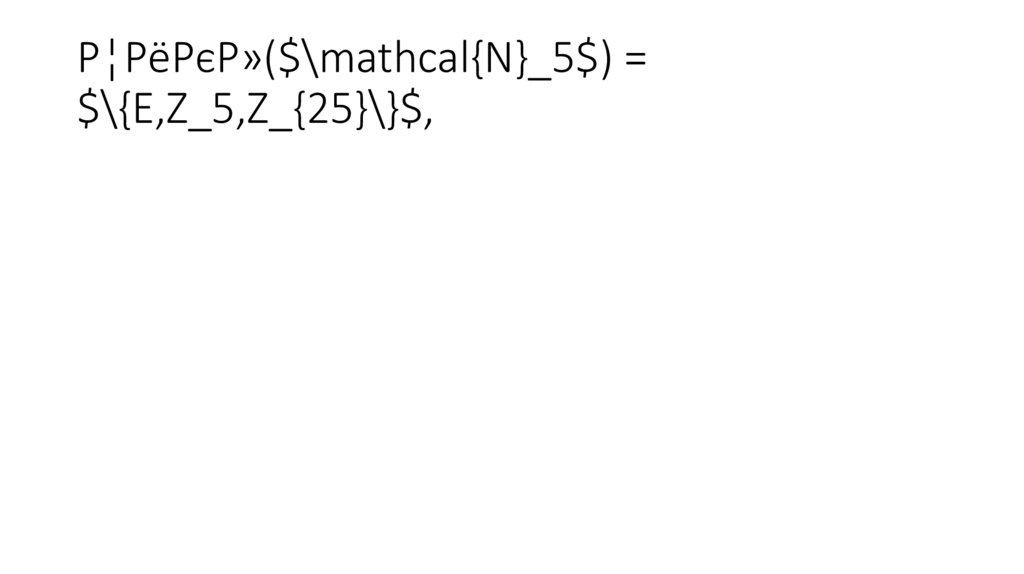










































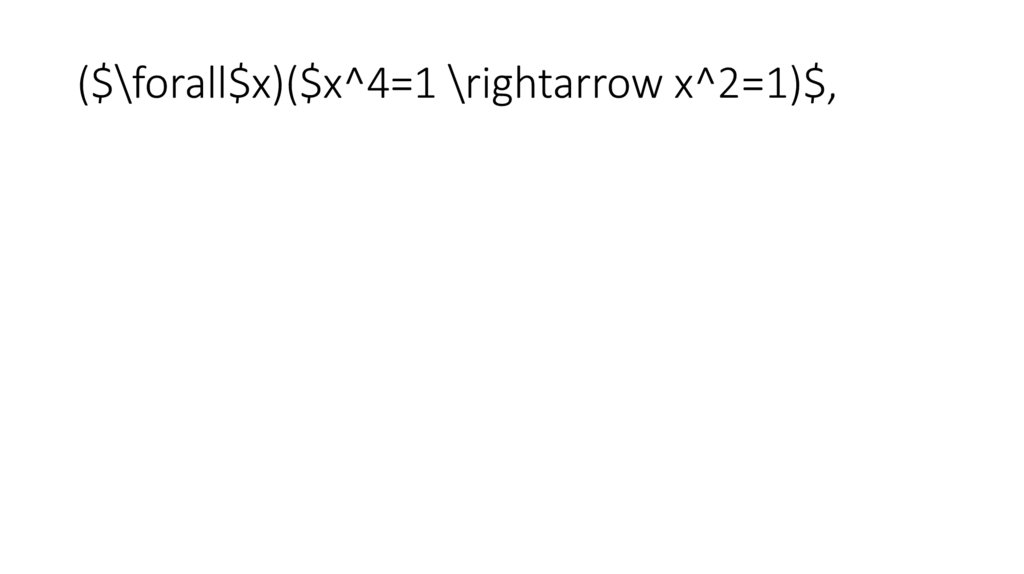
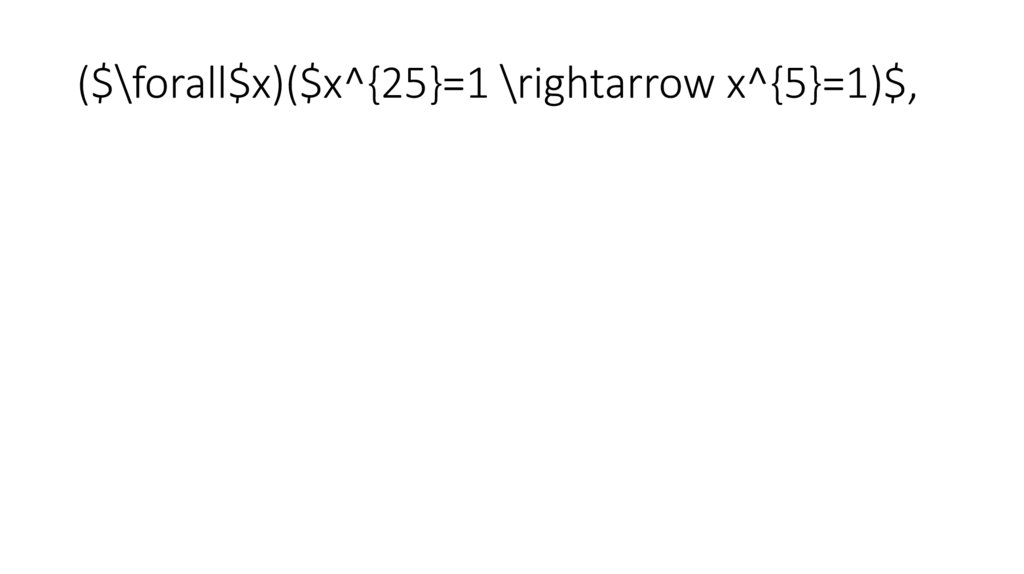




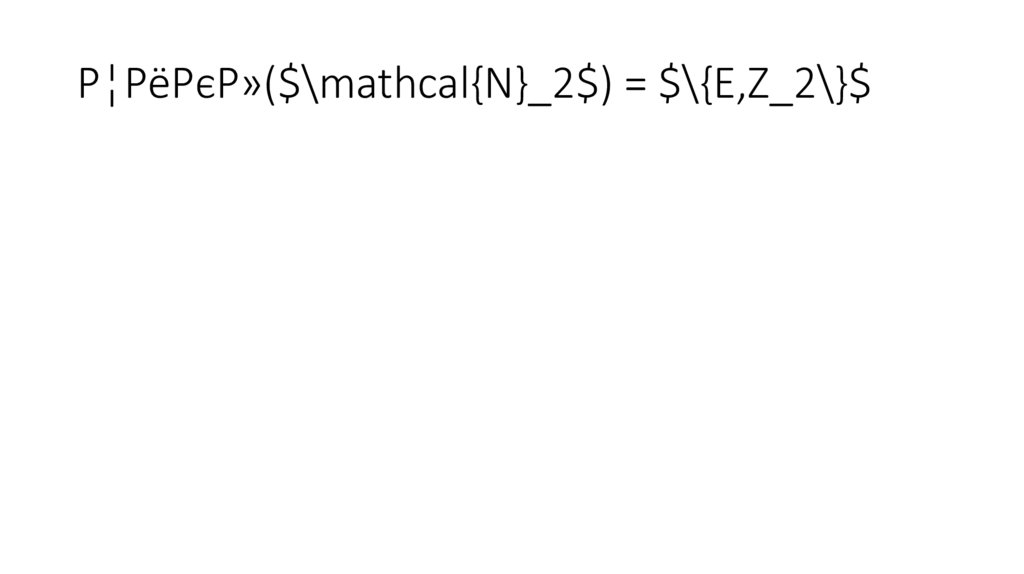


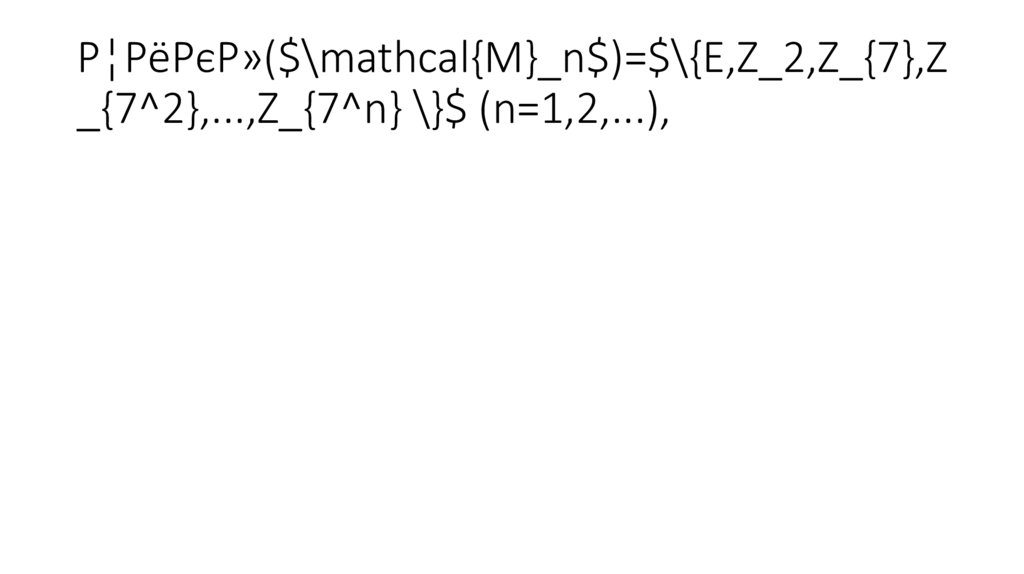





























 programming
programming








