Similar presentations:
Золотое сечение
1.
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ«ВОЖЕГОДСКАЯ СРЕДНЯЯ ШКОЛА»
Научно исследовательская работа по теме : «Золотое сечение – красота и
гармония в математических расчетах.»
ВЫПОЛНИЛ: ШОХОВ ТИМОФЕЙ,
УЧЕНИК 9 «Б» КЛАССА
РУКОВОДИТЕЛЬ ПРОЕКТА:
ШАГАЛОВА АНТОНИНА ВАСИЛЬЕВНА,
УЧИТЕЛЬ МАТЕМАТИКИ
2.
ЦЕЛЬ РАБОТЫ• Выявить, что же такое золотое сечение, исследовать принцип “золотого сечения – красоты и
гармонии” в окружающем мире.
ОСНОВНЫЕ ЗАДАЧИ
• Изучить красоту окружающих предметов с математической точки зрения.
• Найти в математической литературе подтверждение гипотезы исследования.
• Провести эксперименты по поиску идеальных пропорций в красивых предметах.
ЭТАПЫ ВЫПОЛНЕНИЯ ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ
• Подбор и изучение, необходимой для исследования литературы.
• Сбор и систематизация материала.
• Экспериментальная проверка фактов, подтверждающих гипотезу проекта.
• Оформление результатов исследовательской деятельности.
3.
Понятие «золотого сечения»золотое сечение – это деление отрезка, при котором длина всего отрезка так относится к длине его
большей части, как длина большей части к меньшей.
с:в = в:а
отношение обозначают буквой ( фи );
= 1,618 = 8/5
Золотое сечение математики часто называли божественной пропорцией
Скульпторы, архитекторы, художники использовали и
используют золотое сечение в своих произведениях.
К примеру, в храме П арфенон в Афинах отношение высоты
здания к его длине равно .
4.
Есть предположение, что Пифагор понятие золотого сечения позаимствовал у египтян и вавилонян. И, действительнопропорции пирамиды Хеопса, барельефы предметов быта и украшений из гробницы Тутанхамона свидетельствуют,
что египетские мастера пользовались соотношением золотого сечения при их создании.
Очень совершенна форма стрекозы, которая создана по
законам золотой пропорции : отношение длин хвоста и
корпуса равно отношению общей длины к длине хвоста
Рассматривая расположение листьев на стебле растений
можно заметить, что между каждыми двумя парами листьев
(А и С) третья расположена в месте золотого сечения (В).
Холст, на котором написана «Тайная
вечеря» Сальвадора Дали, имеет форму
золотого прямоугольника, стороны которого
находятся в золотом отношении.
5.
Числа Фибоначчи - удивительные числа, которые были открыты итальянским математиком средневековьяЛеонардо П изанским, более известным под именем Фибоначчи. Удивительная суть последовательности чисел
Фибоначчи состоит в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584
Более того, после 13-ого числа в последовательности этот результат деления становится постоянным до
бесконечности ряда… Именно это постоянное число деления в средние века было названо
Божественной пропорцией или золотое сечение.
В математике это число обозначается греческой
буквой фи (Ф).
Золотая пропорция = 1 : 1,618
6.
ФоторамкаИсследования.
Мне захотелось проверить, что «Золотая пропорция» действительно является
универсальным информационным кодом. И я провел следующие эксперименты.
Цель исследования : выявить, действительно ли форма золотого прямоугольника создает впечатление
красоты и гармонии
Оборудование : лист ватмана с рисунками фоторамок различных размеров.
Вопрос: какая фоторамка лучше подходит для предложенной фотографии?
7.
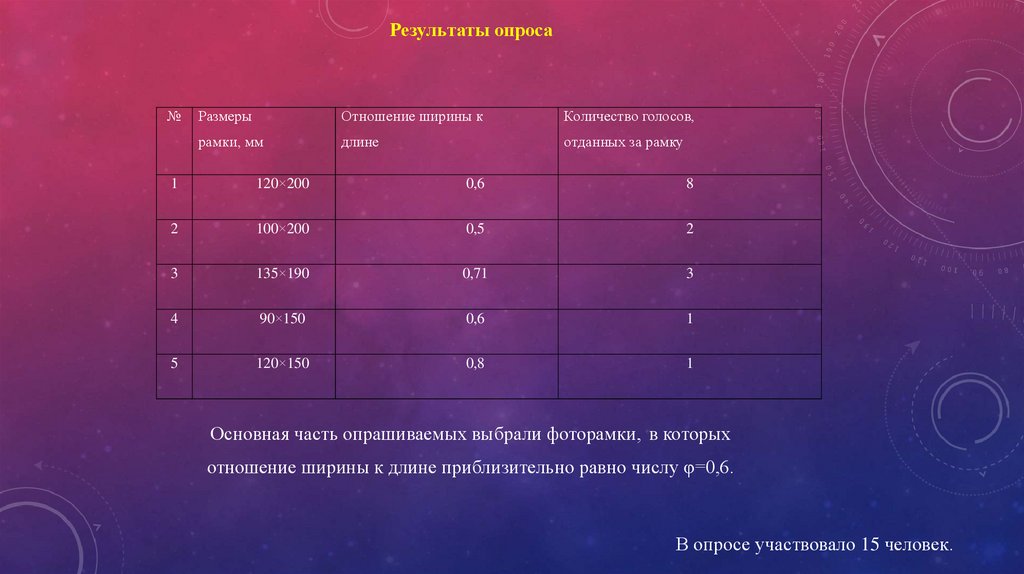
Результаты опроса№
Размеры
Отношение ширины к
Количество голосов,
рамки, мм
длине
отданных за рамку
1
120×200
0,6
8
2
100×200
0,5
2
3
135×190
0,71
3
4
90×150
0,6
1
5
120×150
0,8
1
Основная часть опрашиваемых выбрали фоторамки, в которых
отношение ширины к длине приблизительно равно числу φ=0,6.
В опросе участвовало 15 человек.
8.
Эксперимент «Узел»Цель: исследовать форму узла
Оборудование: полоска бумаги постоянной ширины, чертежные инструменты, мужской галстук.
Ход эксперимента:
Бумажную ленту постоянной ширины завяжем простым узлом и расправим так, чтобы узел был плоским.
Получается узел, имеющий форму пятиугольника. Измерения сторон и углов пятиугольника доказывают, что
ABCDE - правильный пятиугольник.
D
Отношение стороны правильного
пятиугольника к диагонали равно числу
С
E
Вывод: узел имеет форму правильного пятиугольника, т.е.
пентаграммы. Пентаграмма – это геометрический символ
гармонии, здоровья и мистических сил.
А
В
9.
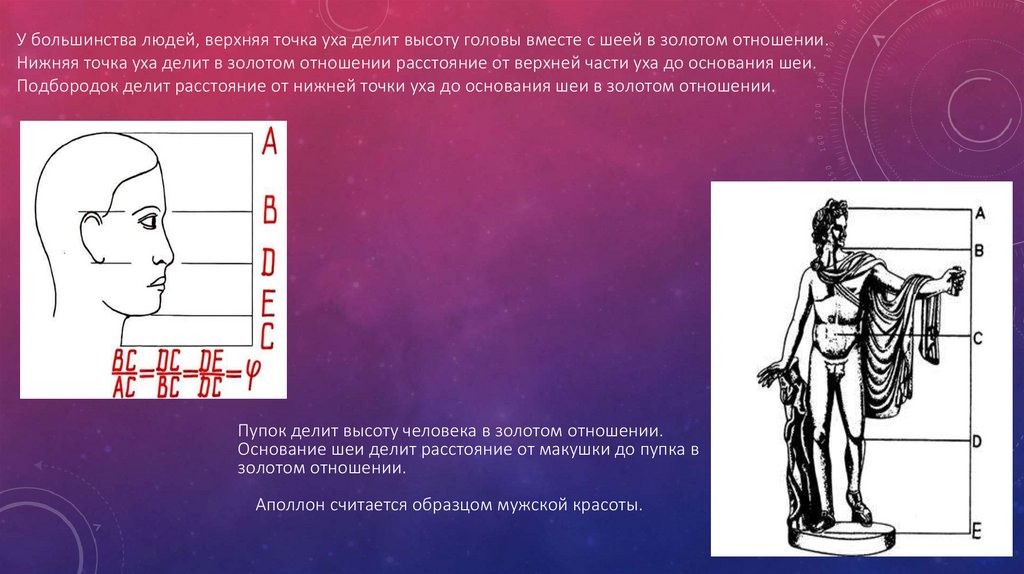
У большинства людей, верхняя точка уха делит высоту головы вместе с шеей в золотом отношении.Нижняя точка уха делит в золотом отношении расстояние от верхней части уха до основания шеи.
Подбородок делит расстояние от нижней точки уха до основания шеи в золотом отношении.
Пупок делит высоту человека в золотом отношении.
Основание шеи делит расстояние от макушки до пупка в
золотом отношении.
Аполлон считается образцом мужской красоты.
10.
Вывод:Творения человека тоже подчиняются удивительному закону золотого сечения. Всё красивое и
гармоничное, что сумеет сделать человек, содержит в себе золотые пропорции.
Я убедился, что все-таки существует связь между математикой и литературой, между математикой и
архитектурой, между математикой и живописью. И это не случайно, ведь каждому искусству присуще
стремление к стройности, соразмерности, гармонии. Природа совершенна, и у нее есть свои законы,
выраженные с помощью математики и проявляющиеся в различных видах искусства.
Меня поразил тот факт, что даже планеты солнечной системы обращаются вокруг солнца по орбитам с
«золотым сечением», а Земля имеет самую совершенную орбиту из всех планет. Это доказали математики!









 mathematics
mathematics








