Проверка статистических выборок на принадлежность к генеральной совокупности. Практическое занятие

1. Практическое занятие

Проверка статистических
выборок
на принадлежность к
генеральной совокупности
Практическое занятие

2. Проверка статистических выборок на принадлежность к генеральной совокупности

СЛАЙД 1
Проверка статистических выборок
на принадлежность к генеральной совокупности
Оценка возможности объединения нескольких групп статистических наблюдений
в единую статистическую выборку производится с использованием
2
χ̂
непараметрического критерия
(«хи-квадрат»)
Сущность этой оценки – проверка гипотезы о равенстве функций распределения
наработок до отказа, при принятом уровне доверительности = 1- .
χˆ 2 χ 12 α r
где χ̂
2
– непараметрический критерий «хи-квадрат», вычисляемый
по результатам наблюдений из выражения:
i
j
ˆ 2
i 1 j 1
nij2
pi p j N в
Nв
где i , j – количество классов (интервалов) и рядов выборки соответственно;
nij – количество наблюдений, попавших в i-ый интервал j-го ряда
Nв – число наблюдений в статистической выборке;
pi – вероятность попадания наблюдений в i-ый интервал;
pj – вероятность попадания наблюдения в j-ый ряд.

3. Продолжение

СЛАЙД 2
Продолжение
Вероятность попадания наблюдений в j - ый ряд pj и i - ый интервал pi оценивается
по формулам:
Nj
N
pj
pi i
Nв
Nв
где Nj – число наблюдений в j-ом ряду;
Ni – число наблюдений в i-ом интервале.
χ12 α r – критическое значение критерия 2 –распределения, отыскиваемое
из статистических таблиц (Приложение 2) в зависимости
от заданного уровня значимости и степени свободы r,
определяемой из формулы:
r j 1 i 1
Для вычисления функции ̂ статистическая выборка подвергается группированию.
2
Все значения полученных наблюдений подразделяют на 3…5 групп.
Каждая группа получает название ряда. Количественное наполнение рядов выборки
регулируют так, чтобы они содержали примерно равное число наблюдений.
Далее ряды разбивают на классы или интервалы. При этом соблюдают правило, чтобы
каждый интервал включал не менее 4…5 наблюдений. Ориентировочно число интервалов
можно определить по правилу Штургеса: ki = 1+3.32lg Nв

4.

СЛАЙД 3
Пример. При испытании уплотнительных устройств, проведенных
в разное время и на разных объектах, получены три статистические выборки,
характеризующие наработку исследуемых объектов до отказа, измеренную в часах:
Выборка №1: 9;10;11;7;8;14;12;7;10;13;9;10;12;8;9, (Nв1=15).
Выборка№2: 10;11;7;10;8:9;12;10;7;13;9;8;14;10;9;12;9;8;9; 11;8;10;9;10,(Nв2=24)
Выборка №3: 10;7;9;12;8;10;10;7;11;9;8;12;10;8;9;11; 9;12;10;8;11;9, (Nв3=22).
Оценить возможность объединения трех статистических выборок
в единую генеральную совокупность.
Решение. Выполняется группирование выборок:
- подсчитывается общее число наблюдений
N в N в1 N в 2 N в 3 15 24 22 61
- принимается число рядов j = 3;
- определяется число наблюдений в ряду N j 61 : 3 20 (ориентировочно);
- рассчитывается число интервалов; i = 1+3.32 lgNj=1+3,32 lg20 ≈ 5.
Для рассматриваемого случая достаточно i = 3 (7-8 час; 9-10 час; 11-14 час).

5.

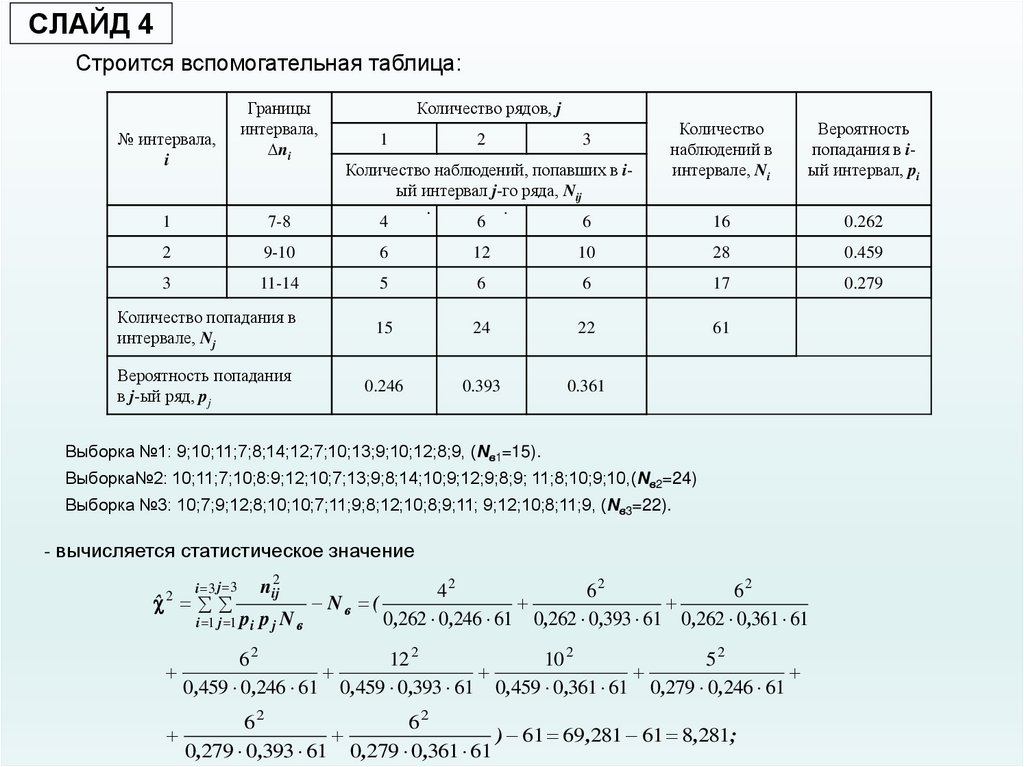
СЛАЙД 4
Строится вспомогательная таблица:
№ интервала,
i
Границы
интервала,
ni
Количество рядов, j
1
7-8
4
6
2
9-10
6
3
11-14
Количество
наблюдений в
интервале, Ni
Вероятность
попадания в iый интервал, pi
6
16
0.262
12
10
28
0.459
5
6
6
17
0.279
Количество попадания в
интервале, Nj
15
24
22
61
Вероятность попадания
в j-ый ряд, pj
0.246
0.393
0.361
1
2
3
Количество наблюдений, попавших в iый интервал j-го ряда, Nij
Выборка №1: 9;10;11;7;8;14;12;7;10;13;9;10;12;8;9, (Nв1=15).
Выборка№2: 10;11;7;10;8:9;12;10;7;13;9;8;14;10;9;12;9;8;9; 11;8;10;9;10,(Nв2=24)
Выборка №3: 10;7;9;12;8;10;10;7;11;9;8;12;10;8;9;11; 9;12;10;8;11;9, (Nв3=22).
- вычисляется статистическое значение
i 3 j 3
nij2
42
62
62
Nв (
0 ,262 0 ,246 61 0 ,262 0 ,393 61 0 ,262 0 ,361 61
i 1 j 1 p i p j N в
ˆ
2
62
12 2
10 2
52
0 ,459 0 ,246 61 0 ,459 0 ,393 61 0 ,459 0 ,361 61 0 ,279 0 ,246 61
62
62
) 61 69 ,281 61 8 ,281;
0 ,279 0 ,393 61 0 ,279 0 ,361 61

6.

СЛАЙД 5
- определяется число степеней свободы:
r = (j – 1) (i – 1) = (3 – 1) (3 – 1) = 4;
По таблице Приложения 2 распределения “хи-квадрат” отыскивается значение
12 0 ,05 r 4 при заданном уровне значимости α = 0,05:
02 ,95 4 9 ,488
Проверяется неравенство
χˆ 2 χ 12 α r
ˆ 2 02 ,95 4 8 ,281 9 ,488
Неравенство выполняется. Это значит, что представленные статистические
выборки принадлежат к единой генеральной совокупности и могут быть
приняты к статистической обработке в целом.