Представление о правильных многогранниках

1. ПРЕДСТАЛЕНИЕ О ПРАВИЛЬНЫХ МНОГОГРАННИКАХ

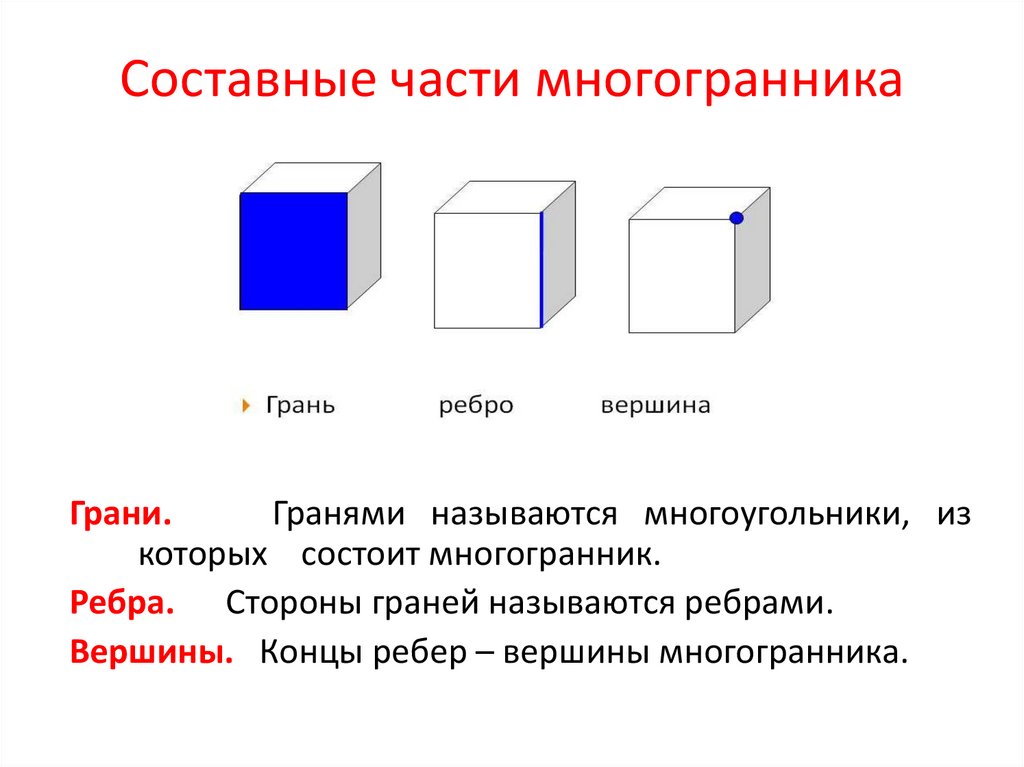
2. Составные части многогранника

Грани.
Гранями называются многоугольники, из
которых состоит многогранник.
Ребра. Стороны граней называются ребрами.
Вершины. Концы ребер – вершины многогранника.

3. Выпуклые и невыпуклые многогранники

Многогранники бывают: выпуклыми и невыпуклыми.
Выпуклый многогранник расположен по одну сторону
от плоскости каждой своей грани.
Невыпуклый многогранник расположен по разные
стороны от одной из плоскости.
Выпуклый многогранник
Невыпуклый многогранник

4. ТЕТРАЭДР

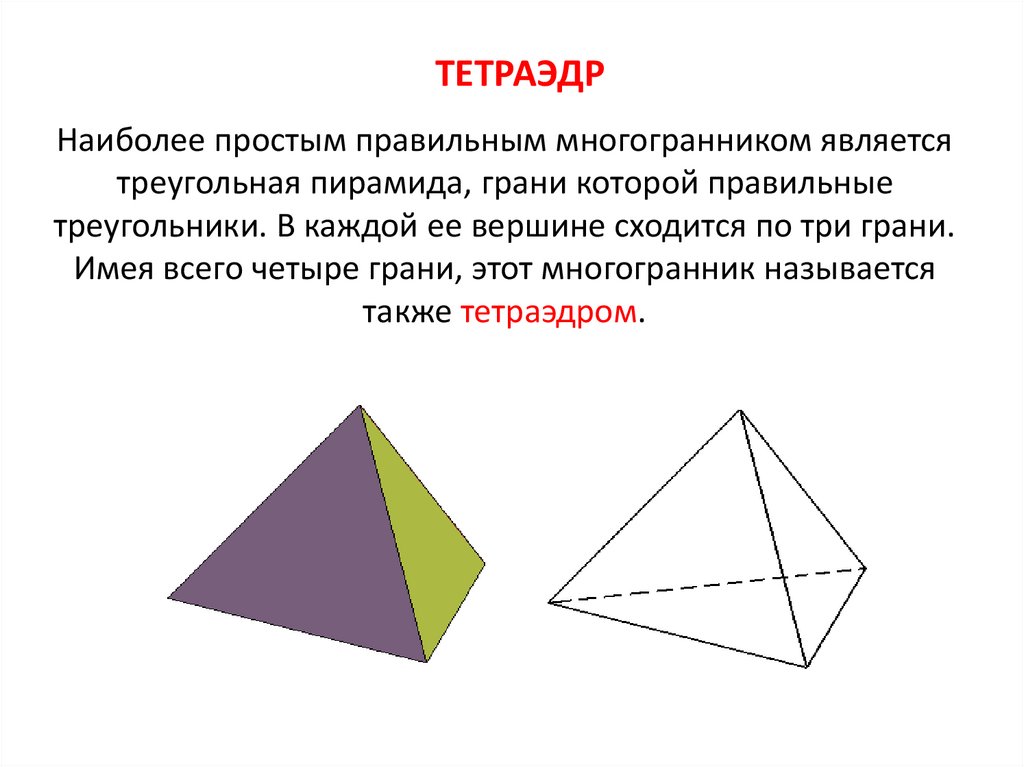
ТЕТРАЭДР
Наиболее простым правильным многогранником является
треугольная пирамида, грани которой правильные
треугольники. В каждой ее вершине сходится по три грани.
Имея всего четыре грани, этот многогранник называется
также тетраэдром.

5. Упражнение 1

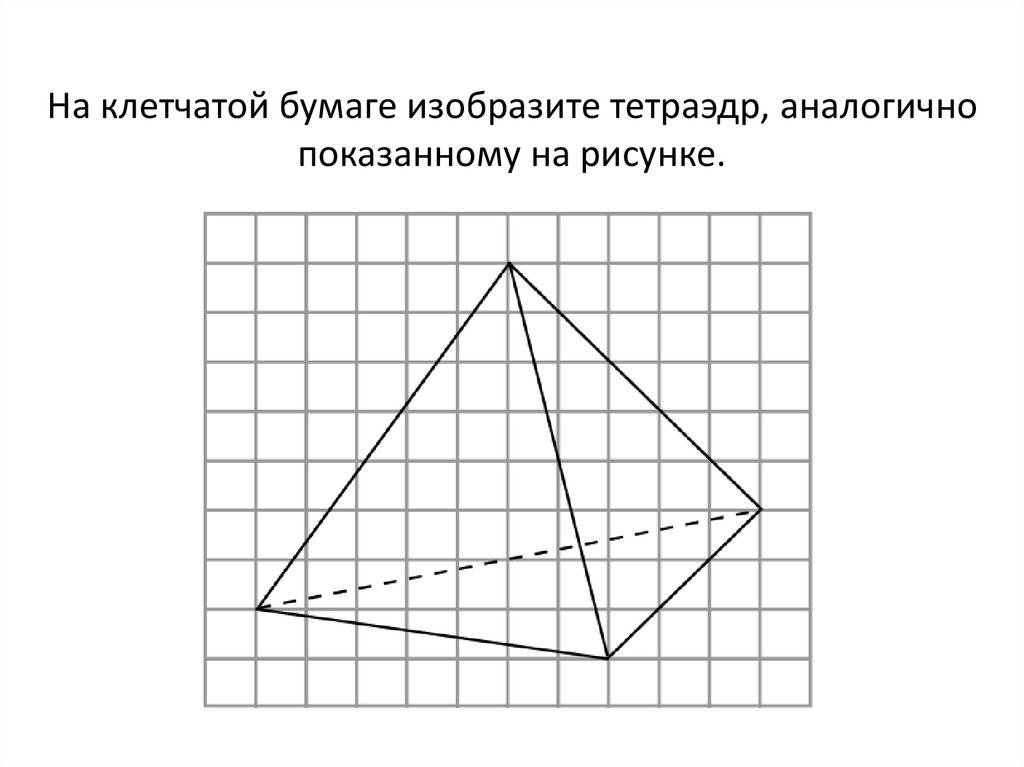
На клетчатой бумаге изобразите тетраэдр, аналогично
показанному на рисунке.

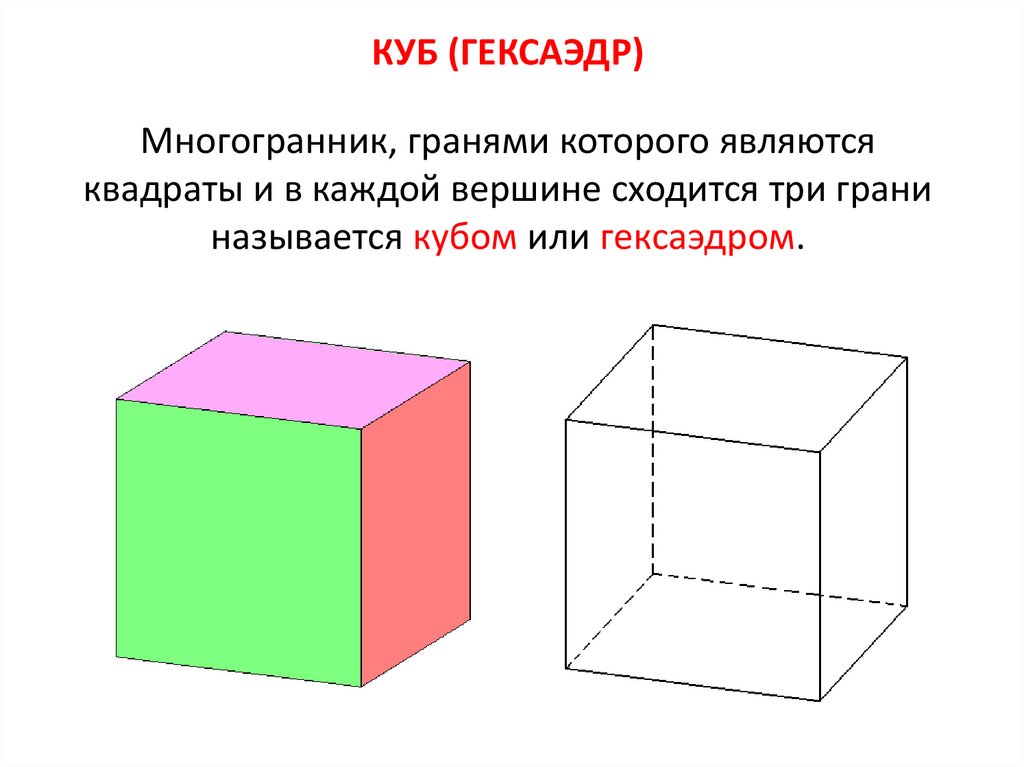
6. КУБ (ГЕКСАЭДР)

Многогранник, гранями которого являются
квадраты и в каждой вершине сходится три грани
называется кубом или гексаэдром.

7.

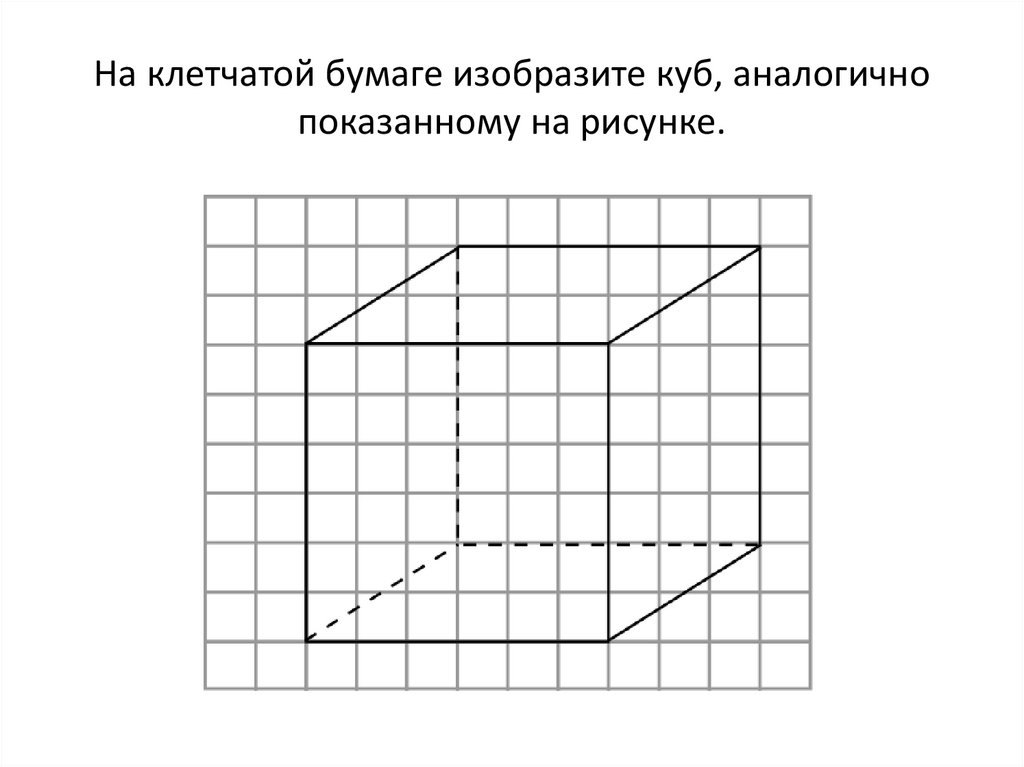
На клетчатой бумаге изобразите куб, аналогично
показанному на рисунке.

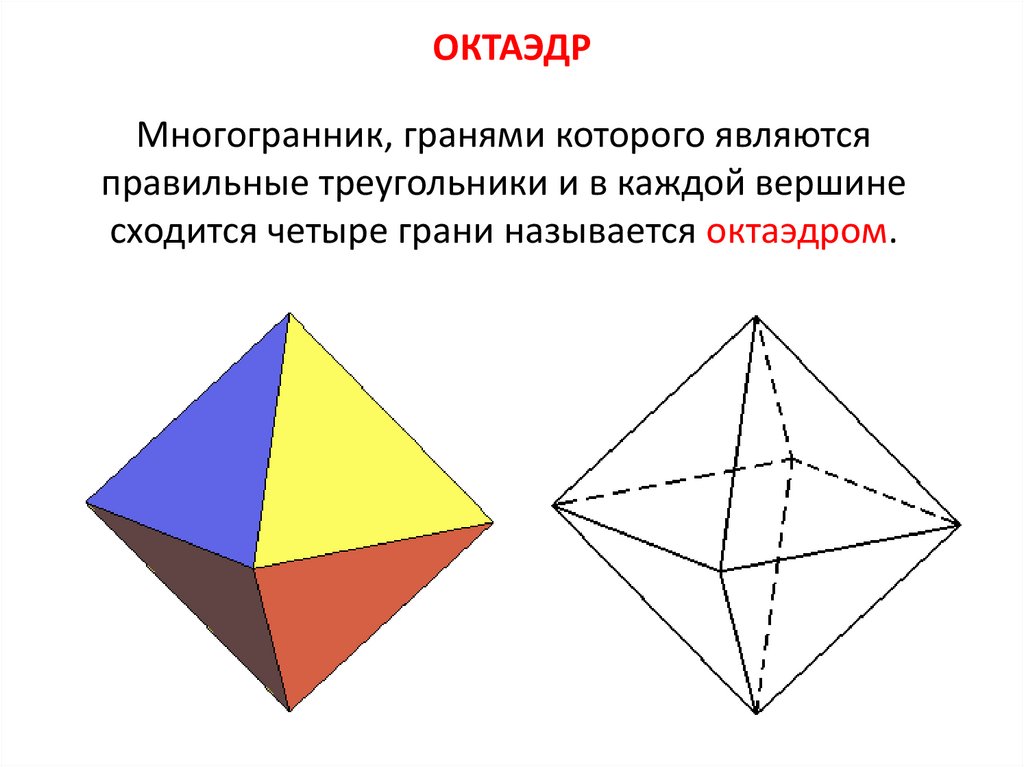
8. ОКТАЭДР

Многогранник, гранями которого являются
правильные треугольники и в каждой вершине
сходится четыре грани называется октаэдром.

9.

На клетчатой бумаге изобразите октаэдр, аналогично
показанному на рисунке.

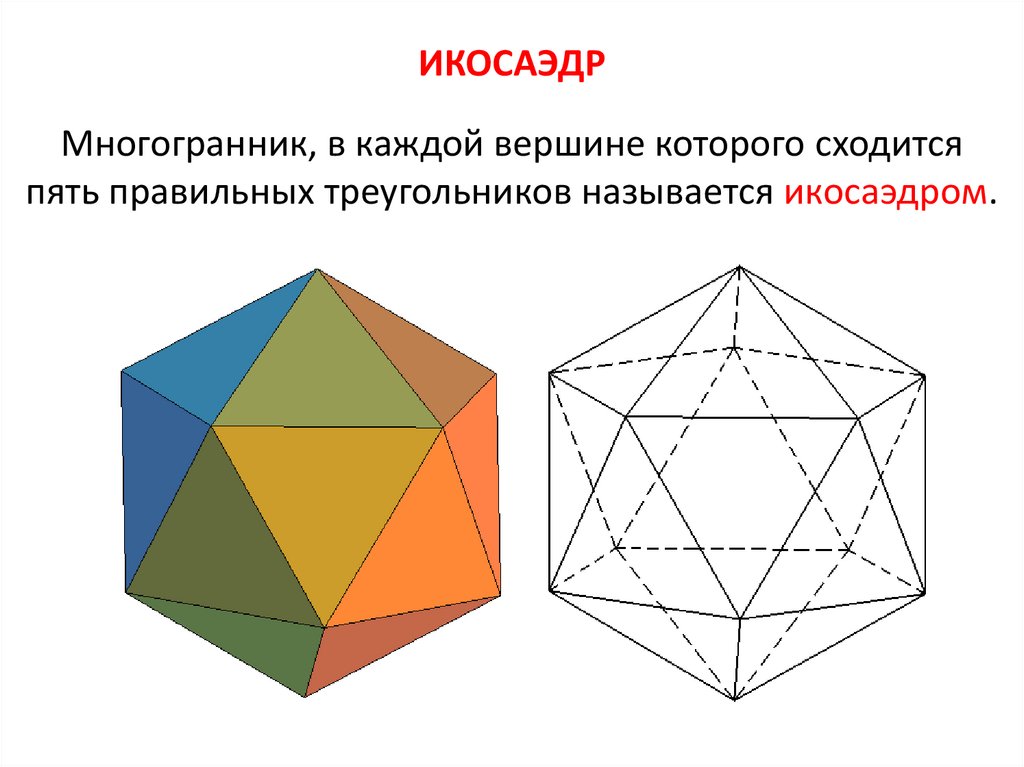
10. ИКОСАЭДР

Многогранник, в каждой вершине которого сходится
пять правильных треугольников называется икосаэдром.

11.

На клетчатой бумаге изобразите икосаэдр, аналогично
показанному на рисунке.

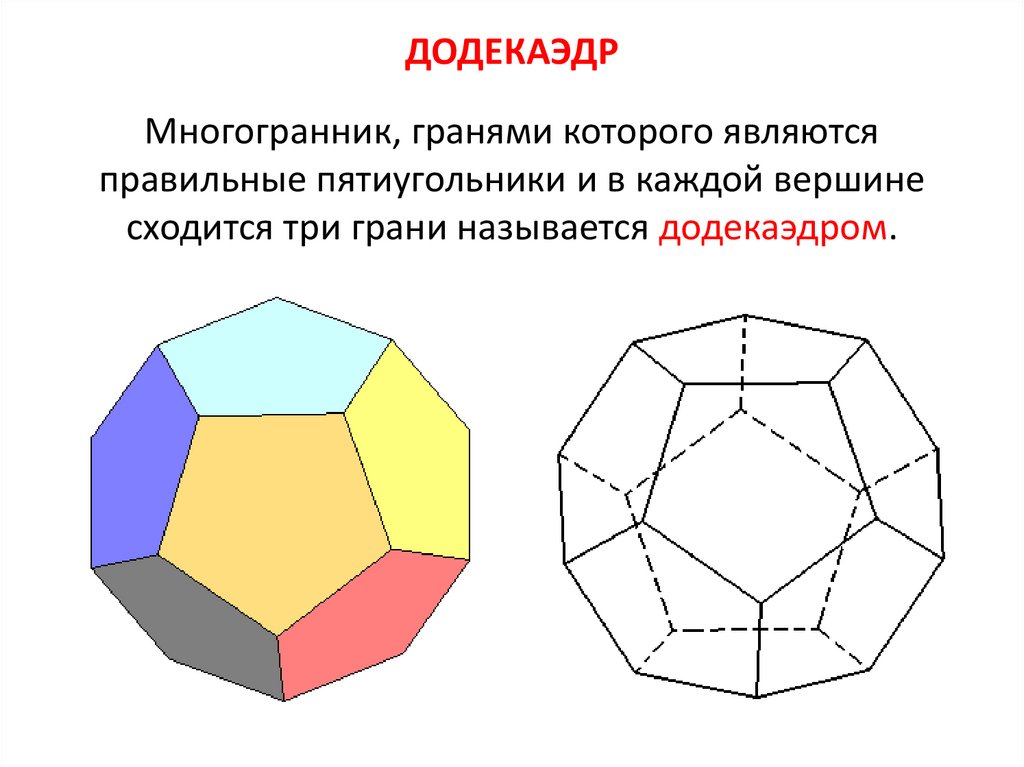
12. ДОДЕКАЭДР

Многогранник, гранями которого являются
правильные пятиугольники и в каждой вершине
сходится три грани называется додекаэдром.

13.

На клетчатой бумаге изобразите додекаэдр, аналогично
показанному на рисунке.

14. Великим математиком, физиком и астрономом Леонардом Эйлером (1707 - 1783) была доказана удивительная теорема.

Теорема Эйлера. Для любого выпуклого
многогранника
В + Г Р = 2,
где В – число вершин,
Г – число граней,
Р – число ребер этого многогранника.

15.

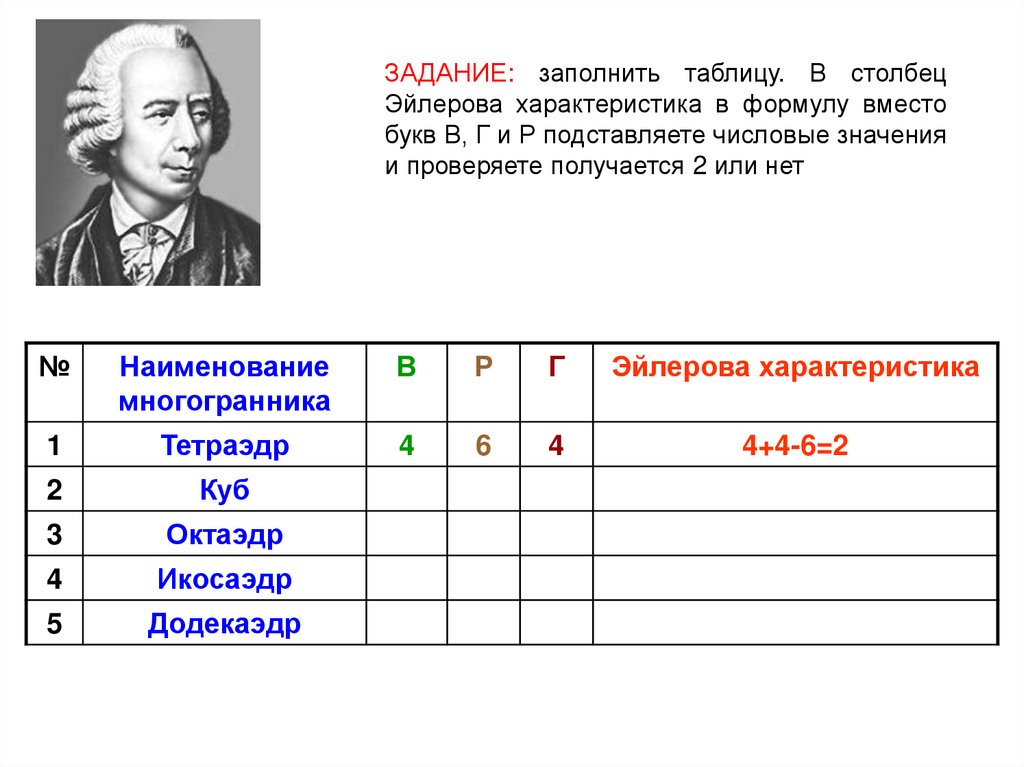
ЗАДАНИЕ: заполнить таблицу. В столбец
Эйлерова характеристика в формулу вместо
букв В, Г и Р подставляете числовые значения
и проверяете получается 2 или нет
№
Наименование
многогранника
В
Р
Г
Эйлерова характеристика
1
Тетраэдр
4
6
4
4+4-6=2
2
Куб
3
Октаэдр
4
Икосаэдр
5
Додекаэдр

16. СПАСИБО ЗА ВНИМАНИЕ!