Наиболее эффективные приемы, используемые при моделировании расчетных схем (лекция 7)

1.

ЛЕКЦИЯ 7
НАИБОЛЕЕ ЭФФЕКТИВНЫЕ ПРИЕМЫ,
ИСПОЛЬЗУЕМЫЕ ПРИ
МОДЕЛИРОВАНИИ РАСЧЕТНЫХ СХЕМ

2.

Стратификация.
Какой бы подробной ни была компьютерная
модель, она всегда будет оставаться моделью,
т.е. будет только моделировать различные
свойства конструкции, причем, как правило, с
различной степенью точности.

3.

Исследование
конструкции
на
основе
системы
компьютерных
моделей,
каждая
из
которых
рассматривает систему в целом и моделирует с
различным приближением то или иное свойство, по
своей логике близко к приемам стратификации,
применяемым в общей теории систем.
Так, при расчете конструкций высотных зданий часто
принимаются следующие стратификационные модели.

4.

Страт 1. Исследования деформативности здания на
горизонтальные воздействия.
Здесь
применяется
компьютерная
модель,
характерная тем, что плита перекрытия моделирует
только передачу горизонтальных усилий на
вертикальные
несущие
элементы
(колонны,
диафрагмы), поэтому их разбивка на конечные
элементы может быть достаточно крупной.

5.

Кроме того, диафрагмы ввиду того, что их высота
значительно превышает поперечные размеры, могут
быть заменены стержневыми элементами расчет на
горизонтальные воздействия (ветер с учетом пульсации,
сейсмика) всегда связан с проведением динамического
расчета, с одной стороны, требующего больших
ресурсов, с другой стороны, характеризующегося
большими приближениями в задании исходных данных.
Поэтому использование упрощенной расчетной схемы
вполне оправдано.

6.

Страт 2. Исследования прочности и
деформативности плиты перекрытия.
Расчет плиты перекрытия без учета ее работы в
системе каркаса может привести к серьезным
упущениям поэтому ее следует рассчитывать в
общей схеме, однако влияние деформативности
всего каркаса может быть учтено приближенно.

7.

В этом случае плита перекрытия должна иметь
подробную
густую
конечноэлементную
сетку,
подробное моделирование узлов опирания этой
плиты на колонны и диафрагмы, подробные схемы
приложения вертикальной нагрузки. Учет влияния
каркаса здесь может быть достаточно упрощен,
например, по аналогии со стратом 1.

8.

Страт 3. Исследования напряженнодеформированного состояния диафрагмы.
Здесь подобно страту 2 исследуемая диафрагма
имеет
более
подробную
конечно-элементную
модель. Элементы остального каркаса моделируются
по упрощенной схеме. Исследование работы плиты,
подпертой ребрами, также может быть проведено на
основе стратов:

9.

Страт 1. Плита совместно с балочным ростверком.
Страт 2. Плита совместно со стержневой системой,
подвешенной к узлам плиты на абсолютно жестких
вставках.
Страт 3. Плита, имеющая утолщенные конечные
элементы в местах, соответствующих расположению
балок.

10.

Каждый из этих стратов имеет свои преимущества и
недостатки. Так, страт 1 удобен для дальнейшего
конструирования, но требует предварительного
ответа на вопрос о том, какую часть плиты следует
включить в полку тавровой балки. Страт 2, повидимому,
более
точно
моделирует
работу
конструкции, но трудоемок в синтезе и анализе.

11.

Страт 3 удобен при задании исходных данных, но
требует более густой сетки, наличия конечных
элементов толстых плит и др. Во всяком случае,
если инженер обладает временем, терпением и
желанием проникнуть в суть задачи, то исследование
всех трех стратов даст ему обильную и добротную
пищу для размышлений.

12.

Фрагментация.
Под фрагментацией будем понимать выделение из
конструкции
некоторой
ее
части
в
целях
последующего включения в расчетную схему только
этой выделенной части конструкции, называемой
фрагментом.
Будем анализировать
процедуру:
следующую
двухэтапную

13.

Пренебрегая
локальными
особенностями
конструктивного решения, строится затрубленная
расчетная схема полной конструкции в первом
приближении, которая дает возможность оценить
напряженно-деформированное состояние объекта в
целом, и выполняется ее расчет.

14.

• Выделяется фрагмент конструкции, содержащий
интересующую нас особенность. К этому фрагменту
прикладываются
силы,
непосредственно
приложенные к выделенной части конструкции.
Полная
граница
фрагмента
образуется
объединением двух частей.

15.

Г = Г1 U Г2, где Г1 — часть границы фрагмента
(которая может быть и нулевой), являющаяся
одновременно и границей полной расчетной схемы,
тогда как Г2— часть границы фрагмента, образуемая
при его выделении из полной конструкции и не
являющаяся границей полной конструкции.

16.

Краевые условия фрагмента на границе Г1
наследуют соответствующие краевые условия
полной конструкции на той же границе. Что касается
краевых условий на Г2, то здесь возможны
следующие три варианта. Постановка статических
краевых условий на Г2, постановка кинематических
краевых условий на Г2, постановка смешанных
краевых условий на Г2.

17.

Если на Г2 ставятся статические краевые условия, то
это означает, что к данной границе фрагмента
прикладываются в качестве внешних сил усилия
взаимодействия между фрагментом и отброшенной
частью полной конструкции — реакции, полученные
при отбрасывании остальной части конструкции.

18.

Если на Г2 ставятся кинематические краевые
условия, то эта граница полностью закрепляется от
всех смещений, а внешние воздействия на фрагмент
пополняются заданными на Г2 перемещениями,
величины которых определены ранее из расчета
загрубленной расчетной схемы.

19.

При смешанных краевых условиях вдоль границы
фрагмента Г2 прикладываются частично силовые,
частично кинематические внешние воздействия.

20.

Далее фрагмент рассчитывается с использованием
более детальной расчетной схемы, и из полученного
таким образом решения используется та часть,
которая относится к точкам, расположенным на
некотором удалении от границ фрагмента.

21.

Следует заметить, что при выделении из системы
фрагмента последний может оказаться изменяемым.
Если изменяемость является следствием самой
структуры фрагмента (внутренняя изменяемость), то
постановка чисто статических краевых условий на Г2
недопустима, и нужно переходить к кинематическим
или смешанным краевым условиям, сохраняющим
геометрическую неизменяемость фрагмента.

22.

Если же фрагмент внутренне неизменяем, но имеет
степени свободы твердого тела, то его следует
раскрепить статически определимым способом.

23.

Поскольку все внешние нагрузки, действующие на
фрагмент,
являются
само-уравновешенными
(рассматривается случай, когда граница Г1 или не
существует, или на ней поставлены статические
краевые условия), то при статически определимом
закреплении реакции в дополнительно наложенных
связях должны оказаться нулевыми.

24.

Это рассуждение верно лишь теоретически,
поскольку не учитывает неизбежную погрешность
численного решения. Накопление ошибок округления
приводит к тому, что вместо нулевой реакции мы
получаем малые, но все же ненулевые значения
реакций. Это свидетельствует о том, что в реальном
численном представлении дело обстоит так, как если
бы имела место некоторая небольшая ненулевая
сила, действующая на фрагмент.

25.

Поскольку упомянутая сила воспринимается условно
наложенными связями, то значения полученных
реакций оказываются зависящими от способа
наложения этих связей. Если такие связи
расположить, по возможности, далеко друг от друга,
реакции окажутся малыми и не внесут заметного
возмущения в напряженное состояние.

26.

В работе С.А. Алексеева (Качество статически
определимого прикрепления узлов и твердых тел //
Расчет пространственных конструкций.- Вып.17.- М.:
Стройиздат, 1977) рассматривался вопрос о
наилучшем, в смысле минимизации возможного
значения
реакций,
статически
определимом
закреплении тела.

27.

Было показано, что для плоского случая (закрепление
диска) наилучшим будет такое закрепление, при котором
треугольник, образованный линиями расположения
связей, является максимально возможным из всех,
описанных вокруг данного диска (рис. а). Ему
соответствует характеризующий качество закрепления
детерминант системы уравнений равновесия диска
относительно опорных реакций А = 1,673 d.

28.

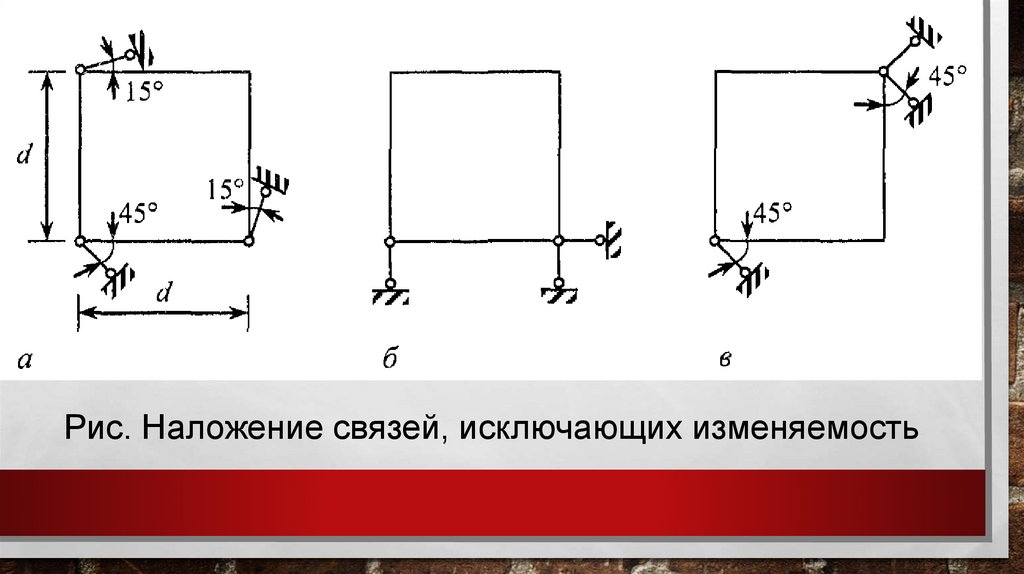
Рис. Наложение связей, исключающих изменяемость

29.

Для схемы по рис. б этот детерминант A = d, а для
схемы по рис. в он будет равным А = 1,414 d. Для
пространственного блока наибольшее возможное
значение детерминанта достигается в том случае,
когда на направлениях расположения связей можно
построить наибольший возможный параллелепипед,
описанный около блока.

30.

Сказанное относится к любому случаю раскрепления
системы, имеющей свободу перемещений, как жесткого
тела.
Максимизация
детерминанта
порождает
теоретически наиболее устойчивую систему уравнений
равновесия относительно усилий во введенных связях.
Для уменьшения погрешностей, накапливаемых при
формировании разрешающей системы уравнений,
целесообразно закреплять те узлы, которые приводят к
наименее податливой из раскрепленных внешними
связями конструкций.

31.

Нередко в инженерной практике фрагментация
оказывается полезным приемом, позволяющим
перейти от неограниченных областей, занимаемых
полной расчетной схемой, к ограниченным областям.
Типичный пример представляют собой задачи
расчета
балочных
и
плитных
конструкций,
покоящихся на упругом основании, когда в качестве
механической
модели
упругого
основания
принимается упругий слой конечной толщины.

32.

Рис. Фрагментация при замене неограниченного
упругого слоя слоем конечных размеров

33.

Чтобы применить программное обеспечение метода
конечных элементов, приходится ограничивать
размеры слоя в плане, пренебрегая работой той
части упругого основания, которая находится на
достаточном удалении от края конструкции. И
первый же вопрос, который возникает в связи с этим,
— насколько нужно отступить в упругом слое от края
конструкции, чтобы отдаленной частью упругого слоя
можно было пренебречь в расчетной схеме?

34.

Эмпирическое правило (оно также может быть
обоснованным
теоретически
с
привлечением
принципа
Сен-Венана
и
математического
инструментария теории упругости и пластичности),
известное опытным расчетчикам, говорит о том, что
вполне достаточно включить в расчетную схему
упругий слой, находящийся с каждой стороны от края
конструкции на расстоянии L=Н…1,5Н, где Н—
высота сжимаемой толщи.

35.

Оценку искажающего влияния такой фрагментации на
напряженное состояние конструкции можно получить
сопоставлением двух решений с различными краевыми
условиями по вертикальному разрезу упругого слоя. В
первом случае краевые условия по вертикальному
разрезу слоя принимаются статическими с нулевыми
внешними силами вдоль Г2. Во втором случае на Г2
принимаются
условия
полного
закрепления
от
смещений.

36.

Итак, принцип фрагментации, в отличие от
стратификации, основан на рассмотрении не всей
схемы, а отдельного фрагмента. Взаимодействие
фрагмента с остальной конструкцией заменяется
действием силовых или деформационных факторов
в местах примыкания отброшенной части.

37.

Конечно, значения этих факторов берутся из расчета
всей конструкции, схема которой может быть
достаточно (в пределах разумного) упрощенной, зато
сам фрагмент может быть сколь угодно сложен и
иметь даже другой тип конечно-элементной модели.
Например, общая схема может быть стержневой, а
фрагмент исследуемого узла может быть создан на
основе трехмерных конечных элементов.

38.

Безусловно, реализация принципа фрагментации
вручную очень трудоемка. Но если этот процесс
автоматизирован, то его эффективность трудно
переоценить. Так, в ПК МОНОМАХ, который
ориентирован
на
расчет
и
проектирование
конструкций высотных зданий, этот процесс
автоматизирован.

39.

После расчета всего каркаса здания совместно с
грунтовым и свайным основанием на все виды
воздействий
пользователь
может
выделить
необходимый для исследования фрагмент (плита
перекрытия, фундаментная плита, диафрагма) и
автоматически
получить
силовые
или
деформационные
воздействия
на
него
от
отброшенной части.

40.

Использование суперэлементов.
Идея применения суперэлементов известна давно, а
ее первые реализации, написанные на волне
супероптимистических ожиданий от преимуществ
суперэлементов, были осуществлены еще на
стареньких ламповых вычислительных машинах.
Как-то незаметно с течением времени практический
интерес разработчиков программ к суперэлементам
в значительной степени притупился.

41.

Это связано с фантастически быстрым ростом
мощности компьютеров как по быстродействию, так
и по объемам доступных ресурсов памяти, что, по
мнению
многих
разработчиков,
компенсирует
выигрыш от использования суперэлементов. Это не
всегда так. Представляется, что применение
суперэлементной модели полезно в нескольких
аспектах:

42.

• в качестве средства сокращения объема входной
информации;
• в качестве инструмента резкого понижения запросов
программы к потребляемым ресурсам компьютера;
• в качестве эффективного средства борьбы с потерей
точности расчета при высоких порядках матриц;
• в качестве удобного готового инструмента для
проведения статической конденсации к выделенным
узлам и выделенным им степеням свободы.

43.

Эта последняя возможность крайне полезна,
например, для последующего учета нелинейного
поведения конструкции, когда вся нелинейность
сосредоточена в этих выделенных узлах в
направлении выделенных степеней свободы.

44.

Все эти преимущества суперэлементной модели в
полной мере проявляются только в том случае, когда
в системе имеется много повторяющихся одинаковых
суперэлементов, у которых количество внутренних
узлов заметно превышает число внешних узлов, а
сами суперэлементы реализованы в программе с
достаточно
большим
допустимым
уровнем
вложенности,
образуя
развитую
иерархию
суперэлементов как типов элементов.

45.

Хорошая реализация суперэлементных моделей не
должна накладывать ограничений ни на внешние
воздействия,
которые
могут
различаться
у
конкретных представителей суперэлеменгов одного и
того же типа, ни на их взаимное пространственное
положение, в том числе суперэлементы одного типа
должны допускать различную ориентацию по
отношению к глобальной системе координат.

46.

Принцип
суперэлементов
ориентирован
на
преодоление большой размерности задачи. Однако
он это делает не за счет применения набора
упрощенных схем всей конструкции или набора
вложенных расчетных схем (фрагментация), а за
счет суперэлементной рекурсии, т.е. общая схема
конструкции может быть очень подробной и включать
несколько миллионов узловых неизвестных.

47.

Суперэлементы могут как представлять собой часть
конструкции (плита перекрытия, диафрагма, купол и
т.п.), так и являться «вложенной» схемой. Например, при
расчете оболочки контаймента на обжатие системой
канатов удобно использовать три типа суперэлементов:
купол, цилиндрическая часть, система канатов
(вложенная
схема).
Применение
суперэлементов
полезно не только для преодоления размерности
решаемой задачи, но и для удобства синтеза и анализа.

48.

Суперэлементный подход особенно эффективен,
когда расчленение на подсистемы происходит
естественно: например, здание из объемных блоков
(объемный блок — суперэлемент) или диафрагма
высотного здания, собирающаяся из отдельных
панелей (панель — суперэлемент), соединяющихся
между собой в угловых точках.

49.

Рис. Фрагмент
диафрагмы
высотного здания

50.

Расчет такой системы можно выполнить обычным
способом нанести необходимую сетку и рассчитать
всю систему целиком. Однако большое количество
расчетных
узлов,
элементов,
неизвестных
перемещений может сильно затруднить решение
задачи. Используя суперэлеменгы, можно провести
расчет поэтапно, существенно снизив на каждом
этапе размерность задачи.

51.

Сначала построить матрицу жесткости для всех
типов суперэлементов [в данном случае имеются два
типа], затем рассчитать систему, состоящую из
суперэлементов (в данном случае система будет
состоять из 6 суперэлементов с 12 суперузлами). В
результате этого расчета будут определены
перемещения суперузлов. На заключительном этапе
рассчитать каждый из шести суперэлементов на
заданные перемещения суперузлов.

52.

Рис. Типы суперэлементов для рассматриваемого
фрагмента диафрагмы высотного здания

53.

Последовательность расчета системы, набранной из
суперэлементов, аналогична приведенной ранее с
той лишь разницей, что матрица жесткости и
узловые нагрузки определяются в результате
расчета.

54.

Так как суперэлемент представляет сам по себе
достаточно сложную систему, то матрицы базовых
функций φс строятся при помощи численного
расчета суперэлемента на единичные смещения
суперузлов, в результате которого строится матрица
влияния, связывающая перемещения внутренних
узлов суперэлемента с единичными смещениями
суперузлов.

55.

Такая
процедура
обработки
суперэлементов
позволяет представить метод суперэлементной
рекурсии как расчет по методу конечных элементов с
построением аппроксимирующих функций при
помощи матриц влияния.

56.

Другая процедура обработки суперэлементов основана
на том, что в физическом смысле исключения j-го
неизвестного по Гауссу соответствует освобождению от
j-й связи. Это приводит к такой схеме построения
матрицы жесткости и сведению местной нагрузки к
узловой: для i-го суперэлемента вначале нумеруются
все внутренние узлы (соответствующее им число
степеней свободы обозначим ni), а затем суперузлы
(количество
степеней
свободы,
соответствующее
суперузлам, обозначим ni0).

57.

Составляются канонические уравнения для всех
ni + ni0 степеней свободы; исключаются ni
неизвестные; оставшиеся части матрицы и столбцов
свободных членов (на рис. они заштрихованы)
образуют искомые матрицы жесткости и столбцы
узловых нагрузок.

58.

Рис. Исключение ni неизвестных и образование искомых
матриц жесткости и столбцов узловых нагрузок

59.

С
точки
зрения
этой
процедуры
метод
суперэлементной рекурсии можно трактовать как
своеобразный блочный метод Гаусса.
С точки зрения строительной механики и метода
конечных элементов такой подход можно трактовать
как применение в расчете алгоритмических конечных
элементов, для которых матрица жесткости и
приведение
местной
нагрузки
к
узловой
осуществляется численными методами.

60.

Т.о., суперэлементный подход позволяет значительно
сократить количество вычислений. Влияние плохой
обусловленности общей матрицы систем уравнении
преодолевается за счет того, что при наличии
одинаковых типов КЭ погрешность локализуется.
Используя физический смысл матрицы жесткости (МЖ)
суперэлемента, можно выбрать элементы, сумма
которых должна быть равна нулю, или составить
уравнение равновесия относительно оси, проходящей
через любые два суперузла, и т.п.

61.

На
основе
различных
предпосылок
можно
«подправить» элемент МЖ, полностью исключив
погрешность, накопленную в процессе исключения
неизвестных
перемещений
внутренних
узлов
суперэлемента. По такой же процедуре может быть
обработан и столбец супернагрузок.

62.

Метод суперэлементов может оказаться очень
удобным при решении нелинейных задач, когда
существуют
подконструкции,
которые
можно
рассматривать как линейные. Например, здания
большой жесткости на податливых односторонних
связях. В этом случае схема здания может быть
объявлена
суперэлементом,
и
итерационный
процесс решения нелинейной задачи будет сведен к
расчету небольшой основной системы.

63.

Второй пример — задача расчета здания на
нелинейно-деформированном грунтовом основании
может
быть
решена
следующим
образом:
конструкции
всего
здания
объявляются
суперэлементом, а нелинейная часть принимается в
качестве
основной системы. Это
позволяет
значительно сократить время решения нелинейной
задачи.

64.

Таким образом, реализация методов решения
разреженных матриц совместно с суперэлементным
в
настоящее
время
является
наиболее
эффективным инструментарием, так как дает
возможность:

65.

• значительно сократить количество вычислений, а
следовательно, и время решения задачи;
• достаточно успешно решить проблему плохой
обусловленности матрицы больших систем уравнений;
• организовать
задач;
эффективное
решение
нелинейных
• удобно осуществить синтез компьютерных моделей, т.к.
на этапе создания расчетных схем работа с
суперэлементами обладает теми же удобствами, что и
работа с фрагментами.

66.

Определенным недостатком суперэлементного подхода
является трудность реализации, связанная не только с
организацией рекурсивного расчета, но и организацией
пользовательского интерфейса. Так, визуализация
результатов расчета (изополей усилий и напряжений)
для всей конструкции, состоящей из суперэлементов,
связана со значительными трудностями. Этим можно
объяснить, что суперэлементный подход реализован
только
в
наиболее
продвинутых
программных
комплексах.

67.

Как и рассмотренные выше приемы, принцип
суперэлементов ориентирован на преодоление
большой размерности задачи. Однако он это делает
не за счет применения набора упрощенных схем
всей конструкции или набора вложенных расчетных
схем (фрагментация), а за счет суперэлементной
рекурсии, т. е. общая схема конструкции может быть
очень подробной и включать несколько миллионов
узловых неизвестных.