Многофазная сортировка файлов

1.

п3. Многофазная сортировка файлов
(Также «совершенная» или «идеальная»).
Автор – Р. Гилстэд, 1960г.
Пусть имеется исходный файл f и три рабочих файла – f0, f1,
f2. В качестве основы возьмём следующий алгоритм:
1. Копируем содержимое исходного файла f в f2. Создадим
указатели fi, fj, fk, которые смотрят на f0, f1, f2 соответственно.
2. Разобьём файл fk в fi и fj (как в сортировках естественного
слияния). Перенаправим указатель fk на файл f2;
3. Сольём отрезки из fi и fj в fk, при этом возможны два исхода:
3.1. В fi или fj остались отрезки (пусть в fi) – тогда обмениваем
значения указателя fk с тем, указателем, который смотрит на
пустой файл и переходим к п.3 (т.о., fk опять смотрит на
пустой файл, а fi, fj на файлы с отрезками);
3.2. Если последовательность в fk не упорядочена полностью,
переходим к п.2, иначе задача решена.

2.

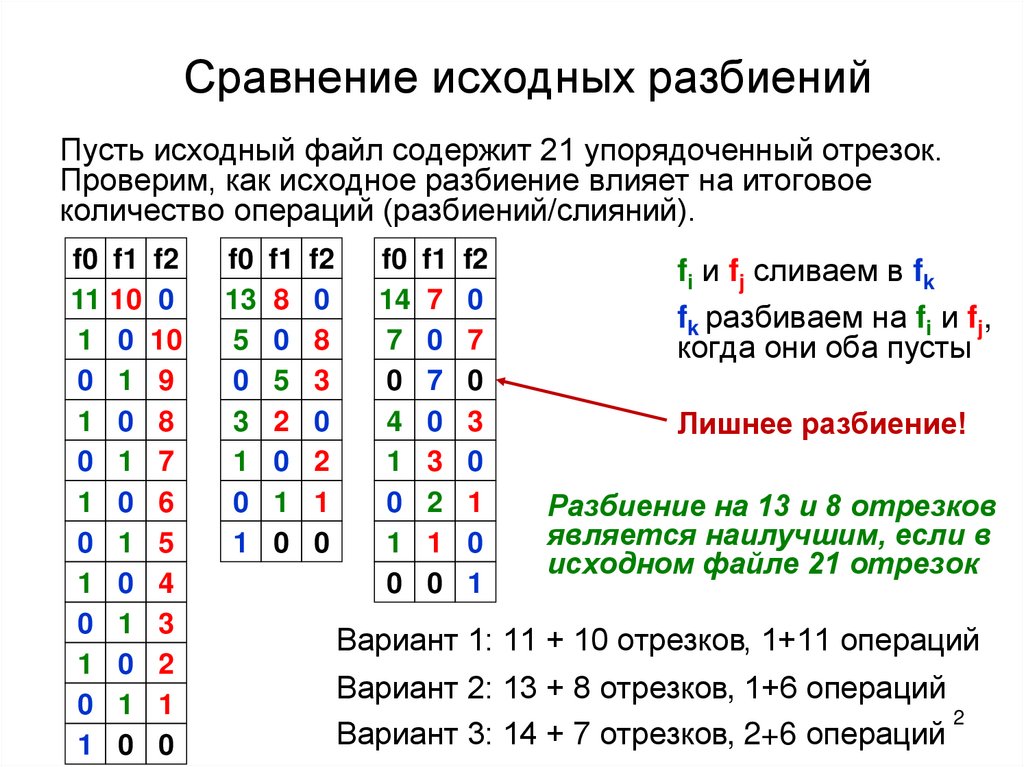
Сравнение исходных разбиений
Пусть исходный файл содержит 21 упорядоченный отрезок.
Проверим, как исходное разбиение влияет на итоговое
количество операций (разбиений/слияний).
f0 f1 f2
11 10 0
1 0 10
0 1 9
1 0 8
0 1 7
1 0 6
0 1 5
1 0 4
0 1 3
1 0 2
0 1 1
1 0 0
f0 f1 f2
13 8 0
5 0 8
0 5 3
3 2 0
1 0 2
0 1 1
1 0 0
f0 f1 f2
14 7 0
7 0 7
0 7 0
4 0 3
1 3 0
0 2 1
1 1 0
0 0 1
fi и fj сливаем в fk
fk разбиваем на fi и fj,
когда они оба пусты
Лишнее разбиение!
Разбиение на 13 и 8 отрезков
является наилучшим, если в
исходном файле 21 отрезок
Вариант 1: 11 + 10 отрезков, 1+11 операций
Вариант 2: 13 + 8 отрезков, 1+6 операций
2
Вариант 3: 14 + 7 отрезков, 2+6 операций

3.

Идеальное разбиение
Просуммируем число отрезков на каждом этапе нашего
«идеального разбиения»:
f0 f1 f2
13 8 0
5 0 8
0 5 3
3 2 0
1 0 2
0 1 1
1 0 0
21
13
8
5
3
2
1
1, 2, 3, 5, 8, 13, 21, …
Ничего не напоминает?
Числа Фибоначчи
3

4.

Идеальное разбиение
Как же идеальное число отрезков в файлах
связано с числами Фибоначчи?
0, 1, 1, 2, 3, 5, 8, 13, 21, …
сумма двух
0, 1, 1, 2, ..
1
0, 1, 1, 2, 3, 5, …
2
0, 1, 1, 2, 3, 5, 8, …
3
0, 1, 1, 2, 3, 5, 8, 13, …
5
0, 1, 1, 2, 3, 5, 8, 13, 21, … 8
0, 1, 1, 2, 3, 5, 8, 13, 21, … 13
сумма двух без первого
1
1
2
3
5
8
….
4

5.

Идеальное разбиение
Идеальное число отрезков в файлах – это
последовательные
частичные
суммы
чисел
Фибоначчи.
Количество суммируемых чисел – это количество
файлов для разбиения. В нашем примере это два
файла, третий использовался для слияния.
Числа Фибоначчи fib(1), fib(2), fib(3)… порядка N
определяются по формулам:
fib(i) = 0, 1≤ i ≤ N-1
fib(N) = 1,
fib(k) = fib(k – 1) + fib(k – 2) + … + fib(k – N), k > N
5

6.

Идеальное разбиение
Построим ряд 5-го порядка:
0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 31, 61, 120, 236
Начальный отрезок
Каждое последующее =
сумме 5 предыдущих
Подсчитаем частичные суммы для ряда Фибоначчи:
0, 0, 0, 0, 1
1 1 1 1 1 Суммы последних пяти, четырёх, трёх,
двух и одного члена последовательности
0, 0, 0, 1, 1
22221
0, 0, 1, 1, 2
44432
………
1, 2, 4, 8,16
31 30 28 24 16
6

7.

Описание процедуры разбиения
На каждом уровне разбиения будут
выполняться действия:
1. Вычисление очередных частичных сумм
чисел Фибоначчи – массив ip (ideal partition);
2. Определение, сколько надо добавить в
каждый файл к предыдущему разбиению –
массив ms (missing segments);
3. Дополнение файлов этим количеством
отрезков;
4. Повторение с п.1, если файл еще не
закончился.
Отрезки не должны сливаться – ограничим их
7
числом -1.

8.

Пример: процедура разбиения
Исходный файл f0: 5 12 4 3 7 8 5 9 6 3 15 18 20 10 11 1 2
Этап 1:
f[0]:
f[1]:
id ms
1 1
1 1
f[0]: 5 12 -1
f[1]:
1
1
0
1
f[0]: 5 12 -1
f[1]: 4 -1
1
1
0
0
0, 1, 1, 2, 3, 5, 8, 13, 21, …
Частичные суммы (N = 2):
11 21 32 53 85
На каждом этапе
добавляем отрезки
в соответствующий
файл, пока не
покроем
потребность
8

9.

Пример: процедура разбиения
Исходный файл f0: 5 12 4 3 7 8 5 9 6 3 15 18 20 10 11 1 2
Этап 2:
f[0]: 5 12 -1
f[1]: 4 -1
id ms
2 1
1 0
f[0]: 5 12 -1 3 7 8 -1
f[1]: 4 -1
2
1
0, 1, 1, 2, 3, 5, 8, 13, 21, …
Частичные суммы (N = 2):
11 21 32 53 85
На каждом этапе
добавляем отрезки
в соответствующий
файл, пока не
покроем
потребность
0
0
9

10.

Пример: процедура разбиения
Исходный файл f0: 5 12 4 3 7 8 5 9 6 3 15 18 20 10 11 1 2
Этап 3:
f[0]: 5 12 -1 3 7 8 -1
f[1]: 4 -1
id ms
3 1
2 1
f[0]: 5 12 -1 3 7 8 -1 5 9 -1
f[1]: 4 -1
3
2
0
1
f[0]: 5 12 -1 3 7 8 -1 5 9 -1
f[1]: 4 -1 6 -1
3
2
0
0
0, 1, 1, 2, 3, 5, 8, 13, 21, …
Частичные суммы (N = 2):
11 21 32 53 85
На каждом этапе
добавляем отрезки
в соответствующий
файл, пока не
покроем
потребность
10

11.

Пример: процедура разбиения
Исходный файл f0: 5 12 4 3 7 8 5 9 6 3 15 18 20 10 11 1 2
Этап 4:
f[0]: 5 12 -1 3 7 8 -1 5 9 -1
f[1]: 4 -1 6 -1
id ms
5 2
3 1
f[0]: 5 12 -1 3 7 8 -1 5 9 -1 3 15 18 20 -1 10 11 -1
f[1]: 4 -1 6 -1
5
3
0
1
f[0]: 5 12 -1 3 7 8 -1 5 9 -1 3 15 18 20 -1 10 11 -1
f[1]: 4 -1 6 -1 1 2 -1
5
3
0
0
0, 1, 1, 2, 3, 5, 8, 13, 21, …
Частичные суммы (N = 2):
11 21 32 53 85
Итого: 4 этапа – столько
же будет слияний!
11

12.

Пример: процедура слияния
Прежде чем перейти к процедуре слияния, посмотрим ещё
раз на пример с идеальным разбиением 21 отрезка из начала:
f0 f1 f2
13 8 0 Сливаем по 8 отрезков в f2
5 0 8 Сливаем по 5 отрезков в f1
0 5 3 Сливаем по 3 отрезка в f0
3 2 0 Сливаем по 2 отрезка в f2
1 0 2 Сливаем по 1 отрезку в f1
0 1 1 Сливаем по 1 отрезку в f0
1 0 0 Результат сортировки в f0
Обратите внимание на
цикличность в индексе файла
для слияния. Этим можно
воспользоваться, сдвигая
указатели на файлы так,
чтобы слияние происходило
всегда в один и тот же
указатель (например, f2).
12

13.

Пример: процедура слияния
Этап 1 (пока f[1] не опустеет):
f[0]: 5 12 -1 3 7 8 -1 5 9 -1 3 15 18 20 -1 10 11 -1
f[1]: 4 -1 6 -1 1 2 -1
f[2]: 4 5 12 -1 3 6 7 8 -1 1 2 5 9 -1
f[1] закрываем на чтение, открываем на запись;
f[2] закрываем на запись, открываем на чтение;
Сдвигаем указатели:
FILE *tmp = f[2];
f[2] = f[1];
f[1] = f[0];
f[0] = tmp;
13

14.

Пример: процедура слияния
Этап 2 (пока f[1] не опустеет):
f[0]: 4 5 12 -1 3 6 7 8 -1 1 2 5 9 -1
f[1]: 5 12 -1 3 7 8 -1 5 9 -1 3 15 18 20 -1 10 11 -1
Было прочитано на этапе 1
f[2]: 3 4 5 12 15 18 20 -1 3 6 7 8 10 11 -1
f[1] закрываем на чтение, открываем на запись;
f[2] закрываем на запись, открываем на чтение;
Сдвигаем указатели:
FILE *tmp = f[2];
f[2] = f[1];
f[1] = f[0];
f[0] = tmp;
14

15.

Пример: процедура слияния
Этап 3 (пока f[1] не опустеет):
f[0]: 3 4 5 12 15 18 20 -1 3 6 7 8 10 11 -1
f[1]: 4 5 12 -1 3 6 7 8 -1 1 2 5 9 -1
f[2]: 1 2 3 4 5 5 9 12 15 18 20 -1
Закрываем/открываем f[1] и f[2], сдвигаем указатели…
Этап 4 (пока f[1] не опустеет):
f[0]: 1 2 3 4 5 5 9 12 15 18 20 -1
f[1]: 3 4 5 12 15 18 20 -1 3 6 7 8 10 11 -1
f[2]: 1 2 3 3 4 5 5 6 7 8 9 10 11 12 15 18 20 -1
Результат всегда в f[n-1] (или в f[0] после сдвига указателей) 15

16.

Идеальное разбиение: как получить?
Число отрезков в исходном файле может быть
неподходящим для идеального разбиения.
Вопрос: что делать в этом случае?
Ответ: просто добавить воды пустые (фиктивные) отрезки!
Количество пустых отрезков можно хранить в массиве ms.
Прежде чем брать числа для слияния из файла f[i],
проверить наличие пустого отрезка в ms[i] и уменьшить
ms[i]--, тем самым имитируя слияние пустого отрезка
из файла f[i] раньше других его отрезков .
16

17.

Пример с фиктивным отрезком
Исходный файл f0: 5 12 4 3 7 8 5 9 6 3 15 18 20 10 11
Этап 4:
f[0]: 5 12 -1 3 7 8 -1 5 9 -1
f[1]: 4 -1 6 -1
Отрезков 7, а не 8!
На первых трёх
этапах это не
скажется, так что
пропустим их
id ms
5 2
3 1
f[0]: 5 12 -1 3 7 8 -1 5 9 -1 3 15 18 20 -1 10 11 -1
f[1]: 4 -1 6 -1
5
3
0
1
f[0]: 5 12 -1 3 7 8 -1 5 9 -1 3 15 18 20 -1 10 11 -1
f[1]: 4 -1 6 -1 -1
5
3
0
1
0, 1, 1, 2, 3, 5, 8, 13, 21, …
Частичные суммы (N = 2):
11 21 32 53 85
В файле f[1] – один
фиктивный (пустой)
отрезок (ms = 1)
17

18.

Вычисление чисел ip и ms
Как мы видели ранее, первоначальные значения частичных
сумм чисел Фибоначчи всегда равны 1:
ip[i] = 1, i = 0, 1,..., N-1
Следовательно, количества отрезков, которые надо
добавить в первый раз в файлы, также равны 1:
ms[i] = 1, i = 0, 1,..., N-1
Выведем формулы вычисления ip и ms для следующего
уровня разбиения, не используя ряд Фибоначчи явно и не
храня предыдущие значения чисел ip[i].
18

19.

Вычисление чисел ip
Пусть текущие числа Фибоначчи порядка n = 3 равны
fib1, fib2, fib3, ..., тогда частичные суммы равны:
Т.к. fib1 = 0,
ip[0] = fib1 + fib2 + fib3
fib4 = 0 + fib2 + fib3 = ip[0]
ip[1] = fib2 + fib3
ip[2] = fib3
fib1, fib2, fib3, fib4, ... – следующая группа чисел, тогда:
ip[0]след = fib2 + fib3 + fib4 = fib2 + fib3 + ip[0] = ip[1] + ip[0];
ip[1]след = fib3 + fib4 = ip[2] + ip[0];
ip[2]след = fib4 = 0 + ip[0] = пусть ip[n] ≝ 0 = ip[3] + ip[0];
Отсюда, для ip0 = ip[0], ip[n] = 0,
ip[k]след = ip[k+1] + ip0; k = 0, .., n-1
(1)
19

20.

Вычисление чисел ms
Пусть текущие числа Фибоначчи порядка n = 3 равны
fib1, fib2, fib3, ..., тогда частичные суммы равны:
ip[0]след = fib2 + fib3 + fib4
ip[0] = fib1 + fib2 + fib3
ip[1]след = fib3 + fib4
ip[1] = fib2 + fib3
ip[2]след = fib4
ip[2] = fib3
fib1, fib2, fib3, fib4, ... – следующая группа чисел, тогда:
ms[0] = ip[0]след – ip[0] = fib2 + fib3 + fib4 – ip[0] =
= fib4 = ip[0] = ip[1] – ip[0] + ip[0];
ms[1] = ip[1]след – ip[1] = fib3 + fib4 – ip[1] =
= fib4 = ip[0] = ip[2] – ip[1] + ip[0]; ………
Отсюда,
ms[k] = ip[k+1] - ip[k] + ip[0]; k = 0, .., n-1
(2) 20

21.

Вычисление чисел ip и ms
Таким образом, выведенные формулы позволяют не
вычислять сам ряд Фибоначчи, а получать новые значения
массивов ip и ms из предыдущих («старых») значений
массива ip по соотношениям (1), (2), задав только
начальные значения:
ms[0] = ms[1] = … = ms[n - 1] = 1, ms[n] = 0;
ip[0] = ip[1] = … = ip[n - 1] = 1, ip[n] = 0;
Заметим, что сначала будем вычислять массив ms, а
потом ip.
21

22.

Пример
ip0
ms: 1 1 1 1 1 0
ip: 1 1 1 1 1 0
1
ms: 1 1 1 1 0 0
ip: 2 2 2 2 1 0
2
ms: 2 2 2 1 1 0
ip: 4 4 4 3 2 0
n=5+1
ip0 = ip[0]; // старое значение ip[0]
ms[k] = ip[k+1] - ip[k] + ip0; k = 0, .., n-1
ip[k]след = ip[k+1] + ip0, для k = 0,1,..., n-1
22

23.

Алгоритм многофазной сортировки
А точнее, «Алгоритм сортировки файла многофазным
слиянием с использованием горизонтального
распределения отрезков»
Этап 1. Разбиение исходного файла на n - 1 рабочий
файл по отрезкам с соблюдением идеального разбиения.
Этап 2. Слияние.
23

24.

Алгоритм многофазной сортировки
n – число рабочих файлов,
f[0], f[1],…, f[n-1] – рабочие файлы,
L - счетчик уровней,
ip[0], ip[1],…, ip[n-1] – идеальное распределение отрезков
на каждом уровне,
ms[0], ms[1],…, ms[n-1] –
на этапе 1: число отрезков, необходимое для перехода от
одного идеального распределения к другому,
на этапе 2: число фиктивных отрезков в каждом рабочем
файле
24

25.

Этап 1 - разбиение
1.
2.
Начальные установки.
f[0], f[1],.., f[n-2] открыть на запись,
fисходный открыть на чтение,
ip[0] = ip[1] =…= ip[n-2] = 1, ip[n-1] = 0.
ms[0] = ms[1] =…= ms[n-2] = 1, ms[n-1] = 0.
L = 1, i = 0.
Записать очередной отрезок из исходного файла в
файл с номером i.
ms[i]--.
Если исходный файл исчерпан, закрыть все файлы и
перейти к шагу 5, иначе к 3.
25

26.

Этап 1 - разбиение
3.
4.
Если ms[i] < ms[i+1], то i++ и перейти на 2,
иначе
если ms[i] == 0, то перейти на 4,
иначе i = 0 и перейти на 2.
Пересчёт уровня и значений в массивах ip и ms:
L++, ip0 = ip[0], i = 0;
Пункт №3 нужен для
для k = 0, 1,.., n-2
равномерного
распределения
ms[k] = ms[k+1] - ip[k] + ip0,
фиктивных отрезков
ip[k] = ip[k+1] + ip0;
по рабочим файлам
Перейти на 2.
26

27.

Распределение фиктивных отрезков
Пусть n = 5 + 1
ip: 08 08 07 06 04 00
ip: 16 15 14 12 08 00
на уровне 4
на уровне 5
ms: 08 07 07 06 04 00
∑ = 32
Если отрезков в файле >= 32, то нам их хватит для каждого
файла и безразлично, как распределять. «Счастье для
всех, даром, и пусть никто не уйдет обиженный!»
Но если их < 32, например 22, то в файлах будет 10
фиктивных отрезков. «Потому что всех много, а всего –
мало!»
27

28.

Распределение фиктивных отрезков
Варианты распределения отрезков:
1. Последовательно по файлам:
8 в первый (осталось 14), по 7 во второй (осталось 7) и
третий и … отрезки закончились. Тогда:
ms: 08 07 07 06 04
реальных отрезков: 08 07 07 00 00
фиктивных отрезков: 00 00 00 06 04
28

29.

Распределение фиктивных отрезков
2. Распределение отрезков в файлы поочередно :
1 -> 2 -> 3 -> 4 -> 5 -> 1 -> 2 -> 3 -> 4 -> 5 -> …
Тогда количество фиктивных отрезков будет по 22 / 5 = 4
отрезка в каждом и, т.к. 22 % 5 = 2, то в первых двух
файлах по 5 отрезков:
ms: 08 07 07 06 04
реальных отрезков: 05 05 04 04 04
фиктивных отрезков: 03 02 03 02 00
29

30.

3. Горизонтальное распределение отрезков
3. Если ms[i] < ms[i + 1], то i++ и перейти на 2,
иначе
если ms[i] == 0, то перейти на 4 (пересчет ip и ms),
иначе (ms[i] >= ms[i+1]) i = 0 и перейти на 2.
f: 1
2
3
4
5
- номера файлов
ms: 07 07 07 06 04 00 ms[0] == ms[1], i=0
1
2
3
4
5
6
7
06 06 06 06 04 00 ms[2] == ms[3], i=0
8
05 05 05 05 04 00 ms[3] > ms[4], i=0
9 10 11 12
04 04 04 04 04 00 ms[3] == ms[4], i=0
13 14 15 16 17
Далее отрезки будут распределяться
поочередно по одному по всем файлам.
И если реальных отрезков было 12, то во
всех файлах будет по 4 фиктивных отрезка,
а если 22, то по 2.
18 19 20 21 22
23 24 25 26 27
28 29 30 31 32
30

31.

Этап 2 – слияние
5. f[0], f[1],.., f[n-2] открыть на чтение, f[n-1] - на запись,
6. Если L = 0, то сортировка завершена, результат в f[0].
7. Сливать отрезки из f[0], f[1],…, f[n-2] в f[n-1] пока не
исчерпается f[n-2] (ip[n-2] обратится в 0):
7.1. Пока все ms[i] > 0 (т.е. во всех файлах есть
фиктивные отрезки), все ms[i]-- (i = 0, 1,…, n-2), а ms[n-1]++
(т.е. появился фиктивный отрезок в f[n-1])
7.2. Сливать по одному отрезку из каждого f[i], для
которого ms[i] == 0 и уменьшать на 1 ms[i], если ms[i] > 0
(в i-ом файле фиктивный отрезок).
8. L-- . Закрыть файлы f[n-2] и f[n-1]. Открыть f[n-2] на
запись, f[n-1] на чтение. Передвинуть указатели на файлы и
их имена, массивы ip и ms. Перейти к 6.
31

32.

Этап 2 – слияние
При сдвиге последний элемент становится первым:
f[0], f[1], …, f[n-2], f[n-1] f[n-1], f[0], …, f[n-2]
Аналогично для имён файлов и массивов.
Замечание. Массив ip с числами Фибоначчи можно не
использовать – следить по концу файла f[n-2], а
использовать его для упорядочения отрезков
Результат сортировки остаётся в файле f[n-1] до сдвига
указателей или в f[0] после сдвига указателей.
32

33.

Замечания
1. Массив ip можно использовать для слияния упорядоченно
отрезков из файлов так же, как предлагалось в многопутевом
слиянии файлов.
2. При использовании файловых потоков (fstream) надо задавать
динамический массив указателей (присвоения в fstream нет – а
значит, перезаписывать сами объекты при сдвиге не получится)
на файлы, а затем открывать их конструктором или операцией
open:
std::fstream **files = new std::fstream *[fileCount];
for (int i = 0; i < fileCount; i++)
files[i] = new std::fstream(fileNames[i], std::ios::out);
3. При сдвиге указателей на файлы надо сдвигать и указатели
на их имена.
33

34.

Пример 1 (разбиение)
f: 20 15 27 13 25 12 1 15 23 2 24 6, n = 4 = 3 + 1
1. ip[0] = ip[1] =…= ip[n-2] = 1, ip[n-1] = 0.
ms[0] = ms[1] =…= ms[n-2] = 1, ms[n-1] = 0.
L = 1, i = 0
2. Записать очередной отрезок из исходного
файла в файл с номером i.
ms[i]--.
Если исходный файл исчерпан, закрыть
L: 2
все файлы и перейти к шагу 5, иначе к 3.
ms: 1 1 0 0
3. Если ms[i] < ms[i+1], то i++ и перейти на 2,
ip: 2 2 1 0
иначе если ms[i] == 0, то перейти на 4,
иначе i = 0 и перейти на 2.
2 -> 3.1 -> 2 -> 3.2 -> 4
4. Пересчет уровня, и значений в массивах ip
и ms.
f1: 20 -1 12 -1
L++, ip0 = ip[0], i = 0;
для k = 0,1,.., n-2
f2: 15 27 -1 1 15 23 -1
ms[k] = ip[k+1] - ip[k] + ip0,
f3: 13 25 -1 0, 0, 1, 1, 2, 3, 5, 8, 13, …
ip[k] = ip[k+1] + ip0;
Перейти на 2.
Частичные суммы:
L: 1
ms: 1 1 1 0
ip: 1 1 1 0
2 -> 3.1 -> 2 -> 3.1 -> 2 -> 3.2 -> 4
111 221 432 653
34

35.

Пример 1 (разбиение)
f: 20 15 27 13 25 12 1 15 23 2 24 6, n = 4 = 3 + 1
L: 3
ms: 2 1 1 0
ip: 4 3 2 0
2 -> 3.3 -> 2 -> 5
ms: 0 1 1 0
f1: 20 -1 12 -1 2 24 -1 6 -1
f2: 15 27 -1 1 15 23 -1
f3: 13 25 -1
1. ip[0] = ip[1] =…= ip[n-2] = 1, ip[n-1] = 0.
ms[0] = ms[1] =…= ms[n-2] = 1, ms[n-1] = 0.
L = 1, i = 0
2. Записать очередной отрезок из исходного
файла в файл с номером i.
ms[i]--.
Если исходный файл исчерпан, закрыть
все файлы и перейти к шагу 5, иначе к 3.
3. Если ms[i] < ms[i+1], то i++ и перейти на 2,
иначе если ms[i] == 0, то перейти на 4,
иначе i = 0 и перейти на 2.
4. Пересчет уровня, и значений в массивах ip
и ms.
L++, ip0 = ip[0], i = 0;
для k = 0,1,.., n-2
ms[k] = ip[k+1] - ip[k] + ip0,
ip[k] = ip[k+1] + ip0;
Перейти на 2.
35

36.

Пример 1 (слияние)
L = 3, ms: 0 1 1 0 -> 0 0 0 0
f1: 20 -1 12 -1 2 24 -1 6 -1
f2: 15 27 -1 1 15 23 -1
f3: 13 25 -1
7 -> 7.2 -> 7 -> 7.2 -> 7 -> 8
f4: 20 -1 12 13 15 25 27 -1
L = 2, ms: 0 0 0 0
f1: 20 -1 12 13 15 25 27 -1
f2: 20 -1 12 -1 2 24 -1 6 -1
f3: 15 27 -1 1 15 23 -1
7 -> 7.2 -> 7 -> 8
f4: 1 2 15 20 23 24 -1
6. Если L = 0, то сортировка
завершена, результат в f[0].
7. Сливать отрезки из f[0], f[1],…, f[n-2]
в f[n-1] пока не исчерпается f[n-2]:
7.1. Пока все ms[i] > 0, все ms[i]--, а
ms[n-1]++
7.2. Сливать по одному отрезку из
каждого f[i], для которого ms[i] == 0
и уменьшать на 1 ms[i],
если ms[i] > 0.
8. L-- . Закрыть файлы f[n-2] и f[n-1].
Открыть f[n-2] на запись, f[n-1] на
чтение. Передвинуть указатели на
файлы и их имена, массивы ip и ms.
Перейти к 6.
36

37.

Пример 1 (слияние)
L = 1, ms: 0 0 0 0
f1: 1 2 15 20 23 24 -1
f2: 20 -1 12 13 15 25 27 -1
f3: 20 -1 12 -1 2 24 -1 6 -1
7 -> 7.2 -> 7 -> 8
f4: 1 2 6 12 13 15 15 20 23 24 25 27 -1
6. Если L = 0, то сортировка
завершена, результат в f[0].
7. Сливать отрезки из f[0], f[1],…, f[n-2]
в f[n-1] пока не исчерпается f[n-2]:
7.1. Пока все ms[i] > 0, все ms[i]--, а
ms[n-1]++
7.2. Сливать по одному отрезку из
каждого f[i], для которого ms[i] == 0
и уменьшать на 1 ms[i],
если ms[i] > 0.
8. L-- . Закрыть файлы f[n-2] и f[n-1].
Открыть f[n-2] на запись, f[n-1] на
чтение. Передвинуть указатели на
файлы и их имена, массивы ip и ms.
Перейти к 6.
37

38.

Пример 2 (разбиение)
f: 28 3 20 16 3 5 2 5 1 2, n = 4 = 3 + 1
1. ip[0] = ip[1] =…= ip[n-2] = 1, ip[n-1] = 0.
ms[0] = ms[1] =…= ms[n-2] = 1, ms[n-1] = 0.
L = 1, i = 0
2. Записать очередной отрезок из исходного
файла в файл с номером i.
ms[i]--.
Если исходный файл исчерпан, закрыть
L: 2
все файлы и перейти к шагу 5, иначе к 3.
ms: 1 1 0 0
3. Если ms[i] < ms[i+1], то i++ и перейти на 2,
ip: 2 2 1 0
иначе если ms[i] == 0, то перейти на 4,
иначе i = 0 и перейти на 2.
2 -> 3.1 -> 2 -> 4
4. Пересчет уровня, и значений в массивах ip
и ms.
f1: 28 -1 3 5 -1
L++, ip0 = ip[0], i = 0;
для k = 0,1,.., n-2
f2: 3 20 -1 2 5 -1
ms[k] = ip[k+1] - ip[k] + ip0,
f3: 16 -1
0, 0, 1, 1, 2, 3, 5, 8, 13, …
ip[k] = ip[k+1] + ip0;
Перейти на 2.
Частичные суммы:
L: 1
ms: 1 1 1 0
ip: 1 1 1 0
2 -> 3.1 -> 2 -> 3.1 -> 2 -> 3.2 -> 4
111 221 432 653
38

39.

Пример 2 (разбиение)
f: 28 3 20 16 3 5 2 5 1 2, n = 4 = 3 + 1
L: 3
ms: 2 1 1 0
ip: 4 3 2 0
2 -> 5
ms: 1 1 1 0
f1: 28 -1 3 5 -1 1 2 -1
f2: 3 20 -1 2 5 -1
f3: 16 -1
1. ip[0] = ip[1] =…= ip[n-2] = 1, ip[n-1] = 0.
ms[0] = ms[1] =…= ms[n-2] = 1, ms[n-1] = 0.
L = 1, i = 0
2. Записать очередной отрезок из исходного
файла в файл с номером i.
ms[i]--.
Если исходный файл исчерпан, закрыть
все файлы и перейти к шагу 5, иначе к 3.
3. Если ms[i] < ms[i+1], то i++ и перейти на 2,
иначе если ms[i] == 0, то перейти на 4,
иначе i = 0 и перейти на 2.
4. Пересчет уровня, и значений в массивах ip
и ms.
L++, ip0 = ip[0], i = 0;
для k = 0,1,.., n-2
ms[k] = ip[k+1] - ip[k] + ip0,
ip[k] = ip[k+1] + ip0;
Перейти на 2.
39

40.

Пример 2 (слияние)
L = 3, ms: 1 1 1 0 -> 0 0 0 1
f1: 28 -1 3 5 -1 1 2 -1
f2: 3 20 -1 2 5 -1
f3: 16 -1
7 -> 7.1 -> 7 -> 7.2 -> 7 -> 8
f4: 3 16 20 28 -1
L = 2, ms: 1 0 0 0 -> 0 0 0 0
f1: 3 16 20 28 -1
f2: 28 -1 3 5 -1 1 2 -1
f3: 3 20 -1 2 5 -1
7 -> 7.2 -> 7 -> 8
f4: 2 3 5 5 -1
6. Если L = 0, то сортировка
завершена, результат в f[0].
7. Сливать отрезки из f[0], f[1],…, f[n-2]
в f[n-1] пока не исчерпается f[n-2]:
7.1. Пока все ms[i] > 0, все ms[i]--, а
ms[n-1]++
7.2. Сливать по одному отрезку из
каждого f[i], для которого ms[i] == 0
и уменьшать на 1 ms[i],
если ms[i] > 0.
8. L-- . Закрыть файлы f[n-2] и f[n-1].
Открыть f[n-2] на запись, f[n-1] на
чтение. Передвинуть указатели на
файлы и их имена, массивы ip и ms.
Перейти к 6.
40

41.

Пример 2 (слияние)
L = 1, ms: 0 0 0 0
f1: 2 3 5 5 -1
f2: 3 16 20 28 -1
f3: 28 -1 3 5 -1 1 2 -1
7 -> 7.2 -> 7 -> 8
f4: 1 2 2 3 3 5 5 16 20 28 -1
6. Если L = 0, то сортировка
завершена, результат в f[0].
7. Сливать отрезки из f[0], f[1],…, f[n-2]
в f[n-1] пока не исчерпается f[n-2]:
7.1. Пока все ms[i] > 0, все ms[i]--, а
ms[n-1]++
7.2. Сливать по одному отрезку из
каждого f[i], для которого ms[i] == 0
и уменьшать на 1 ms[i],
если ms[i] > 0.
8. L-- . Закрыть файлы f[n-2] и f[n-1].
Открыть f[n-2] на запись, f[n-1] на
чтение. Передвинуть указатели на
файлы и их имена, массивы ip и ms.
Перейти к 6.
41

42.

Ещё примеры (дома)
Не во всех файлах есть фиктивные отрезки:
6 85 69 95 44 20 75 7 46 27 96 42, n = 4 = 3 + 1
Во всех файлах есть фиктивные отрезки:
72 87 65 19 88 6 17 67 18 38 30, n = 4 = 3 + 1
40 35 94 15 59 20 14 71 26 88 39 10 83 34, n = 5 = 4 + 1
42