Similar presentations:
Комбинаторика. Правило произведения
1.
КоьбинаторикаПравило произведения
Если существует n вариантов выбора
первого элемента и для каждого из них имеется
m вариантов выбора второго элемента, то существует
n⋅m различных пар с выбранными первым и
вторым элементами.
2.
Правило произведения.Размещения с повторениями
3.
Соединения, содержащие n элементов, выбираемых изm различных видов, и отличающиеся одно от другого
либо составом, либо порядком следования в них
элементов называют размещениями с повторениями из
m по n.
Обозначение:
Читают: число размещений с повторениями
из эм по эн
4.
ПЕРЕСТАНОВКИ
Перестановками из n элементов называются
соединения, которые состоят из n элементов и
отличаются одно от другого только порядком
расположения
Обозначение:
5.
РАЗМЕЩЕНИЯ БЕЗ ПОВТОРЕНИЙЗадача 1. Сколько различных двухзначных чисел
можно записать с помощью цифр 1,2,3,4 при условии,
что в каждой записи нет одинаковых цифр?
12,13,14,
21,23,24
31,32,34,
41,42,43
По правилу произведения 4⋅3 = 12
Все соединения отличаются друг от друга
либо составом(12 и 24, либо порядком(12 и 12)
6.
Размещениями из m элементов по n элементов(n≤ m) называются такие соединения, каждое из
которых содержит n элементов, взятых из данных
m разных элементов, и которые отличаются одно от
другого либо самими элементами, либо порядком
их расположения.
Иногда такие размещения называют размещениями
без повторений.
Обозначение
7.
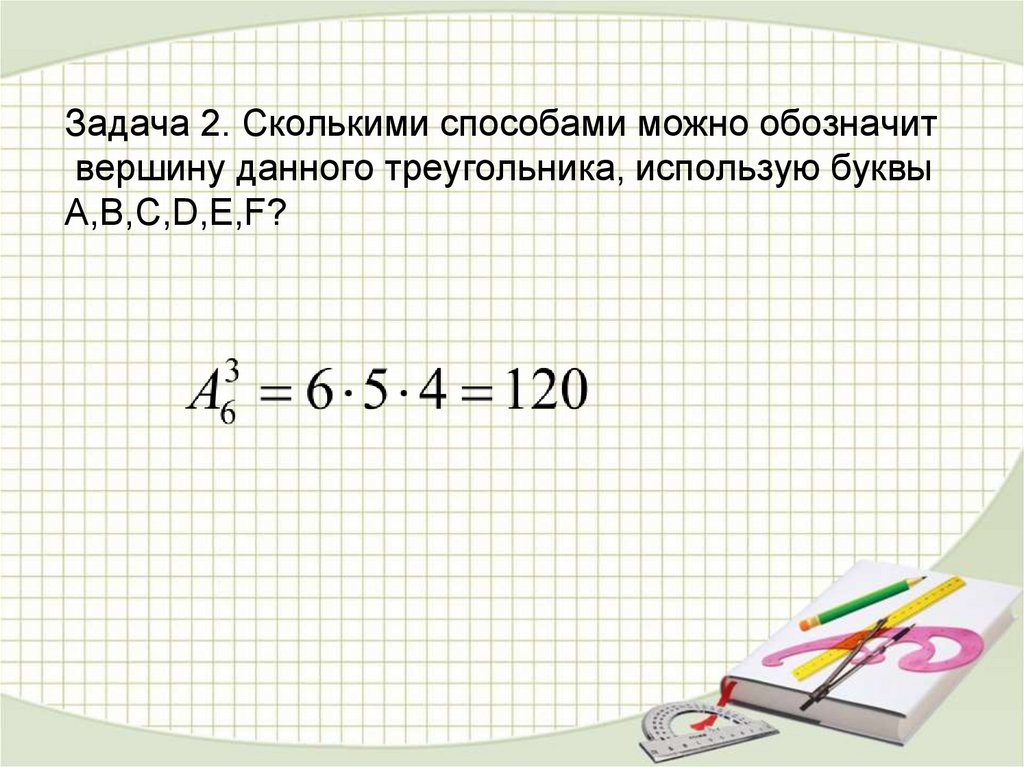
Задача 2. Сколькими способами можно обозначитвершину данного треугольника, использую буквы
А,В,С,D,E,F?
8.
Задача 3. Решить уравнение:Решение: n≥ 2 по формуле
Посторонний корень
9.
Задача 4. Вычислить10.
№ 31.Вычислите:РЕШЕНИЕ ЗАДАЧ
№ 32. В классе изучают 9 предметов. Сколькими способами можно
составить расписание на понедельник, если в этот день должно быт
6 разных предметов?
№ 33. Сколько существует способов для обозначения вершин
данного четырехугольника с помощью букв А,В,С,D,E,F?
№ 34. В классе 30 человек. Сколькими способами могут быть
выбраны из их состава староста и казначей?
№ 35. В чемпионате по футболу участвуют 10 команд. Сколько
существует различных возможностей занять командам первые три
места?
11.
№ 36. Найти значение выражения 1)2)
№ 37. Решите уравнение
12.
Сочетания без повторенийи бином Ньютона
13.
Задача 1: Из пяти шахматистов для участия в турнире нужновыбрать двоих. Сколькими способами это можно сделать?
Решение: Из пяти шахматистов модно составить
пар
Но из этих пар надо выбрать только те, которые различаются лишь
составом участников, таких пар в 2 раза меньше, т.е.
При решении этой задачи из 5 человек были образованы пары –
соединения по 2 человека, которые отличались друг от друга только
составом.
Такие соединения называют сочетаниями.
14.
Сочетаниями из m элементов по n в каждом ( n≤ m) называютсятакие соединения, каждое из которых содержит n элементов, взятых
из данных m элементов, и которые отличаются одно от другого по
крайней мере одним элементом. Иногда такие сочетания называют
сочетаниями без повторений.
При решении первой задачи было установлено
15.
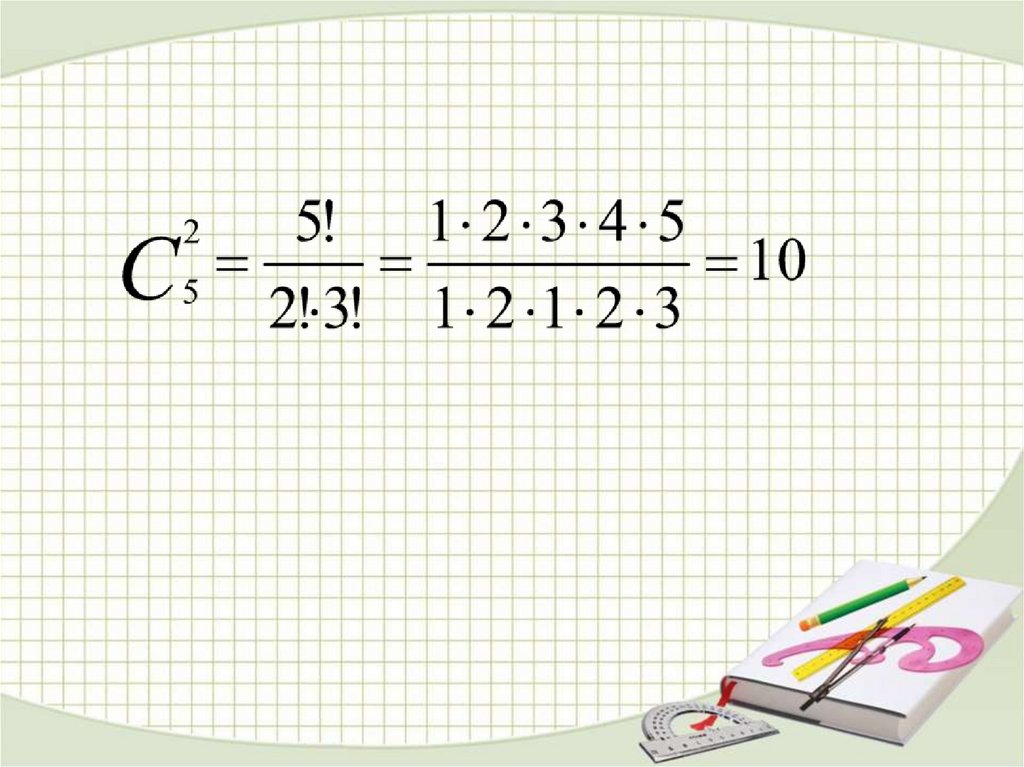
Например16.
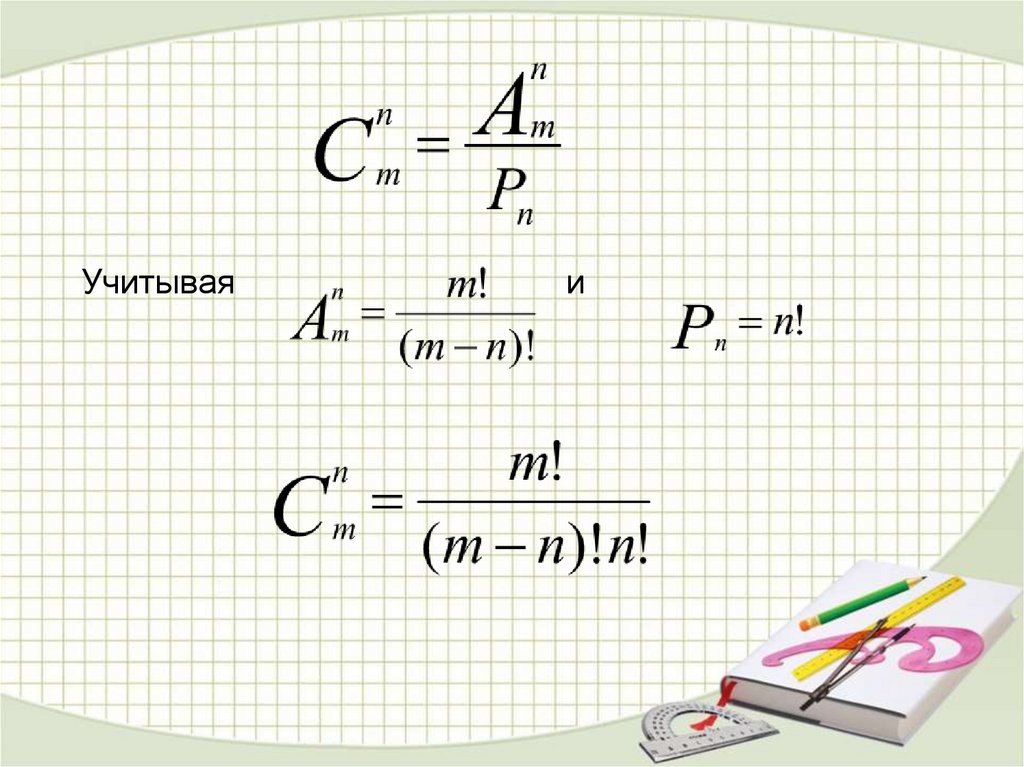
Учитываяи
17.
18.
Задача 2:Сколько существует способов выбора трёх карт из колодыв 36 карт?
Решение: Изъятые из колоды 3 карты без учета порядка их
расположения в наборе являются сочетаниями из 36 по 3.
19.
СВОЙСТВА СОЧЕТАНИЙ20.
БИНОМ НЬЮТОНАЗадача 3: Записать разложение бинома (2х-1/2)5 .
21.
ЛитератураАлгебра и начала математического анализа 11 класс,
Колягин Ю.М., Ткачев М.В., Федорова Н.Е., Шабунин М.И.,
М. : «Просвещение», 2011


















 mathematics
mathematics








