Правильные многогранники

1.

ПРАВИЛЬНЫЕ
МНОГОГРАННИКИ

2.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Правильный многогранник, или Платоново тело —
это выпуклый многогранник с максимально
возможной симметрией.
Многогранник называется правильным, если:
1. он выпуклый
2. все его грани являются равными правильными
многоугольниками
3. в каждой его вершине сходится одинаковое
число граней
4.
все его двугранные углы равны

3.

СОСТАВЛЕН ИЗ ЧЕТЫРЁХ РАВНОСТОРОННИХ
ТРЕУГОЛЬНИКОВ. КАЖДАЯ ЕГО ВЕРШИНА
ЯВЛЯЕТСЯ ВЕРШИНОЙ ТРЁХ
ТРЕУГОЛЬНИКОВ. СЛЕДОВАТЕЛЬНО, СУММА
ПЛОСКИХ УГЛОВ ПРИ КАЖДОЙ ВЕРШИНЕ
РАВНА 180º.

4.

СОСТАВЛЕН ИЗ ШЕСТИ КВАДРАТОВ. КАЖДАЯ
ВЕРШИНА КУБА ЯВЛЯЕТСЯ ВЕРШИНОЙ ТРЁХ
КВАДРАТОВ. СЛЕДОВАТЕЛЬНО, СУММА
ПЛОСКИХ УГЛОВ ПРИ КАЖДОЙ ВЕРШИНЕ
РАВНА 270º.

5.

СОСТАВЛЕН ИЗ ВОСЬМИ РАВНОСТОРОННИХ
ТРЕУГОЛЬНИКОВ. КАЖДАЯ ВЕРШИНА
ОКТАЭДРА ЯВЛЯЕТСЯ ВЕРШИНОЙ ЧЕТЫРЁХ
ТРЕУГОЛЬНИКОВ. СЛЕДОВАТЕЛЬНО, СУММА
ПЛОСКИХ УГЛОВ ПРИ КАЖДОЙ ВЕРШИНЕ 240º.

6.

СОСТАВЛЕН ИЗ ДВЕНАДЦАТИ ПРАВИЛЬНЫХ
ПЯТИУГОЛЬНИКОВ. КАЖДАЯ ВЕРШИНА
ДОДЕКАЭДРА ЯВЛЯЕТСЯ ВЕРШИНОЙ ТРЁХ
ПРАВИЛЬНЫХ ПЯТИУГОЛЬНИКОВ.
СЛЕДОВАТЕЛЬНО, СУММА ПЛОСКИХ УГЛОВ ПРИ
КАЖДОЙ ВЕРШИНЕ РАВНА 324º.

7.

СОСТАВЛЕН ИЗ ДВАДЦАТИ РАВНОСТОРОННИХ
ТРЕУГОЛЬНИКОВ. КАЖДАЯ ВЕРШИНА
ИКОСАЭДРА ЯВЛЯЕТСЯ ВЕРШИНОЙ ПЯТИ
ТРЕУГОЛЬНИКОВ. СЛЕДОВАТЕЛЬНО, СУММА
ПЛОСКИХ УГЛОВ ПРИ КАЖДОЙ ВЕРШИНЕ РАВНА
300º.

8.

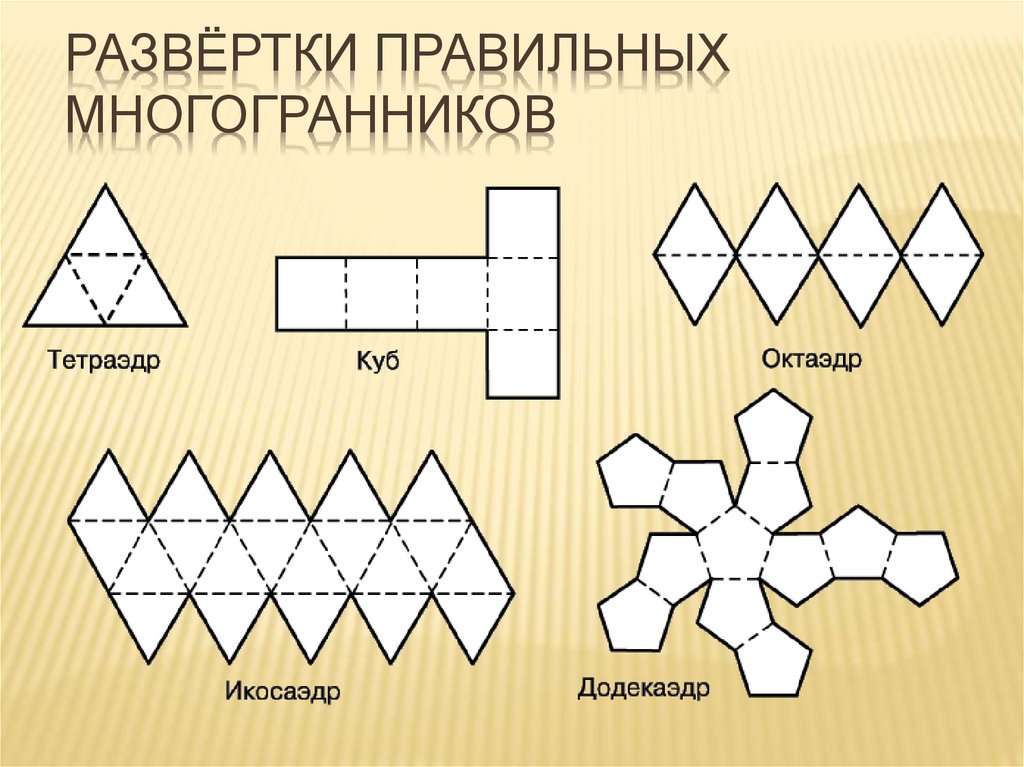
РАЗВЁРТКИ ПРАВИЛЬНЫХ
МНОГОГРАННИКОВ

9.

НАЗВАНИЯ МНОГОГРАННИКОВ
пришли из Древней Греции,
в них указывается число граней:
«эдра» грань;
«тетра» 4;
«гекса» 6;
«окта» 8;
«икоса» 20;
«додека» 12.

10.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
ИЛИ ПЛАТОНОВЫ ТЕЛА
Дата рождения: 428 до н. э.
Место рождения:
Афины
Дата смерти: 347 год до н. э.
Основные интересы:
Метафизика, этика, эстетика,
политика, образование,
философия математики

11.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
В КАРТИНЕ МИРА ПЛАТОНА
Платон считал, что мир строится из четырёх «стихий» –
огня, земли, воздуха и воды, а атомы этих «стихий»
имеют форму четырёх правильных многогранников.
Тетраэдр олицетворял огонь, поскольку его вершина
устремлена вверх, как у разгоревшегося пламени.
Икосаэдр – как самый обтекаемый – воду.
Куб – самая устойчивая из фигур – землю.
Октаэдр – воздух.
В наше время эту систему можно сравнить с четырьмя
состояниями вещества – твёрдым, жидким, газообразным
и пламенным.
Пятый многогранник – додекаэдр символизировал весь
мир и почитался главнейшим.

12.

ТЕТРАЭДР - ОГОНЬ

13.

КУБ - ЗЕМЛЯ

14.

ОКТАЭДР - ВОЗДУХ

15.

ИКОСАЭДР - ВОДА

16.

ДОДЕКАЭДР - ВСЕЛЕННАЯ

17.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ И
“ТАЙНЫ МИРОЗДАНИЯ” И.КЕПЛЕРА.
Дата рождения:
27.12.1571
Место рождения:
Вайль-дер-Штадт,
Священная Римская империя
Научная сфера:
астрономия, математика,
физика
Известен как автор Законов
движения планет

18.

«КОСМИЧЕСКИЙ КУБОК» КЕПЛЕРА
Кеплер предположил: есть связь между пятью
правильными многогранниками и шестью известными
планетами Солнечной системы.
Это значит, что в сферу орбиты Сатурна можно
вписать куб, в который вписывается сфера орбиты
Юпитера. В неё, в свою очередь, вписывается тетраэдр,
описанный около сферы орбиты Марса. В сферу орбиты
Марса вписывается додекаэдр, к который вписывается
сфера орбиты Земли. А она описана около икосаэдра, в
который вписана сфера орбиты Венеры. Сфера этой
планеты описана около октаэдра, в который
вписывается сфера Меркурия
Модель Солнечной
системы И. Кеплера
Эта модель Солнечной системы получила название
«Космического кубка» Кеплера. Год за годом учёный
уточнял свои наблюдения, перепроверял данные коллег,
но, наконец, нашёл в себе силы отказаться от
заманчивой гипотезы. Однако её следы
просматриваются в третьем законе Кеплера, где
говориться о кубах средних расстояний от Солнца.

19.

МНОГОГРАННИКИ В ГЕОЛОГИИ
Гипотеза В.Макарова и В.Морозова:
Ядро Земли имеет форму и свойства растущего кристалла,
оказывающего воздействие на развитие всех природных процессов,
идущих на планете,
Лучи кристалла обуславливают икосаэдро-додекаэрическую структуру
Земли.
Многие залежи полезных ископаемых тянутся вдоль икосаэдрододекаэдровой сетки.
В местах пересечения рёбер располагаются очаги древних культур и
цивилизаций.
В этих точках наблюдаются максимумы и минимумы атмосферного
давления, гигантские завихрения Мирового океана,
шотландское озеро Лох-Несс, Бермудский треугольник,

20.

КРАСОТА ФОРМ В ПРИРОДЕ
“Природа вскармливает
на своём лоне
неисчерпаемое
количество
удивительных созданий,
которые по красоте и
разнообразию далеко
превосходят все
созданные искусством
человека формы”
Э. Геккель.

21.

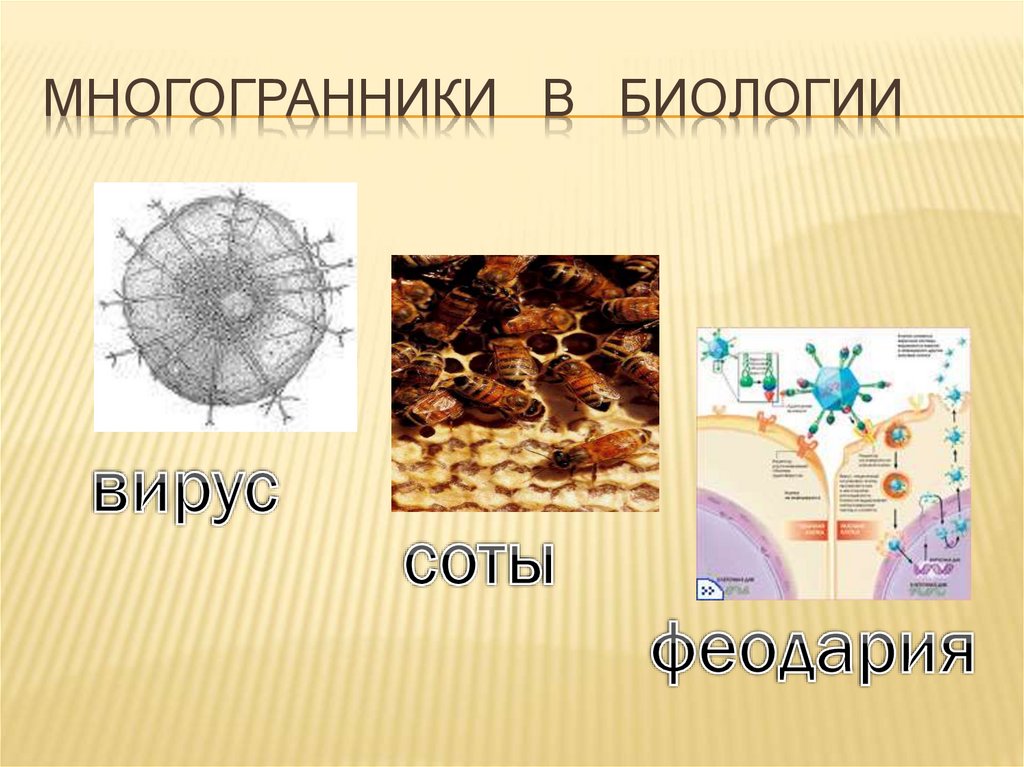
МНОГОГРАННИКИ В БИОЛОГИИ

22.

МНОГОГРАННИКИ И КРИСТАЛЛЫ
В кристаллографии
существует раздел,
который называется
«геометрическая
кристаллография»

23.

МНОГОГРАННИКИ В ХИМИИ

24.

МНОГОГРАННИКИ В ХИМИИ

25.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
В ИСКУССТВЕ.
В эпоху Возрождения большой
интерес к формам правильных
многогранников проявили
скульпторы, архитекторы,
художники. Леонардо да Винчи
увлекался теорией
многогранников и часто
изображал их на своих
полотнах. Он проиллюстрировал
изображениями правильных и
полуправильных
многогранников книгу своего
друга монаха Луки Пачоли "О
божественной пропорции".

26.

Иллюстрация
Леонардо да Винчи к книге
«О божественной пропорции»
Изобретение
Леонардо да Винчи
(парашют)

27.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
В ИСКУССТВЕ.
Другим знаменитым
художником эпохи
Возрождения, также
увлекавшимся геометрией,
был Альбрехт Дюрер.
В его известной гравюре
"Меланхолия" изображен
додекаэдр. В 1525 году
Дюрер написал трактат, в
котором представил пять
правильных многогранников,
поверхности которых служат
хорошими моделями
перспективы.

28.

Альбрехт Дюрер
"Меланхолия"

29.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
В ИСКУССТВЕ.
Сальвадор Дали на
картине «Тайная вечеря»
изобразил
И. Христа со своими
учениками на фоне
огромного прозрачного
додекаэдра.

30.

«Тайная Вечеря» Сальвадор Дали

31.

МНОГОГРАННИКИ В АРХИТЕКТУРЕ

32.

33.

МОДА И МНОГОГРАННИКИ

34.

КАК МНОГО СУЩЕСТВУЕТ ПРАВИЛЬНЫХ
МНОГОГРАННИКОВ?
Учёными достаточно хорошо изучены
правильные многогранники.
Доказано, что существует пять видов таких
многогранников.
Не существует правильного многогранника,
гранями которого являются правильные
шестиугольники, семиугольники и, вообще, nугольники при n≥6.
Сам ли человек их придумал?
Скорее всего – нет, он подсмотрел их у природы.

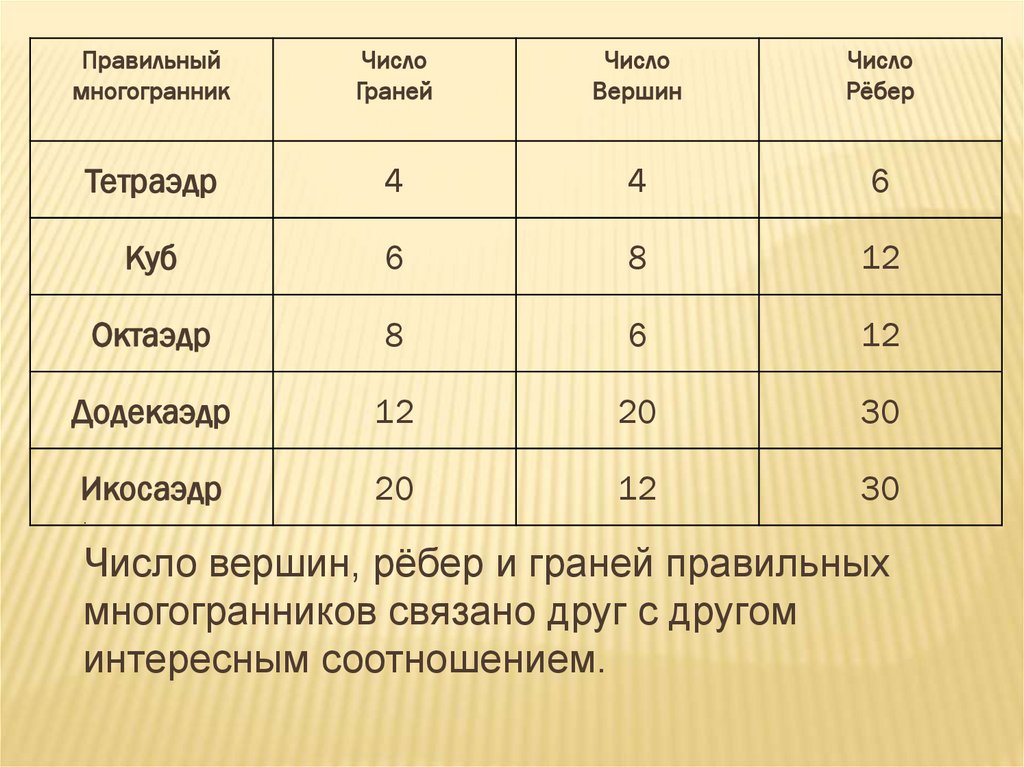
35.

Правильный
многогранник
Число
Граней
Число
Вершин
Число
Рёбер
Тетраэдр
4
4
6
Куб
6
8
12
Октаэдр
8
6
12
Додекаэдр
12
20
30
Икосаэдр
20
12
30
.
Число вершин, рёбер и граней правильных
многогранников связано друг с другом
интересным соотношением.

36.

ФОРМУЛА ЭЙЛЕРА
Сумма числа граней и вершин любого
многогранника
равна числу рёбер, увеличенному на 2.
Г+В=Р+2
Число граней плюс число вершин
минус число рёбер
в любом многограннике равно 2.
Г+В Р=2

37.

Л.Эйлер
(1707-1783)
Один из величайших
математиков мира,
работы которого
оказали решающее
влияние на развитие
многих современных
разделов математики.

38.

Правильных многогранников
вызывающе мало, но этот
весьма скромный по
численности отряд сумел
пробраться в самые глубины
различных наук.
Л. Кэрролл