Similar presentations:
Свойства криптографических преобразований
1. Свойства криптографических преобразований
2. Криптографическая стойкость
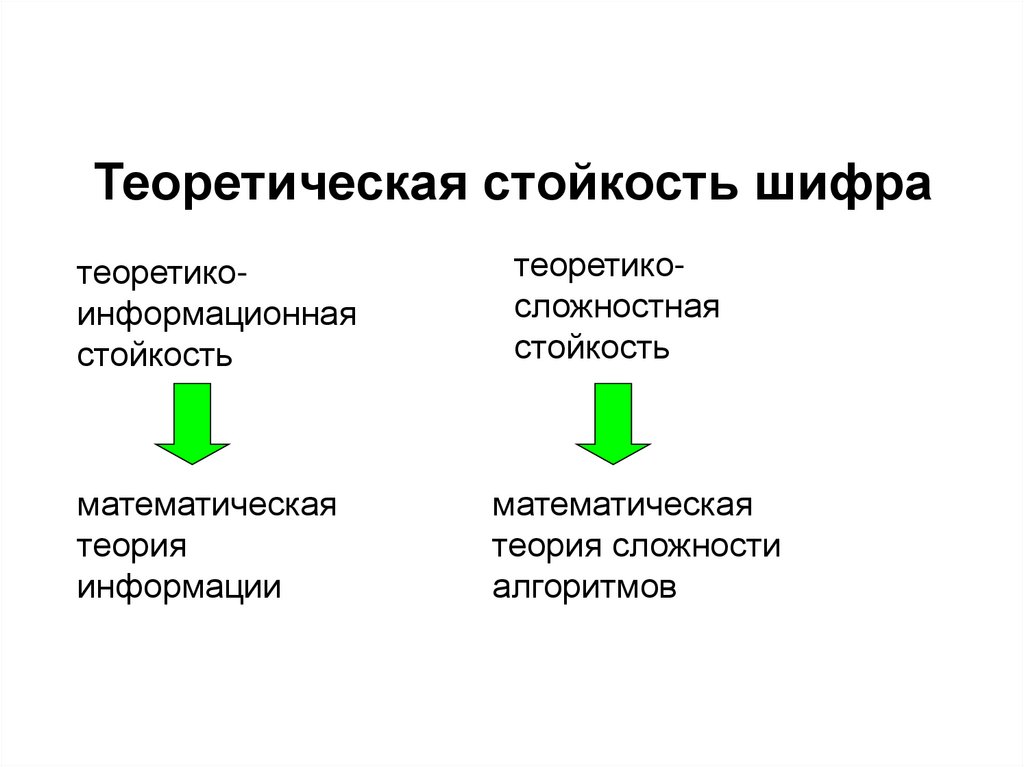
3. Теоретическая стойкость шифра
теоретикоинформационнаястойкость
теоретикосложностная
стойкость
математическая
теория
информации
математическая
теория сложности
алгоритмов
4. Теоретико-информационная стойкость
P x P y | xP x | y
P y
P y P k P x Dk y
k
P y | x P k
i
x Dk y
5.
Абсолютно стойкий (совершенный) шифрP x P y | x
P x | y
P y
P x | y P x
P y | x P y
1
P y | x
K
6.
add X , Y , K , E, DX , Y , K 3
Ek x x k mod 3
Dk y y k mod 3
7.
Px(xi) – вероятность появления открытого текста xi;Py(yi) – вероятность появления шифртекста yi;
Pk(ki) – вероятность появления ключа ki;
Px|y(xi|yi) – условная вероятность появления
открытого текста xi при появлении шифртекста yi;
Py|x(yi|xi) – условная вероятность появления
шифртекста yi при появлении открытого текста xi.
1
Pk ki Pk
K
P x 1
x
i
i
8.
P x P y | xP x | y
P y
1
P y P k
K
Вероятности появления шифртекстов P(y):
P y P k P x Dk y
k
Py 0 P 0 P 0 P 1 P 2 P 2 P 1 P P x P
2
x
k
x
k
x
k
k
x
i 0
2
i
k
Py 1 P 0 P 1 P 1 P 0 P 2 P 2 P P x P
x
k
x
k
x
k
k
i 0
x
i
k
Py 2 P 0 P 2 P 1 P 1 P 2 P 0 P P x P
2
x
k
x
k
x
k
k
i 0
x
i
k
9.
Условная вероятность P(y|x) появления ШТ для заданных ОТP y | x P k x Dk y
i
Py|x| x 0 | 0 Pk 0
Py|x 0 | 0 Pk 0
Py|x 1 | 0 Pk 1 Py|x 2 | 0 Pk 2
Py|x 0 | 1 Pk 2
Py|x 1 | 1 Pk 0 Py|x 2 | 1 Pk 1
Py|x 0 | 2 Pk 1
Py|x 1 | 2 Pk 2 Py|x 2 | 2 Pk 0
1
P y | x P k
K
10.
add X , Y , K , E, D1
P y P k
K
X , Y , K 3
Ek x x k mod 3
Dk y y k mod 3
1
P y | x P k
K
P x P y | x P x P k
P x | y
P x
P y
P k
шифр является абсолютно стойким
11.
mul X , Y , K , E, DX , Y 3
K 3
Ek x x k mod 3 Dk y y k
1
mod 3
1 1
Pk ki Pk
K 2
1 1
Px xi
X 3
12.
Вероятности появления шифртекстов P(y):P y P k P x Dk y
k
1
Py 0 Px 0 Pk 1 Px 0 Pk 2 2 Pk Px
3
1
Py 1 Px 1 Pk 1 Px 2 Pk 2 2 Pk Px
3
1
Py 2 Px 2 Pk 1 Px 1 Pk 2 2 Pk Px
3
1
P y P x
3
13.
Условная вероятность P(y|x) появления ШТ для заданных ОТ,
,
P y | x P k x Dk y
i
Py|x 0 | 0 Pk 1 Pk 2 2 Pk 1
Py|x 0 | 1 0
Py|x 0 | 2 0
Py|x 1 | 0 0
Py|x 2 | 0 0
1
Py|x 1 | 1 Pk 1
2
1
Py|x 1 | 2 Pk 2
2
1
Py|x 2 | 1 Pk 2
2
1
Py|x 2 | 2 Pk 1
2
14.
Условная вероятность P(x|y)1
Px 0 Py|x 0 | 0 3 1
Px| y 0 | 0
1
1
Py 0
3
шифр не является абсолютно стойким
Px| y 0 | 1
Px| y 0 | 2
Px 0 Py| x 1 | 0
Py 1
0
Px 0 Py|x 2 | 0
Py 2
0
15. Свойство абсолютно стойкого шифра
K Y Xadd: |K|=|Y|=|X|=3
mul : |K|=2, |K| < |Y| и |K| < |X|
16. Теорема об абсолютно стойком шифре
: |K|=|Y|=|X|x X , y Y
k K : Ek x y
1
p k
, k K
K
17.
для абсолютно стойкого шифра количество возможных ключей должнопревосходить количество возможных шифртекстов
4 11 31 32 0 1 17 14 11 30 18 13 14 32 17 18 14 9 10 14 3 14 32 24 8 20 16 0 32 10 14 11 8 23 5 17 18 2
14 32 2 14 7 12 14 6 13 27 21 32 10 11 30 23 5 9 32 4 14 11 6 13 14 32 15 16 5 2 14 17 21 14 4 8 18 28
32 10 14 11 8 23 5 17 18 2 14 32 2 14 7 12 14 6 13 27 21 32 24 8 20 16 18 5 10 17 18 14 2
11 11 16 31 12 30 4 21 31 25 22 4 31 15 2 15 11 7 18 1 23 29 4 10 24 9 31 1 24 22 28 16 30 14 17 12 11
10 29 4 28 22 23 23 10 14 16 15 25 18 17 23 6 6 24 27 12 15 30 24 8 18 8 32 33 4 15 17 14 17 28 16 4
29 15 7 16 27 4 6 13 19 14 7 1 1 1 8 21 10 13 29 11 23 11 22 19 1 21 10 31 27 10 18 2 1 30 32 10
15 22 14 30 12 31 21 2 9 22 7 17 12 14 19 0 25 16 28 15 26 10 3 1 32 29 14 1 23 32 9 27 5 4 22 29 29
12 10 3 30 3 30 2 24 20 29 9 13 17 27 1 3 29 29 3 11 19 11 2 14 31 22 31 15 20 20 19 28 1 16 30 8 4 0 2
15 4 18 17 21 9 19 24 19 3 15 7 23 24 20 8 25 29 24 16 7 0 12 18 18 10 28 23 12 18 15 13 12
11 11 16 31 12 30 4 21 31 25 22 4 31 15 2 15 11 7 18 1 23 29 4 10 24 9 31 1 24 22 28 16 30 14 17 12 11
10 29 4 28 22 23 23 10 14 16 15 25 18 17 23 6 6 24 27 12 6 6 3 10 17 11 25 2 6 21 4 12 29 14 3 17 4 15
7 16 27 4 6 13 19 14 7 1 1 1 8 21 10 13 29 11 23 11 22 19 1 21 10 31 27 10 18 2 1 30 32 10
4 11 31 32 0 1 17 14 11 30 18 13 14 32 17 18 14 9 10 14 3 14 32 24 8 20 16 0 32 10 14 11 8 23 5 17 18 2
14 32 2 14 7 12 14 6 13 27 21 32 10 11 30 23 5 9 32 13 5 32 4 14 11 6 13 14 32 15 16 5 2 27 24 0 18 28
32 10 14 11 8 23 5 17 18 2 14 32 2 14 7 12 14 6 13 27 21 32 24 8 20 16 18 5 10 17 18 14 2
для абсолютно стойкого шифра количество возможных ключей не должно
превышать количество возможных шифртекстов
18. Энтропийный подход
H X | Y H Xadd : H X | Y Py 0 H X Py 1 H X Py 2 H X
1
n H X H X
n
mul : H X | Y Py 0 H X | 0 Py 1 H X | 1 Py 2 H X | 2
Py 1 Py 2 0,667 H X
19. Теоретико-сложностная стойкость шифра. Практическая стойкость шифра.
20. Обозначения
– вычислительный алгоритмx – входные данные алгоритма;
T (x) – время выполнения алгоритма на данных x;
S (x) – память, требуемая для выполнения алгоритма
на данных x;
Tφ – временная сложность алгоритма;
Sφ – пространственная (емкостная) сложность
алгоритма;
– вероятность успешного завершения алгоритма
21.
Алгоритмоднородный
неоднородный
0x1F + 0x02
0x1F • 0x02
0x1F + 0x1F
0x1F • 0x1F
22.
Временная сложность в наихудшем случаеT max T x
x
Временная сложность в наилучшем случае
T min T x
x
Временная сложность в среднем
T M x T x
23.
Пространственная сложность в наихудшем случаеS max S x
x
Пространственная сложность в наилучшем случае
S min S x
x
Пространственная сложность в среднем
S M x S x
Вероятность успешного завершения
24. Возможности противника
T0 – допустимая сложность проведения атакиS0 – объем памяти
0 – допустимая вероятность успешного
проведения атаки
T0 = N t
25. Практическая стойкость
Опасный алгоритмT T0
S S 0
0
Шифр практически стойкий
T T0
S S 0
0


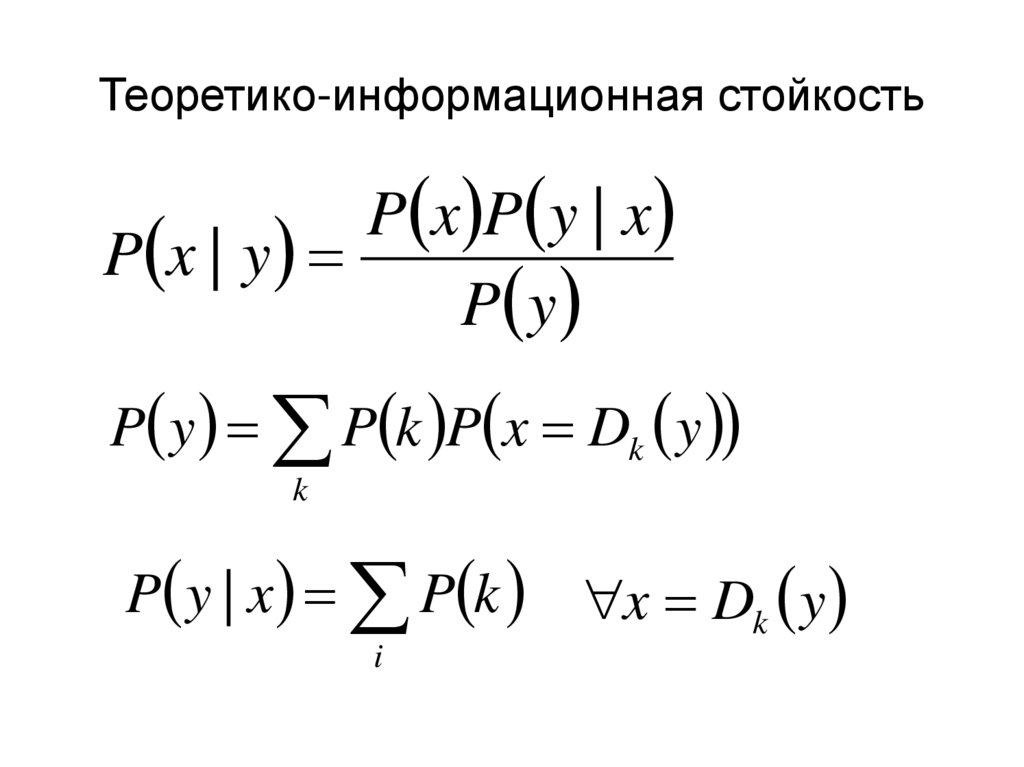

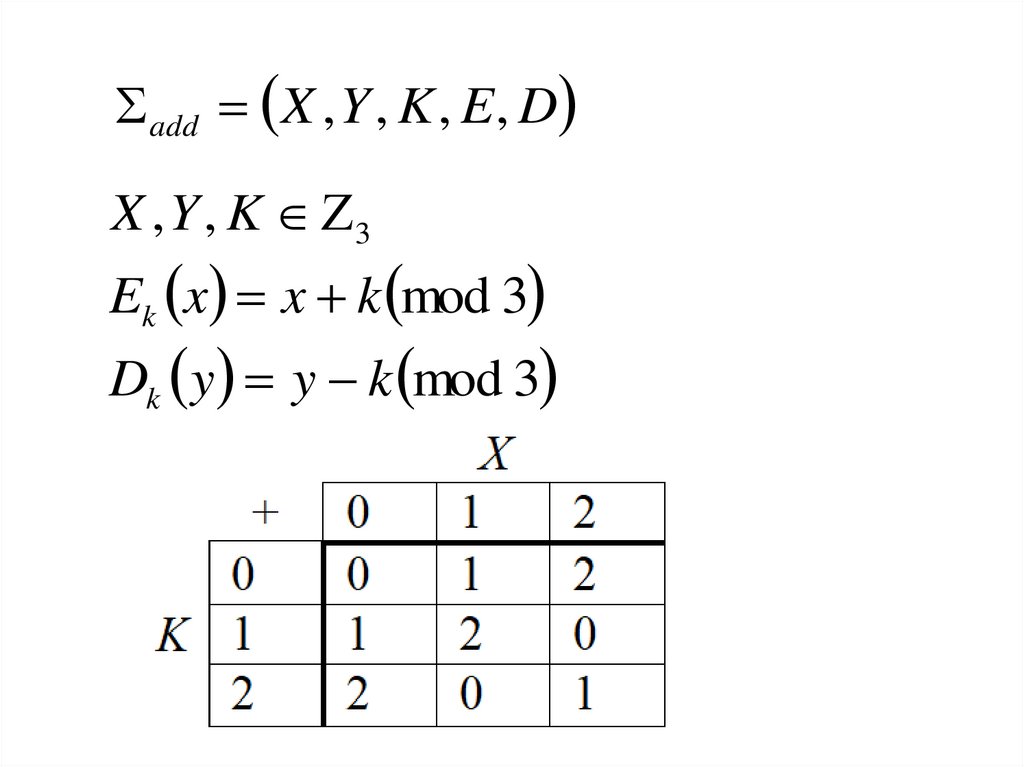



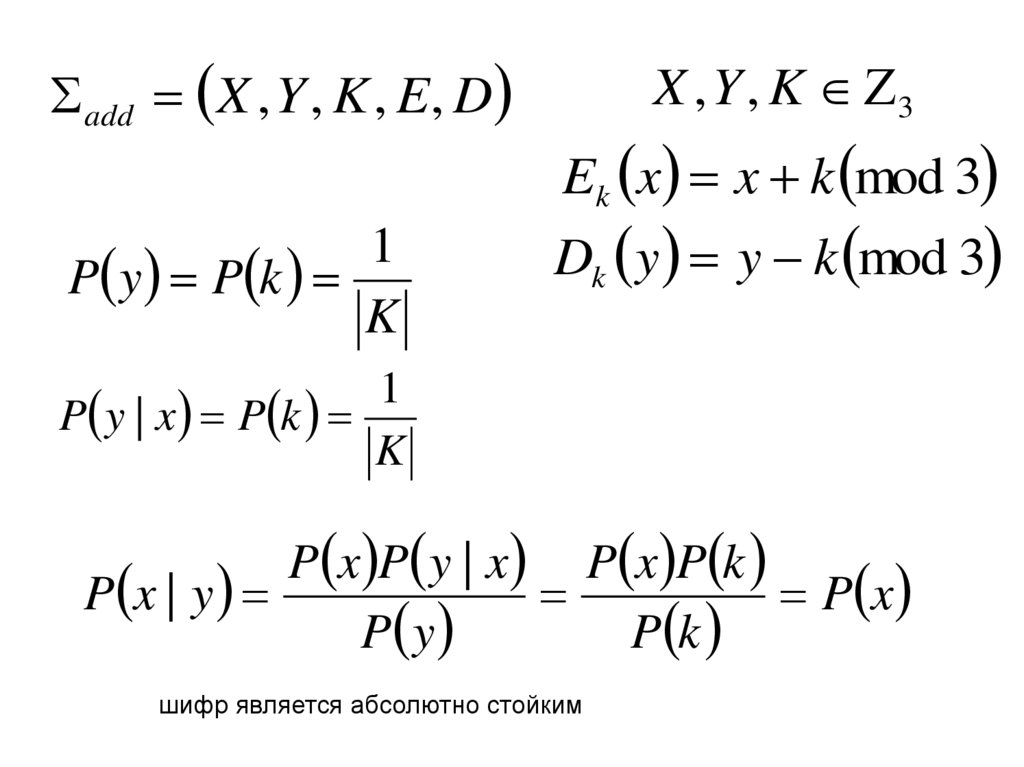
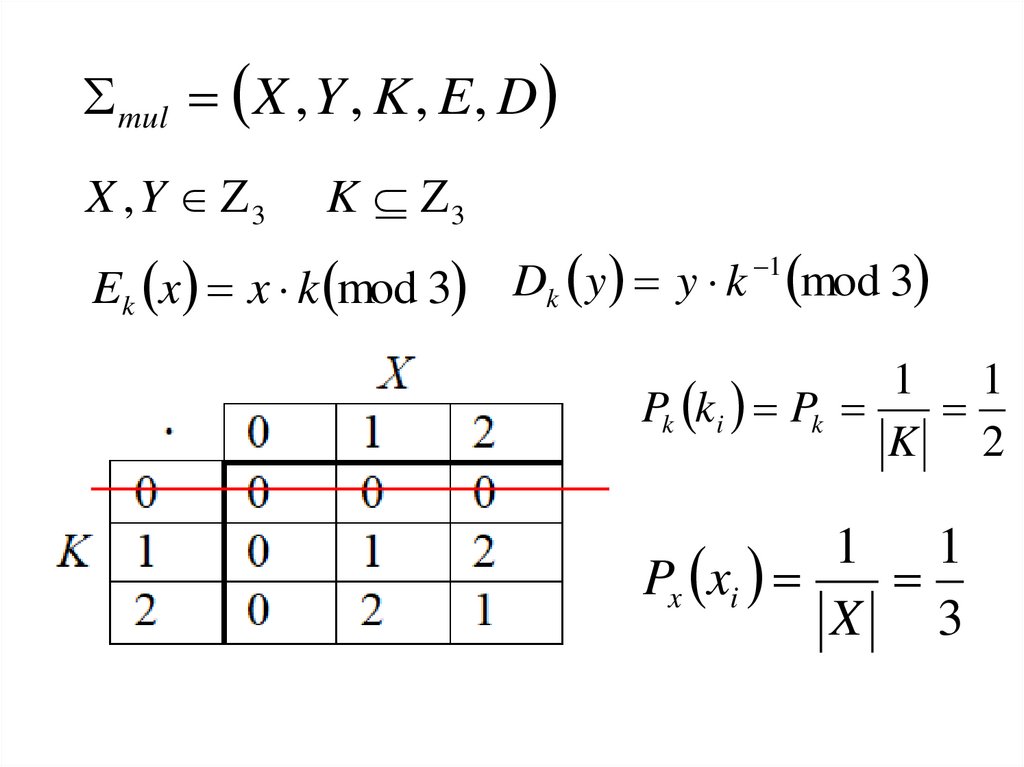






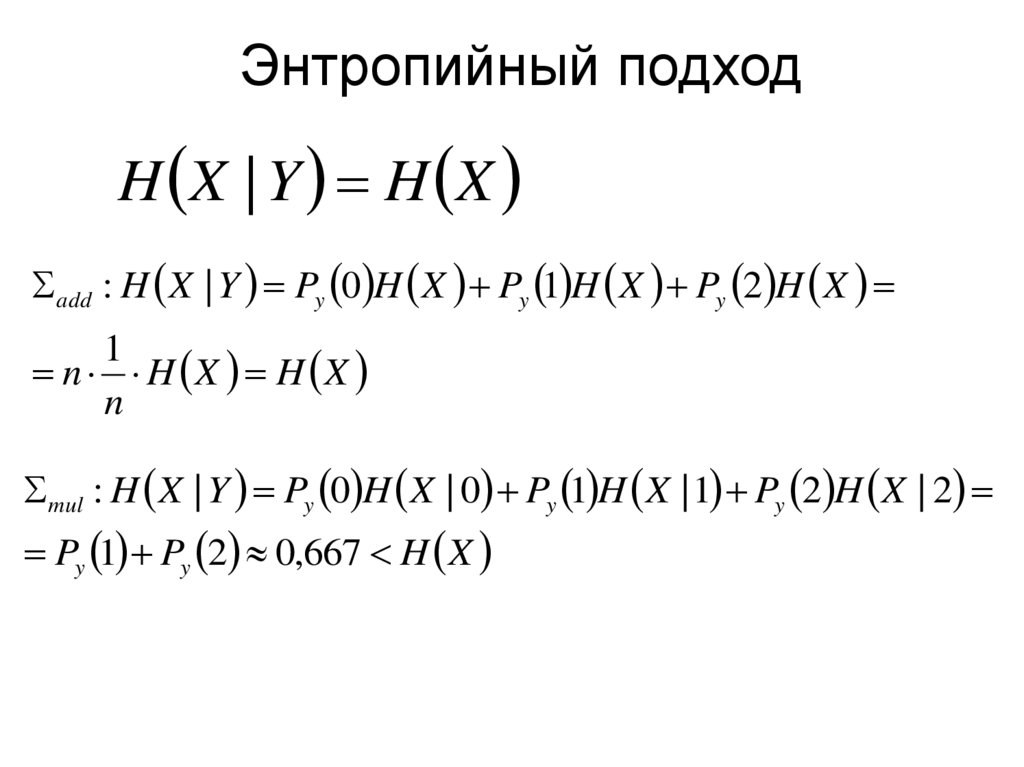







 informatics
informatics