Множества

1.

Выполнил:
Студент группы С-215
Маёнов К.А.

2.

• Георг Кантор (1845-1918)
• Профессор математики и
философии, основоположник
современной теории множеств.
• «Под множеством мы
подразумеваем объединение в
целое определённых,
различающихся между собой
объектов нашего представления
или мышления». Георг Кантор

3.

Основное понятие в математике - понятие
множества.
Понятие множество относится к первоначальным
понятиям, не подлежащим определению.
Под множеством подразумевается некоторая
совокупность однородных объектов.
Предметы ( объекты), составляющие множество,
называются элементами.

4.

Множества обозначаются заглавными буквами латинского
алфавита: A, B, C, X и др.
Элементы множества обозначаются строчными буквами
латинского алфавита : a, b, c, d и др.
Запись M = { a , b, c, d } означает, что множество М состоит
из элементов a , b, c, d.
Є – знак принадлежности. Запись а є М обозначает, что
объект а является элементом множества М и читается так:
« а принадлежит множеству М »

5.

Численность множества- число элементов в данном множестве.
Обозначается так : n
Записывается так : n (М) = 4
Множества бывают:
Конечные множества- состоят из конечного числа элементов, когда
можно пересчитать все элементы множества.
Бесконечные множества- когда невозможно пересчитать все
элементы множества.
Пустые множества- множества, не содержащие элементов и
обозначают так: Ø . Записывают так: n (A)=0 ; A= Ø
Пустое множество является подмножеством любого множества.

6.

Дискретные множества(прерывные)- имеют отдельные элементы. Путём
счёта распознаются.
Непрерывные множества- нет отдельных элементов. Распознаются путём
измерения.
Конечные множества- состоят из конечного числа элементов, когда можно
пересчитать все элементы множества.
Бесконечные множества- когда невозможно пересчитать все элементы
множества.
Упорядочные множества. Элемент из множества предшествует или
следует за другим. Множество натуральных чисел, расположенных в виде
натурального ряда.
Неупорядочные множества. Любое неупорядочное множество можно
упорядочить.

7.

Перечислением элементов (подходит для конечных множеств).
Указать характеристическое свойство множества, т.е. то свойство,
которым обладают все элементы данного множества.
С помощью изображения :
- На луче
- В виде графика
С помощью кругов Эйлера. В основном используется при выполнении
действий с множествами или демонстрации их отношений.

8.

Если любой элемент множества
В принадлежит множеству А,
то множество В называется
подмножеством множества А.
- Знак включения.
Запись В
А означает,
что множество В является
подмножеством множества А.

9.

Собственное подмножество. Множество В называется
собственным подмножеством множества А, если
выполняются условия: В≠Ø, В≠А.
Не собственные подмножества. Множество В называется
не собственным подмножеством множества А, если
выполняются условия: В≠Ø, В=А.
Пустое множество является подмножеством любого
множества.
Любое множество является подмножеством самого себя.

10.

Множества равны, если они состоят из одних и тех же элементов.
Два множества являются равными , если каждый из них является
подмножеством другого.
В этом случае пишут: А=В
А=В
А
В

11.

Пересечение множеств.
Объединение множеств.
Разность множеств.
Дополнение множества.

12.

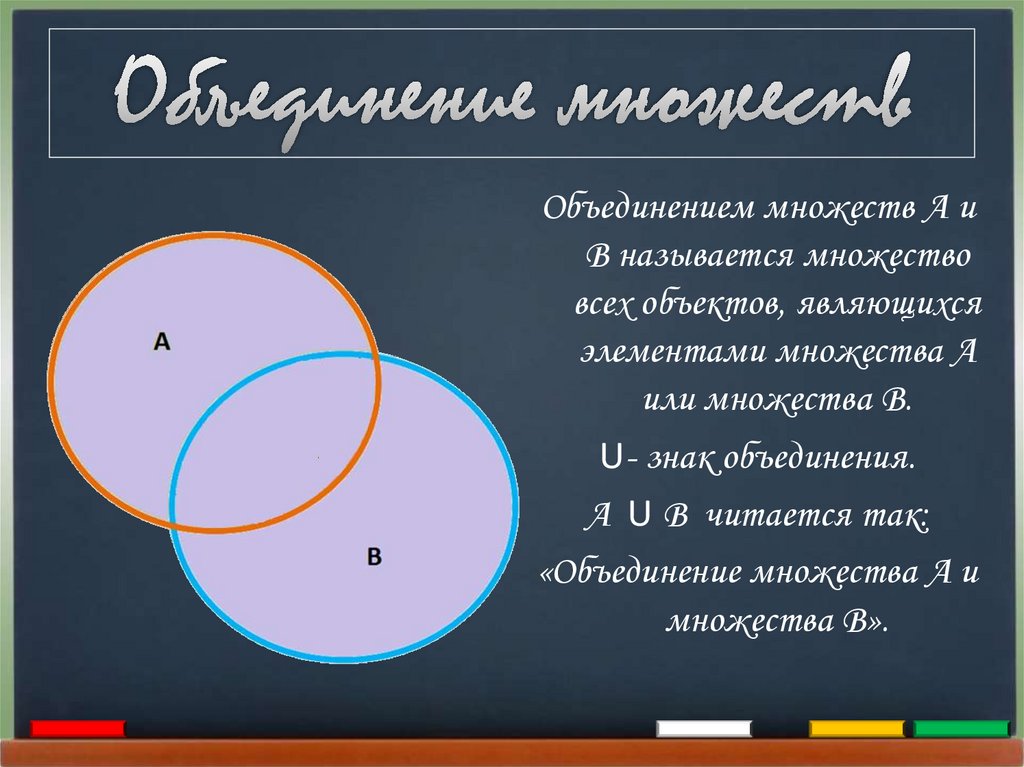
Объединением множеств А и
В называется множество
всех объектов, являющихся
элементами множества А
или множества В.
U- знак объединения.
А U В читается так:
«Объединение множества А и
множества В».

13.

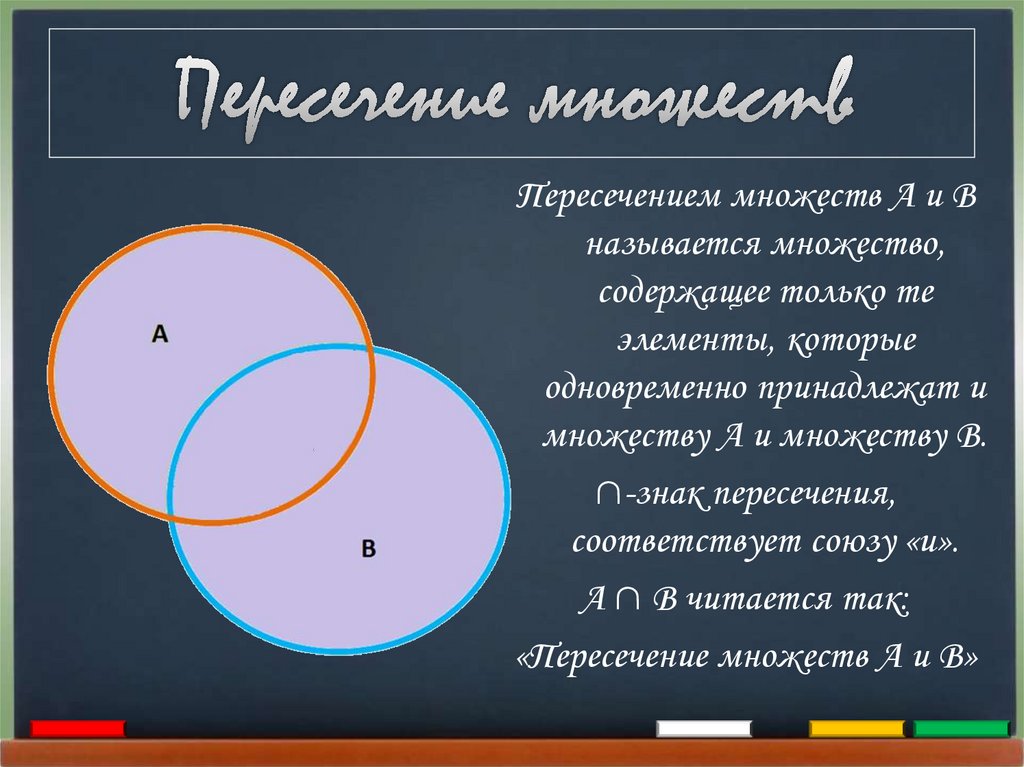
Пересечением множеств А и В
называется множество,
содержащее только те
элементы, которые
одновременно принадлежат и
множеству А и множеству В.
∩-знак пересечения,
соответствует союзу «и».
А ∩ В читается так:
«Пересечение множеств А и В»

14.

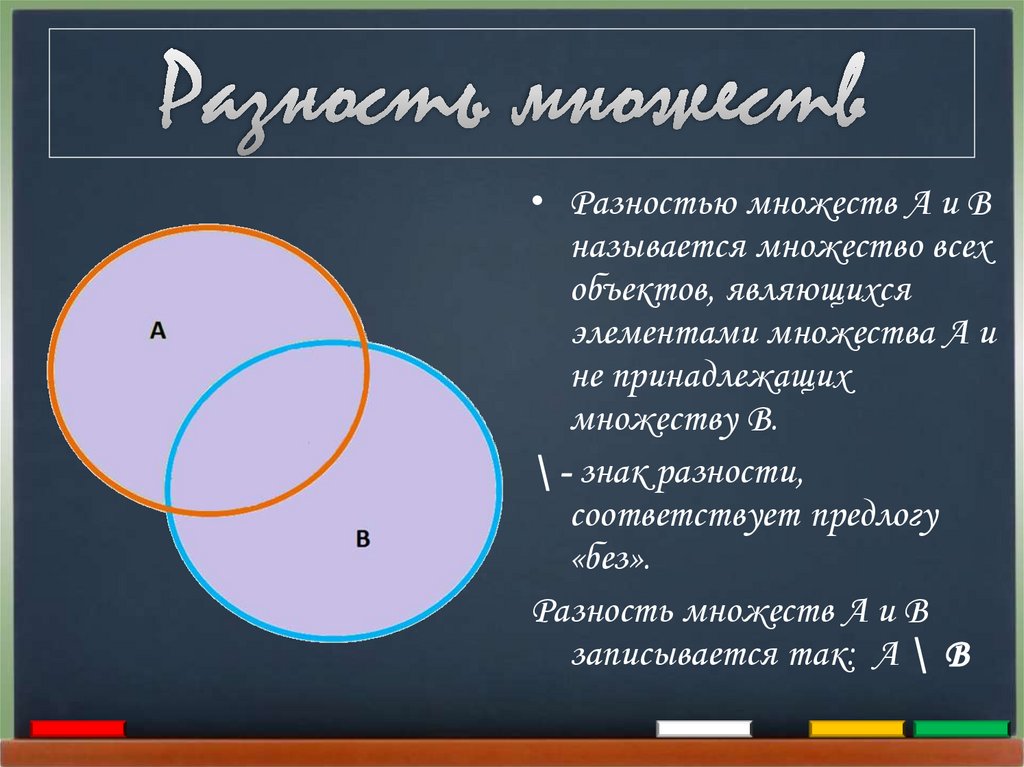
• Разностью множеств А и В
называется множество всех
объектов, являющихся
элементами множества А и
не принадлежащих
множеству В.
\ - знак разности,
соответствует предлогу
«без».
Разность множеств А и В
записывается так: А \ В

15.

• Множество элементов
множества В, не
принадлежащих множеству А,
называется дополнением
множества А до множества В.
Часто множества являются
подмножествами некоторого
основного, или универсального
множества U.
Дополнение обозначается Ā

16.

Пересечение и объединение множеств обладают
свойствами:
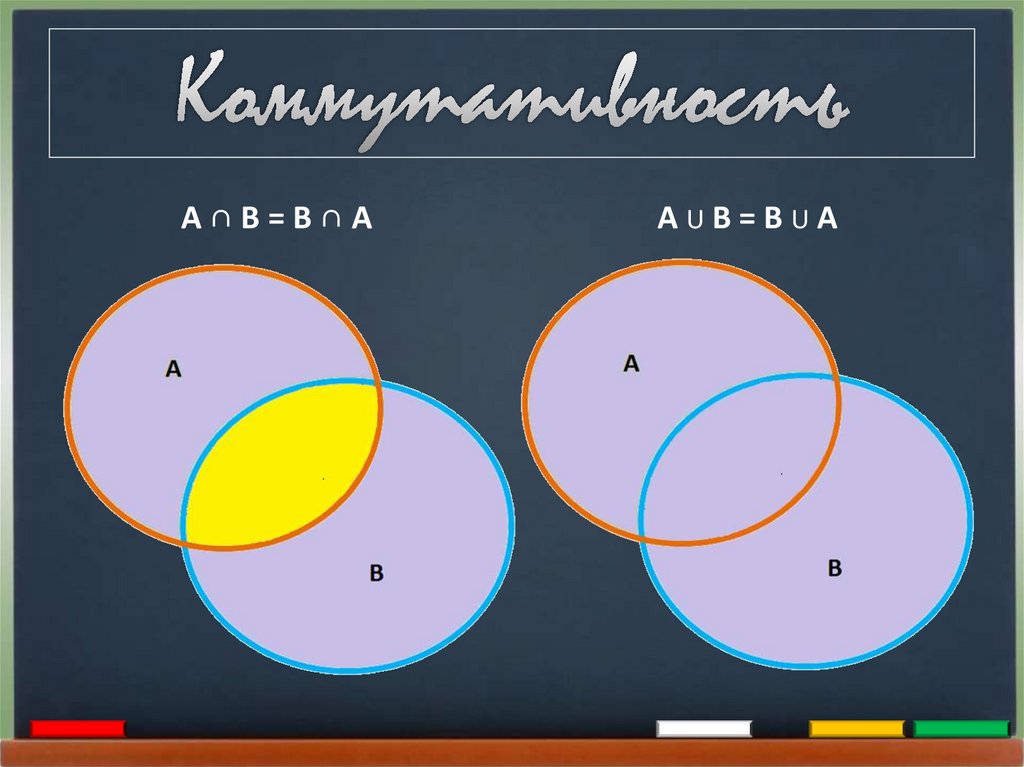
Коммутативность
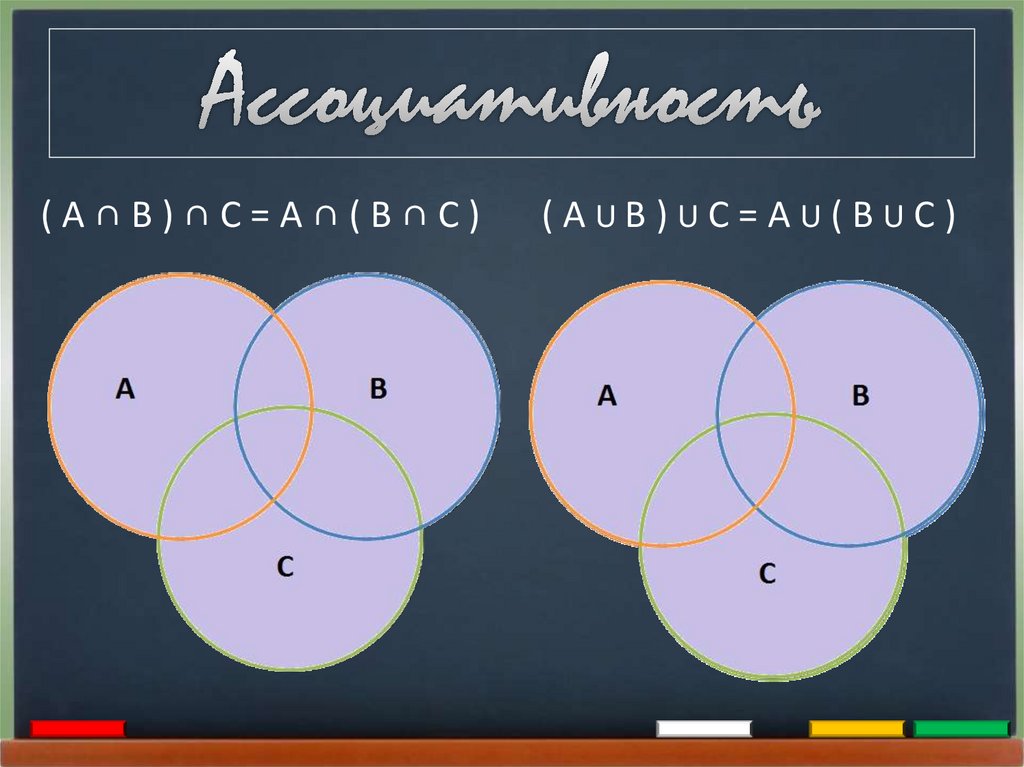
Ассоциативность
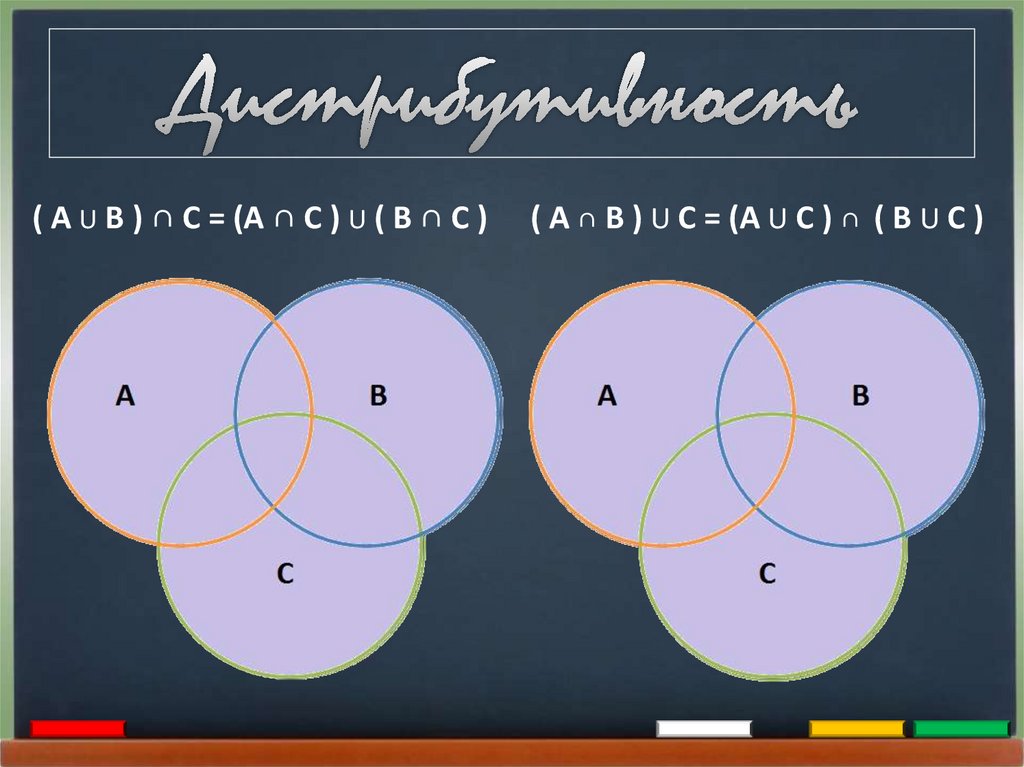
Дистрибутивность

17.

(А∩В)∩С=А∩(В∩С)
(АUВ)UС=АU(ВUС)

18.

А∩В=В∩А
АUВ=ВUА

19.

( А U В ) ∩ С = (А ∩ С ) U ( В ∩ С )
( А ∩ В ) U С = (А U С ) ∩ ( В U С )

20.

В теории множеств рассматриваются отношения между
множествами:
Тождественность. Если каждый элемент множества А является
также и элементом множества В , и каждый элемент множества В
есть также элементом множества А, то эти множества
тождественны. Обозначается так : А=В.
Эквивалентность. Соответствие между элементами множеств А и
В, при котором каждому элементу множества А соответствует
единственный элемент множества В, и наоборот, различным
элементам одного множества соответствуют различные элементы
другого множества, называется взаимно однозначными. Если
существует, по крайней мере, одно взаимно однозначное
соответствие между элементами множеств А и В, то такие
множества называются эквивалентными.

21.

Отношение эквивалентности обладает следующими свойствами:
Симметричность(взаимность). Если множество А эквивалентно
множеству В , то множество В эквивалентно множеству А.
А~В, В~А
Транзитивность ( переходность) . Если множество А эквивалентно
множеству В , а множество В эквивалентно множеству С, то множества А
и С эквивалентны.
А~В, В~С, А~ С.
Рефлексивность ( возвратность). Всякое множество эквивалентно самому
себе.
А~А
Использование отношения эквивалентности позволяет разбить
всевозможные множества на классы эквивалентных между собой множеств.