Similar presentations:
Определение и общие свойства алгоритмов (лекция 1.1)
1.
Технологии проектированияпрограммного обеспечения
информационных систем
Денис Викторович Новицкий
кандидат физ.-мат. наук
зав. центром «Нанофотоника»
Института физики НАН Беларуси
1
2.
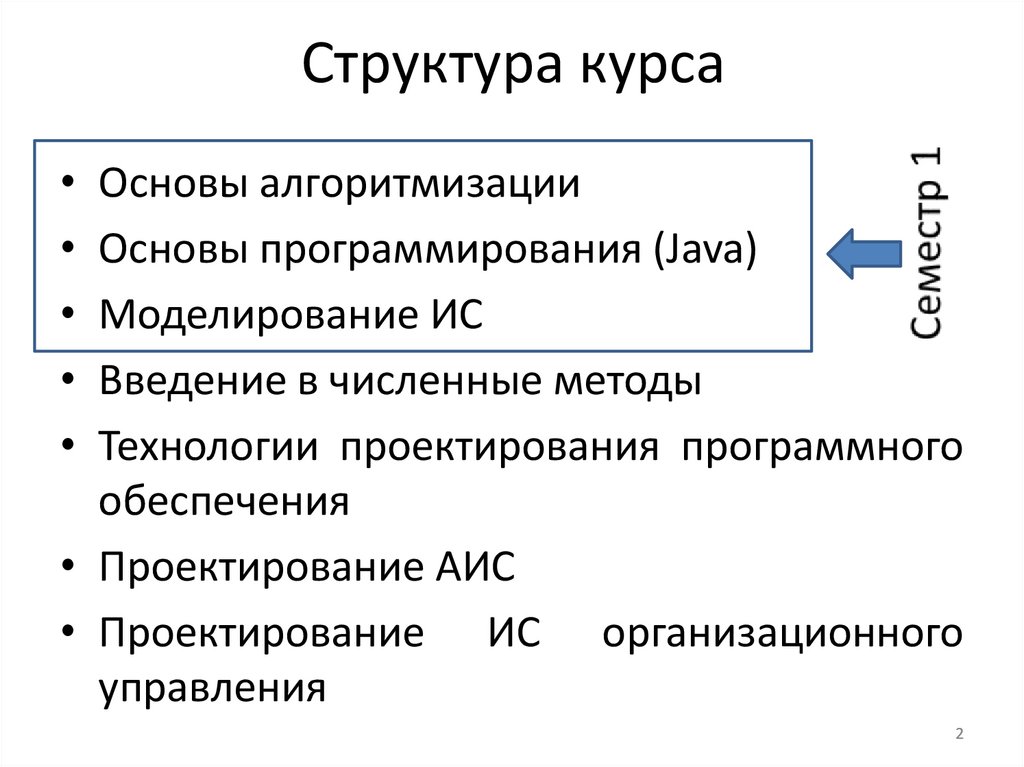
Структура курса• Основы алгоритмизации
• Основы программирования (Java)
• Моделирование ИС
• Введение в численные методы
• Технологии проектирования программного
обеспечения
• Проектирование АИС
• Проектирование ИС организационного
управления
2
3. Раздел 1 Основы алгоритмизации
Литература* Кормен Т.Х. Алгоритмы: Вводный курс. – М.: Вильямс,
2014.
* Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы:
Построение и анализ. – 3-е изд. – М.: Вильямс, 2013.
* Кнут Д. Искусство программирования. Т.1: Основные
алгоритмы. – 3-е изд. – М.: Вильямс, 2006.
3
4. Лекция 1.1 Определение и общие свойства алгоритмов
45. Определение алгоритма
Алгори́тм — набор инструкций, описывающихпорядок действий исполнителя для достижения
некоторого результата.
Неформальное определение: Алгоритм — это любая
корректно определенная вычислительная процедура,
на вход (input) которой подается некоторая величина
или набор величин и результатом выполнения которой
является выходная (output) величина или набор
значений. Такие алгоритмы называют также
вычислительными. При корректной реализации для
них предусмотрено окончание работы.
5
6.
Иногда выделяют управляющие алгоритмы, которыепредназначены для взаимодействия с некоторым
объектом управления и призваны обеспечить
корректную выдачу управляющих воздействий в
зависимости
от
складывающейся
ситуации,
отражаемой поступающими от объекта управления
сигналами. В таких алгоритмах может вообще не быть
предусмотрено окончание работы.
6
7. Исполнитель алгоритма
* Компьютер* Механизм
* Человек
7
8. Немного истории
Вычислительные процессы алгоритмическогохарактера были известны еще древним:
арифметические действия над целыми числами,
нахождение наибольшего общего делителя двух
чисел и т. д.
Абу Абдуллах Мухаммед ибн Муса
аль-Хорезми (алгоритм — альХорезми):
825 – Китаб аль-джебр валь-мукабала
(«Книга о сложении и вычитании»);
XII в. – латинский перевод Algoritmi de
numero Indorum («Алгоритмы о счёте
индийском»).
8
9. Немного истории
В последующие века появилось множестводругих трудов со словом algoritmi или
algorismi в названии, посвящённых обучению
искусству счёта с помощью цифр. Со
временем слово algorism (или algorismus)
обрело значение способа выполнения
арифметических
действий
посредством
арабских цифр, то есть на бумаге, без
использования абака (счетной доски).
Постепенно значение слова расширялось, оно
начало применяться не только к сугубо
вычислительным, но и к другим математическим
процедурам:
1360 – Николай Орем опубликовал трактат
Algorismus
proportionum
(«Вычисление
пропорций»), в котором приблизился к открытию
логарифма.
9
10. Немного истории
1684 – Готфрид Вильгельм Лейбниц всочинении Nova Methodvs pro maximis et
minimis, itemque tangentibus… впервые
использовал слово «алгоритм» (Algorithmo) в
ещё
более
широком
смысле:
как
систематический способ решения проблем
дифференциального исчисления.
1765 – Леонард Эйлер в работе
«Использование нового алгоритма для
решения проблемы Пелля» (De usu novi
algorithmi in problemate Pelliano
solvendo) понимает алгоритм уже как
синоним способа решения задачи, что
очень
близко
к
современным
представлениям.
10
11. Немного истории
К началу XX в. все старинные значениявышли из употребления и для
математиков слово «алгоритм» уже
означало любой арифметический или
алгебраический процесс, выполняемый
по строго определённым правилам.
Одновременно происходила экспансия
понятия
алгоритма
из
чистой
математики в другие сферы, что
связано прежде всего с появлением
компьютеров. К 1980-м гг. слово
«алгоритм» вошло во все школьные
учебники информатики и обрело новую
жизнь.
Сегодняшняя известность понятия «алгоритм» напрямую связана со
степенью распространения компьютеров.
11
12. Формальное определение алгоритма
Понятие алгоритма относится к первоначальным, основным, базиснымпонятиям математики, т.е. алгоритм не является точным математическим
понятием. Поэтому его современное определение основывается на ряде
тезисов, или аксиом, которые не могут быть доказаны математическими
методами.
Современное формальное определение вычислительного алгоритма было
дано в 30—50-е годы XX века
Алан Тьюринг
(1912-1954)
Алонзо Чёрч
(1903-1995)
Эмиль Пост
(1897-1954)
Норберт Винер
(1894-1964)
Андрей Марков
(1903-1979)
12
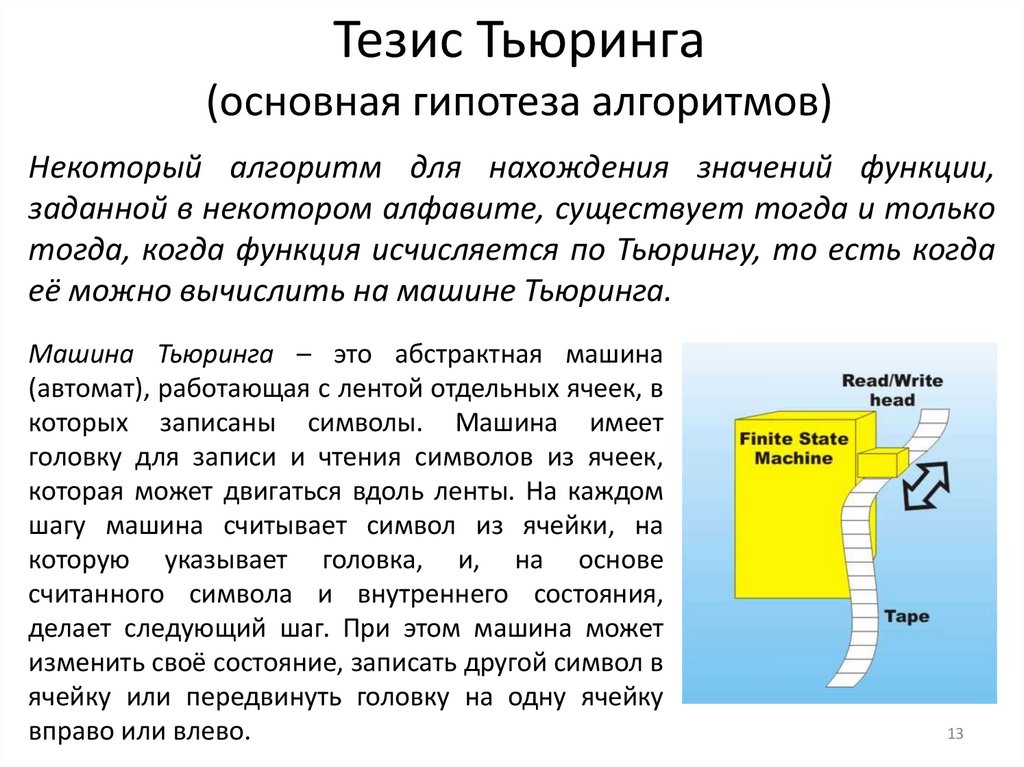
13. Тезис Тьюринга (основная гипотеза алгоритмов)
Некоторый алгоритм для нахождения значений функции,заданной в некотором алфавите, существует тогда и только
тогда, когда функция исчисляется по Тьюрингу, то есть когда
её можно вычислить на машине Тьюринга.
Машина Тьюринга – это абстрактная машина
(автомат), работающая с лентой отдельных ячеек, в
которых записаны символы. Машина имеет
головку для записи и чтения символов из ячеек,
которая может двигаться вдоль ленты. На каждом
шагу машина считывает символ из ячейки, на
которую указывает головка, и, на основе
считанного символа и внутреннего состояния,
делает следующий шаг. При этом машина может
изменить своё состояние, записать другой символ в
ячейку или передвинуть головку на одну ячейку
вправо или влево.
13
14. Тезис Чёрча
Итак, каждому алгоритму можно сопоставить функцию, которую онвычисляет. И эта функция должна вычисляться на машине Тьюринга. Вопрос:
каким функциям можно сопоставить машину Тьюринга, т.е. для каких
функций существует алгоритм?
Исследование этих вопросов привело к созданию теории рекурсивных
функций. Рекурсивные функции определяются индуктивным образом, т.е.
сначала постулируется, что некоторые функции удовлетворяют требуемому
условию (вычислимы по Тьюрингу, т.е. им сопоставимы машины Тьюринга), а
затем на их основе строятся новые функции того же класса.
Подобно тезису Тьюринга в теории вычислимых функций была выдвинута
гипотеза, которая называется тезисом Чёрча:
Числовая
функция
тогда
и
только
тогда
алгоритмически исчисляется, когда она частично
рекурсивна.
14
15. Принцип нормализации Маркова
Нормальный алгоритм Маркова — это система последовательныхприменений подстановок, которые реализуют определенные процедуры
получения новых слов из базовых, построенных из символов некоторого
алфавита. Нормально вычислимой называют функцию, которую можно
реализовать нормальным алгоритмом, т.е. алгоритмом, который каждое
слово из множества допустимых превращает в исходные значения данной
функции. Любой нормальный алгоритм эквивалентен некоторой машине
Тьюринга.
Создатель теории нормальных алгоритмов Марков выдвинул гипотезу,
которая получила название принцип нормализации Маркова:
Для нахождения значений функции, заданной в
некотором алфавите, тогда и только тогда
существует некоторый алгоритм, когда функция
нормально исчисляемая.
Подобно тезисам Тьюринга и Черча, принцип нормализации Маркова не
15
может быть доказан математическими средствами.
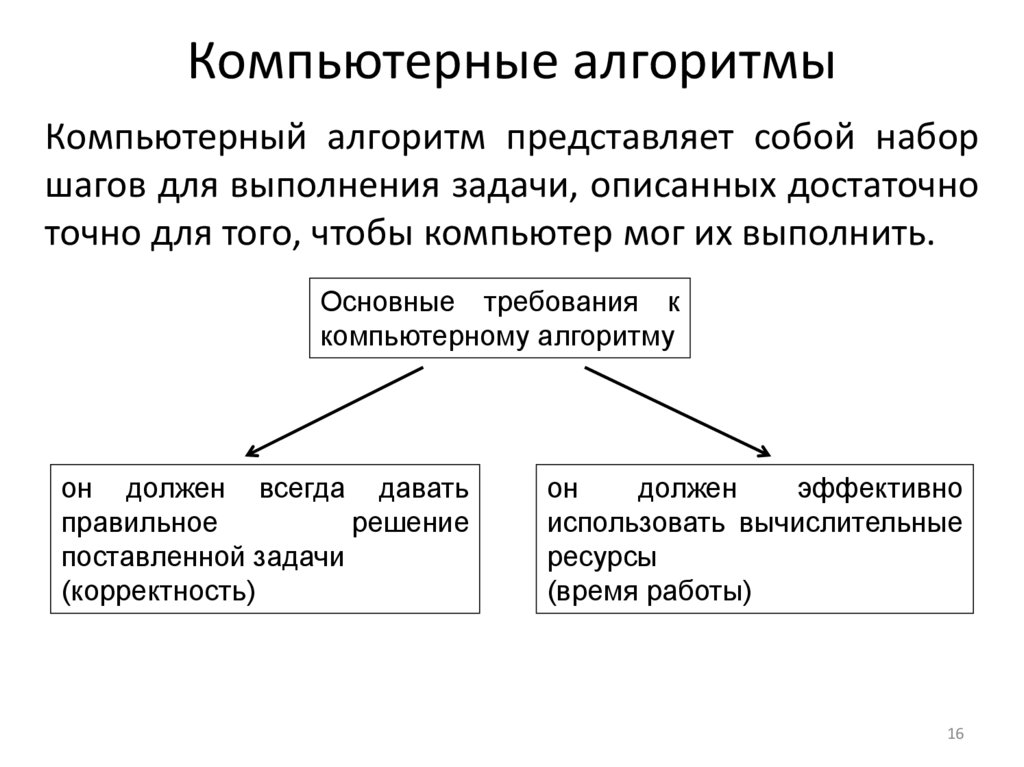
16. Компьютерные алгоритмы
Компьютерный алгоритм представляет собой наборшагов для выполнения задачи, описанных достаточно
точно для того, чтобы компьютер мог их выполнить.
Основные требования к
компьютерному алгоритму
он должен всегда давать
правильное
решение
поставленной задачи
(корректность)
он
должен
эффективно
использовать вычислительные
ресурсы
(время работы)
16
17. Корректность алгоритма
Алгоритм корректен, если для любых входных данных результатом егоработы являются корректные выходные данные.
Говорят, что корректный алгоритм решает данную вычислительную задачу.
Если алгоритм некорректный, то для некоторых входных данных он может
вообще не завершить свою работу или выдать неправильный ответ.
Корректность не зависит от конкретного компьютера, на котором
реализован алгоритм.
Иногда некорректные алгоритмы тоже полезны:
стохастические алгоритмы
(исходные данные + случайные значения)
алгоритмы типа Лас-Вегас
алгоритмы типа Монте-Карло
(всегда дают корректный результат,
но время их работы не определено)
(могут давать неправильные
результаты с известной
вероятностью)
17
18.
Использование ресурсовОдин из основных показателей эффективности – это время работы
алгоритма.
Фактическое время работы алгоритма зависит от нескольких факторов,
внешних по отношению к самому алгоритму:
• от скорости работы компьютера,
• языка программирования, на котором реализован алгоритм,
• компилятора или интерпретатора, который переводит программу в
выполнимый код,
• опыта разрабатывающего программу программиста,
• от того, чем именно параллельно выполнению алгоритма занят
компьютер.
Для получения объективной оценки скорости алгоритма
рассматривается, каким образом время работы зависит
от размера входных данных и как быстро растет время с
ростом размера входных данных.
18
19. Пример: алгоритмы сортировки
Сортировка вставкойВремя работы оценивается как с1n2
Сортировка слиянием
Время работы оценивается как с2nlog2n
Здесь n — количество сортируемых элементов, а с1 и c2 —
константы, не зависящие от n.
работает быстрее для небольшого
количества
сортируемых
элементов
работает быстрее для большого
количества
сортируемых
элементов
Независимо от соотношения коэффициентов с1 и c2, с ростом количества
сортируемых элементов обязательно будет достигнут переломный момент,
когда сортировка слиянием окажется более производительной.
Поэтому вводится порядок роста времени работы
коэффициентов или членов более низкого порядка.
порядок роста — n2
—
без
учета
порядок роста — nlog2n
19
20. Асимптотические обозначения
Θ-обозначения: если у нас имеются две функции, f(n) иg(n), то мы говорим, что f(n) представляет собой Θ(g(n)),
если f(n) при достаточно больших n отличается от g(n)
лишь на постоянный множитель.
Пример: для линейного роста времени мы записываем,
что время работы алгоритма равно Θ(n).
Пример: n2/4 + 100n + 50 = Θ(n2).
Другими
словами,
мы
сосредотачиваемся
на
доминирующем члене, отбрасывая члены более низкого
порядка и постоянные множители.
20
21. Асимптотические обозначения
Вообще говоря, время работы может быть ограничено как сверху, таки снизу некоторыми (возможно, разными) функциями от n.
О-обозначения: функция f(n) является O(g(n)), если при достаточно
больших n функция f(n) ограничена сверху g(n), умноженной на
некоторую константу.
О-обозначения показывают, что время работы никогда не будет хуже,
чем константа, умноженная на некоторую функцию от n.
Пример: Если линейная функция от n — верхняя граница во всех
случаях, то этот факт обозначается как O(n).
Ω-обозначения: функция f(n) представляет собой Ω(g(n)), если, когда n
становится достаточно большим, f(n) ограничена снизу некоторой
константой, умноженной на g(n).
Общим названием для Θ-,
асимптотические обозначения.
О-
и
Ω-обозначений
является
21
22. Пример: Процедура линейного поиска элемента в массиве данных
2223.
Некоторые определенияПроцедура — это алгоритм, ранее разработанный и
целиком
используемый
при
алгоритмизации
конкретной задачи. Когда мы вызываем процедуру,
мы снабжаем ее входными данными -- параметрами
процедуры. Вызов процедуры может сгенерировать
некоторые выходные данные (а может обойтись и без
этого). Если процедура генерирует выходные данные,
мы обычно рассматриваем их как нечто,
передаваемое назад вызывающему процедуру коду
(возврат значения процедурой).
23
24.
Некоторые определенияМассив группирует данные одного и того же типа в
единую сущность. Можно думать о массиве как о
таблице, которая при наличии индекса некоторой
записи позволяет получить элемент массива с
указанным
индексом.
Индексы
в
массиве
представляют собой последовательные числа,
которые могут начинаться с любого числа, но обычно
индексы начинаются с 1.
Будем обозначать конкретный элемент массива с
помощью квадратных скобок: например, i-й элемент
массива A обозначается как A[i].
24
25.
Линейный поискДано: массив А с n элементами.
Выяснить: присутствует ли в массиве А значение х.
Если да, то мы хотим знать индекс i, такой, что A[i] = х.
Если нет – вывести соответствующее сообщение. При
этом x может встретиться в массиве более одного раза.
Пример – поиск книги на полке.
Алгоритм линейного поиска: мы начинаем с начала
массива (первого его элемента), поочередно проверяя
все его элементы (А[1], затем A[2], затем A[3] и так
далее до А[n]) и записывая место, где мы находим x
(если мы вообще находим его).
25
26.
Процедура линейного поискаПроцедура Linear-Search(A,n,x)
Вход:
• A – массив;
• n – количество элементов массива А, среди которых
выполняется поиск;
• x – искомое значение.
Выход: значение переменной answer – либо индекс i,
для которого A[i] = x, либо специальное значение notfound, которое может представлять собой любой
некорректный
индекс
массива,
например,
произвольное отрицательное значение.
26
27.
Шаги процедуры:1. Установить значение answer равным not-found.
2. Для каждого индекса i, пробегающего поочередно
значения от 1 до n:
А. Если A[i] = x, установить значение answer
равным i.
3. В качестве выходного вернуть значение answer.
27
28. Цикл
На шаге 2 рассмотренного алгоритма выполняются некоторыенеоднократные действия. Такая ситуация называется циклом, а каждое
однократное выполнение этих действий – итерацией цикла.
При этом происходит следующая последовательность действий:
1) переменная цикла (в данном случае — i) получает начальное значение (в
данном случае — 1),
2) значение переменной цикла сравнивается с пределом (в данном случае
— n),
3) если текущее значение переменной цикла не превышает предел,
выполняется все, что указано в теле цикла (в данном случае это строка 2А),
4) выполняется инкремент переменной цикла — т.е. прибавление к ней 1,
5) возврат к этапу 2, где новое значение переменной цикла сравнивается с
пределом.
Действия повторяются многократно, пока значение переменной цикла не
превысит предел.
Цикл вида "для i = 1 до n" выполняет n итераций и n+1 проверку на
превышение значения предела.
28
29. Время работы линейного поиска
(как функция количества n элементов массива A)Обозначим:
• t1 и t3 – времена выполнения шагов 1 и 3 (запускаются один раз),
• t21 – время на сравнение i с n на шаге 2 (выполняется n+1 раз),
• t22 – время на увеличение i на шаге 2 (выполняется n раз),
• t2A1 – время, требующееся для проверки A[i] = x на шаге 2А (выполняется n
раз),
• t2A2 – время, необходимое для присваивания переменной answer значения i.
Тогда нижняя граница времени поиска (нет ни одного элемента со
значением, равным x):
t1 t 21 (n 1) t 22 n t 2 A1 n t 2 A2 0 t3 (t 21 t 22 t 2 A1 ) n (t1 t 21 t3 )
Верхняя граница времени поиска (значение всех элементов равно x):
t1 t 21 (n 1) t 22 n t 2 A1 n t 2 A2 n t3 (t 21 t 22 t 2 A1 t 2 A2 ) n (t1 t 21 t3 )
Время работы процедуры Linear-Search ограничено линейной функцией от
n как снизу, так и сверху.
Время работы алгоритма равно Θ(n).
29
30.
Улучшенный линейный поискПрекращаем поиск, как только он находит в
массиве значение x.
Процедура Better-Linear-Search(A,n,x)
Вход и выход: те же, что и в Linear-Search.
Шаги процедуры:
1. Для i = 1 до n:
А. Если A[i] = х, вернуть значение i в качестве
выхода процедуры.
2. Вернуть в качестве выходного значение not-found.
30
31.
Оценка времени работы сложнее, поскольку неизвестно, сколько раз будет выполняться итерация
цикла. В наихудшем случае (перебор всех элементов)
процедура Better-Linear-Search требует время Θ(n). В
наилучшем случае (A[1] = x) процедура завершает
работу уже после первой итерации и потому требует
только постоянного количества времени Θ(1).
Таким образом, для процедуры Better-Linear-Search
верхней границей времени работы во всех случаях
является О(n), а нижней границей – Ω(1).
31
32.
Поиск с ограничителемЦель – избежать двойной проверки (i<n и A[i]=x) при
каждой итерации цикла. Для этого поместим искомое
значение x в последнюю позицию А[n] после
сохранения содержимого A[n] в другой переменной.
Когда мы находим x, мы выполняем проверку,
действительно ли мы его нашли или просто достигли
конца массива. Значение, которое мы помещаем в
массив, называется ограничителем.
32
33.
Процедура Sentinel-Linear-Search(A,n,x)Вход и выход: те же, что и в Linear-Search.
Шаги процедуры:
1. Сохранить А[n] в переменной last и поместить х в
А[n].
2. Установить i равным 1.
3. Пока А[i] ≠ x, увеличивать i на 1.
4. Восстановить А[n] из переменной last.
5. Если i < n или A[n] = x, вернуть значение i в качестве
выхода процедуры.
6. В противном случае вернуть в качестве
возвращаемого значения not-found.
33
34. Инвариант цикла
Один из распространенных методов показа правильностициклического алгоритма использует инвариант цикла -логическое утверждение, для которого демонстрируется
истинность в начале каждой итерации цикла.
Чтобы инвариант цикла помог доказать корректность алгоритма,
мы должны показать выполнение трех его свойств:
а) Инициализация. Инвариант цикла истинен перед первой
итерацией цикла.
б) Сохранение. Если инвариант цикла истинен перед итерацией
цикла, он остается истинным и после нее.
в) Завершение. Цикл завершается, а после его завершения
инвариант цикла вместе с причиной завершения цикла дают нам
искомую цель работы алгоритма.
34
35.
Инвариант цикла для процедуры Better-Linear-Search: «В началекаждой итерации на шаге 1, если x имеется в массиве А, то он
находится в подмассиве (непрерывной части массива) с
элементами от A[i] до А[n]».
а) Инициализация. При i = 1 подмассив в инварианте цикла есть
весь массив полностью.
б) Сохранение. Предположим, что в начале итерации i, если x
имеется в массиве А, то он присутствует в подмассиве от
элемента A[i] до элемента А[n]. Если эта итерация выполняется
без возврата значения, то A[i]≠x, и, следовательно, если x
присутствует в массиве А, то он находится в подмассиве от
элемента A[i +1] до элемента А[n]. Поскольку i перед следующей
итерацией увеличивается на единицу, инвариант цикла будет
выполняться.
35
36.
в) Завершение. Цикл должен завершаться либо потому, чтопроцедура вернет некоторое значение, либо потому, что
выполнится условие i > n. Первый случай очевиден. Чтобы
разобраться со случаем завершения цикла по условию i > n,
рассмотрим обратную форму утверждения (его контрапозицию).
Контрапозицией инварианта цикла является утверждение "если x
отсутствует в подмассиве от A[i] до А[n], то его нет и в массиве А".
Теперь, когда i > n, подмассив от A [i] до А [n] пуст, в нем нет ни
одного элемента, так что он никак не может содержать x. В силу
контрапозиции инварианта цикла x отсутствует в массиве А, так
что возврат значения not-found является корректным.
Контрапозицией утверждения "если А, то Б" является
утверждение "если не Б, то не А". Контрапозиция истинна
тогда и только тогда, когда истинно исходное утверждение.
36
37. Рекурсивное построение алгоритмов
С помощью рекурсии мы решаем задачу путем решенияменьших экземпляров этой же задачи. Чтобы рекурсия
работала, должны выполняться два свойства:
1) должен существовать один или несколько базовых
случаев, когда вычисления проводятся непосредственно,
без рекурсии;
2) каждый рекурсивный вызов процедуры должен быть
меньшим экземпляром той же самой задачи, так что в
конечном итоге будет достигнут один из базовых случаев.
Пример: алгоритм вычисления факториала
Как известно, n! определяется как 0!=1 и n! n (n 1) ... 2 1
Очевидно, что n! n ( n 1)!
37
38. Факториал: Корректный рекурсивный алгоритм
Процедура Factorial(n)Вход: целое число n ≥ 0.
Выход: значение n!.
Шаги процедуры:
1. Если n = 0, вернуть 1 в качестве возвращаемого
значения.
2. В противном случае вернуть n, умноженное на
значение, которое возвращает рекурсивно вызванная
процедура Factorial(n-1).
38
39.
Базовый случай здесь осуществляется при n = 0, икаждый рекурсивный вызов выполняется для
значения n, уменьшенного на 1.
В случае, когда исходное значение больше нуля,
рекурсивные вызовы в конечном счете придут к
базовому случаю, т.е. рекурсивный вызов должен
выполняться для меньшего экземпляра задачи.
39
40. Факториал: Некорректный рекурсивный алгоритм
Процедура Bad-Factorial(n)Вход и выход: те же, что и для Factorial.
Шаги процедуры:
1. Если n = 0, вернуть 1 в качестве возвращаемого
значения.
2. В противном случае вернуть Bad-Factorial(n+1)/(n+1).
Математически здесь все корректно, но построенная по этой
формуле рекурсивная процедура не дает правильный ответ, т.к.
рекурсивный вызов выполняется для большего экземпляра
задачи. В результате эта процедура никогда бы не добралась до
базового случая, когда n = 0, а компьютер выдал бы сообщение
типа "ошибка переполнения стека".
40
41.
Рекурсивный вариант линейного поискаПроцедура Recursive-Linear-Search(A,n,x,i)
Вход: тот же, что и для Linear-Search, но с
дополнительным параметром i.
Выход: индекс элемента, равного х, в подмассиве от
элемента А[i] до А[n], или значение not-found, если х
в этом подмассиве отсутствует.
Шаги процедуры:
1. Если i > n, вернуть not-found.
2. В противном случае (i < n), если A[i] = x, вернуть i.
3. В противном случае (i < n и A[i] ≠ x), вернуть
Recursive-Linear-Search(A,n,x,i +1).
41
42.
Базовый случай осуществляется на шаге 1, когдаподмассив пуст, т.е. когда i > n.
Поскольку на каждом шаге значение i увеличивается
на единицу при каждом рекурсивном вызове, если
ни один из вызовов не вернет значение i на шаге 2, в
конечном итоге i превысит n, и будет достигнут
базовый случай рекурсии.
42
43.
Можно ли еще улучшить алгоритмпоиска?
В общем случае – нет, так что в наихудшем случае мы
не достигнем лучшего времени, чем Θ(n).
Улучшение возможно, только если мы кое-что знаем о
порядке элементов в массиве.
Предположим,
что
массив
отсортирован
в
неубывающем порядке, т.е. каждый элемент массива
меньше или равен элементу, следующему в массиве за
ним, согласно некоторому определению отношения
"меньше, чем":
• Для чисел очевидно,
• Для строк – лексикографический порядок.
43
44.
Бинарный поискИдея: В любой момент мы рассматриваем
только подмассив, т.е. часть массива между
двумя индексами (включительно). Назовем их
р и r, причем первоначально р = 1 и r = n. Мы
многократно делим подмассив пополам, до тех
пор, пока не произойдет одно из двух событий:
либо мы найдем искомое значение, либо
подмассив окажется пустым (р > r).
44
45.
• Пусть мы ищем значение х в массиве А. На каждомшаге
мы
рассматриваем
только
подмассив,
начинающийся с элемента А[р] и заканчивающийся
элементом А[r] – обозначим его A[р..r].
• На каждом шаге вычисляем средину q подмассива,
вычисляя среднее как q ( p r ) / 2
• Если A[q] = x, то искомый элемент найден.
• Если A[q] != x, то…
45
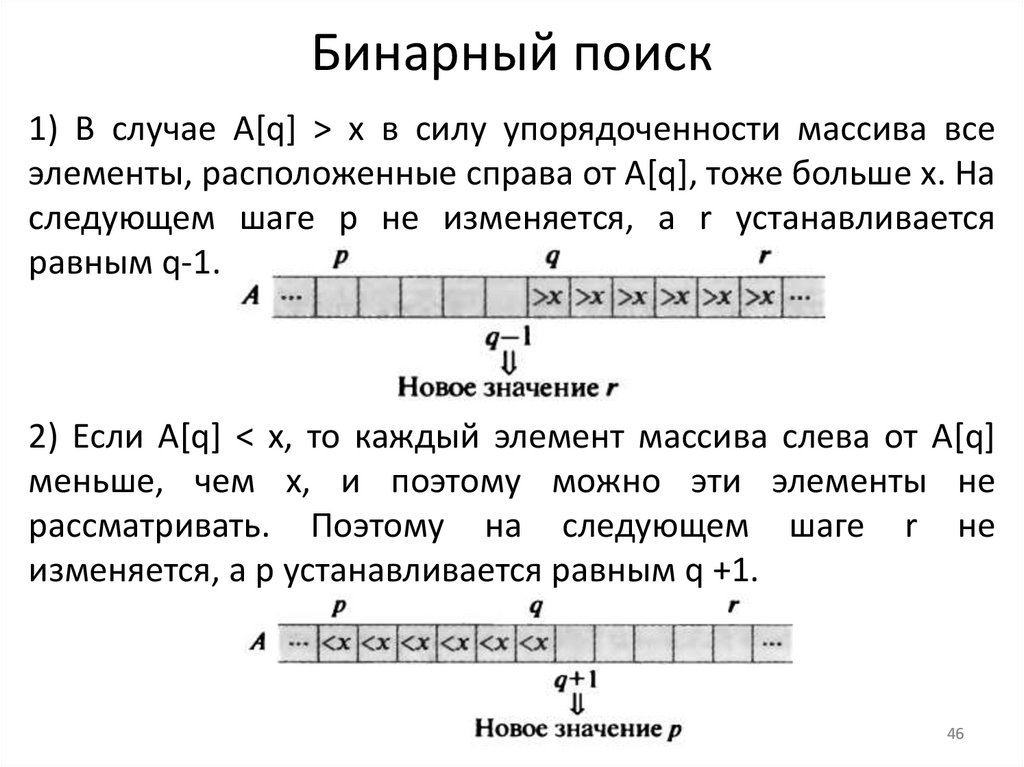
46.
Бинарный поиск1) В случае A[q] > x в силу упорядоченности массива все
элементы, расположенные справа от A[q], тоже больше x. На
следующем шаге p не изменяется, а r устанавливается
равным q-1.
2) Если A[q] < x, то каждый элемент массива слева от A[q]
меньше, чем x, и поэтому можно эти элементы не
рассматривать. Поэтому на следующем шаге r не
изменяется, а p устанавливается равным q +1.
46
47.
Алгоритм бинарного поискаПроцедура Binary-Search(A,n,x).
Вход и выход: те же, что и в Linear-Search.
Шаги процедуры:
1. Установить р равным 1, а r равным n.
2. Пока р ≤ r, выполнять следующие действия.
A. Установить q равным q ( p r ) / 2
B. Если A[q] = x, вернуть q.
C. В противном случае (A[q] != x), если A [q] > x,
установить r равным q-1.
D. В противном случае (A[q] < х) установить p
равным q+1.
3. Вернуть значение not-found.
47
48.
Рекурсивный вариант бинарногопоиска
Процедура Recursive-Binary-Search(A,p,r,x).
Вход и выход: входные параметры А и х те же, что и у процедуры
Linear-Search, также, как и выход. Входные параметры p и r
определяют обрабатываемый подмассив A[р..r].
Шаги процедуры:
1. Если р > r, вернуть not-found.
2. В противном случае (р < r) выполнить следующие действия.
A. Установить q ( p r ) / 2
B. Если A[q] = x, вернуть q.
C. В противном случае (A[q] != x), если A[q] > x, вернуть
Recursive-Binary-Search(A,p,q-1,x).
D. В противном случае (A[q] < х) вернуть
Recursive-Binary-Search(A,q+1,r,x).
48
49.
Время работы бинарного поиска• Ключевой факт: размер r-p+1 рассматриваемого
подмассива уменьшается примерно вдвое на каждой
итерации цикла.
• Вопрос: сколько итераций цикла, вдвое уменьшающих
рассматриваемый подмассив, нужно выполнить, чтобы
его исходный размер n уменьшился до 1?
• Ответ определяется просто возведением в степень
путем многократного умножения на 2. Если n
представляет собой точную степень 2, то, ответом
является число log2n. Если нет, то отличие от log2n не
более, чем на 1.
49
50.
• Время работы составляет O(log2n) в предположениипостоянного количества времени, затрачиваемого на
каждую итерацию.
• Наихудший случай (значение x в массиве
отсутствует): Θ(log2n).
• Наилучший случай (x обнаруживается на первой
итерации): Θ(1).
Бинарный поиск работает быстрее, чем
линейный [O(log2n)<O(n)], однако требует
предварительной сортировки массива.
50














































 programming
programming








