Similar presentations:
Алгоритмическая торговля. Научный подход
1.
Алгоритмическая торговляНаучный подход
Ведущий курса:
Александр Горчаков
1
2.
Алгоритмическая торговляНаучный подход
Ведущий курса:
Александр Горчаков
2
3.
Принципы построенияторговых алгоритмов
3
4. Самофинансируемый торговый алгоритм
Yt – многомерная наблюдаемая случайнаявеличина (входные данные алгоритма)
Ct, t=1,2,… – цены, (C0,…,Ct) входит в Yt
Эt=Vt ·Ct+Dt
Самофинансируемый портфель
(Vt+1-Vt)·Сt+1+Dt+1-Dt=0
Эt+1- Эt=Vt+1·Ct+1+Dt+1- Vt·Ct-Dt=Vt·(Ct+1-Ct)
Э0=D0 - начальный капитал;
Vt=V(Yt), t=1,2,…, – торговый алгоритм
4
5. Самофинансируемый торговый алгоритм
Для простоты будем считать, что V(Yt)действительнозначно, а ошибками
округления до целого числа лотов
пренебрежем.
Эt
| V (Yt ) | a
Ct
где а≥1 – параметр, определяемый
маржой, предоставляемой брокером.
5
6. Самофинансируемый торговый алгоритм
ЭtV (Yt ) r (Yt ) a
Ct
, 0 ≤ | r(Yt)| ≤1.
Эt 1 Эt
Ct 1 Ct
a r (Yt )
a r (Yt ) d t 1
Эt
Ct
Условное среднее доходности торгового
алгоритма за один шаг равно
а·r(Yt)·E(dt+1/Yt),
а условная дисперсия
(а·r(Yt))2·D(dt+1/Yt),
6
7. Самофинансируемый торговый алгоритм
M=Er(Yt)·E(dt+1/Yt),D=E(r(Yt))2·D(dt+1/Yt).
1. M→max
r(Yt)=sign(E(dt+1/Yt)) и М=E|E(dt+1/Yt)|,
D=Δ=EI(E(dt+1/Yt)≠0)·D(dt+1/Yt),
Построение стратегии с максимальной средней
доходностью за один шаг сводится к задаче различения
гипотезы sign(E(dt+1/Yt))≠0 против альтернативы
sign(E(dt+1/Yt)) =0. Отметим, что если в данном
критерии используется несмещенная статистика для
sign(E(dt+1/Yt)), то средняя доходность такой
стратегии будет равна максимально возможной, а
дисперсия вырастет «пропорционально» ошибке
критерия.
«Пропорциональность» взята в кавычки неслучайно, так как требует введения
дополнительных условий.
7
8. Самофинансируемый торговый алгоритм
2. M→max при D=z2Δ, 0≤z≤1| E (d t / Yt ) |
m
sign ( E (d t / Yt ), при
a D(d t / Yt )
r (Yt , m)
0, в противном случае
D(m)=E(r(Yt,m))2·D(dt+1/Yt)
D(m) невозрастающая ограниченная
непрерывная слева функция на отрезке от 0 до
+∞ и D(0)=Δ, а D(+∞)=0. Если существует
такое m, что D(m)=z2Δ, то найденная
стратегия и будет иметь максимальное М.
8
9. Самофинансируемый торговый алгоритм
Если z2Δ находится внутри разрыва функцииD(m), то максимум М достигается на
стратегии
| E (d t / Yt ) |
sign ( E (d t / Yt ), при a D(d / Y ) m
t
t
| E (d t / Yt ) |
z 2 D ( m)
r (Yt , m) sign ( E (d t / Yt )
, при
m
D ( m ) D ( m)
a D(d t / Yt )
| E (d t / Yt ) |
m
0, при
a D(d t / Yt )
9
10. Самофинансируемый торговый алгоритм
3. M→max и для любого Yt D(dt/Yt)≤z2Δ,0≤z≤1
z2
sign ( E (dt / Yt ), при D(d / Y ) 1
t
t
r (Yt )
2
2
z
z
sign ( E (d / Y )
, при
1
t
t
D(dt / Yt )
D(dt / Yt )
10
11. Самофинансируемый торговый алгоритм
ВыводыОптимальный торговый алгоритм должен
быть основан на:
- несмещенной оценке знака будущего
приращения цены;
- встроенном, а не внешнем, money
management, в свою очередь основанном на
оценке дисперсии будущего процентного
приращения цены.
11
12. Приращения логарифмов цен
dtVS
Сt 1
ht Ln
Сt
2
t
n
t
d
n 1 d
ht d t
... ( 1)
..., | d t | 1
2
n
12
13. Статистические зависимости
ПустьР(ht+1/Yt+1)= Р(ht+1/ht)
r
ht
r
1. Р (h t =r)=(1+δ)/2, δ ≠ 0,
h t и ht+1 - независимы,
2. Р (ht=r)=½,
Р(sign(h t )= sign(h t+1)=(1+δ)/2,
δ ≠ 0.
13
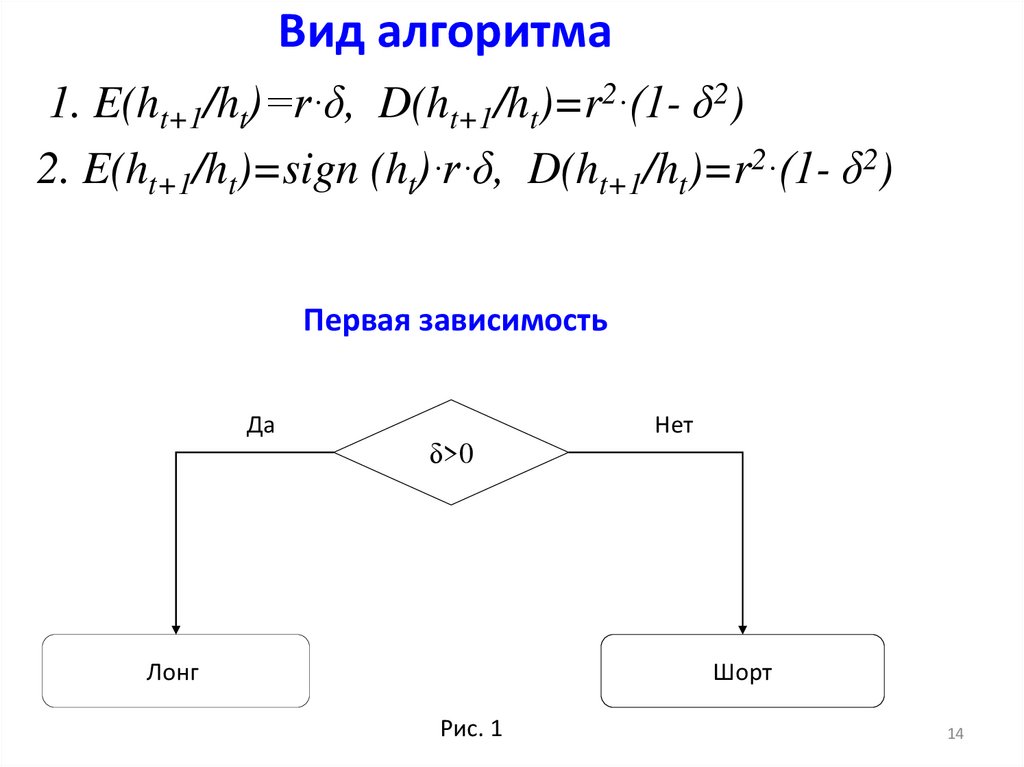
14. Вид алгоритма
1. E(ht+1/ht)=r·δ, D(ht+1/ht)=r2·(1- δ2)2. E(ht+1/ht)=sign (ht)·r·δ, D(ht+1/ht)=r2·(1- δ2)
Первая зависимость
Да
δ>0
Лонг
Нет
Шорт
Рис. 1
14
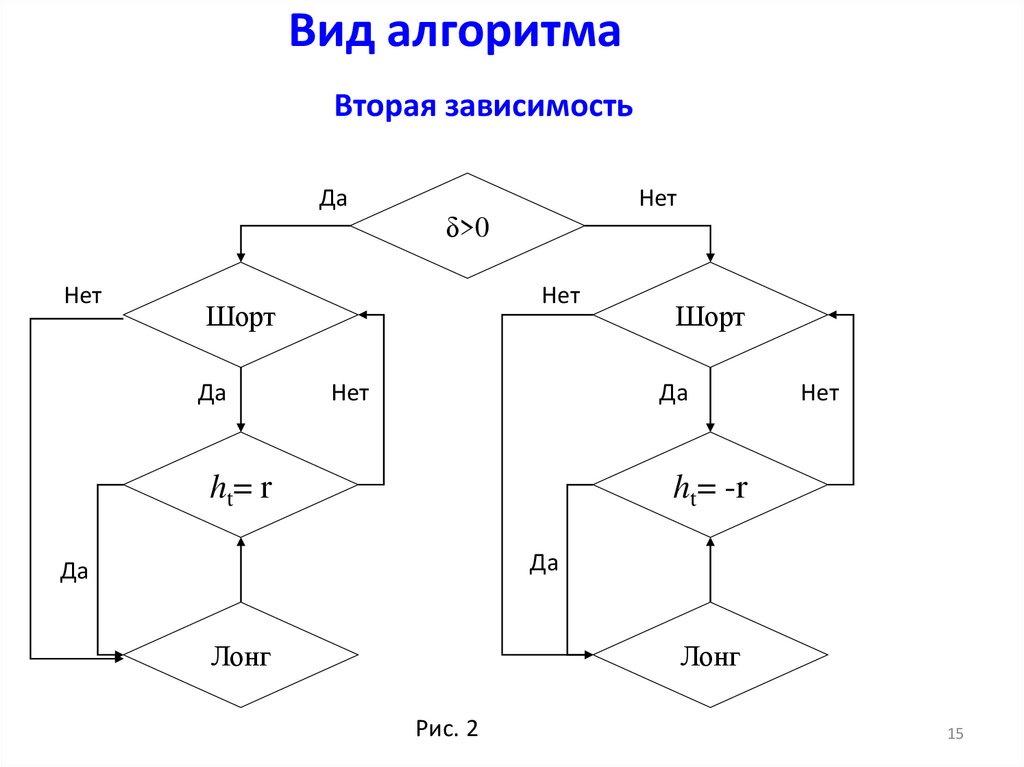
15. Вид алгоритма
Вторая зависимостьДа
Нет
δ>0
Нет
Шорт
Да
Нет
Нет
Шорт
Да
ht= r
Нет
ht= -r
Да
Да
Лонг
Лонг
Рис. 2
15
16. Оптимальные алгоритмы
Ограничение дисперсии за один шагозначает торговлю на долю капитала z.
Как мы уже отмечали выше,
оптимальный алгоритм в данных условиях
представляет собой игру в «бросание
монетки» с вероятностью выигрыша
(1+|δ|)/2 . Это позволяет строить
оптимальные схемы усреднения позиции
для более «хитрых» характеристик риска –
просадки счета и n%СVAR доходности.
16
17. Принципы построения алгоритма
Предположим, что приращения логарифмов ценразбиваются на отрезки, на которых выполнены
вышеуказанные условия.
Задача построения торгового алгоритма сводится к
задачам:
• оценки длин отрезков;,
• определения вида зависимости – 1 или 2;
• определения знака величин δ для каждого отрезка;
• оценки значений |δ| в случае применения техники
усреднения.
В теории вероятностей эта задача называется
«задачей о разладке». Ее особенностью для построения
торговых алгоритмов является то, что, как правило, ее
решение приходится искать в условиях «малых
выборок».
17
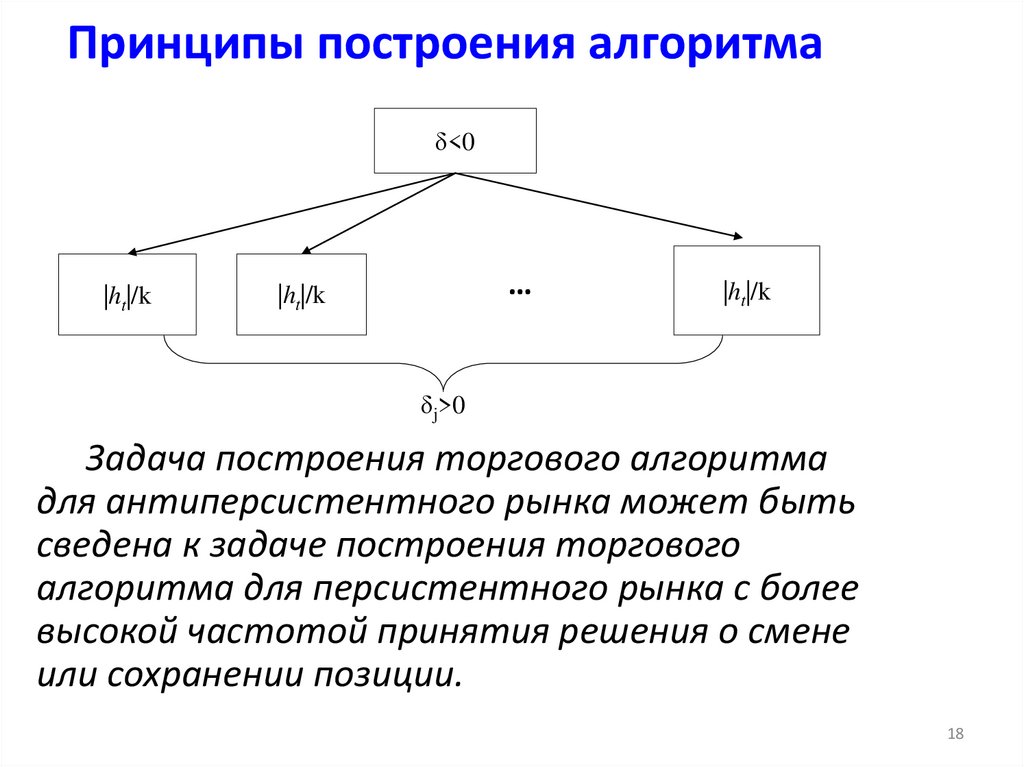
18. Принципы построения алгоритма
δ<0|ht|/k
…
|ht|/k
|ht|/k
δj>0
Задача построения торгового алгоритма
для антиперсистентного рынка может быть
сведена к задаче построения торгового
алгоритма для персистентного рынка с более
высокой частотой принятия решения о смене
или сохранении позиции.
18
19. Краткие выводы
Любой торговый алгоритм является явным или неявным
статистическим прогнозом будущих приращений цен
(логарифмов цен) или функций от них;
Некорректно оценивать эффективность алгоритма только по
одному параметру – доходности за весь период работы;
Построение торговых алгоритмов возможно только в условиях
наличия зависимости между входной информацией и
приращениями цен (логарифмов цен);
В случаев наличия в приращениях логарифмов цен (или
функций от них) участков со стационарной персистентностью
(антиперсистентностью) задача построения торгового
алгоритма сводится к известной в теории вероятностей «задаче
о разладке» на малых выборках;
Задача построения торгового алгоритма для
«антиперсистентного» отрезка рынка может быть сведена к
задаче построения торгового алгоритма для рынка с
«персистентными» отрезками, но с более высокой частотой
принятия решения о смене или сохранении позиции.
19
20. План дальнейших занятий
• «Точка опоры»• Модели цен
• Примеры торговых алгоритмов
20
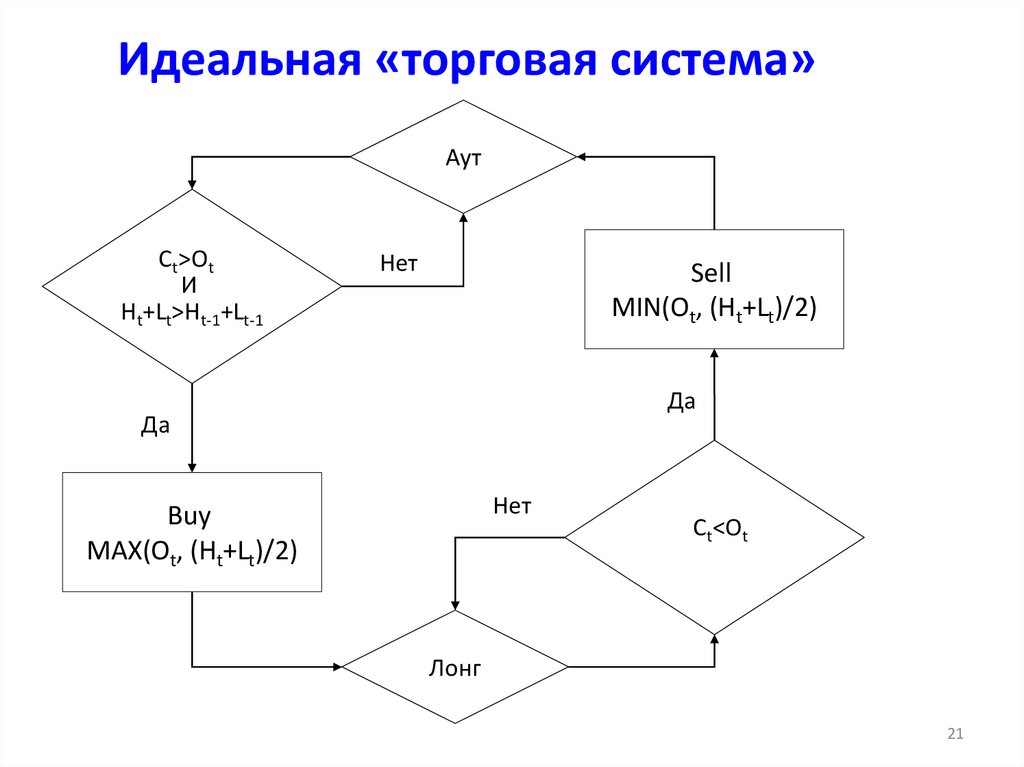
21. Идеальная «торговая система»
АутСt>Ot
И
Ht+Lt>Ht-1+Lt-1
Нет
Sell
MIN(Ot, (Ht+Lt)/2)
Да
Да
Нет
Buy
MAX(Ot, (Ht+Lt)/2)
Ct<Ot
Лонг
21
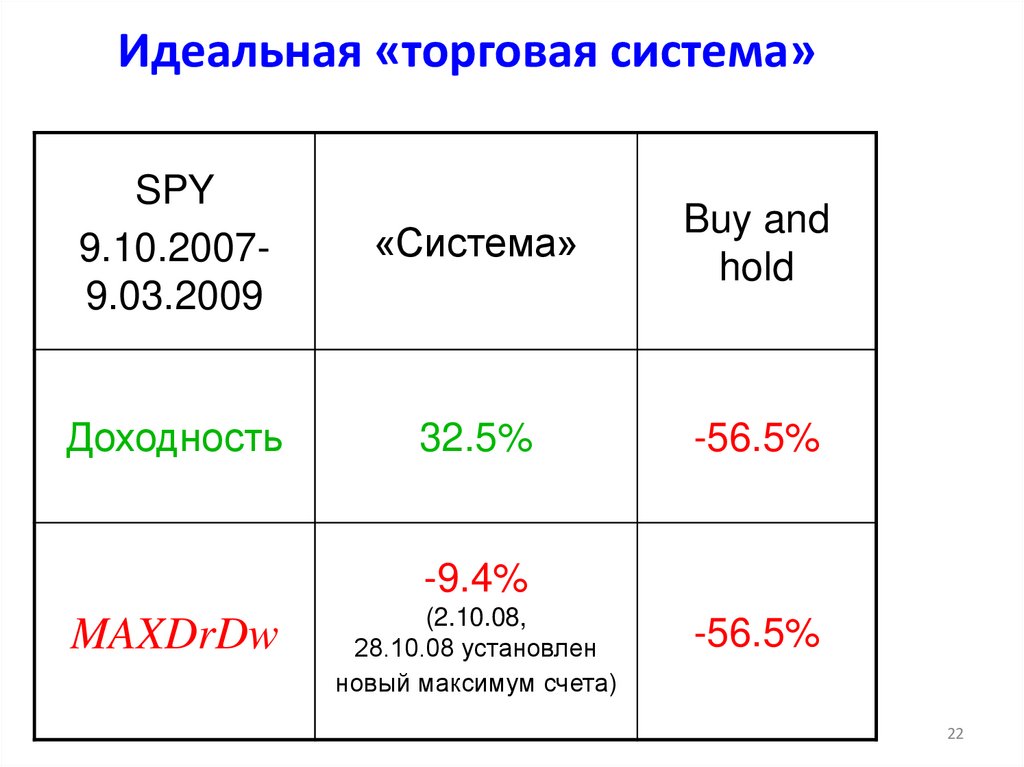
22. Идеальная «торговая система»
SPY9.10.20079.03.2009
«Система»
Buy and
hold
Доходность
32.5%
-56.5%
-9.4%
MAXDrDw
(2.10.08,
28.10.08 установлен
новый максимум счета)
-56.5%
22
23.
Модели цен23
24. Кусочная стационарность
Di, i=1, 2, … - последовательность (вобщем случае ненаблюдаемая)
независимых положительных
целочисленных случайных величин,
принимающих значения больше 1.
n
Тn =
D, T0=0
i 1
i
ht (Ц)=Ln Цt/Цt-1 , Тn-1<t≤Тn – отрезок
некоторой стационарной в узком смысле
последовательности.
24
25. Условная нормальность
ht (C)= Ln Сt/Ct-1=аt+σ·st·nt, где nt ~ N(0,1)Аргументы в пользу этой гипотезы (конкурентный рынок):
Первая разность логарифмов цен ликвидных акций за достаточно
большой промежуток торгов является суммой большого числа первых
разностей логарифмов тиков;
Каждый тик является действием двух или нескольких трейдеров:
трейдера, решившего купить по оферам или продать по бидам и
трейдера (-ов), поставивших эти биды (офера);
Два трейдера, пользующиеся полностью одинаковыми методами
принятия решения – редкость;
Группы трейдеров, использующих «близкие» методы принятия
решения, представляют собой о-малое (как по количеству, так и по
объему средств) от корня из общего числа трейдеров и их объемов
средств;
Любая группа трейдеров, использующих «близкие» методы принятия
решения, не обладает достаточным объемом капитала для
«существенного» изменения цены актива;
Для любого трейдера число трейдеров, использующих независимые
или слабозависимые методы принятия решения, по порядку близко к
множеству всех трейдеров.
25
26. Рынок
27. Конкурентный рынок
Сt 1ht Ln
С
t
ht =аt+σ·st·nt, где nt ~ N(0,1)
Как отличить конкурентный рынок от
неконкурентного?
1. Принять за аксиому, что на каком то активеэталоне он существует.
2. Сравнить статистические свойства ht
конкретного актива и эталона.
Эталон – SPY, период 2005-2012, дневные
приращения логарифмов цен
Конкурентный рынок с высокой
вероятностью
Неконкурентный рынок с
высокой вероятностью
Фьючерс на индекс РТС, Газпром, Магнит, Аптеки 36,6, Ростелеком
Сбербанк
(2006-2010)
27
28. Оптимальный прогноз
Прогнозируем ht+n по Ct+n-1,…,Ct впредположении о многомерной
нормальности ht+n , ht+n-1,…,ht +1
*
n 1
h t n wi ht n i , где
i 1
wi gi (ht n 1 ,..., ht 1 )
29. Оптимальный прогноз
Кусочная стационарностьВременной ряд ht разбивается на случайные
отрезки D0, D1,…, Dm, на каждом из которых ht
представляет собой стационарную гауссовскую
марковскую последовательность.
Если D0, D1,…, Dm, независимы (абсолютно
непредсказуемы), то оптимальный прогноз
является функцией от трех статистик
29
30. Оптимальный прогноз
h индикатор направления движенияt D j
t
h индикатор размаха движения
t D j
2
t
h h индикатор " трендовости" движения
t ,t 1 D j
t t 1
При построении прогноза на основе этих
индикаторов ошибка пропустить «разладку»
там, где она была, опасней ошибки найти
«разладку» там, где ее не было.
30
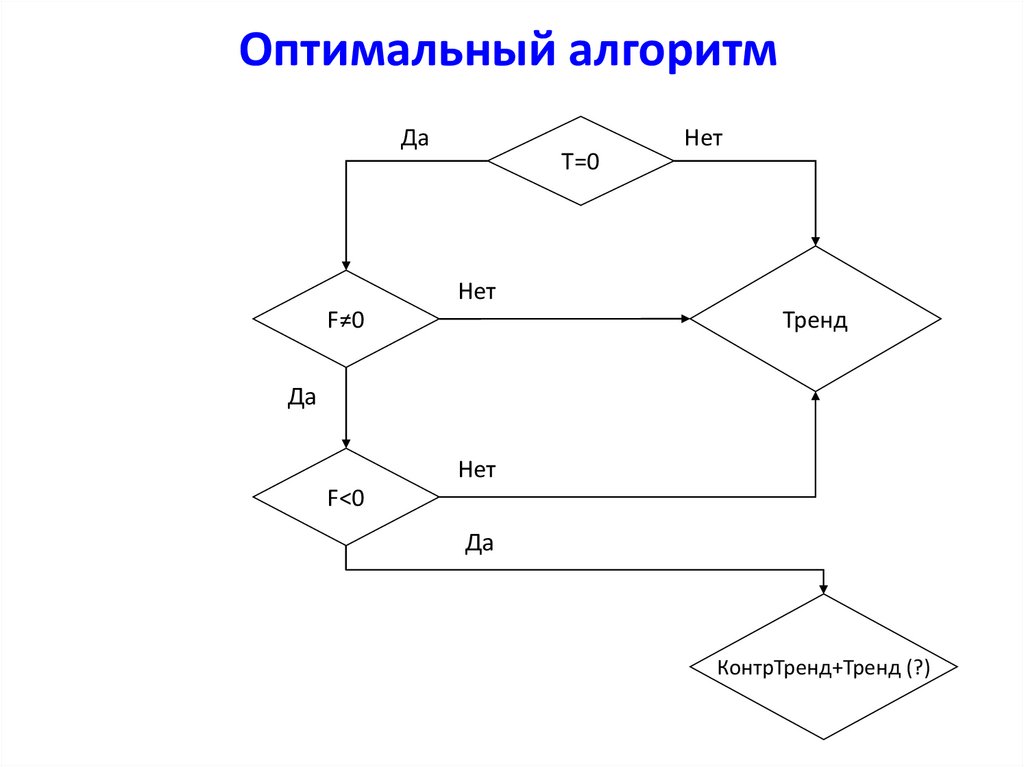
31. Оптимальный алгоритм
ДаT=0
Нет
Нет
Тренд
F≠0
Да
Нет
F<0
Да
КонтрТренд+Тренд (?)
32. Условно нормальные модели
Условно нормальная модель (УНМ)nt ~ N(0,1)- последовательность
независимых случайных величин;
nt и (аt , st ) –независимые друг от друга
последовательности случайных величин.
(аt , st ), Тn-1<t≤Тn – отрезок
стационарной в узком смысле
последовательности двумерных
случайных величин.
32
33. Условно нормальные модели
Кусочно-постоянная модель (КПМ)аt=Аn =const и st=Sn=const для Тn-1<t≤Тn,
где Аn , Sn – ненаблюдаемые
последовательности случайных величин.
Кусочно-марковская модель (КММ)
аt , Тn-1<t≤Тn, - отрезок стационарной
марковской последовательности с Еаi=0.
st=Sn=const для Тn-1<t≤Тn.
Совместная модель (КПММ)
аt , Тn-1<t≤Тn, удовлетворяет одному из
вышеперечисленных условий.
Замечание. Варьируя параметры предложенных моделей, мы можем получать
последовательности случайных величин с одномерным распределением, имеющим
«хвосты любой тяжести», и с любой АКФ, включая нулевую.
33
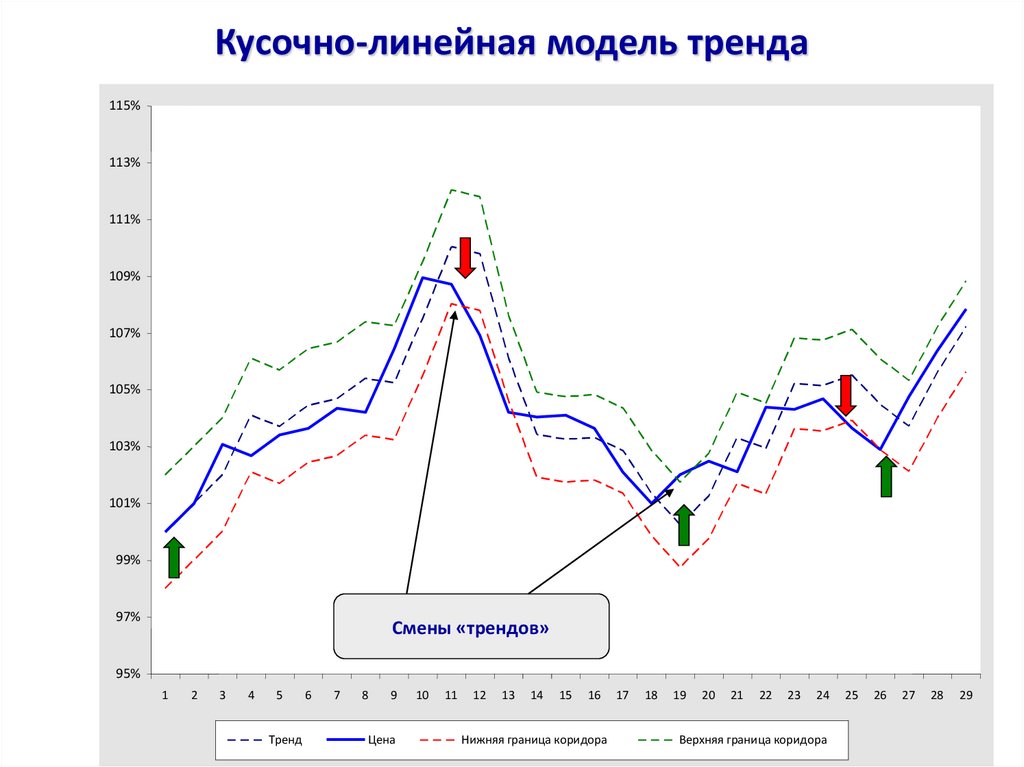
34. Кусочно-линейная модель тренда
115%113%
111%
109%
107%
105%
103%
101%
99%
97%
Смены «трендов»
95%
1
2
3
4
5
Тренд
6
7
8
9
Цена
10
11
12
13
14
15
16
Нижняя граница коридора
17
18
19
20
21
22
23
24
Верхняя граница коридора
25
26
27
28
29
34
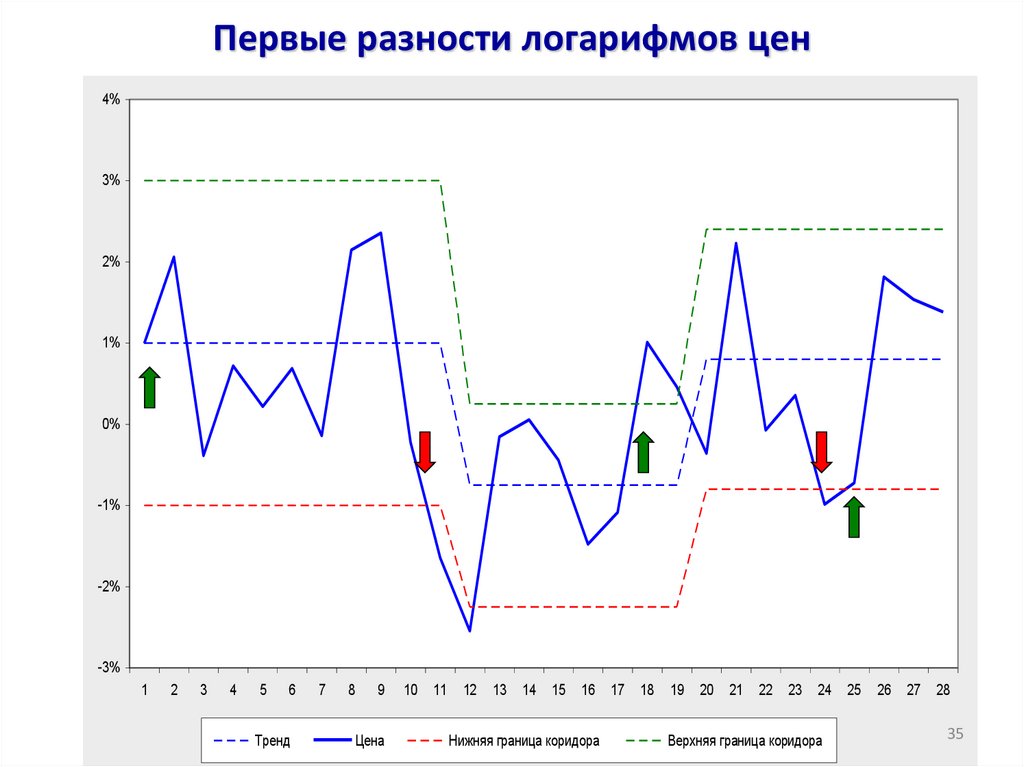
35. Первые разности логарифмов цен
4%3%
2%
1%
0%
-1%
-2%
-3%
1
2
3
4
5
6
Тренд
7
8
9
Цена
10
11
12
13
14
15
16
Нижняя граница коридора
17
18
19
20
21
22
23
24
Верхняя граница коридора
25
26
27
28
35
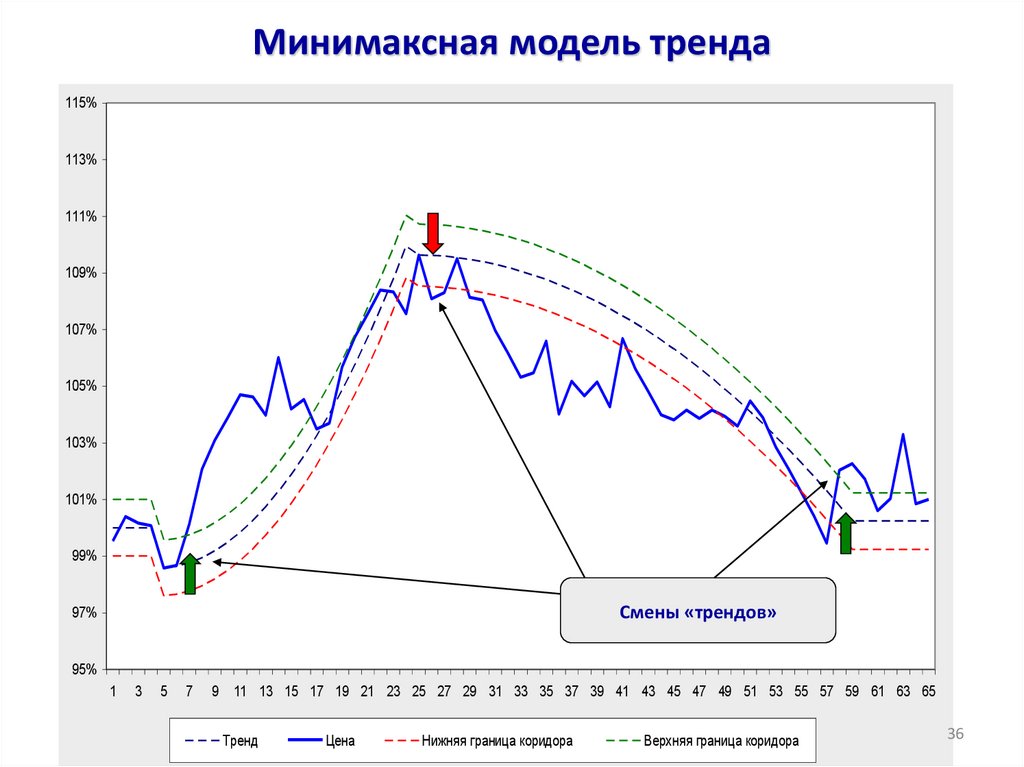
36. Минимаксная модель тренда
115%113%
111%
109%
107%
105%
103%
101%
99%
Смены «трендов»
97%
95%
1
3
5
7
9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65
Тренд
Цена
Нижняя граница коридора
Верхняя граница коридора
36
37. Пояснения к моделям
Кусочно-линейная модель1. Базовые цены Ct или (Ht+Lt)/2.
2. EAn·An-1<0, для любого n.
3. Проверяется гипотеза о знаке An
(направление тренда).
Минимаксная модель
1. Для растущего тренда базовая цена Lt и
проверяется гипотеза An>0.
2. Для падающего тренда базовая цена Ht и
проверяется гипотеза An<0.
37
38. Сильная антиперсистентность
Х1, X2,,…, - стационарная в широком смыслепоследовательность m-зависимых случайных
величин. Т. е. для любых i1<….<ik<ik+m<
j1<….<jl многомерные случайные величины
( X i1 ,..., X im ) и ( X j1 ,..., X jl )
независимы.
Cильная антиперсистентность
1. EХi=0;
m
( 0)
t 1
2
2. (t )
.
38
39. Сильная антиперсистентность
Свойстваn
m
t 1
t 1
D X i 2 i (i ) для любого n m
m
(0)
t 1
2
m
(0)
t 1
2
COV ( X i m , X i m t )
COV ( X i , X i t )
, для любого i 0
, для любого i 0
39
40. Сильно антиперсистентная модель
I- множество номеров n, таких, чтоht (Ц)=Ln Цt/Цt-1 , Тn-1<t≤Тn,
отрезок сильно антиперсистентной
последовательности с симметричным
одномерным распределением.
Сильно антиперсистентная модель (САМ)
1. Dn Dn ;
n I
n I
2. Если n I , то n 1 I и n 1 I ;
3. Dn const , для любого n I .
4. Если n I , то Eht ( Ц ) const , Tn 1 t Tn
40
41. Сильно антиперсистентная модель
Пусть последовательность разностейлогарифмов цен
X n Ln( Ц Tn / Ц Т n 1 ), n I
последовательность независимых случайных
величин, а
X n Ln( Ц Tn / Ц Т n 1 ), n I
марковская последовательность.
Тогда для любого t
E (Ln Цt)2≤const ·|I|,
где |I| - мощность множества I.
Замечание. САМ может быть УНМ.только при условии
Sn=0 для любого n из I.
41
42. Соответствие рынку
Между выборочными дисперсиями ht(С)минуток (D(1)) и 15-ти минуток (D(15)) внутри
дня (т. е. после выбрасывания из данных
приращений логарифмов цен междневных гэпов),
рассчитанными за 50 дней, значительную долю
времени (свыше 95%) выполняется соотношение
15· D(1) > D(15)
из которого следует, что в те же времена для
минуток имело место соотношение
14
CORR (hi (C ), hi t (C )) 0
t 1
42
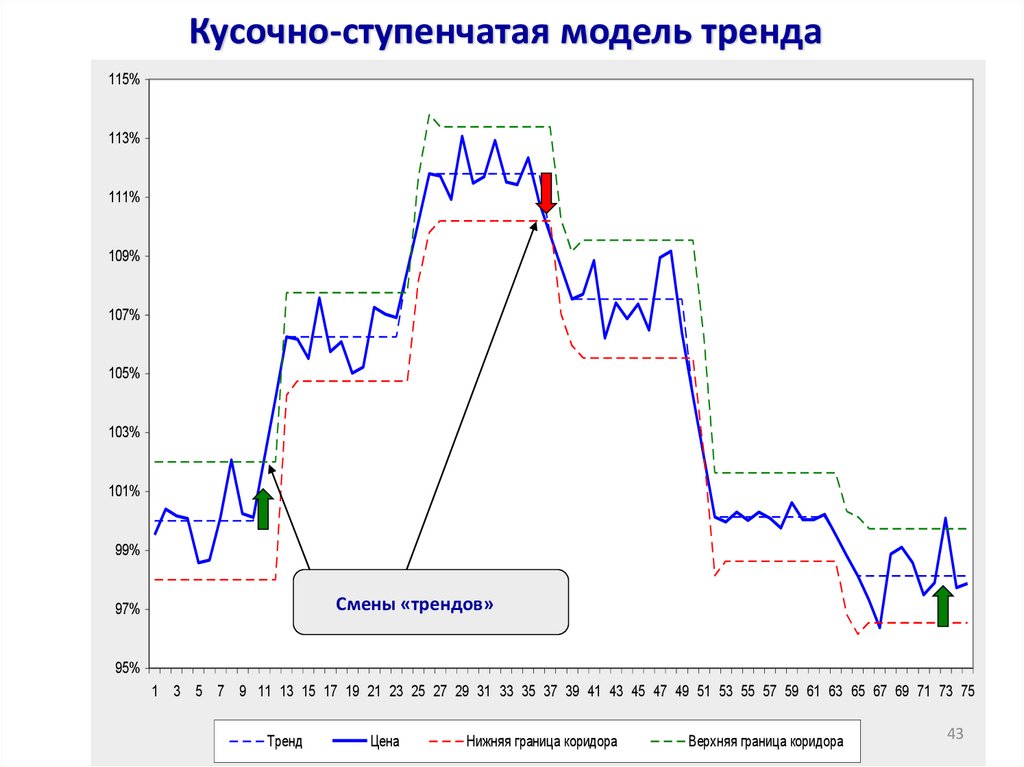
43. Кусочно-ступенчатая модель тренда
115%113%
111%
109%
107%
105%
103%
101%
99%
Смены «трендов»
97%
95%
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75
Тренд
Цена
Нижняя граница коридора
Верхняя граница коридора
43
44. Пояснения к модели
1.Базовые цены Ct или (Ht+Lt)/2.2. Если
n ,Iто
EХn·Xn-2=const=ρ.
3. Проверяется гипотеза о знаке ρ.
44
45. Соответствие рынку
1. «Тяжелые хвосты» в распределенииприращений логарифмов цен по любому
таймфрейму могут быть объяснены в рамках
любой из предложенных моделей.
2. Наличие «антиперсистентности» в
приращениях логарифмов цен минут внутри
дня может быть объяснено в рамках САМ.
3.Нулевая АКФ и отсутствие, как глобальной
(!) «антиперсистентности», так и
«персистентности», в приращениях
логарифмов цен часов внутри дня может
быть объяснено в рамках УНМ.
45
46. Соотношение САМ и УНМ
При вышеуказанных дополнительныхусловиях и |I|→∞ распределение
приращения логарифма цены в САМ
модели за весь период сходится к
нормальному распределению с
некоторым средним и дисперсией
~O(|I|).
САМ для тиков и минут и УНМ для
часов и дольше, не противоречат друг
другу.
46



































 finance
finance








