Признаки параллельности прямых (1 урок)

1. Какие из следующих утверждений неверны?

Смежные углы равны.
2) Биссектриса треугольника делит его
на 2 равные части.
3) Радиусы окружности равны
4) В равностороннем треугольнике
каждый угол равен 60°
1)
5) Высоты в треугольнике
пересекаются в одной точке

2.

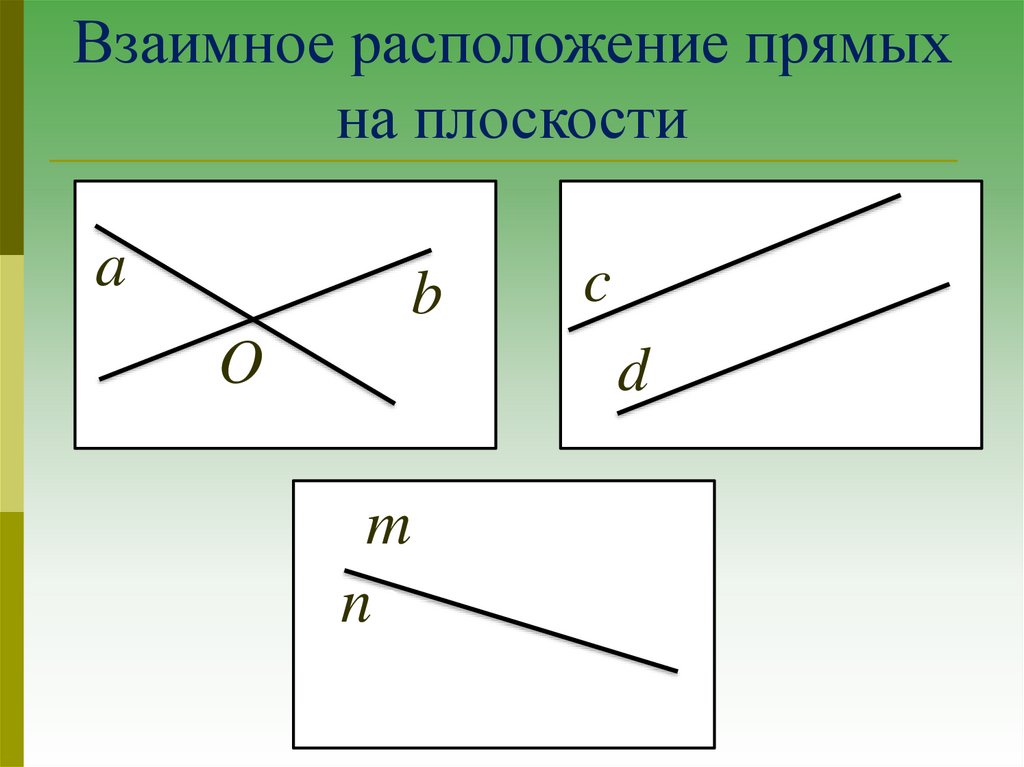
Взаимное расположение прямых
на плоскости
a
b
O
c
d
m
na

3.

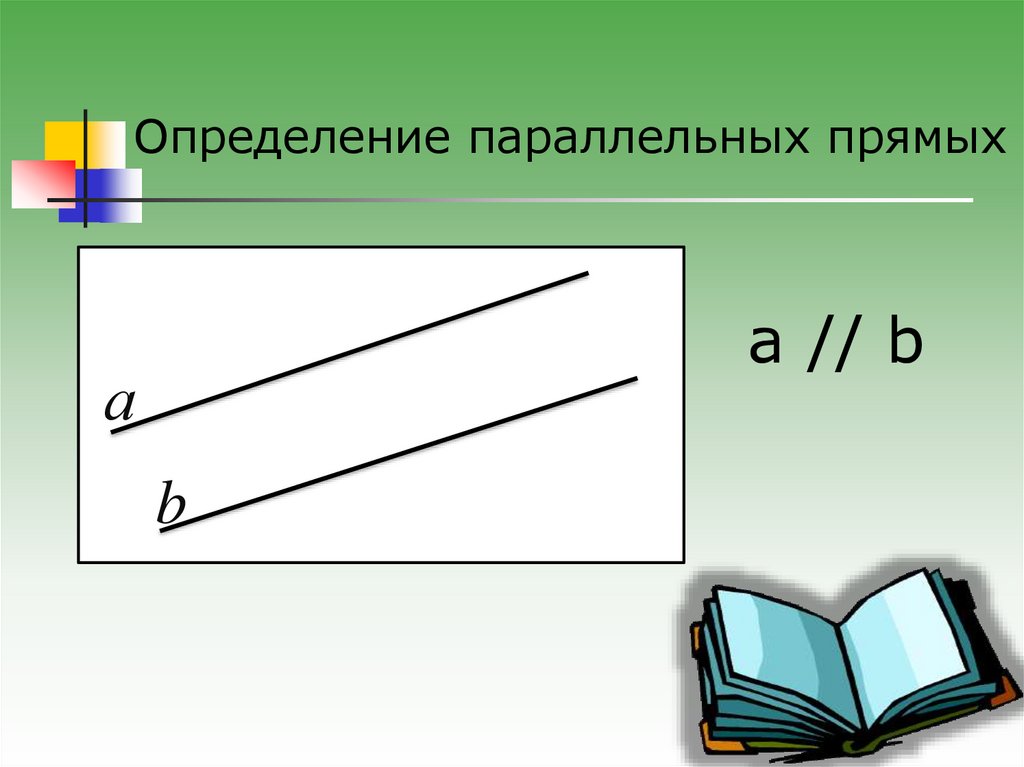
Определение параллельных прямых
a // b
а
b

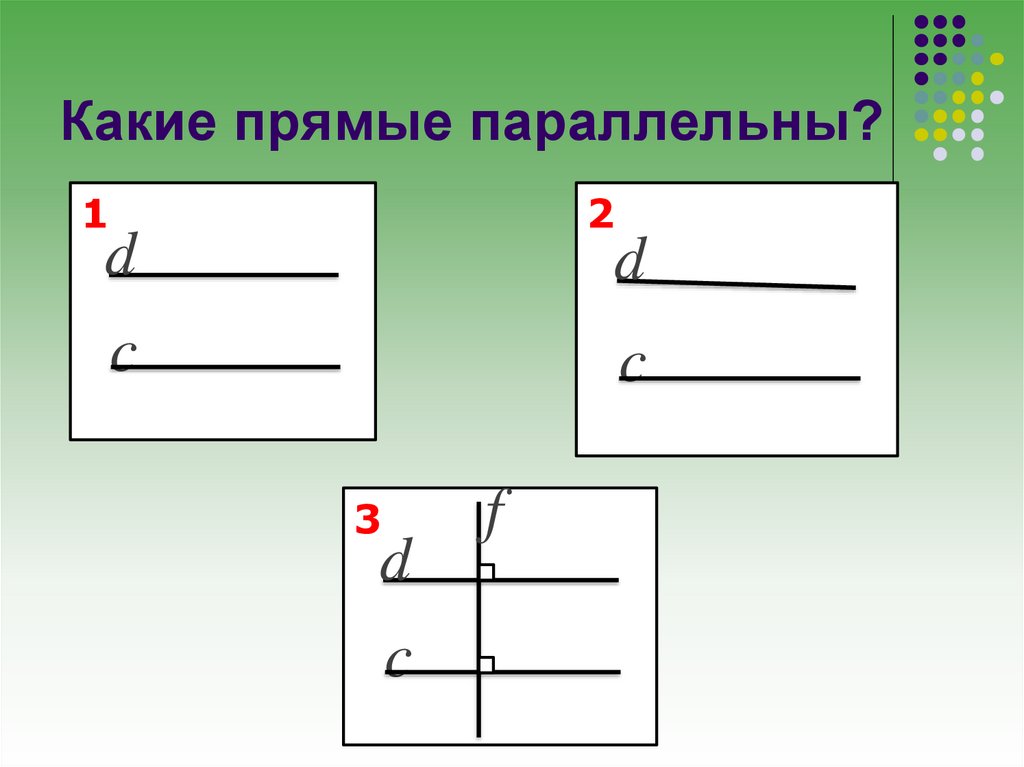
4. Какие прямые параллельны?

1
2
d
d
c
c
3
d
c
f

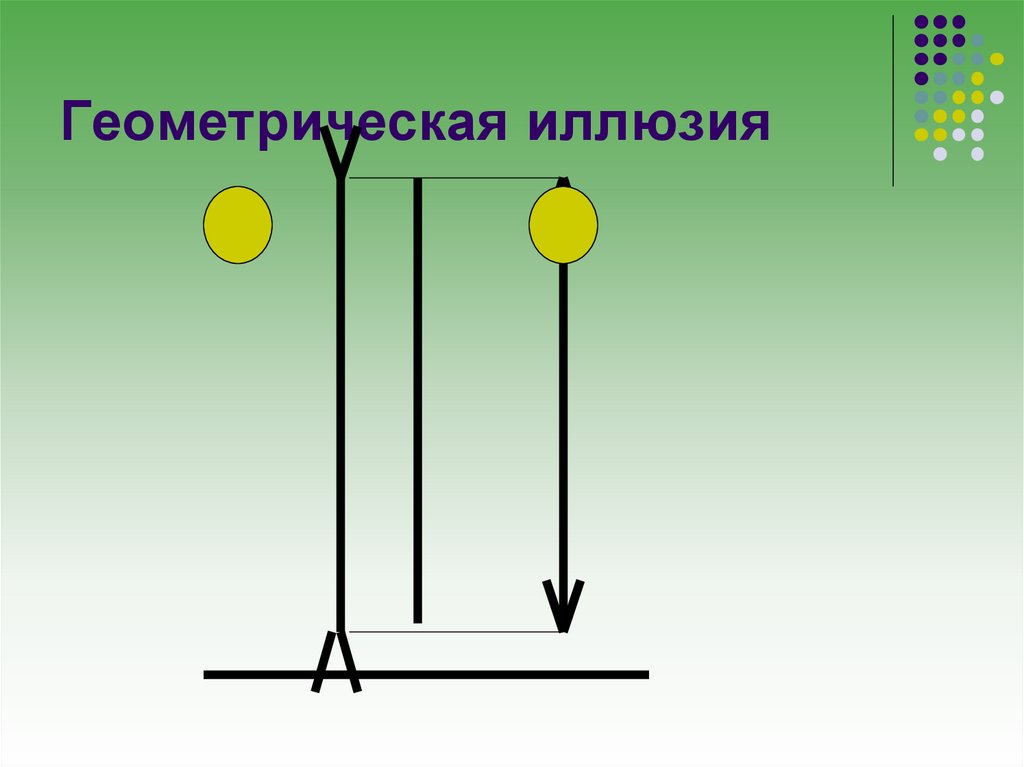
5. Геометрическая иллюзия

6. Геометрическая иллюзия

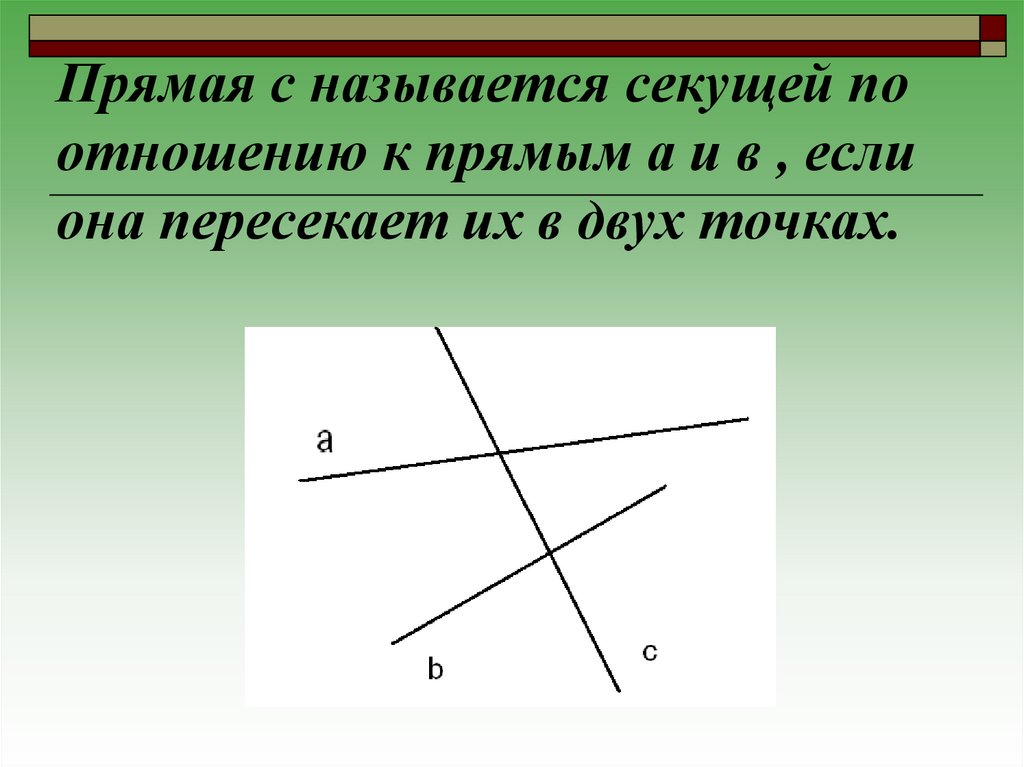
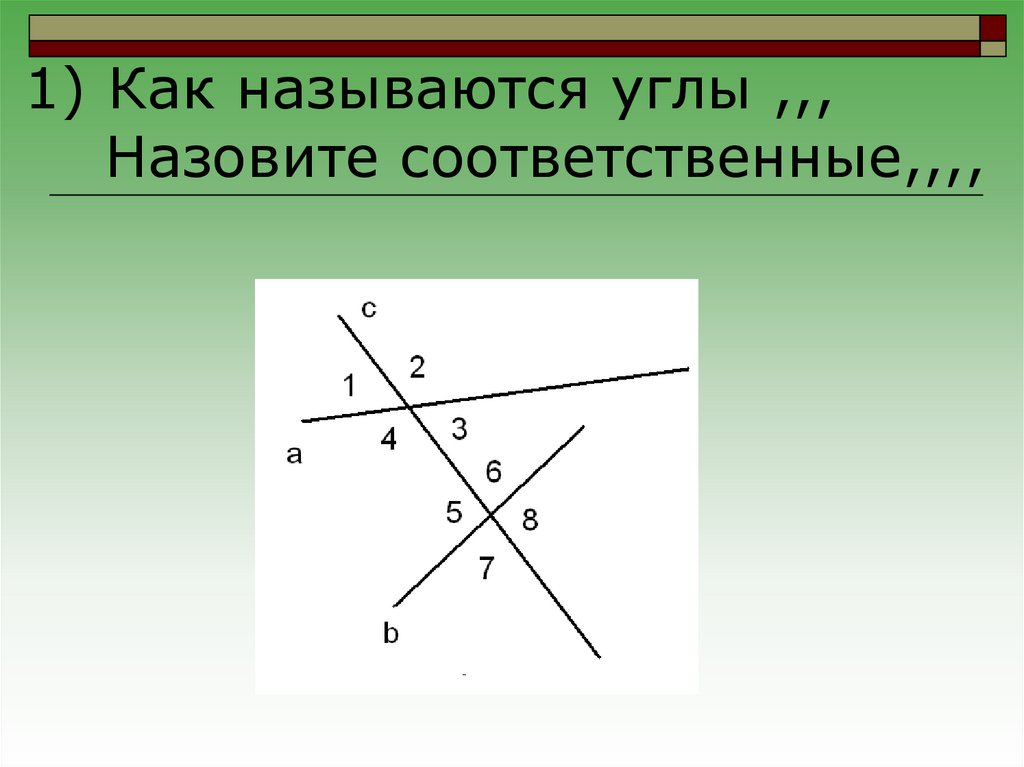
7. Прямая с называется секущей по отношению к прямым а и в , если она пересекает их в двух точках.

8.

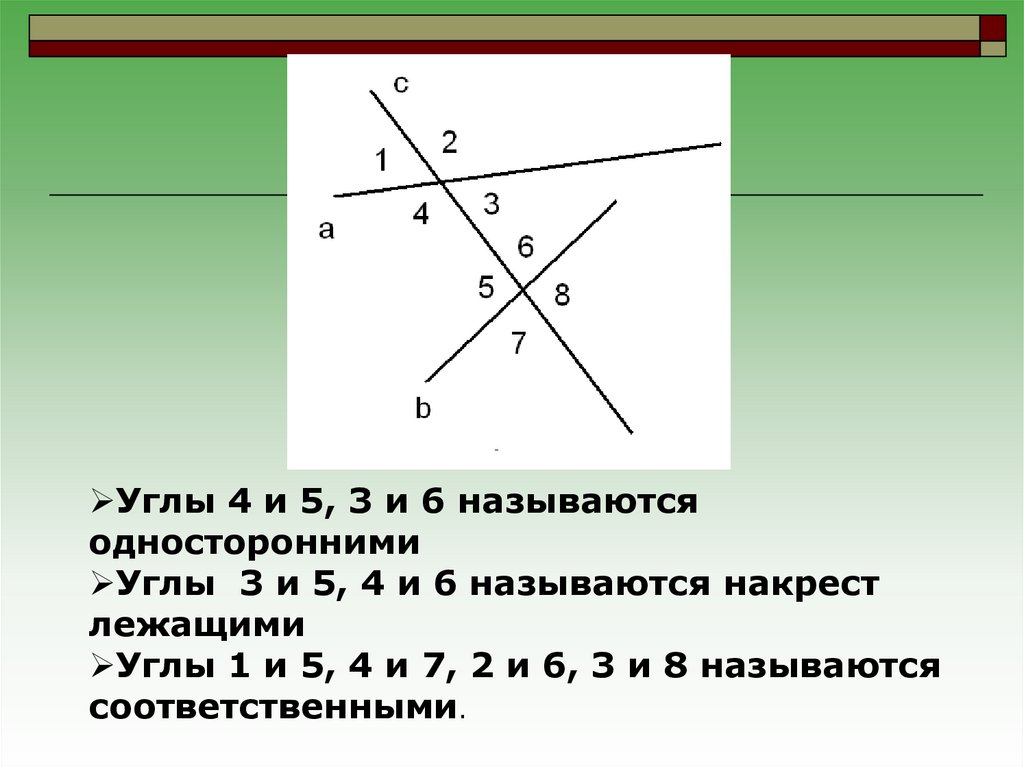
Углы 4 и 5, 3 и 6 называются
односторонними
Углы 3 и 5, 4 и 6 называются накрест
лежащими
Углы 1 и 5, 4 и 7, 2 и 6, 3 и 8 называются
соответственными.

9.

«Признаки
параллельности прямых»

10.

Признак 1.
Если при пересечении двух прямых
секущей накрест лежащие углы
равны, то прямые параллельны.
c
а и b – прямые
a
с – секущая,
1
1) 1и 2 накрест лежащие
b
2
2) 1 2
(по опр)
из 1)-2) следует а||b
(по призн. параллельности)

11.

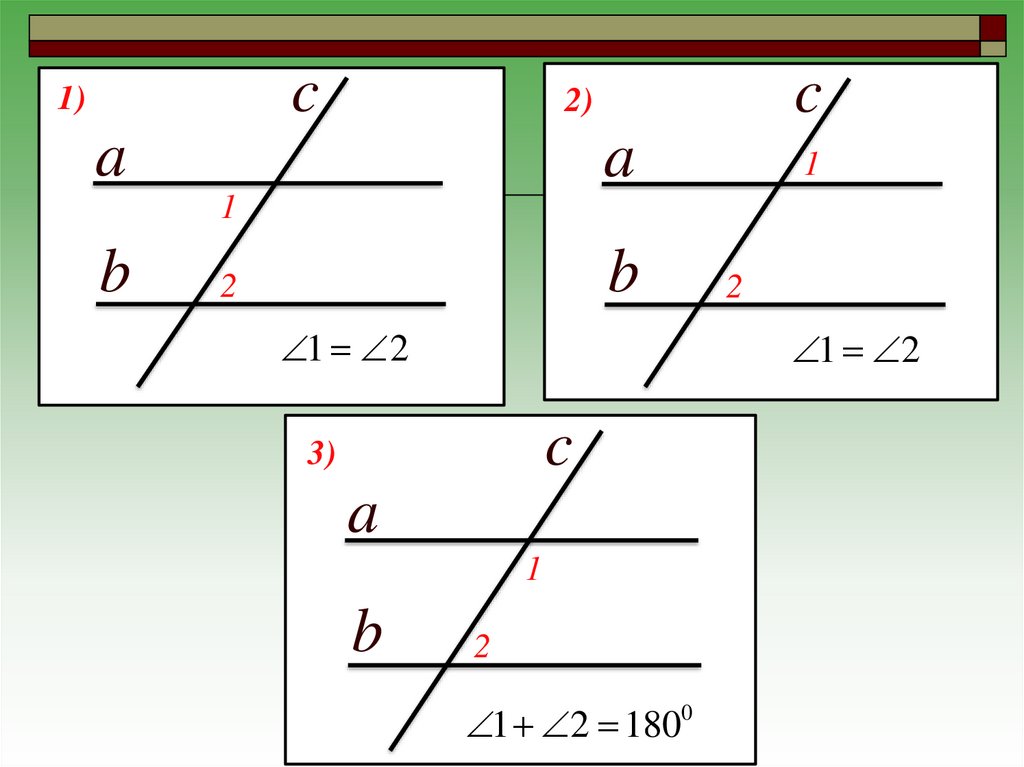
c
1)
c
2)
a
a
1
1
b
b
2
1 2
1 2
c
3)
a
1
b
2
2
1 2 1800

12. Д/З:

С. 66 в. 1-5, учить + чертеж + символьно
№ 186, 187

13.

1) Как называются углы ,,,
Назовите соответственные,,,,

14.

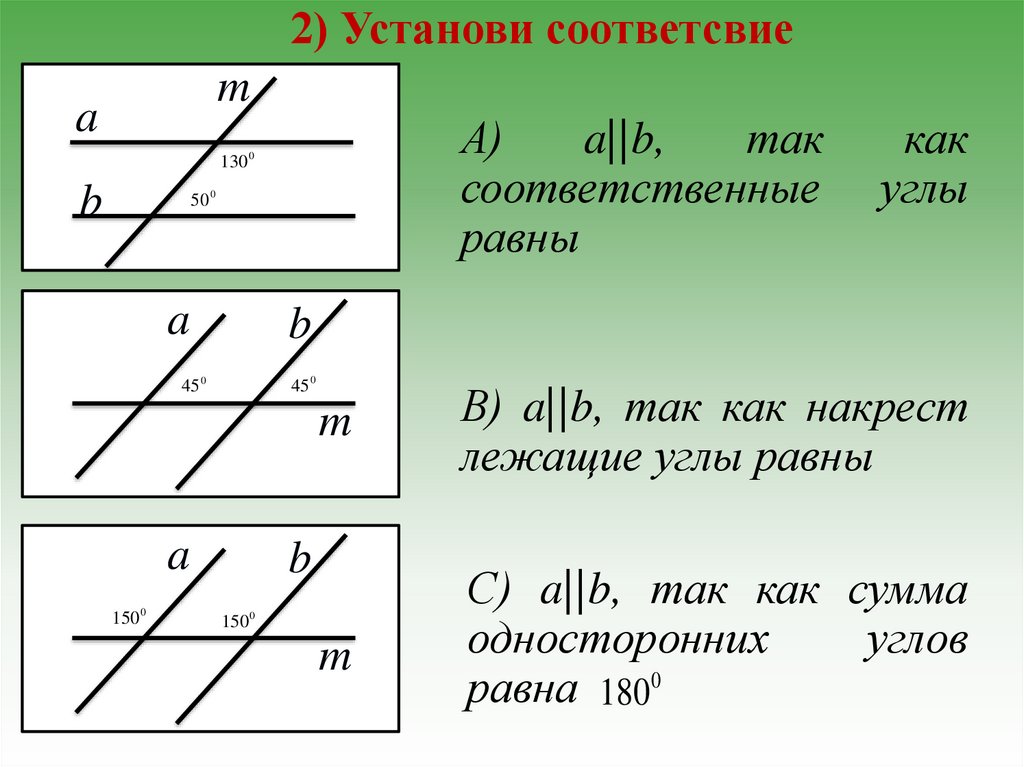
2) Установи соответсвие
m
a
А)
a||b,
так
соответственные
равны
130 0
b
50 0
a
b
45 0
45 0
a
150
0
как
углы
m
В) a||b, так как накрест
лежащие углы равны
m
С) a||b, так как сумма
односторонних
углов
равна 1800
b
150
0

15.

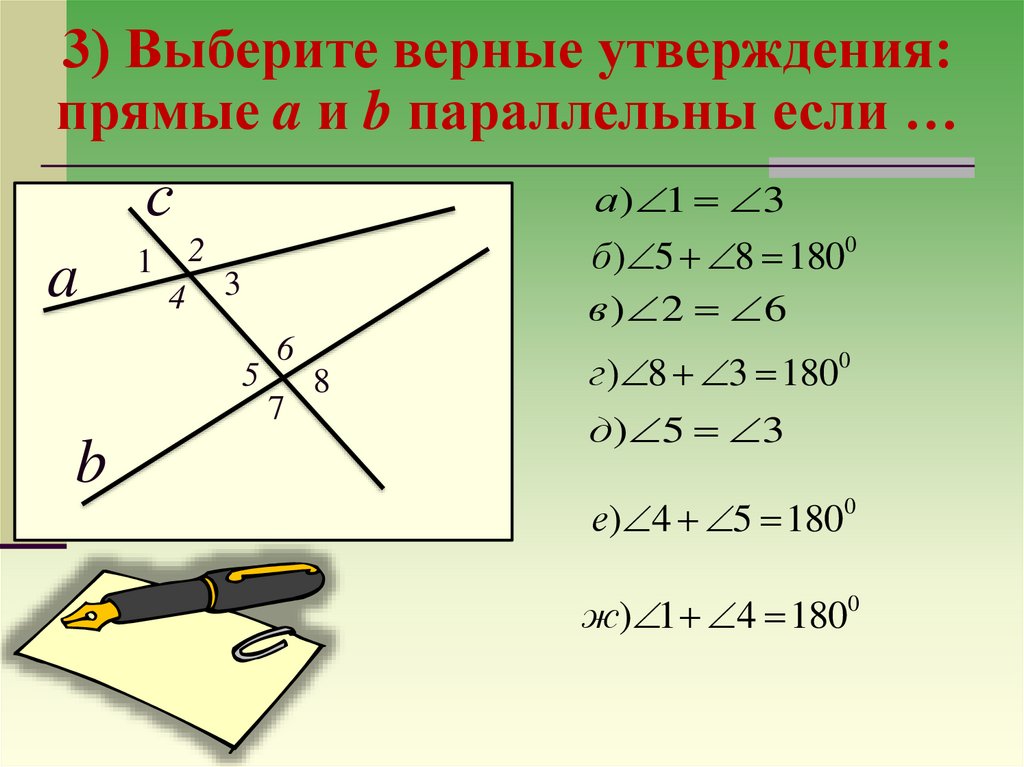
3) Выберите верные утверждения:
прямые a и b параллельны если …
с
a
а ) 1 3
б ) 5 8 1800
в ) 2 6
2
1
4
3
5
6
7
b
8
г ) 8 3 1800
д) 5 3
е) 4 5 1800
ж) 1 4 1800

16.

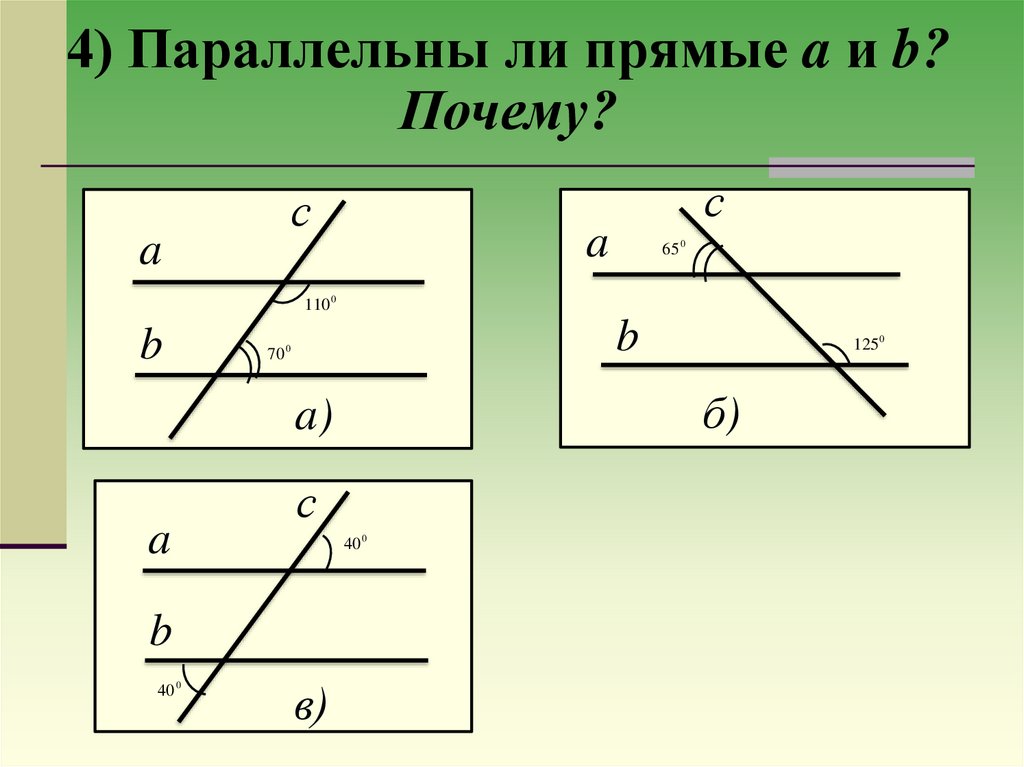
4) Параллельны ли прямые a и b?
Почему?
с
a
с
a
65 0
110 0
b
b
70 0
б)
a)
a
с
40 0
b
40 0
в)
125 0

17.

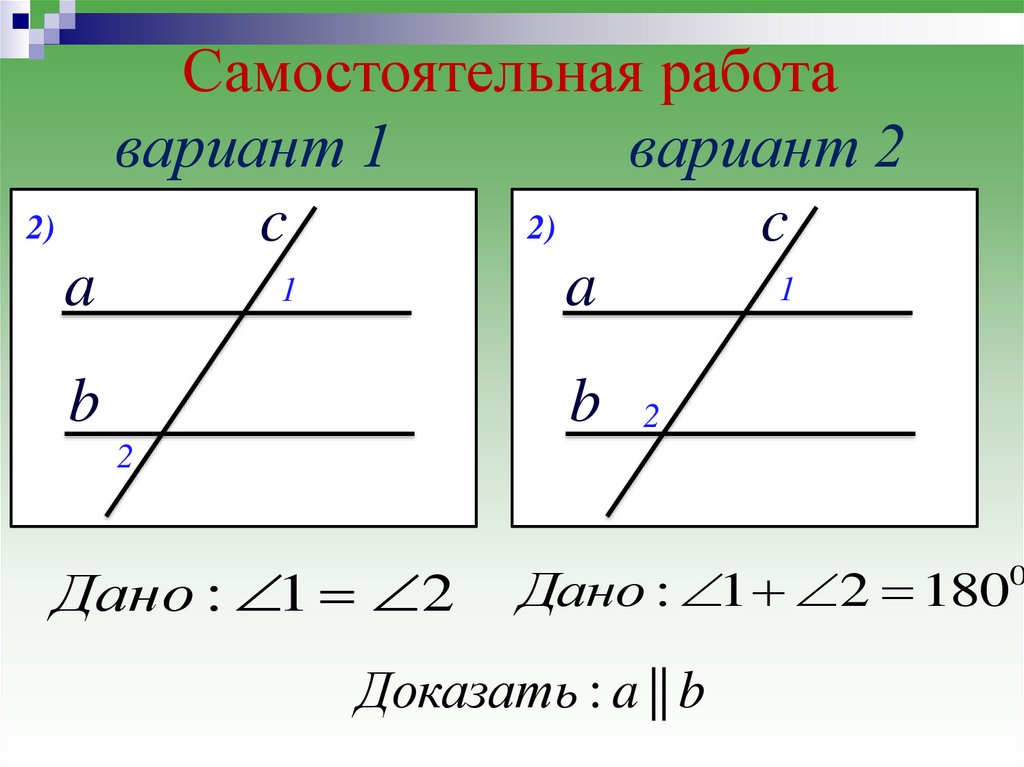
Самостоятельная работа
вариант 1
вариант 2
2)
2)
c
c
1
1
a
a
b
b 2
2
Дано : 1 2
Дано : 1 2 180
Доказать : a || b
0