Similar presentations:
Операторы и функции
1.
1. ЛАБОРАТОРНЫЕ РАБОТЫ1.1. Операторы и функции
Вариант 1
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис. 1.1).
x2 y
1
3 4.
2. Для x [–4,7; 0,2] вычислить b
y
Значение у — произвольное. Шаг изменения x равен
0,2.
3. Даны действительные положительные числа a,
b, c, d. Выяснить, можно ли прямоугольник со сторонами a, b уместить внутри прямоугольника со сторонаРис. 1.1
ми c, d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой из сторон второго
прямоугольника.
sin 3 cx 3 x 2
. Шаг изменения c ра4. Для c [–2,1; 3,2] вычислить z
3
2 2
cx x 3,14
вен 0,2. Параметр x = –1,7. Значения c и z вывести в виде таблицы. Подсчитать количество значений z, больших и меньших нуля.
5. Даны действительное число a, натуральное число n. Вычислить
a(a + 1)…(a + n – 1).
6. Вычислить
n
n
k 1
i 1
k 3 (k i)2 .
7. Дано действительное число x. Последовательность a1 , a2 , ... образована по
закону
x
an
.
n!(n 1)!
Найти первый член, для которого выполняется условие an an 1 .
8. Даны действительные x, . Вычислить с точностью до
( x)2 k
.
2k !
k 0
Вариант 2
1. Определить, принадлежит ли точка (х, у) заштрихованной части плоскости
(рис. 1.2).
4
2.
2. Для х [–2,1; 2,1] вычислить y1 1 sin x
2
. Шаг
изменения x равен 0,1.
3. Дано действительное число h, Выяснить, имеет ли
уравнение
ax 2 bx c 0
действительные корни, если
a
sin18h 17
,
(1 sin 4h) 2
b 1
3
,
3 cos ah 2 sin ah
Рис. 1.2
c ah 2 sin bh bh3 cos ah.
Если корни существуют, то найти их. В противном случае ответом должно быть
сообщение, что корней нет.
4. Для х [–2,1; 2,1] вычислить y 3 2sin x 3cos x . Шаг изменения х равен
0,1. Значения х и y вывести в виде таблицы. Найти максимальное значение y на
данном интервале.
5. Даны действительное число a, натуральное n. Вычислить
a (a n)(a 2n)...(a n 2 ) .
6. Вычислить
n
4i
i 2
5
i 0
7. Дано действительное число x. Последовательность a1 , a2 , ... образована по
x
2an 1 для
следующему закону: начальное значение a1 x , значение an
1 an 1
n = 2, 3, … Найти первый член an , для которого выполняется условие
an an 1 .
8. Даны действительные числа x, . Вычислить с точностью до
x 2 k 1
k 1
( 1)
.
2k
(
1)
x
k 1
Вариант 3
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной
части плоскости (рис. 1.3).
2. Для x [–1,7; 6,1] вычислить b xe ( x 3) . Шаг изменения x равен 0,1.
5
3.
3. Даны действительные числа a, b, c, d, s, t, u, одновременно не равные нулю. Известно, что точки (a, b)и (c, d) не лежат на прямой, заданной уравнением
sx + ty + u = 0. Прямая разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что
точки (a, b) и (c, d) принадлежат разным полуплоскостям. Примечание: две точки (a, b) и (c, d), не лежащие
на прямой sx + ty + u = 0, принадлежат одной полуплоскости, если sa + tb + u и sc + td + u — числа одного знака.
1
4. Для x [–2,7; 0,1] вычислить z
.
Рис. 1.3
(1 x 2 ) yx
Шаг изменения x равен 0,2. y = 0,7. Вывести значения x и z в виде таблицы. Определить минимальное значение z на данном интервале.
5. Дано действительное число a. Найти такое наименьшее n, что
1
1
1 ... a .
2
n
6. Вычислить
n
k!
.
5
k
k 1
7. Дано действительное число x. Последовательность a1 , a2 , ... образована по
x2
следующему закону: a1 x , an 3an 1
для n = 2, 3, … Найти первый член
4an 1
an , для которого выполняется условие an an 1 .
8. Даны действительные числа x, . Вычислить с точностью до
( 1) k 1 x3k
.
(2k )!
k 0
Вариант 4
1. Определить, принадлежит ли точка с координатами (x, y) заштрихованной
части плоскости (рис. 1.4).
3
2
y x
y x
2. Для x [0,8; 3,4] вычислить z
. Значение y произволь2
3
ное. Шаг изменения х равен 0,1.
3. Дано действительное число a. Вычислить f(a), если
0
при x 0,
f(x) x
при 0 x 1,
x3
в противном случае.
6
4.
4. Для у [–0,5; 0,5] найти z1,2 9,8 x
1 y
2
. Шаг из-
менения у равен 0,1. Параметр x = 1,7. Значения z и y
вывести в виде таблицы. Найти количество значений z,
больших и меньших нуля.
5. Дано натуральное число n. Вычислить
n
2i
.
i 1 (i 1)!
6. Вычислить
Рис. 1.4
n
1
.
2
k 1 (2k )
7. Дано действительное число x. Последовательность a1 , a2 , ... образована по
1
закону: a1 x , an 3 n sin(an 1 x) для n = 2, 3, … Найти первый член an , для
3
которого выполняется условие an an 1 .
8. Даны действительные числа x, . Вычислить с точностью до
( 1) k x 2 k 1
.
k 0 k !( k 1)!
Вариант 5
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис.
1.5).
x y
2. Для x [–1,7; 1,7] вычислить a (1 x) 2
.
x 4
Значение y произвольное. Шаг изменения x равен 0,2.
3. Дано действительное число a. Вычислить f(a),
если
x2 4 x 5
при x 2,
f (x)
1
в противном случае.
2
Рис. 1.5
x 4x 5
sin( x cos x)
4. Для x [–3,7; 3,7] вычислить y sin 2 x
. Шаг изменения x
5,1
равен 0,2. Значения x и y вывести в виде таблицы. Найти количество значений y,
больших и меньших нуля.
5. Дано натуральное n. Вычислить
7
5.
n1
k!
1
1
k 1
k 1
2 3
.
6. Вычислить
1·2 + 2·3·4 + … + n(n + 1)…2n.
7. Дано действительное число a. Последовательность x1 , x2 , ... образована по
1
следующему закону: x1 a, x n n xn 1 для n = 2, 3, … Найти первое xn для кото2
рого выполняется условие xn xn 1 .
8. Даны действительные числа x, . Вычислить с точностью до
( 1) k x 2( k 1)
.
(k !) 2
k 0
Вариант 6
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис.
1.6).
x2 y2
1
2
4 .
2. Для x [–2,5; 2,5] вычислить a
x 1
Значение у произвольное. Шаг изменения x равен 0,2.
3. Дано действительное число a. Вычислить f(a),
если
при x 0,
0
2
при 0 x 1,
f ( x) x x
x 2 sin x 2
в остальных случаях.
Рис. 1.6
12, 4 x 0,6e x
. Шаг изменения x равен
4. Для x [–3,1; 3,1] вычислить y
3
0,2. Значения x и y вывести в виде таблицы. Найти минимальное значение y на
данном интервале.
5. Даны целые числа n, k ( n k 0 ). Вычислить
n(n 1)...(n k 1)
.
k!
6. Вычислить
n
( 1) k 1 n
,
k 1 k ( k 1)
где k, n — целые.
7. Даны действительные числа a, b. Последовательность y1 , y2 , ... образова8
6.
на по закону y1 a, y 2 b, y n y n 1 y n 2 для n = 3, 4, … Найти первое значение yn , для которого выполняется условие yn yn 1 .8. Даны действительные числа x, . Вычислить с точностью до
( 1) k x 4 k
.
k 0 (2k )!(4k 1)
Вариант 7
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис. 1.7).
2. Для
y [–2,5; 2,5]
вычислить
2
( y x)
b 1 y x
. Значение х произвольное. Шаг
2
изменения y равен 0,1.
3. Даны действительные числа a, b, c ( a 0 ). Полностью исследовать уравнение ax4 + bx2 + c = 0. Если
действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выведены два или
четыре корня.
Рис. 1.7
2
cos x
4. Для x [–5,7; 5,7] вычислить y tgx
.
3
2
x x
Шаг изменения x равен 0,5. Значения x и y вывести в виде таблицы. Найти минимальное значение у на данном интервале.
5. Даны действительное число a, натуральное n. Вычислить
1
1
1
...
a a (a 1)
a (a 1)...(a n)
6. Вычислить
n
xk
2k
k 1 2
7. Даны действительные числа a, b. Последовательность x1 , x2 , ... образована
по закону xn a b cos(0,5n) . Найти первое xn , удовлетворяющее условию
xn xn 1 .
8. Даны действительные числа x, . Вычислить с точностью до
( 1) k x 4 k
k 0 ( k 1)!(4k 1)
Вариант 8
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной
части плоскости (рис. 1.8).
9
7.
2. Дляx [–3,2; 3,4]
вычислить
2
3
x
x
a x Шаг изменения x равен 0,2.
2 3
3. Даны три действительных числа. Возвести
в квадрат те из них, значения которых неотрицательны.
4. Для
x [–4,2; 4,2]
вычислить
y sin(3tgx x ) . Шаг изменения x равен 0,2.
Значения x и y вывести в виде таблицы. Найти
максимальное значение y на данном интервале.
5. Дано действительное число a. Найти среРис. 1.8
ди чисел
1
1 1
1, 1 , 1 , ...
2
2 3
первое, большее a.
6. Вычислить
1 1
1
1
1
2 3
9999 10000
7. Даны действительные числа a, b. Последовательность x1 , x2 , ... образована
по закону xn 0,5a b sin(0,5n) . Найти первое xn для которого выполняется условие xn xn 1 .
8. Даны действительные числа x, . Вычислить с точностью до
( 1) k x 2 k 1
k
!(2
k
1)
k 0
Вариант 9
1. Определить, принадлежит ли точка с координатами
(х, у) заштрихованной части плоскости (рис. 1.9).
3 sin y
. Зна2. Для y [–5,6; 1,8] вычислить a
1 x 2 y tgy
чение x произвольное. Шаг изменения y равен 0,2.
3. Даны действительные числа a, b, c ( a 0 ). Выяснить, имеет ли уравнение ax2 + bx + c = 0 действительные
корни. Если такие корни имеются, то необходимо найти их.
В противном случае ответом должно служить сообщение,
что действительных корней нет.
Рис. 1.9
5,1x 2
. Шаг изменения x равен 0,2.
x4
Значения x и y вывести в виде таблицы. Найти минимальное значение y на данном
4. Для x [–1,7; 1,7] вычислить y tg 2 x
10
8.
интервале.5. Дано натуральное n. Вычислить
3 6 ... 3(n 1) 3n .
6. Вычислить
( 1) k x k
k
k
(2
1)
k 1
7. Пусть
x1 = 0,5,
y1 = 0,5,
xi = 3,7yi–1,
yi = xi–1 + yi–1
i = 2, 3, … Дано натуральное n ( n 2) . Найти значения xn, yn.
8. Даны действительные x, . Вычислить с точностью до
1
x k2
k 1
n
для
Вариант 10
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис. 1.10).
2. Для
x [–3,5; 0,1]
вычислить
x2
y sin ( x x )( x ) . Шаг изменения x равен 0,1.
3
4
3. Даны действительные числа x, y, z. Получить
max(x, y, z).
x 2 sin x
. Шаг
4. Для x [–2,2; 2,2] вычислить y
Рис. 1.10
4cos x
изменения x равен 0,2.
Значения x и y вывести в виде таблицы. Найти количество значений y, больших и
меньших нуля.
1
5. Дано положительное число a. Найти наибольшее число вида n , меньшее
2
a, если n ≥ 0.
6. Вычислить
n
( 1) k (k 1)
.
k!
k 1
7. Пусть a1= b1 = 1, ak = bk–1 + 3ak–1, bk = 3bk–1 – ak–1, k = 2, 3, … Дано натуральное n ( n 2 ). Вычислить an, bn.
8. Даны действительные x, . Вычислить с точностью до
1
.
2
2
k 1 k x
11
9.
Вариант 111. Определить, принадлежит ли точка с
координатами (х, у) заштрихованной части
плоскости (рис. 1.11).
2. Для
x [–2,5; 0,5]
вычислить
2
1 cos ( x y )
. Значение y произвольное.
z
2 x sin x
Шаг изменения x равен 0,1.
3. Даны действительные числа a, b, c.
Удвоить эти числа, если a b c ; заменить их
абсолютными значениями, если это не так.
4. Для
x [–0,5; 0,5]
вычислить
Рис. 1.11
2
x
y cos( x 2 ) . Шаг изменения x равен 0,1.
4
Значения x и y вывести в виде таблицы. Определить максимальное значение y на
этом интервале.
5. Даны вещественные x, (0< <1). Вычислить
cos 2 x cos 4 x
cos 2nx
...
...
1 3
3 5
(2n 1)(2n 1)
Вычисления закончить, когда очередное слагаемое по модулю станет меньше .
6. Вычислить
( 1) k
.
2
k
k
(
1)!
k 1
7. Пусть a1 = u, b1 = v, ak = 2bk–1 + 2u, bk = 2ak–12 + 3v, k = 2, 3, … Даны действительные числа u и v, натуральное число n. Найти an, bn.
8. Даны действительные x, . Вычислить с точностью до
( 1) k x k
k
k 1
Вариант 12
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной
части плоскости (рис. 1.12).
1 cos( x 2 y )
2. Для x [–3,2; 3,2] вычислить z
. Значение y произвольное.
1 x2 y2
Шаг изменения x равен 0,1.
3. Даны действительные числа x, y, z. Получить max(x, y, z) и min(x, y, z).
12
10.
14. Для x [–1,2; 1,5] вычислить y cos(tg x 2 ) .
4
Шаг изменения x равен 0,1. Значения x и y вывести в
виде таблицы. Найти минимальное значение y на данном интервале.
5. Даны вещественные x и (0< <1). Вычислить
x 2 x3
x ... ,
2
3
если x 1 .
Вычисления закончить, когда очередное слагаемое по
Рис. 1.12
модулю станет меньше .
6. Вычислить
n
1
x .
i 1 i !
7. Пусть x1 = x2 = 1, xi = xi–1 + xi–2, i = 3, 4, … Дано натуральное n ( n 3 ). Найти xn.
8. Даны действительные x, . Вычислить с точностью до
x2
.
3
k 1
k2
Вариант 13
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис.
1.13).
y
2
2. Для x [–3,2; 3,2] вычислить z x 4 .
1
1 2
x 4
Рис. 1.13
Значение у произвольное. Шаг изменения x равен 0,1.
3. Даны действительные числа x, y. Вычислить
если x y,
x y,
z
если x y.
y x 1,
Шаг изменения x равен 0,1. Значения x и у вывести в виде таблицы. Подсчитать
количество значений y, больших и меньших 0.
4. Для x [–1, 1] вычислить y sin (x
x
x )(x
) . Шаг изменения x
x2
x
4
равен 0,1. Значения x и y вывести в виде таблицы. Подсчитать количество значе2
13
11.
ний y, больших и меньших 0.5. Дано положительное a. Найти наименьшее число вида
1
, n 0 , большее
3n
a. (Предполагается, что a < 1.)
6. Вычислить
x cos(ix)
.
i
2
i 1
7. Даны положительные действительные числа a, x, . Последовательность
x
y1 , y2 , ... образована по закону y0 a, yi yi 1
для i = 1, 2, … Найти первый
yi 1
член последовательности yn , для которого выполняется условие yn yn 1 .
8. Даны действительны числа x, . Вычислить с точностью до
1
.
3 2
x
k
k 1
n
Вариант 14
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис. 1.14).
1 cos( x 2)
.
2. Для x [3,2; 6,7] вычислить b
x4
sin x
2
Шаг изменения x равен 0,2.
3. Даны три действительных числа. Выбрать из
них те, которые принадлежат интервалу (1, 3).
4. Для x [–2,7; 3,1] вычислить y = tg2x – zx, если
z = 0,2. Шаг изменения x равен 0,2. Значения x и y выРис. 1.14
вести в виде таблицы. Найти минимальное значение y на
данном интервале,
5. Даны вещественные x, ε (0< ε <1). Вычислить
x 1 ( x 1)3
( x 1)5
z 2[
...] .
x 1 3( x 1)3 5( x 1)5
Вычисления закончить, когда очередное слагаемое по модулю станет меньше .
6. Вычислить
n
sin kx
(1
).
k
k 1
2 xk 1
, k = 2, 3, … Найти первый член xn, для которого
7. Пусть x0 1, xk
3
выполняется условие xn xn 1 .
8. Даны действительные числа x, . Вычислить с точностью до
14
12.
xk .
k 1
3
Вариант 15
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис. 1.15).
x
2. Для x [–3,4; 0,2] вычислить z y
.
2
x
x2
y 3
Значение y — произвольное. Шаг изменения x равен 0,1.
3. Даны действительные числа x, y ( x y ). Меньшее из этих чисел заменить их полусуммой, а большее —
их удвоенным произведением.
Рис. 1.15
8,15 x3
. Шаг изменения x равен 0,4.
1 ln x
Значения x и y вывести в виде таблицы. Определить минимальное значение y на
данном интервале.
5. Даны вещественные x, (0< <1). Вычислить
1 1 1
1 ...
2 3 4
Вычисления закончить, когда очередное слагаемое по модулю станет меньше .
Полученный результат сравнить с точным значением суммы 0,6931478…
6. Вычислить
n
1
(2 ).
i!
i 1
b
7. Пусть b0 1, bi bi 1 ii 11 , i = 1, 2, … Найти произведение
3
b0 b1 ... bn ,
где n — натуральное число ( n 1 ).
8. Дано действительное . Вычислить с точностью до
( 2)i
.
i!
i 0
4. Для x [–5,0; 5,0] вычислить y
Вариант 16
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной
части плоскости (рис. 1.16).
15
13.
x32. Для x [–5,6; 0] вычислить b 1
. Шаг изx5
3
5
менения x равен 0,1.
3. Дано действительное число a. Вычислить f(a), если
x2
при 2 x 2,
f ( x)
в противном случае.
4
4. Для x [–0,7; 0,7] вычислить y = x·cos(2x). Шаг
Рис. 1.16
изменения x равен 0,1. Значения x и y вывести в виде таблицы. Найти количество значений y, больших и меньших нуля.
5. Даны вещественные x, (0< <1). Вычислить
1 1 1
1 ...
3 5 7
Вычисления закончить, когда очередное слагаемое по модулю станет меньше .
Полученный результат сравнить с точным значением суммы
6. Вычислить
4
.
( 1) k (k 1)
k!
k 0
7. Пусть a1 = u, b1 = v, ak = 2bk–1 + ak–1, bk = 2ak–12 + bk–1, k = 2, 3, … Даны действительные u, v, натуральное n . Найти an, bn.
8. Даны действительные числа m, x, (0< <1). Вычислить
mx
m(m 1) 2 m(m 1)(m 2) 3
1
x
x ...
(m 1)! (m 2)!
(m 3)!
Вычисления закончить, когда очередное слагаемое по модулю станет меньше .
n
Вариант 17
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис.
1.17).
2cos(a )
6 .
2. Для a [–0,8; 6,8] вычислить z
1
sin 2 a
6
Шаг изменения a равен 0,1.
3. Даны действительные числа x, y, z. Получить
max(x + y, z, xyz).
Рис. 1.17
4. Для
x [–1,2; 1,2]
вычислить
y 0,5 2 x 1 ( x 2)3 . Шаг изменения x равен 0,1. Значения x и y вывести в виде
16
14.
таблицы. Найти максимальное значение y на данном интервале.1
1
1
5. Даны вещественные x, ε (0< ε <1). Вычислить
... Вычис1 2 2 3 3 4
ления закончить, когда очередное слагаемое по модулю станет меньше . Полученный результат сравнить с точным значением суммы — 1.
6. Вычислить
n
i!
.
2
i 1 i 2i 3
u u v v
u v
7. Пусть u1 u2 0, v1 v2 1, ui i 1 i 22 i 1 2 i 2 , vi i 1 i 1 ,
ui 2 vi 1
1 ui 1 vi 1
i = 3, 4, … Дано натуральное n ( n 3 ). Получить vn, un.
8. Даны действительные числа x, ( x 0, 0) . Вычислить с точностью до
( 1) k x 2 k 1
.
k
k
!(2
1)
k 0
Вариант 18
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис. 1.18).
x
e 7,8sin 3 x 2
2. Для x [9,1; 15,6] вычислить y
.
1
1
x x
2
3
Шаг изменения x равен 0,2.
3. Даны два действительных числа. Заменить первое из них нулем, если оно меньше или равно второму,
и оставить числа без изменения в противном случае.
1
4. Для x [–0,7; 0,7] вычислить y sin x 2 cos x .
Рис. 1.18
2
Шаг изменения x равен 0,2. Значения x и y вывести в виде таблицы. Найти минимальное значение y на данном интервале.
5. Даны вещественные x, ε (0< ε <1). Вычислить
x3 x5
x ... ( x 1).
3 5
Вычисления закончить, когда очередное слагаемое по модулю станет меньше .
6. Вычислить
n
1
i
(2
).
i!
i 1
7. Пусть a1 = b1 = 1, ak = 3bk–1 + 2ak–1, bk = bk–1 + 2ak–1, k = 2, 3, … Дано натуральное n. Вычислить an, bn.
8. Дано действительное a. Последовательность x0, x1, … образована по зако17
15.
нуmin(2a; 0,95)
a
x0
5
a
25
a
4
xn xn 1 4
5
5 xn 1
для n = 1, 2, … Дано n. Найти xn.
при a 1,
при 1 a 25,
в остальных случаях,
Вариант 19
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости (рис. 1.19).
2sin (x π)
2. Для x [9,1; 15,6] вычислить z
.
1
2
cos x
3
Шаг изменения x равен 0,2.
3. Даны действительные числа x, y. Получить
max(x, y) и min(x, y).
4. Для x [–0,8; 0,8] вычислить y sin x cos x .
Шаг изменения x равен 0,2. Значения x и у вывести в
Рис. 1.19
виде таблицы. Подсчитать количество значений y,
больших и меньших нуля, на этом интервале.
5. Даны вещественные x, ε (0< ε <1). Вычислить
1
1
1
...
1 3 2 4 3 5
Вычисления закончить, когда очередное слагаемое по модулю станет меньше .
3
Полученный результат сравнить с точным значением суммы — .
4
6. Вычислить
n
x cos(kx)
.
k
2
k 1
7. Пусть a1 = b1 = 1, ak = 3bk–1 + 2ak–1, bk = bk–1 + 2ak–1, k =2, 3, … Дано натуральное n. Найти
n
2k
2
2
a
b
1
k 1
k
k
8. Даны действительные числа x, ( x 0, 0) . Вычислить с точностью до
сумму
18
16.
( 1) k x 4 kk 0 (2k )!(4k 1)
Вариант 20
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной части плоскости
(рис. 1.20).
2. Для
x [–7,2; 5,6]
вычислить
2
1 sin ( x y )
z
. Значение y — произвольное. Шаг
2 x 2x2
изменения x равен 0,4.
3. Даны действительные числа a, b, c. Проверить, выполняются ли неравенства a < b < c.
4. Для x [–1,6; 1,6] вычислить y tg 2 x 2 x .
Рис. 1.20
Шаг изменения x равен 0,2. Значения x и у вывести в
виде таблицы. Найти минимальное значение y на данном интервале.
5. Даны вещественные x, (0 < < 1). Вычислить
1 1 1
1 ...
3 5 7
Вычисления закончить, когда очередное слагаемое по модулю станет меньше .
Полученный результат сравнить с точным значением суммы —
6. Вычислить
4
.
3k 2
k
!(1
k
)!
k 1
7. Пусть x0 = c, x1 = d, xk = q·xk–1 + r·xk–2 + b, k = 2, 3, … Даны действительные
q, r, b, c, d, натуральное n. Получить xn.
8. Даны действительные числа x, ( x 0, 0) . Вычислить с точностью до
n
( 1) k x k 2
k 0 (k 1)(k 2)!
Вариант 21
1. Определить, принадлежит ли точка с координатами (х, у) заштрихованной
части плоскости (рис. 1.21).
2. Для x [–5,5; 1,2] вычислить b cos 2 (sin x 2 ) . Шаг изменения x равен 0,1.
3. Даны действительные числа x, y, z. Вычислить
19
17.
zmin 2 ( x y , x, xyz ) 1.
2
1
.
5 x 3cos x
Шаг изменения x равен 0,1. Значения x и y вывести в
виде таблицы. Определить максимальное значение y на
данном интервале.
5. Дано натуральное n. Вычислить
y
4. Для x [–0,5; 1,5] вычислить
2 2 ... 2 ,
где количество корней n.
6. Вычислить
Рис. 1.21
n
n
k 1
m k
x k
m
7. Дано действительное число x. Последовательность a1 , a2 , ... образована по
x n cos( x n 1 )
закону an
. Найти первый член, для которого an an 1 .
n2
8. Даны действительные числа x, . Вычислить с точностью до
( 1) k (k 1) x k
.
3k
k 0
9. Дано действительное a. Среди чисел
1
1 1
1, 1 2 , 1 2 2 , ...
2
2 3
найти первое, большее a (a < 2).
Вариант 22
1. Определить, принадлежит ли точка с
координатами (х, у) заштрихованной части
плоскости (рис. 1.22).
2. Для
y [–2,1; 2,1]
вычислить
y
z sin( y x )( y
) . Значение x произ2
x
x3
4
вольное. Шаг изменения y равен 0,1.
3. Даны действительные числа x, y. Если x
и y отрицательны, то каждое значение заменить
Рис. 1.22
его модулем; если отрицательно только одно из
них, то оба значения увеличить на 0,5; если оба значения неотрицательны и ни
одно из них не принадлежит отрезку [0,5; 2,0], то значения уменьшить в 10 раз; в
остальных случаях x и y оставить без изменения.
20
18.
cos xsin x
. Шаг изменения x равен
4 11 3 7
0,2. Значения x и y вывести в виде таблицы. Найти минимальное значение y на
данном интервале.
5. Дано натуральное n, действительное x. Вычислить
sin x sin sin x ... sin sin ...sin x (n раз).
6. Вычислить
n
(1 x) k 1
k 1 ( k 1)! 1
7. Дано действительное число x. Последовательность a1 , a2 , ... образована по
n!
закону an n . Найти первый член an , для которого выполняется условие
x
an an 1 .
8. Даны действительные числа x, . Вычислить с точностью до
( 1) k x k 1
3
k 1 ( k 1)
4. Для x [–2,1; 2,1] вычислить y
Вариант 23
1. Определить, принадлежит ли точка с
координатами (x, y) заштрихованной части
плоскости (рис. 1.23).
2. Для
х [–1,9; 1,9]
вычислить
2
x x
y
. Шаг изменения x равен
1 sin 2 ( x 0,5)
0,1.
3. Даны действительные положительные
числа a, b, c, x, y. Выяснить, пройдет ли кирпич
с ребрами a, b, c в прямоугольное отверстие со
Рис. 1.23
сторонами x, y. Просовывать кирпич разрешается только так, чтобы каждое из ребер было параллельно или перпендикулярно
каждой из сторон отверстия.
4. Для х [–3,5; 3,5] вычислить y
cos x sin 3 x . Шаг изменения x равен
6
0,2. Значения x и y вывести в виде таблицы. Найти минимальное значение у на
данном интервале.
5. Дано натуральное число n. Вычислить
1
1
1
(1 2 ) (1 2 ) ... (1 2 ) .
1
2
n
6. Вычислить
21
19.
nk
( k 1 cos x ) .
k
k 1
yk 1 1
, k = 1, 2, … Дано действительное 0< <1. Найти
yk 1 2
первый член yn , для которого выполняется yn yn 1 .
8. Даны действительные числа x, . Вычислить с точностью до
( 1) k 1 x k
( ).
k
(
1)!
3
k 1
7. Пусть y0 1, yk
Вариант 24
1. Определить, принадлежит ли точка с координатами (x, y) заштрихованной части плоскости (рис. 1.24).
2. Для
x [–2,1; 3,2]
вычислить
3
3
2
sin cx x
. Значение c произвольное. Шаг
z
3
2 2
cx x 3,14
изменения x равен 0,2.
3. Вычислить x = f(y) – 0,3, где y = z + 2, а
y 3 0,3,
если y 0,
f ( y ) 0,
если 0 y 1,
y 2 y,
если y 1.
Рис. 1.24
x 2 0,5
4. Для x [–3,2; 3,2] вычислить z
. Шаг изменения x равен 0,2.
x 2 0,5
1
2
Значения x и z вывести в виде таблицы. Определить количество z, больших и
меньших нуля.
5. Дано натуральное число n. Вычислить
1
1
1
...
.
sin1 sin1 sin 2
sin1 sin 2 ... sin n
6. Вычислить
n
n
j i 1
.
i
j
i 1 j 1
7. Дано действительное число x. Последовательность a1 , a2 , ..., a j образована
( 1) n x n 1
по закону an
. Найти первый член последовательности, для которого
n!
выполняется условие an an 1 .
8. Даны действительные x, ε . Вычислить с точностью до
22
20.
k 0( 1) 2 k x k 2
(k 1)(k 2)!
Вариант 25
1. Определить, принадлежит ли точка с координатами (x, y) заштрихованной части плоскости (рис. 1.25).
sin x y
2. Для x [–1,6; 2,8] вычислить z
. Знаy cos x
чение y — произвольное. Шаг изменения x равен 0,1.
3. Для произвольного значения r вычислить
17 0,45r 2 ,
0,
y
18
,
r2
1
18
если r 12 0,
если r 12 0,
Рис. 1.25
если r 12 0.
4. Для x [–2,1; 2,1] вычислить y
1 1 sin x
. Шаг изменения x равен 0,2.
2
Значения x и y вывести в виде таблицы. Найти минимальное значение y на данном
интервале.
5. Дано действительное число x. Вычислить
( x 2)( x 4)( x 8)...( x 64)
.
( x 1)( x 3)( x 7)...( x 63)
6. Вычислить
n
1
(1 ) 2 .
i!
i 2
7. Пусть a1 b1 1, ak bk 1 ak 1 , bk ak2 1 bk2 1 , k = 2, 3, … Дано натуральное n ( n 2 ). Найти an, bn.
8. Даны действительные x, . Вычислить с точностью до
x
3
x 1
k 1 k k
1.2. Одномерные массивы
Вариант 1
1. Даны натуральное число n, действительные числа a1, …, an. Вычислить
23
21.
a1 +…+ an.2. Даны натуральное число n, действительные числа a1, …, an. Получить
числа b1, …, bn, которые связаны с a1, …, an следующим образом:
a a
b1 a1 , bn an , bi i 1 i , где
3
i = 2, …, n–1.
3. Даны целые числа c1, …, cn. Имеются ли в последовательности c1, …, cn
три идущих подряд нулевых члена?
4. Даны целые числа a1, …, an. Получить сумму тех чисел данной последовательности, которые кратны 5.
5. Даны действительные числа a1, …, a20. Преобразовать последовательность
по правилу: большее из ai и a10+i (i = 1, 2, …, 10) принять в качестве нового значения ai, а меньшее — в качестве нового значения a10+i.
6. Даны действительные числа a1, …, an (все числа попарно различны). Поменять в этой последовательности наибольший и наименьший члены.
Вариант 2
1. Даны натуральное число n, действительные числа a1, …, an. Вычислить
|a1| + |a2| + … + |an|.
2. Даны натуральное число n, действительные числа a1, …, an. Получить
b1, …, bn, где
ai
b1
, i = 1, 2, …, n.
1 (a1 ... ai ) 2
3. Даны натуральные числа n, b0, …, bn. Вычислить
f(b0) + f(b1) + … + f(b0),
где
x2 ,
если x кратно 3,
если x при делении на 3 дает остаток 1,
f(x) x,
x
в остальных случаях.
3
4. Даны натуральное число n, действительные числа a1, …, an. Выяснить, образуют ли числа возрастающую последовательность.
5. Даны целые числа a1, …, an среди которых могут быть повторяющиеся
члены. Найти число различных членов последовательности.
6. Даны действительные числа a1, a2, … Известно, что a1 > 0 и что среди
a2, a3, … есть хотя бы одно отрицательное число. Пусть a1, …, an — члены данной
последовательности, предшествующие отрицательному члену (n заранее не известно). Получить среднее арифметическое a1, …, an.
24
22.
Вариант 31. Даны натуральное число n, действительные числа a1, …, an. Вычислить
a1 a2 ... an .
2. Дано натуральное число n. Получить последовательность b1, …, bn, где
при i = 1, 2, …, n значение bi равно
1
( 1)i 1
1 ...
.
2
i
3. Даны натуральные числа i и n, действительные числа a1, …, an ( i n ) .
Найти среднее арифметическое всех чисел a1, …, an, кроме ai.
4. Даны целые числа a1, …, an (в последовательности могут быть повторяющиеся члены). Выяснить, сколько чисел входят в последовательность более чем
по одному разу.
5. Даны натуральные числа n, a1, …, an. Определить количество членов ak
последовательности a1, …, an, являющихся нечетными числами.
6. У прилавка в магазине выстроилась очередь из n покупателей. Время обслуживания продавцом i–го покупателя равно ti (i = 1, …, n). Пусть даны натуральное n и действительные t1, …, tn. Получить c1, …, cn, где ci — время пребывания i–го покупателя в очереди (i = 1, …, n). Указать номер покупателя, для обслуживания которого продавцу потребовалось самое малое время.
Вариант 4
1. Даны натуральное число n, действительные числа a1, …, an. Вычислить
a12 ... an2 .
2. Дано натуральное число n. Получить последовательность b1, …, bn, где
при i = 1, 2, …, n значение bi равно
1
1
1 ... .
2
i
3. Даны натуральное число n, действительные числа a1, …, an. Получить
max(a1, a1 + a2, a1 + a2 + a3, …, a1 + a2 + …+ an).
4. Даны натуральное число n, целые числа a1, …, an (в последовательности
могут быть повторяющиеся члены). Получить все числа, которые входят в последовательность по одному разу.
5. Даны натуральное число n, действительные числа x1, …, xn. Получить в
порядке следования все числа xk, удовлетворяющие неравенствам
xk > x1, xk > x2, …, xk > xk–1.
6. Даны целые числа a1, …, an, каждое из которых отлично от нуля. Если в
последовательности отрицательные и положительные члены чередуются, то ответом должна служить исходная последовательность. Иначе необходимо получить
все отрицательные члены последовательности, сохранив порядок их следования.
25
23.
Вариант 51. Даны натуральное число n, действительные числа a1, …, an. Вычислить
a1 a2 a3 ... ( 1) n 1an .
2. Дано натуральное число n. Получить последовательность b1, …, bn, где
при i = 1, 2, …, n значение bi равно
2i 1 .
3. Даны натуральное число n, действительные числа a1, …, an. В последовательности a1, …, an определить число соседств двух чисел различного знака.
4. Даны натуральное число n, действительные числа x1, …, xn. В последовательности x1, …, xn все члены, меньшие двух, заменить нулями. Кроме того, получить сумму членов, принадлежащих отрезку [3, 7], а также число таких членов.
5. Даны целые числа a1, …, an. Получить новую последовательность, удалив
из исходной все члены с максимальным значением.
6. Даны натуральное число n, действительные числа a, x1, …, xn
( x1 x2 ... xn ). Получить последовательность y1, …, yn+1, элементами которой
являются члены последовательности x1, …, xn и число a, такую, что
y1 y2 ... yn 1 .
Вариант 6
1. Дано натуральное число n. Получить последовательность b1, …, bn, в которой при i = 1, 2, …, n значение bi равно
2i 3i 1 .
2. Даны натуральное число n, действительные числа a1, …, an. Вычислить
a1 a2
( 1) n 1an
...
.
n!
1! 2!
3. Вычислить
30
(a b ) ,
i 1
2
i
i
где
если i нечетное,
i,
ai i
в противном случае,
2
i 2 ,
если i нечетное,
bi 3
в противном случае.
i
4. Даны натуральное число n, действительные числа a1, …, an. Получить удвоенную сумму всех положительных членов последовательности a1, …, an.
5. Даны натуральное число n, действительные числа a1, …, an. Получить
max( a1 , ..., an ) и
26
a12 ... an2 .
24.
6. Даны действительные числа a1, a2, …, an. Известно, что a1 > 0 и что средиa2, a3, … есть хотя бы одно отрицательное число. Пусть a1, …, aj — члены данной
последовательности, предшествующие первому отрицательному члену (j заранее
не известно). Получить количество четных чисел среди a1, …, aj.
Вариант 7
1. Даны действительные числа a1, …, an. Получить an, a1, a2, …, an–1.
2. Получить таблицу температур по Цельсию от 0 до 100 градусов и их эквивалентов по шкале Фаренгейта, используя для перевода формулу
9
tф tц 32 .
5
Результаты расчетов занести в массив.
3. Дано натуральное число n. Получить сумму тех чисел вида
i 2 3in 2 n (i = 1, 2, …, n),
которые являются утроенными нечетными.
4. Даны целые числа a, n, x1, …, xn (n > 0). Определить, каким по счету идет
в последовательности x1, …, xn член, равный a. Если такого члена нет, то ответом
должно быть число 0.
5. Даны действительные числа a1, …, an. Требуется умножить все члены последовательности a1, …, an на квадрат её наименьшего члена, если a1 0 , и на
квадрат наибольшего члена, если a1 0 .
6. Даны натуральное число n, действительные числа a1, …, an. Получить
b1, …, b10, где bi равно сумме тех членов последовательности, которые принадлежат полуинтервалу (i–1, i] (i = 1, …, 10). Если полуинтервал не содержит членов
последовательности, то соответствующее bi положить равным нулю.
Вариант 8
1. Даны действительные числа a1, …, a20. Получить последовательность
a1, a11, a12, a2, a3, a13, a14, a4, …, a9, a19, a20, a10.
2. Вычислить значения многочлена
x5 – 9x4 + 1,7x2 – 9,6
для x = 0, 1, …, 5. Результат вычислений занести в массив.
3. Даны натуральное число n, действительные числа a1, …, an. Получить
max(–a1, a2, –a3, (–1)n an).
4. Даны натуральное число n, действительные числа a1, …, an. Получить все
натуральные числа j ( 2 j n 1 ), для которых
aj–1 < aj > aj+1.
5. Даны целые числа a1, …, an среди которых могут быть повторяющиеся
члены. Выяснить, сколько чисел входит в последовательность по одному разу.
6. Даны действительные числа a1, a2, … , an Известно, что a1 > 0 и что среди
a2, a3, … есть хотя бы одно отрицательное число. Пусть a1, …, aj — члены данной
27
25.
последовательности, предшествующие первому отрицательному члену (j заранеене известно). Получить среднее геометрическое a1, …, aj.
Вариант 9
1. Даны действительные числа a1, …, a15. Получить
15
(a a )
i
15
2
ср
1
ai , S i 1
.
14
15 i 1
2. Даны действительные числа a1, a2, a3, a4, x1, …, xn. Получить b1, …, bn, по
следующему правилу:
xi2 xi a1 xi3 xi a2
xi4 xi a4
bi
xi (xi a3 ) ,
(xi a3 )
xi a1
xi a2
xi
где i = 1, 2, …, n.
3. Даны натуральные числа k, n, действительные числа a1, …, akn. Получить
последовательность
a1 +…+ ak, ak+1 +…+ a2k, …, ak(n–1)+1 +…+ akn.
4. Даны целые числа c1, …, cn. Имеются ли в этой последовательности два
идущих подряд нулевых члена? Указать их индексы.
5. Дано натуральное число n. Найти наибольшее среди чисел
2
kesin ( k 1) (k 1, n) ,
a также сумму всех этих чисел.
6. Даны натуральные числа n, a1, …, an. Определить количество членов ak
последовательности a1, …, an, являющихся квадратами четных чисел.
aср
Вариант 10
1. Даны натуральные числа n1, …, n20, действительные числа x1, …, x20. Вычислить
n1 x1 ... n20 x20
.
n1 ... n20
2. Вычислить последовательности значений функций
3x 2
5x2
P1 (x) x, P1 (x)
, P1 (x)
2
2
для значений аргумента x = 0; 0,05; 0,1; …; 20. Результаты расчетов занести в массив.
3. Даны действительные числа a1, …, an (все числа различны). Поменять
местами наибольший и последний члены.
4. Даны целые числа p, q, a1, …, an ( p q 0 ). В последовательности
a1, …, an заменить нулями члены, модуль которых при делении на p дает в остатке
q.
28
26.
5. Даны натуральные число n, целые числа a1, …, am и b1, …, bn. Средиa1, …, am нет повторяющихся чисел, нет их и среди b1, …, bn. Получить все члены
последовательности b1, …, bn, которые не входят в последовательность a1, …, am.
6. Даны действительные числа a1, …, an. Получить «сглаженные» значения
a1, …, an, произведя замену в исходной последовательности все члены, кроме перa a ai 1
вого и последнего, по формуле ai i 1 i
, i = 2, 3, …, n–1. При сглажива3
нии используются старые значения членов.
Вариант 11
1. Даны действительные числа a1, a2, …, a2n. Получить
a1 + a2n, a2 + a2n–1, …, an + an+1.
2. Даны натуральное число n, действительные a1, …, an. Вычислить
a1a2 ...an .
3. Даны натуральные числа k, n, действительные числа a1, …, akn. Получить
min(a1, …, ak), min(ak+1, …, a2k), …, min(ak(n–1), …, akn).
4. Даны натуральное число n, действительные числа a1, …, an. В последовательности a1, …, an все неотрицательные члены, не принадлежащие отрезку [1, 2],
заменить на единицу. Кроме того, получить количество отрицательных членов и
количество членов, принадлежащих отрезку [1, 2].
5. Даны действительные числа a1, …, an. Получить числа b1, …, bn, где bi —
среднее арифметическое всех членов последовательности a1, …, an, кроме ai
(i = 1, 2, …, n).
6. Даны целые числа a1, …, an. Если в последовательности ни одно четное
число
не
расположено
после
нечетного,
то
получить
все отрицательные члены последовательности, иначе — все положительные.
Вариант 12
1. Даны действительные числа a1, …, a20. Получить последовательность
a12, a2, a14, a4, a16, …, a20, a10.
2. Даны действительные числа a1, …, a2n. Получить
min(a1an+1, a2an+2, …, ana2n).
3. Даны натуральное число n, действительные числа y1, …, yn. Найти
z12 ... zn2 ,
где
yi
при yi 1,
zi 1
в противном случае.
y
i
4. Даны целые числа a1, …, an. Получить последовательность b1, …, bn, которая отличается от a1, …, an тем, что все нечетные члены исходной последова-
29
27.
тельности в ней удвоены.5. Даны натуральное число n, действительные числа a1, …, an.
Получить
min(a2, a4, …) + max(a1, a3, …).
6. Даны натуральное число n, действительные числа a1, …, an. Вычислить
обратную величину произведения тех членов ai последовательности a1, …, an, для
которых выполнено i+1 < ai < i.
Вариант 13
1. Даны действительные числа a1, a2, …, a2n. Получить
a1, a2n, a2, a2n–1, a3, …, an, an+1.
3a 4
для а = 1, 2, …, 100. Результа2. Вычислить значение выражения 2
a 5a 9
ты вычислений занести в массив.
3. Даны натуральное число n, действительные числа y1, …, yn. Найти
max(|z1|, …, |zn|), где
y
при yi 2,
zi i
в противном случае.
0,5
4. Даны натуральные числа n, a1, …, an. Определить количество членов ak
последовательности a1, …, an, имеющих четные порядковые номера и являющихся нечетными числами.
5. Даны целые числа a1, …, an среди которых могут быть повторяющиеся
члены. Выяснить, имеется ли в последовательности хотя бы одна пара совпадающих чисел.
6. Даны действительные числа a1, a2, … , an Известно, что a1 > 0 и что среди
a2, a3, … , an есть хотя бы одно отрицательное число. Пусть a1, …, aj — члены
данной последовательности, предшествующие первому отрицательному члену (j
заранее не известно). Получить
a1 + 2a2 + 2a3 +…+ 2aj–1 + aj.
Вариант 14
1. Даны действительные числа a1, a2, …, a2n. Получить
a1, an+1, a2, an+2, …, an, a2n.
2. Даны натуральное число n, действительные числа a, b ( a b ) Получить
r0, r1, …, rn, где
(b a )
ri a ih, h
.
n
3. Даны натуральное число n, действительные числа a1, …, an. Получить
min(a1, –a2, a3, (–1)n an).
4. Даны натуральное число n, действительные числа a1, …, an. Выяснить, образуют ли возрастающую последовательность числа
30
28.
a1, …, an, 2a1, 3a2, …, (n+1)an.5. Даны действительные числа a1, …, an. Получить последовательность
b1, …, bn, где
b1 a1 a2 ... an ,
b2 a12 a22 ... an2 ,
...
10
b2 a110 a10
2 ... an .
6. Даны действительные числа a1, …, an. Все члены этой последовательности, начиная с первого положительного, уменьшить на 0,5.
Вариант 15
1. Даны натуральное число n, действительные a1, …, an. Вычислить последовательность
a12 , a1a2 , a1a3 , ..., a1an .
2. Последовательность f0, f1, … образуется по закону
f0 = 1, f1 = 2, fi = fi–1 + fi–2 (i = 2, 3, …).
Дано натуральное n. Получить f0, f1, …, fn.
3. Даны натуральное число n, целые числа a1, …, an. Найти наименьшее из
четных чисел, входящих в последовательность
a1 –1, a1, a2, …, an.
4. Даны натуральные числа n, a1, …, an. Определить количество членов ak
последовательности a1, …, an, удовлетворяющих условию 2k < ak < k!, где
k!=1 2 3 4 ... k .
5. Даны натуральные числа k, n, действительные числа a1, …, akn. Получить
последовательность
max(a1, …, ak), max(ak+1, …, a2k), …, max(ak(n–1), …, akn).
6. Даны действительные числа a1, …, an. Если в результате замены отрицательных членов последовательности a1, …, an их квадратами члены будут образовывать неубывающую последовательность, то получить сумму членов исходной
последовательности, в противном случае получить их произведение.
Вариант 16
1. Даны действительные числа a1, …, a20. Получить
a20, a11, a19, a10, …, a10, a1.
2. Даны натуральное число n, действительные числа x1, …, xn ( n 2 ). Вычислить
1
1
1
(
x2 )(
x3 )...(
xn ).
x1 1
x2 1
xn-1 1
31
29.
(i 1)3i 1
sin
3. Пусть ai
(i = 1, 2, …). Дано натуральное n. Среди
i 1
i 1
a1, …, an найти все положительные числа; среди положительных чисел выбрать
наименьшее число.
4. Даны натуральные числа n, q1, …, qn. Найти те члены последовательности
q1, …, qn, которые обладают таким свойством, что корни уравнения
x2 + 3·qi – 5 = 0
действительны и положительны.
5. Даны натуральные числа k, n, действительные числа a1, …, akn. Получить
min(max(a1, …, ak), max(ak+1, …, a2k), …, max(ak(n–1), …, akn)).
6. Даны действительные числа a1, …, an, b1, …, bn. Члены последовательности c1, …, cn+1 связаны с членами данных последовательностей следующими соотношениями:
a( n 1) i
.
cn 1 0, c( n 1) i
b( n 1) i c( n 1) i 1
Получить c1, …, cn+1 (i = 1, …, 28).
Вариант 17
1. Даны действительные числа a1, …, an и b1, …, bn. Вычислить
(a1 + bn)(a2 + bn–1)…(an + b1).
2. Дано натуральное число n. Вычислить значения функции
x 2 3x 2
y
2 x3 1
для x = 1; 1,1; 1,2; …; 1+0,1·n. Результаты вычислений занести в массив.
3. Даны натуральное число n, действительные числа x1, …, x3n. Вычислить
сумму чисел xn+1, …, x3n, которые превосходят по величине все числа x1, …, xn.
4. Даны натуральное число n, целые числа a1, …, an. Получить сумму положительных и количество отрицательных членов последовательности a1, …, an.
5. Даны целые числа a1, …, an. Получить новую последовательность
из n чисел, заменяя ai нулями, если |ai| не равно max(a1, …, an), и заменяя ai единицей в противном случае (i = 1, …, n).
6. Даны действительные числа a1, …, an. Переставить члены последовательности a1, …, an так, чтобы сначала расположились все её неотрицательные члены,
а потом — все отрицательные. Порядок, как среди неотрицательных членов, так и
среди отрицательных, должен быть сохранен прежним.
a20.
Вариант 18
1. Даны действительные числа a1, …, a20. Получить a1, a3, …, a19, a2, a4, …,
2. Вычислить значения функции y = 4x3 – 2x2 + 5 для значений x, изменяющихся от –3 до 1 с шагом 0,1. Результаты расчетов занести в массив.
32
30.
3. Даны натуральное число n, действительные числа y1, …, yn. Найтиz z ... z z ,
2
1
2
n
1
n
где
при 0 yi 15,
y
zi i
2,7 в противном случае.
4. Даны действительные числа a1, a2, … Известно, что a1 > 0 и что среди
a2, a3, … есть хотя бы одно отрицательное число. Пусть a1, …, an — члены данной
последовательности, предшествующие первому отрицательному члену, n заранее
не известно. Получить
min(a1, 2a2, …, nan).
5. Даны натуральное число n, целые числа a1, …, an. Найти количество и
сумму тех членов данной последовательности, которые делятся на 5 и не делятся
на 7.
6. Даны натуральное число n, целые числа a1, …, an. Найти номер последнего нечетного члена последовательности a1, …, an; если нечетных чисел нет, то ответом должно быть число n+1.
Вариант 19
1. Даны натуральное число n, действительные числа a1, …, an. Вычислить
a1 , a2 , a3 , ..., ( 1) n an .
2. Последовательность чисел Фибоначчи u0, u1, … образуется по закону
u0 = 0, u1 = 1, ui = ui–1 + ui–2 (i = 2, 3, …).
Дано натуральное число n > 1. Получить u0, u1, …, un.
3. Даны натуральное число n, действительные числа a1, …, an. Верно ли, что
отрицательных членов в последовательности a1, …, an больше, чем положительных?
4. Даны натуральное число n, действительные числа a1, …, an. Найти
min(|z1|, …, |zn|),
где
a
при ai 1,
zi i
в противном случае.
2
5. Даны натуральное число n, целые числа a1, …, a10 и b1, …, bn. Среди
a1, …, a10 нет повторяющихся чисел, нет их и среди b1, …, bn. Верно ли, что все
члены последовательности b1, …, bn входят в последовательность a1, …, a10.
6. Даны действительные числа a1, a2, … , an. Известно, что a1 > 0 и что среди
a2, a3, … есть хотя бы одно отрицательное число. Пусть a1, …, aj — члены данной
последовательности, предшествующие первому отрицательному члену (j заранее
не известно). Получить
a1a2 + a2a3 +…+ an–1aj + aja1.
33
31.
Вариант 201. Даны натуральное число n, действительные a1, …, an. Вычислить
a1, a1 + a2, a1 + a2 + a3, …, a1 + a2 +…+ an.
2. Последовательность x1, x2, … образована по закону
x1 x2 x3 1, xi (i 3)(xi 1 1) (i 4)xi 3 ,
где i = 4, 5, … Получить x1, x2, …, x20.
3. Даны действительные числа a1, …, an. Получить
min(a1, a3, a5, …).
4. Даны натуральное число n, целые числа a1, …, an. Найти наибольшее из
нечетных чисел и количество четных чисел, входящих в последовательность
a1, …, an, an+1.
5. Даны натуральное число n, целые числа a1, …, a10 и b1, …, bn. Среди
a1, …, a10 нет повторяющихся чисел, нет их и среди b1, …, bn. Верно ли, что все
члены последовательности a1, …, a10 входят в последовательность b1, …, bn.
6. Даны действительные числа a1, …, an. Оставить без изменения последовательность a1, …, an, если она упорядочена по убыванию; в противном случае удалить из последовательности те члены, порядковые номера которых кратны четырем, сохранив прежним порядок оставленных членов.
Вариант 21
1. Даны натуральное число n, действительные числа a1, …, an. Вычислить
a1, –a1a2, a1a2a3, …, (–1)n+1a1a2…an.
2. Последовательность x1, x2, … образована по закону
x1 1, x2 0 ,3, xi (i 1) xi 2 (i = 3, 4, …).
Получить x1, x2, …, x20.
3. Даны натуральное число n, действительные числа y1, …, yn. Найти
z1, …, zn, где
при 0 yi 10,
y
zi i
в противном случае.
1
4. Даны натуральные числа a1, …, an. Определить количество членов ak последовательности a1, …, an, удовлетворяющих условию
a a
ak k 1 k 1 .
2
5. Даны целые числа a1, …, an. Пусть M — наибольшее, а m — наименьшее
из a1, …, an. Получить в порядке возрастания все целые числа из интервала (m, M),
которые не входят в последовательность a1, …, an.
6. Даны действительные числа x1, …, xn и y1, …, yn. Получить действительные числа a1, …, an и b1, …, bn, преобразовав для получения ai, bi члены xi, yi по
правилу: если они оба отрицательны, то каждый из них увеличить на 0,5; если отрицательно одно из них, то отрицательное число заменить его квадратом; если оба
34
32.
числа неотрицательны, то каждое из них заменить на среднее арифметическое исходных значений.Вариант 22
1. Даны действительные числа a1, …, a30. Получить
max(a1 + a30, a2 + a29, …, a15 + a16).
2. Цилиндр с объемом равным единице имеет высоту h, Определить радиус
основания цилиндра для значений h, равных 0,5; 1; 1,5; …, 5.
3. Пусть
a0 = cos21, a1 = –sin21, ak = 2ak–1 – ak–2 (k = 2, 3, …).
Найти сумму квадратов тех чисел a1, …, a100, которые не превосходят 2.
4. Даны натуральное число n, действительные числа a1, …, an. В последовательности a1, …, an определить число соседств двух чисел одного знака, причем
модуль первого числа должен быть больше модуля второго числа.
5. Даны целые числа a1, …, an. Все члены последовательности с четными
номерами, предшествующие первому по порядку члену со значением
max(a1, …, an), домножить на max(a1, …, an).
6. Даны целые числа a1, …, an. Наименьший член последовательности
a1, …, an заменить целой частью среднего арифметического всех членов, остальные члены оставить без изменения. Если в последовательности несколько членов
со значением min(a1, …, an), то заменить только последний член.
Вариант 23
1. Даны натуральное число n, действительные числа x1, …, xn. Вычислить
(x1 + 2x2 + x3)(x2 + 2x3 + x4)…(xn–2 + 2xn–1 + xn).
2. Даны действительные числа x1, …, xn и y1, …, yn. Получить
n
x y .
i 1
i
i
3. Даны натуральное число n, целые числа a1, …, an. Заменить все члены последовательности a1, …, an, большие семи, числом 7. Вычислить количество таких
членов.
4. Даны натуральное число n, действительные числа a1, …, an. В последовательности a1, …, an все отрицательные члены увеличить на 0,5, а все неотрицательные заменить на 0,1.
5. Даны действительные числа a1, a2, …, an. Известно, что a1 > 0 и что среди
a2, a3, …, an есть хотя бы одно отрицательное число. Пусть a1, …, aj — члены данной последовательности, предшествующие первому отрицательному числу
(j заранее не известно). Получить max( a13 , ..., a 3j ).
6. Даны натуральное число n, целые числа a1, …, an. Найти номер первого
четного члена последовательности a1, …, an. Если четных членов нет, то ответом
должно быть число 0.
35
33.
Вариант 241. Даны натуральное число n, действительные числа x1, …, xn ( n 3 ). Вычислить
(x1 + x2 + x3)x2 + (x2 + x3 + x4)x3 +…+ (xn–2 + xn–1 + xn)xn–1.
2. Даны действительные числа a1, …, a17. Получить
a11, a12, …, a17, a10, a9, …, a1.
3. Даны натуральное число n, действительные числа y1, …, yn. Найти
z1, …, zn, где
при 0 yi 10,
y
zi i
в противном случае.
1
4. Даны натуральное число n, целые числа a, x1, …, xn. Если в последовательности x1, …, xn есть хотя бы один член, равный a, то получить сумму всех
членов, следующих за первым таким членом; в противном случае ответом должно
быть число 10.
5. Даны действительные числа a1, a2, … Известно, что a1 > 0 и что среди
a2, a3, … есть хотя бы одно отрицательное число. Пусть a1, …, an — члены данной
последовательности, предшествующие первому отрицательному числу (n заранее
не известно). Получить max(a1, a1a2, …, a1a2…an).
6. Даны натуральное число n, целые числа a1, …, an. Выяснить, какое число
встречается в последовательности a1, …, an раньше — положительное или отрицательное. Если все члены последовательности равны нулю, то сообщить об этом.
Вариант 25
1. Даны действительные числа a1, …, a20. Получить a1, a11, a3, a13, …, a9, a19.
2. Даны натуральное число n, действительные числа a, b (b > a > 0). Получить последовательность действительных чисел y0, y1, …, yn, где
(b a )
.
yi xi , xi a ih, h
n
3. Даны натуральнее число n, действительные числа a1, …, an. Выяснить, образуют ли возрастающую последовательность числа
a1, …, an, n(an–1 + 1), (n – 1)(an–2 + 2), …, 2(a1 + n – 1).
4. Даны натуральные числа m, n, действительные числа a1, a2, a3, …, amn.
Вычислить
a1a2…am + am+1am+2…a2m + …+a(n–1)m+1 a(n–1)m + 2amn.
5. Даны натуральное число n, действительные числа a1, …, an. Верно ли, что
наибольший член последовательности a1, …, an по модулю больше единицы?
6. Даны действительные числа a1, a2, … Известно, что a1 > 0 и что среди
a2, a3, … есть хотя бы одно отрицательное число. Пусть a1, …, an — члены данной
последовательности, предшествующие первому отрицательному числу (n заранее
не известно). Получить max( a12 , ..., an2 1 ).
36
34.
1.3. Двухмерные массивыВариант 1
1. Даны натуральное число n , действительная матрица A размером n n и
вектор b размером n . Вычислить max (aij ) среди элементов, лежащих выше главной диагонали, min(b i ) среди элементов, больших нуля, и найти отношение
max(aij )
.
d
min(bi )
2. Даны две матрицы размером n m . Получить новую матрицу прибавлением к элементам каждого столбца первой матрицы произведения соответствующей строки второй матрицы. Для нахождения произведения и суммы использовать подпрограммы.
3. Дана квадратная матрица A размером n n . Получить вектор b1 , ..., bn , где
bi — наименьшее из значений элементов, находящихся в начале i -й строки матрицы до элемента, принадлежащего главной
диагонали включительно. Для нахождения минимального элемента использовать подпрограмму.
4. Получить целочисленную квадратную матрицу порядка
7, элементами которой являются числа 1, 2, 3, …, 47, располоРис. 1.26
женные по спирали (рис. 1.26).
Вариант 2
1. Даны две квадратные матрицы A и B размером n n . Вычислить сумму
элементов, лежащих на главной диагонали матрицы {cij } , образованной следующим
образом:
cij aij bij .
2. Даны действительные числа a1 , ..., an ; b1 , ..., bn . В последовательности
a1 , ..., an и в последовательности b1 , ..., bn все отрицательные члены, следующие за
членом с наибольшим значением, заменить на 0,5. Для поиска наибольшего значения и замены элементов использовать подпрограммы.
3. Дана целочисленная квадратная матрица A порядка n . Найти номера
строк, все элементы которых четны.
4. Даны действительные числа a1 , ..., a64 . Получить действительную квадратную матрицу порядка 8, элементами которой
являются числа a1 , ..., a64 , расположенные по схеме, представленной на рис. 1.27.
Рис. 1.27
37
35.
Вариант 31. Даны натуральные k и n , действительные числа a1 , a2 , ..., ak n . Получить
max(a1 ... ak , ak 1 ... a2 k , ..., ak ( n 1) 1 ... ak n ).
2. Дано действительное число y . Получить
1,7t (0,25) 2t (1 y )
,
z
6 t (y 2 1)
где
x 2 k 1
.
t ( x)
k 0 (2 k 1)!
Для нахождения значений функции t , суммы и факториала использовать подпрограммы. Результаты вычислений занести в массив.
3. Дана вещественная квадратная матрица A порядка n и вектор b размером n . Найти вектор
c b A
и
min{b12 , b22 , ..., bn2 }
d
max{ c1 , c2 , ..., cn }
Для нахождения минимального и максимального значений использовать подпрограммы. Вектор вычисляется следующим образом:
10
n
ci bi aij .
j 1
4. Даны действительные числа a1 , ..., a64 . Получить действительную квадратную матрицу порядка 8, элементами которой являются числа a1 , ..., a64 , расположенные по схеме, представленной на рис. 1.28.
Рис. 1.28
Вариант 4
1. В действительной квадратной матрице A порядка n найти сумму элементов строки, в которой расположен элемент с наименьшим значением.
2. Дан массив a1 , ..., an . Отсортировать массив по возрастанию, используя
следующий алгоритм: последовательным просмотром чисел a1 , ..., an найти наименьшее i такое, что ai ai 1 ; поменять местами ai и ai 1 и возобновить просмотр
с начала массива; когда не удаться найти такое i , массив будет упорядочен нужным образом. Алгоритм сортировки реализовать, используя подпрограмму.
3. Дана вещественная квадратная матрица A порядка n . Из матрицы удалить i -ю строку и j -й столбец. Для поиска нужной строки и столбца, а также для
сжатия матрицы использовать подпрограммы.
38
36.
4. Даны действительные числа a1 , ..., a64 . Получить действительную квадратную матрицу B порядка 8, элементами которойявляются числа a1 , ..., a64 , расположенные по схеме, представленной на рис. 1.29.
Рис. 1.29
Вариант 5
1. Даны натуральные числа k , n , действительные числа a1 , a2 , ..., ak n . Получить
min(max(a1 , ..., ak )) , max(ak 1 , ..., a2 k ) , …, max(ak (n 1) 1 , ..., akn )) .
2. Даны действительные числа x1 , y1 , x2 , y2 , …, x10 , y10 . Найти периметр
десятиугольника, вершины которого имеют соответственно координаты
( x1 , y1 ), …, ( x10 , y10 ). Вычисления расстояния между двумя точками, заданными
координатами, организовать с помощью подпрограммы.
3. Дана целочисленная квадратная матрица B порядка n .
Найти номера строк, элементы в каждой из которых одинаковы.
Для поиска номеров строк использовать подпрограммы.
4. Даны действительные числа a1 , ..., a64 . Получить действительную квадратную матрицу B порядка 8, элементами которой
являются числа a1 , ..., a64 , расположенные в по схеме, представленРис. 1.30
ной на рис. 1.30.
Вариант 6
1. Дана квадратная матрица A порядка n . Найти максимальный элемент в
строках, имеющих положительный элемент на главной диагонали.
2. Дана действительная матрица B размера n m . Переставить строки матрицы по убыванию значений наибольших элементов строк. Для поиска наибольших элементов и перестановки строк использовать подпрограммы.
3. Даны натуральное число n , действительное число x , действительная
матрица размером n 2n . Получить последовательность b1 , ..., bn из
нулей и единиц, где bi = 1, если элементы i -й строки матрицы не
превосходят x , и bi = 0 в противном случае. Для сравнения элементов матрицы с числом x пользовать подпрограмму.
4. Дана действительная квадратная матрица B порядка n .
Найти наибольшее из значений элементов, расположенных в заштрихованной части матрицы (рис. 1.31).
Рис. 1.31
39
37.
Вариант 71. Даны натуральное число m , целые числа a1 , ..., am и целочисленная квадратная матрица B порядка m . Найти минимальный элемент в отмеченных строках матрицы. Строку i назовем отмеченной, если ai 0 .
2. Даны натуральные числа k , l , m , действительные числа x1 , ..., xk ;
y1 , ..., yl ; z1 , ..., zm . Получить
max( y1 , ..., yl ) max( z1 , ..., zm ) при max( x1 ,..., xk ) 0,
t
2
в остальных случаях.
1 max( x1 , ..., xk )
Для нахождения максимального элемента использовать подпрограмму.
3. Даны две квадратные целочисленные матрицы A и B порядка n . Найти
последовательность b1 , ..., bn , в которой: bi = 1, когда i -е строки первой и второй
матриц содержат вместе не более трех положительных элементов,
и bi = 0 в противном случае. Для нахождения количества положительных элементов в строке использовать подпрограмму.
4. Дана действительная квадратная матрица B порядка n .
Найти наибольший элемент, расположенный в заштрихованной
части матрицы (рис. 1.32).
Рис. 1.32
Вариант 8
1. Даны натуральное число n , матрица A размером n n , вектор b размером n . Определить вектор z1 , ..., zn такой, что
bi
min a , i 1, n; j 1, n , если min aij 1,
zi
ij
b
в противном случае.
i
2. Дана действительная матрица B размером n m . Расположить строки
матрицы по возрастанию значений наименьших элементов строк. Для поиска
наименьшего элемента строки и перестановки строк использовать
подпрограммы.
3. Дана квадратная матрица A размером n n . Найти номера
строк, все элементы которых отрицательны. Для поиска номеров
строк использовать подпрограмму.
4. Дана действительная квадратная матрица B порядка n .
Найти наибольшее из значений элементов, расположенных в заРис. 1.33
штрихованной части матрицы (рис. 1.33).
Вариант 9
1. Даны натуральное число m , целые числа a1 , ..., am и целочисленная квадратная матрица A порядка m . Строку с номером i назовем отмеченной, если
40
38.
ai 0 , и неотмеченной — в противном случае. Найти сумму положительных элементов в отмеченных строках матрицы.2. Даны натуральное число n и две матрицы A и B размером n n . Вычислить
max{aij } max{bij }
,
z
max{cij }
где
cij aij bij .
Для нахождения матрицы C и максимального элемента использовать подпрограммы.
3. Дана вещественная квадратная матрица X размером n . Вычислить вектор
b такой, что
bi x1i min( xij ) .
Для нахождения минимального элемента и получения вектора b
использовать подпрограммы.
4. Дана действительная квадратная матрица A порядка n .
Найти наибольший элемент, расположенный в заштрихованной
части матрицы (рис. 1.34).
Рис. 1.34
Вариант 10
1. Вычислить суммы элементов каждой строки матрицы A размером n m
и определить наименьшее значение из этих сумм, а также номер соответствующей
строки.
2. Даны натуральные числа n и m , целые числа a1 , ..., an ; b1 , ..., bm ; c1 , ..., c10 .
Получить
при min(a1 , ..., an ),
min(b1 , ..., bm ) min(c1 , ..., c10 )
z
2
в противном случае.
1 max (c1 , ..., c10 )
Для нахождения минимального и максимального элементов использовать подпрограммы.
3. Дана целочисленная матрица A порядка n . Получить b1 , ..., bn , где bi —
это сумма элементов, предшествующих последнему отрицательному элементу i-й
строки. Если все элементы строки неотрицательны, принять
bi = –1.
Для нахождения суммы элементов и номера строки с отрицательным элементом использовать подпрограммы.
4. Дана действительная квадратная матрица A порядка n .
Найти наибольшее из значений элементов, расположенных в заштрихованной части матрицы (рис. 1.35).
Рис. 1.35
41
39.
Вариант 111. Дана действительная квадратная матрица A порядка n . Назовем допустимым преобразованием матрицы перестановку двух строк или двух столбцов. С
помощью допустимых преобразований добиться того, чтобы один из элементов
матрицы, обладающий наибольшим по модулю значением, располагался в левом
верхнем углу.
2. Дана действительная квадратная матрица B порядка n . Построить последовательность a1 , ..., an по правилу: если в i -й строке матрицы B элемент, принадлежащий главной диагонали, отрицателен, то ai равно сумме элементов,
предшествующих диагональному; в противном случае — сумме элементов, стоящих за диагональным. Для нахождения суммы использовать подпрограмму.
3. Дана действительная матрица A размером n m . Получить последовательность b1 , ..., bn , где bi — это произведение квадратов тех элементов строк матрицы, модули которых принадлежат интервалу
[1,1; 2,1], Для нахождения произведения использовать подпрограмму.
4. Дана действительная квадратная матрица B порядка n .
Найти наибольшее из значений элементов, расположенных в заРис. 1.36
штрихованной части матрицы (рис. 1.36).
Вариант 12
1. Даны целые n и матрица C размером n n . Найти максимальный элемент среди отрицательных элементов матрицы C и поменять его местами с первым элементом. Предполагается, что максимальный элемент единственный.
2. Даны натуральное число n , целые числа a1 , ..., an . Найти наибольшее значение, встречающееся в последовательности после удаления из нее всех членов со
значением max(a1 , ..., an ) . Для нахождения максимального элемента и сжатия последовательности использовать подпрограммы.
3. Дана действительная матрица A размером n m . Найти
среднее арифметическое каждого столбца матрицы. Для нахождения суммы элементов и среднего арифметического использовать
подпрограмму.
4. Дана действительная квадратная матрица B порядка n .
Найти наибольшей из элементов, расположенных в заштрихованРис. 1.37
ной части матрицы (рис. 1.37).
Вариант 13
1. Дана последовательность положительных чисел x1 , x2 , ..., xn ( n заранее не
известно), за которыми следует отрицательное число. Вычислить
42
40.
nx1 (n 1) x2 ... 2 xn 1 xn .2. Расстояние между k -й и l -й строками матрицы A определяется как
n
a a .
j 1
kj
lj
Указать номер строки, максимально удаленной от первой строки матрицы. Для
поиска максимального элемента использовать подпрограмму.
3. Дана действительная матрица {aij } размером n n . Получить действительную матрицу {bij }, i, j 1, n , элемент которой равен сумме элементов данной матрицы, расположенных в области,
определяемой индексами i, j , как показано на рис. 1.38 в заштрихованной области.
4. Даны действительные числа a1 , ..., an . Получить следующую квадратную матрицу порядка n :
a1 a2 a3 ... an 2 an 1 an
a a a ... a
an
a1
3
4
n 1
2
a3 a4 a5 ... an
a1
a2 .
...
...
... ... ... ... ...
an a1 a2 ... an 3 an 2 an 1
Рис. 1.38
Вариант 14
1. Дана квадратная целочисленная матрица A порядка n . Определить индексы всех элементов с наибольшим значением.
2. Дана матрица B порядка n . Найти наименьшее из значений элементов
столбца, который обладает наибольшей суммой модулей элементов.
3. Дана действительная матрица C размера n n , все элементы которой различны. В каждой строке выбирается элемент с наименьшим значением, затем среди этих значений выбирается наибольший. Указать номер строки элемента с найденным значением.
4. Даны целые числа a1 , ..., an . Пусть M — наибольшее из чисел a1 , ..., an ;
m — наименьшее из a1 , ..., an . Получить в порядке возрастания все целые числа из
интервала (m, M ) , которые не входят в последовательность a1 , ..., an .
Вариант 15
1. Дана действительная квадратная матрица A размера n n . Получить целочисленную квадратную матрицу B того же размера, в которой элемент равен
единице, если соответствующий ему элемент матрицы A больше элемента, рас43
41.
положенного в той же строке на главной диагонали, и равен нулю в противномслучае.
2. Дана вещественная матрица B размером m n . Получить сумму наибольших и наименьших значений каждой строки. Для нахождения наибольшего и
наименьшего значений строк и суммы использовать подпрограммы.
3. Дана вещественная квадратная матрица A порядка n и вектор b размером n . Определить сумму положительных элементов вектора c b A . Для нахождения значений вектора использовать подпрограмму. Вектор c :
n
ci bi aij .
j 1
4. Дана действительная квадратная матрица порядка n . Получить наибольший из элементов, расположенный в заштрихованной части матрицы (рис. 1.39).
Рис. 1.39
Вариант 16
1. Даны два одномерных массива a и b размером n . Если массивы равны,
то в массив {ci }, i 1, n записать их сумму, иначе в массив {ci } переписать элементы массива ai .
2. Даны действительные числа ai , i 1, n , действительная матрица A порядка n . Получить действительную матрицу B размера (n 1) n , вставив в исходную матрицу новую строку ai , не нарушая упорядоченности. Строки матрицы упорядочены по возрастанию значения первого элемента.
3. Дана действительная матрица A размера n n . Получить
действительную матрицу B размера n n , элемент которой равен
сумме элементов данной матрицы, расположенных в области, определяемой индексами i, j , как показано на заштрихованной области (рис. 1.40).
Рис. 1.40
4. Дано действительное число х. Получить квадратную матрицу A порядка 10:
1
x
...
8
x
x9
x
... x8
0
...
0
... ... ...
0
...
0
8
...
x
x
x9
x8
... .
x
1
Вариант 17
1. Найти норму квадратной матрицы A порядка n по следующей формуле:
44
42.
nнорма max aij .
i , j 1
2. Дана матрица A размером n n . Переменной y присвоить значение, равное скалярному произведению строки на столбец, на пересечении которых находится наименьший элемент матрицы. Для нахождения наименьшего элемента, а
также скалярного произведения использовать подпрограммы.
3. Дан вещественный массив b размером n . Удалить из
него элемент с номером k . Для сжатия массива использовать
подпрограмму.
4. Дана действительная квадратная матрица C порядка 7.
Найти последовательность чисел b1 , ..., b49 , получающуюся при
чтении матрицы по спирали, как показано на рис. 1.41.
Рис. 1.41
Вариант 18
1. Дана действительная квадратная матрица A порядка n . Преобразовать её
по правилу: строку с номером k сделать столбцом с номером k , а столбец с номером k сделать строкой с тем же номером. Значение k произвольное.
2. Дана вещественная матрица B размером m n . Найти суммы положительных элементов в строках, начинающихся с отрицательного элемента. Для поиска суммы использовать подпрограмму.
3. Дана вещественная матрица C размером m n . Найти максимальный
элемент среди отрицательных элементов матрицы. Для поиска максимального
элемента использовать подпрограмму нахождения максимального элемента среди
элементов одномерного массива.
4. Получить квадратную матрицу D порядка n :
0
n
0 n 1
... ...
0
0
... 0
... 0
.
... ...
... 1
Вариант 19
1. Дана вещественная матрица A размером m n . Вычислить элементы одномерного массива {bi }, где i 1, m, такого, что
первый отрицательный элемет i -й строки матрицы A,
bi
1, если в i -й строке матрицы нет отрицательных элементов.
2. Даны натуральное n , вещественная матрица A размером n n и вектор b
размером n . Определить вектор z z1 , ..., zn , где
45
43.
bi, если ai1 1,
zi min{aij }
b
в противном случае.
i
Для нахождения минимального элемента использовать подпрограмму.
3. Дана вещественная квадратная матрица C порядка n .
Для данного натурального m (m 2n) найти сумму тех элементов матрицы, сумма индексов которых равна m . Для нахождения суммы использовать подпрограмму.
4. Дана действительная квадратная матрица D порядка
2n . Получить новую матрицу, переставляя её блоки размера
Рис. 1.42
n n , как показано на рис. 1.42.
Вариант 20
1. Даны натуральное число n , вещественная матрица A размером n n ,
вектор b размером n . Вычислить p s v , где s — скалярное произведение первого столбца матрицы A на вектор b ; v — скалярное произведение последней
строки матрицы на вектор b .
2. Даны две действительные квадратные матрицы B и C порядка n . Получить новую матрицу прибавлением к элементам каждого столбца первой матрицы
произведения элементов соответствующих строк второй матрицы. Для нахождения суммы и произведения использовать подпрограммы.
3. Дана вещественная матрица D размером m n . Найти
минимальный элемент матрицы и сумму положительных элементов строки, на которой он находится. Для нахождения минимального элемента и суммы использовать подпрограммы.
4. Дана действительная квадратная матрица A порядка 2n .
Получить новую матрицу, переставляя ее блоки размера n n ,
как показано на рис. 1.43.
Рис. 1.43
Вариант 21
1. Даны натуральное n , вещественная матрица A размером n n , вектор b
размером n . Определить вектор
b b
b
c 1 , 2 , ..., n ,
g
g g
где
максимальный элемент матрицы A из интервала [2,5; 6,8],
g
1, если таких элементов нет.
46
44.
2. Дана матрица A размером m n . Вычислить элементы одномерного массива {b j }, где j 1, n такого, чтосумма элементов j-го столбца, если a1,j 1,
bj
в остальных случаях.
1
Для нахождения суммы использовать подпрограмму.
3. Дан одномерный вещественный массив ai размером n . Создать массив
bi , в который переписать элементы массива ai , меньшие некоторого числа m .
Для формирования массива bi использовать подпрограмму.
4. Даны действительная матрица B размера n (n 1) , действительные числа a1 , ..., an 1 и b1 , ..., bn 1 , натуральные числа p, q ( p n, q n 1) . Образовать новую матрицу размера (n 1) (n 2) вставкой после строки с номером p матрицы
B новой строки с элементами a1 , ..., an 1 и последующей вставкой после столбца с
номером q , нового столбца с элементами b1 , ..., bn 1 .
Вариант 22
1. Дана матрица A и вектор b размера n . Определить
n
si aij
j 1
для строк матрицы A , если bi 0 .
2. Дана действительная матрица C размера n m . Переставить строки матрицы по убыванию сумм элементов строк. Для нахождения суммы и перестановки
строк использовать подпрограммы.
3. Даны две вещественные матрицы A и B размером n n . Определить
1, если max{aij } max{bij },
d
0 в противном случае.
Для нахождения максимального элемента использовать подпрограмму.
4. Получить квадратную матрицу D порядка n :
0
1 2 0 ...
0 2 3 ...
0
.
0
0 ...
0
0 ... n(n 1)
0
Вариант 23
1. Дана целочисленная матрица A размера m m . Получить b1 , ..., bm , где
47
45.
bi a jij
для тех элементов с индексом j , для которых выполняется неравенство
1 a ji m .
2. Дана действительная матрица C размера n m . Переставить строки матрицы по возрастанию значений первых элементов строк. Для поиска минимального элемента использовать подпрограмму.
3. Дана вещественная матрица A размером n n . Переменной t присвоить
значение, равное скалярному произведению векторов x и y , компоненты которых определяются следующим образом: x i max{aij }, y j min{aij } . Для поиска
минимального, максимального элементов и вычисления скалярного произведения
использовать подпрограммы.
4. Получить квадратную матрицу D порядка n :
2
1
...
0
0
1 ... 0
0 ... 0
... ... ...
0 ... 0
0 ... 1
0
0
... .
1
2
Вариант 24
1. Даны две целочисленные матрицы A и B размера n n . Найти последовательность b1 , ..., bn , состоящую из нулей и единиц. Условие следующее: bi 1 ,
если количество отрицательных и неотрицательных элементов i -й строки первой
матрицы совпадает соответственно с количеством отрицательных и неотрицательных элементов i -й строки второй матрицы; bi 0 противном случае.
2. В данной действительной квадратной матрице C порядка n найти наибольший по модулю элемент. Получить квадратную матрицу порядка n 1 путем
удаления из исходной матрицы строки и столбца, на пересечении которых находится элемент с найденным значением. Для поиска наибольшего элемента и сжатия матрицы использовать подпрограммы.
3. Дана вещественная матрица A размером m n и вещественная матрица
B размером m1 n1 . Вычислить одномерный массив c {c1 , с2 } такой, что с1 равен
сумме элементов матрицы A , с2 — сумме элементов матрицы B . Найти максимальную из найденных сумм. Для поиска суммы использовать подпрограммы.
4. Получить квадратную матрицу D порядка n :
48
46.
11
...
1
1
1 ... 1
0 ... 1
... ... ... .
0 ... 1
1 ... 1
Вариант 25
1. Дана действительная квадратная матрица A порядка n . В строках, начинающихся с отрицательного элемента, найти суммы элементов строк.
2. Дана матрица A размером m n . Упорядочить каждую строку матрицы
по убыванию элементов строк. Для сортировки строк матрицы использовать подпрограмму сортировки элементов одномерного массива.
3. Дана вещественная матрица A размером m n . Найти максимальный
элемент среди положительных элементов матрицы. Для поиска положительных
элементов и максимального элемента использовать подпрограммы.
4. Получить квадратную матрицу B порядка n :
1 1 1 1 ... 1
2 2 2 ... 2 0
3 3 ... 3 0 0
.
...
...
...
0
0
0
... ... 0 0 0 0
n 0 0 0 0 0
1.4. Строки
Вариант 1
1. Даны натуральное число n, символы s1, …, sn. Преобразовать последовательность s1, …, sn, удалив каждый символ « » и повторив каждый символ, отличный от « ».
2. Дана строка символов. Группы символов, разделенные одним или несколькими пробелами и не содержащие пробелы внутри себя, будем называть
словами. Найти длину самого короткого слова.
3. Составить программу определения порядкового номера заданного слова в
множестве слов. Множество слов представлено в виде строки символов заданного
размера. Слова в строке отделены символом пробела.
4. Багаж пассажира характеризуется количеством вещей и их общим весом.
Дан массив, содержащий сведения о багаже нескольких пассажиров. Выяснить,
49
47.
имеется ли пассажир, багаж которого превышает багаж каждого из пассажиров ипо числу вещей и по весу.
5. Сведения о служащих содержат фамилию, адрес, дату приема на работу,
годовой заработок и номер отдела. Задан годовой фонд заработной платы отдела.
Выяснить, можно ли принять на работу нового сотрудника. Если да, то с каким
годовым заработком?
Вариант 2
1. Даны натуральное число n и символы s1, …, sn, среди которых есть двоеточие. Получить все символы, расположенные до первого двоеточия включительно.
2. Дана строка символов. Группы символов, разделенные одним или несколькими пробелами и не содержащие пробелы внутри себя будем называть словами. Преобразовать строку, заменяя каждое вхождение слова «это» на слово
«то».
3. Составить программу извлечения слова из множества слов по порядковому номеру. Множество слов представлено в виде строки символов заданного размера. Слова в строке отделены символом пробел.
4. Багаж пассажира характеризуется количеством вещей и общим весом вещей. Дан массив, содержащий сведения о багаже нескольких пассажиров. Выяснить, имеется ли пассажир, багаж которого состоит из одной вещи весом не менее
30 кг.
5. Сведения о служащих содержат фамилию, адрес, дату приема на работу,
годовой заработок и номер отдела. Найти служащего с наименьшим годовым заработком.
Вариант 3
1. Даны натуральное n, символы s1, …, sn. Преобразовать последовательность s1, …, sn, заменив в ней все вхождения букв «abc» на буквы «def».
2. Даны символьные строки f, g. Определить, совпадают ли символы строки
f с символами строки g. Если нет, то получить номер первого символа, в котором
строки f и g отличаются между собой. В случае, когда одна из строк имеет n символов ( n 0 ) и повторяет начало другой более длинной отроки, ответом должно
быть число n+1.
3. Составить программу обмена местами двух указанных слов во множестве
слов. Слова могут быть различной длины. Множество слов представлено в виде
строки символов. Слова в строке отделены символом пробел.
4. Сведения об автомобиле состоят из его марки, номера и фамилии владельца. Дан массив, содержащий сведения о нескольких автомобилях. Найти фамилии владельцев и номера автомобилей данной марки.
5. Даны сведения об учащихся: шифр класса, шифр дисциплины, количество
отличных оценок, количество хороших оценок, количество удовлетворительных и
50
48.
неудовлетворительных оценок, пропущено лекций, пропущено практических занятий. Вывести входные данные в виде табл. 1.1.Таблица 1.1
Шифр
класса
Средний
балл
Всего
Пропущено занятий
в том числе
Лекций
Практических
Вариант 4
1. Даны натуральное число n, символы s1, …, sn. Заменить в этой последовательности каждую группу букв «child» группой букв «children».
2. Дана строка символов, среди которых есть хотя бы одна точка. Преобразовать строку, удалив из неё все запятые, предшествующие первой точке.
3. Составить программу упорядочивания слов по алфавиту. Множество слов
представлено в виде строки символов заданного размера. Слова в строке отделены символом пробел.
4. Багаж пассажира характеризуется количеством вещей и общим весом вещей. Дан массив, содержащий информацию о багаже нескольких пассажиров.
Определить, имеются ли два пассажира, багажи которых совпадают по числу вещей и различаются по весу не более чем на 0,5 кг.
5. Сведения о служащих содержат фамилию, адрес, дату приема на работу,
годовой заработок и номер отдела. Вывести данные о служащих, работающих в
отделе №5.
Вариант 5
1. Даны натуральное число n, символы s1, …, sn. Заменить в этой последовательности все символы «a» на символ «e».
2. Дана строка символов, среди которых есть хотя бы одна точка. Преобразовать строку, удалив из нее все знаки « + ».
3. Составить программу определения подстроки максимального размера, которая входит в две заданные строки указанного размера.
4. Сведения об ученике состоят из его имени, фамилии и названия класса
(года обучения и буквы), в котором он учится. Дан массив, содержащий сведения
об учениках школы. Выяснить, имеются ли в школе, ученики с фамилией «Иванов».
5. Сведения о служащих содержат фамилию, адрес, дату приема на работу,
годовой заработок и номер отдела. Вывести данные о служащих, принятых на работу после 4 января 1990 года.
51
49.
Вариант 61. Даны натуральное n, символы s1, …, sn. Определить число вхождений в
последовательность s1, …, sn группы букв «abc».
2. Дана строка символов. Известно, что среди символов строки имеется хотя
бы один символ, отличный от пробела. Преобразовать строку, удалив группы
пробелов, которыми начинается и заканчивается строка. Если указанных групп
пробелов нет, то оставить строку без изменения.
3. Составить программу преобразования строки символов во множество
слов. Слово в строке выделяется по символу-ограничителю.
4. Сведения об ученике состоят из его имени, фамилии и названия класса
(года обучения и буквы), в котором он учится. Дан массив, содержащий сведения
об учениках школы. Выяснить, имеются ли однофамильцы в каких-либо параллельных классах.
5. Сведения о служащем содержат фамилию, адрес, дату приема на работу,
годовой заработок и номер отдела. Подсчитать количество служащих в каждом
отделе и их средний годовой заработок.
Вариант 7
1. Даны натуральное n, символы s1, …, sn. Определить число вхождений в
последовательность s1, …, sn группы символов «ef».
2. Дана строка символов. Известно, что среди символов строки имеется хотя
бы один символ, отличный от пробела. Преобразовать строку, заменив каждую
группу внутренних пробелов одним пробелом. Если указанных групп пробелов
нет, то оставить строку без изменения.
3. Составить программу подсчета числа подстрок в строке символов заданного размера. Подстроки выделяются по символу-ограничителю.
4. Сведения об ученике состоят из имени и фамилии и названия класса (года
обучения и буквы), в котором он учится. Дан массив, содержащий сведения об
учениках школы. Выяснить, имеются ли однофамильцы в каком-либо классе.
5. Багаж пассажира характеризуется количеством вещей и их общим весом.
Дан массив, содержащий информацию о багаже нескольких пассажиров. Найти
число пассажиров, имеющих более двух вещей и число пассажиров, количество
вещей которых превосходит среднее число вещей.
Вариант 8
1. Даны натуральное число n, символы s1, …, sn. Исключить из последовательности s1, …, sn группы символов, расположенные между круглыми скобками.
Сами скобки тоже должны быть исключены. Предполагается, что внутри каждой
пары скобок нет других скобок.
2. Дана строка символов. Преобразовать строку следующим образом: если
нет символа « », то оставить ее без изменения, иначе заменить каждый символ,
52
50.
встречающийся после первого вхождения символа « », на символ «/».3. Составить программу выделения из заданной строки множества различных слов. Определить частоту повторения каждого слова в строке. Результирующее множество представляется в виде строки символов. Слова в строке отделяются символом пробел.
4. Сведения об ученике состоят из его имени, фамилии и названия класса
(года обучения и буквы), в котором он учится. Дан массив, содержащий сведения
об учениках школы. Выяснить, имеются ли в школе ученики, у которых совпадают имя и фамилия.
5. Багаж пассажира характеризуется количеством вещей и их общим весом.
Дан массив, содержащий информацию о багаже нескольких пассажиров. Найти
багаж, средний вес одной вещи в котором отличается не более чем на 0,3 кг от
общего среднего веса всех вещей.
Вариант 9
1. Даны натуральное n, символы s1, …, sn. Подсчитать наибольшее количество идущих подряд пробелов.
2. Дана строка символов. Группы символов, разделенные одним или несколькими пробелами и не содержащие пробелы внутри себя, будем называть
словами. Подсчитать количество букв «a» в последнем слове данной строки.
3. Составить программу нормализации строки символов путем исключения
из нее всех идущих подряд одинаковых символов. Вместо них вставить один символ.
4. Сведения об ученике состоят из его имени, фамилии и названия класса
(года обучения и буквы), в котором он учится. Дан массив, содержаний сведения
об учениках школы. Получить список учеников каждого класса.
5. Даны сведения об учащихся: шифр класса, шифр дисциплины, количество
отличных оценок, количество хороших оценок, количество удовлетворительных и
неудовлетворительных оценок, пропущено лекций, пропущено практических занятий. Вывести исходные данные в виде табл. 1.2.
Таблица 1.2
Класс
Пропущено
занятий
Отличных
1
2
3
Итого:
53
Количество оценок
Хороших
Удовл.
Неуд.
51.
Вариант 101. Даны символы s1, s2, … Известно, что символ s1 отличен от восклицательного знака, и что среди s2, s3, … есть по крайней мере один восклицательный знак.
Пусть s1, …, sn — символы данной последовательности, предшествующие первому восклицательному знаку (n заранее не известно). Определить количество пробелов среди s1, …, sn.
2. Дана строка символов. Группы символов, разделенные одним или несколькими пробелами и не содержащие пробелов внутри себя, назовем словами.
Найти самое длинное слово в строке среди слов, вторая буква которых «e»; если
слов с наибольшей длиной несколько, то найти последнее. Если таких слов нет, то
сообщить об этом. Решить задачу, полагая, что слова состоят не более чем из 10
символов.
3. Составить программу извлечения слова из множества слов по порядковому номеру. Множество слов представлено в виде строки символов заданного
размера. В строке слова отделены символом пробела.
4. Сведения об ученике состоят из его имени, фамилии, названия класса (года обучения и буквы) и отметки, полученные в последней четверти. Дан массив,
содержащий сведения об учениках школы. Выяснить, сколько учеников школы не
имеют отметок ниже «хорошо». Напечатать фамилии учеников, класс, в котором
они учатся и общее количество таких учеников.
5. Даны сведения об учащихся: шифр класса, шифр дисциплины, количество
отличных оценок, количество хороших оценок, количество удовлетворительных и
неудовлетворительных оценок, пропущено лекций, пропущено практических занятий. Вывести данные в виде табл. 1.3.
Таблица 1.3
Класс
Пропущено
занятий
Отличных
Количество оценок
Хороших
Удовл.
Неуд.
1
2
3
Итого:
Вариант 11
1. Даны символы s1, s2, … Известно, что символ s1 отличен от восклицательного знака и что среди s2, s3, … есть по крайней мере один восклицательный знак.
Пусть s1, …, sn — символы данной последовательности, предшествующие первому восклицательному знаку (n заранее не известно). Выяснить, верно ли, что среди s1, …, sn имеются все буквы, входящие в слово «шина».
2. Даны две строки f и g. Записать в строку h все начальные совпадающие
54
52.
символы строк f и g.3. Составить программу поиска слова минимальной длины. Множество слов
представляется в виде строки символов заданного размера. Слова разделены символом пробел.
4. Сведения об ученике состоят из его имени, фамилии, названия класса (года обучения и буквы) и отметок, полученных в последней четверти. Дан массив,
содержащий сведения об учениках школы. Напечатать сведения о лучших учениках школы, то есть об учениках, не имеющих отметок ниже «хорошо» и по сумме
баллов не уступающих другим ученикам своего и параллельных классов.
5. Даны сведения об учащихся: шифр класса, шифр дисциплины, количество
отличных оценок, количество хороших оценок, количество удовлетворительных и
неудовлетворительных оценок, количество пропущенных лекций, количество
пропущенных практических занятий. Вывести входные данные в виде табл. 1.4.
Таблица 1.4
Шифр Средний
дисципбалл
лины
Всего
Пропущено занятий
В том числе
Лекций
Практических
Вариант 12
1. Даны символы s1, s2, … Известно, что символ s1 отличен от восклицательного знака и что среди s2, s3, … есть по крайней мере один восклицательный знак.
Пусть s1, …, sn — символы данной последовательности, предшествующие первому восклицательному знаку (n заранее не известно). Выяснить, входит ли в последовательность s1, …, sn буква «t».
2. Дана строка символов. Группы символов, разделенные одним или несколькими пробелами и не содержащие пробелов внутри себя, будем называть
словами. Удалить из строки все однобуквенные слова и лишние пробелы.
3. Составить программу замены слова в строке заданного размера. Местоположение заменяемого слова заранее не известно. Слова в строке отделены символом пробел.
4. Сведения об автомобиле состоят из его марки, номера и фамилии владельца. Дан массив, содержащий сведения о нескольких автомобилях. Найти количество автомобилей каждой марки.
5. Даны сведения об учащихся: шифр класса, шифр дисциплины, количество
отличных оценок, количество хороших оценок, количество удовлетворительных и
неудовлетворительных оценок, количество пропущенных лекций, количество
пропущенных практических занятий. Вывести входные данные в виде табл. 1.5.
55
53.
Таблица 1.5Шифр
дисциплины
Средний
балл
Количество оценок
Отличных Хороших Удовлетв.
Неуд.
Вариант 13
1. Даны натуральное число n, символы s1, …, sn. Преобразовать последовательность s1, …, sn заменив в ней каждую точку многоточием.
2. Дан текст, каждый символ которого может быть буквой, цифрой или одним из знаков «+», «-», « ». Группой букв будем называть такую совокупность
последовательно расположенных букв, которой непосредственно не предшествует
и за которой непосредственно не следует буква. Выяснить, встречается ли в данном тексте группа букв «one».
3. Составить программу сортировки слов в множестве по возрастанию их
длины. Множество слов представлено в виде строки символов. Слова в строке отделены символом пробел.
4. Дан массив, содержащий различные даты. Каждая дата — это число, название месяца и год. Найти год с наименьшим номером.
5. Даны сведения об учащихся: шифр класса, шифр дисциплины, количество
отличных оценок, количество хороших оценок, количество удовлетворительных и
неудовлетворительных оценок, количество пропущенных лекций, количество
пропущенных практических занятий. Вывести входные данные в виде табл. 1.6.
Таблица 1.6
Шифр
группы
Средний балл
Количество оценок
Отличных Хороших
Удовл.
Неуд.
Вариант 14
1. Даны натуральное число n, символы s1, …, sn. Преобразовать последовательность s1, …, sn, заменив в ней каждую группу стоящих рядом точек одной
точкой.
2. Дан текст. Группы символов, разделенные пробелом (одним или несколькими) и не содержащие пробелы внутри себя, будем называть словами. В тех словах, которые оканчиваются сочетанием букв «ing», заменить это окончание на
56
54.
«ed».3. Составить программу упорядочения слов в множестве слов по алфавиту.
Множество слов представлено в виде строки символов заданного размера. Слова в
строке отделены символом пробел.
4. Дан массив, содержащий различные даты. Каждая дата — это число, название месяца, год. Найти все весенние даты.
5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
стаж работы, разряд рабочего, номер цеха, номер участка, сумма заработной платы. Вывести на печать входные данные в виде табл. 1.7.
Таблица 1.7
№ участка
Количество
рабочих
Средняя заработная плата
В том числе по разрядам
1
2
3
Всего
Вариант 15
1. Даны натуральное число n, символы s1, …, sn. Преобразовать последовательность s1, …, sn, заменив в ней каждую из групп стоящих рядом точек многоточием.
2. Дан текст. Группы символов, разделенные пробелом (одним или несколькими) и не содержащие пробелы внутри себя, назовем словами. Для каждого из
слов указать, сколько раз оно встречается.
3. Составить программу выделения подстроки максимальной длины, которая встречается более одного раза.
4. Дан массив, содержащий различные даты. Каждая дата — это число, название месяца и год. Найти самую позднюю дату.
5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
стаж работы, разряд рабочего, номер цеха, номер участка, сумма заработной платы. Вывести на экран табл. 1.8.
Таблица 1.8
Цеха
Количество рабочих
Всего
В том числе
Мужчин
Женщин
57
Средняя заработная плата
В том числе
Всего
Мужчин Женщин
55.
Вариант 161. Даны натуральное число n, символы s1, …, sn. Выяснить, имеются ли в последовательности s1, …, sn такие члены последовательности si, si+1, что si — это
запятая, а si+1 — тире.
2. Дан текст. Группы символов, разделенные одним или несколькими пробелами и не содержащие пробелов внутри себя, назовем словами. Найти все слова, содержащие наибольшее количество латинских букв «a», «e», «i».
3. Составить программу сдвига подстроки размером n в строке символов
длины m ( n m ) на заданное число символов. Символы, выходящие за пределы
строки, теряются. Освободившиеся места заполняются пробелами.
4. Дан массив, содержащий сведения о книгах. Сведения о каждой книге —
это фамилия автора, название и год издания. Найти названия книг данного автора,
изданных с 1960 года.
5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
стаж работы, разряд рабочего, номер цеха, номер участка, сумма заработной платы. Вывести на экран табл. 1.9.
Таблица 1.9
№ участка
Всего
Количество рабочих
В том числе по разрядам
1
2
3
Вариант 17
1. Даны натуральное число n, символы s1, …, sn. Получить первое натуральное i, для которого каждый из символов si и si+1 совпадает с буквой «a». Если такой пары нет, то ответом должно быть число 0.
2. Дан текст. Группы символов, разделенные одним или несколькими пробелами и не содержащие пробелы внутри себя, назовем словами. Найти все слова,
в которых доля букв «а», «b» максимальна.
3. Составить программу сжатия строки заданной длины с указанного места
на заданное число символов. При сжатии сдвигается правая часть строки.
4. Дан массив, содержащий сведения о книгах. Сведения о каждой книге содержат фамилию автора, название и год издания. Определить, имеется ли книга с
названием «Информатика». Если да, то сообщить фамилию автора и год издания.
Если таких книг нет, то сообщить об этом. Если таких книг несколько, то сооб58
56.
щить сведения о всех книгах.5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
стаж работы, разряд рабочего, номер цеха, номер участка, сумма заработной платы. Вывести входные данные в виде табл. 1.10.
Таблица 1.10
№ участка
Средняя
б
Количество рабочих
В том числе по разрядам
1
2
3
Всего
Вариант 18
1. Даны натуральное число n, символы s1, …, sn. Известно, что среди
s1, …, sn есть по крайней мере одна запятая. Найти такое натуральное i, что si —
первая запятая.
2. Дан текст. Группы символов, разделенные одним или несколькими пробелами и не содержащие внутри себя пробелов, назовем словами. Для каждого из
слов указать, сколько раз оно встречается в тексте.
3. Составить программу замены слова в строке заданного размера. Местоположение заменяемого слова изначально не известно. Слова в строке отделены
символом пробел.
4. Дан массив, содержащий сведения о книгах. Сведения о каждой из
книг — это фамилия автора, название и год издания. Определить книги, изданные
за период с 1970 па 1990 годы. Если таких книг нет, то сообщить об этом.
5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
стаж работы, разряд рабочего, номер цеха, номер участка, сумма заработной платы. Вывести входные данные в виде табл. 1.11.
Таблица 1.11
№ цеха
Количество рабочих
В том числе
Всего
Мужчин Женщин
59
Количество рабочих, %
В том числе
Всего
Мужчин Женщин
57.
Вариант 191. Даны натуральное число n, символы s1, …, sn. Подсчитать, сколько раз
среди данных символов встречается буква «x».
2. Дан текст, каждый символ которого может быть малой буквой, цифрой
или одним из знаков «+», «-», « ». Группой букв назовем такую совокупность последовательно расположенных букв, которой непосредственно не предшествует и
за которой непосредственно не следует буква. Найти число тех групп букв, которые не заканчиваются той же буквой, что и первая группа букв.
3. Составить программу раздвижки строки заданного размера с указанного
места на заданное число символов. При раздвижке сдвигается правая часть строки. Освободившееся место заполняется пробелами.
4. Дан массив, содержащий номера телефонов сотрудников учреждения:
указывается фамилия сотрудника, его инициалы и номер телефона. Найти телефон сотрудника по его фамилии и инициалам.
5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
стаж работы, разряд рабочего, номер цеха, номер участка, сумма заработной платы. Вывести на печать входные данные в виде табл. 1.12.
Таблица 1.12
№ цеха
Всего
Средняя заработная плата
в том числе по разрядам
1
2
3
1
2
3
Вариант 20
1. Даны натуральное число n, символы s1, …, sn. Известно, что среди
s1, …, sn есть по крайней мере одна запятая. Найти такое натуральное i, что si —
последняя по порядку запятая.
2. Дана строка символов. Группы символов, разделенных одним или несколькими пробелами и не содержащие пробелов внутри себя, назовем словами.
Считая, что количество символов в слове не превосходит 10, определить, сколько
в строке имеется слов, состоящих из одного, двух и трех символов.
3. Составить программу сцепления двух строк заданного размера.
4. Дан массив, содержащий сведения о кубиках: размер каждого кубика
(длина ребра в см), его цвет (красный, желтый, зеленый или синий) и материал
(деревянный, металлический, картонный). Найти количество кубиков каждого из
перечисленных цветов и их суммарный объем.
5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
60
58.
стаж работы, разряд рабочего, номер цеха, номер участка, сумма заработной платы. Вывести на печать входные данные в виде табл. 1.13.Таблица 1.13
№ цеха
Количество рабочих
По стажу работы, лет
Всего
До 6
6—10
11—15
16—20
Свыше
20
Вариант 21
1. Даны натуральное число n, символы s1, …, s20. Подсчитать, сколько раз
среди данных символов встречается символ «+» и сколько раз символ « ».
2. Дан текст, каждый символ которого может быть буквой, цифрой или одним из знаков «+», «-», « ». Группой цифр будем называть такую совокупность
последовательно расположенных цифр, которой непосредственно не предшествует и за которой непосредственно не следует цифра. Найти самую длинную группу
цифр. Если наибольшую длину имеет несколько групп, то взять первую по порядку.
3. Составить программу поиска всех вхождений строки символов заданного
размера n в строку символов размером m ( n m ).
4. Дан массив, содержаний сведения о кубиках: размер каждого кубика
(длина ребра в см), его цвет (красный, желтый, зеленый или синий) и материал
(деревянный, металлический или картонный). Найти количество деревянных кубиков с ребром 3 см и количество металлических кубиков с ребром, большим 5
см.
5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
стаж работы, разряд рабочего, № цеха, № участка, сумма заработной платы. Вывести на печать табл. 1.14.
Таблица 1.14
Стаж работы
(лет)
До 6
С 6 до 11
С 11 до 16
Свыше 16
Всего
Средняя заработная плата
В том числе по разрядам
1
2
3
61
59.
Вариант 221. Даны натуральное число n, символы s1, …, sn. Подсчитать, общее число
вхождений символов «+», «-», « » в последовательность s1, …, sn.
2. Дан текст, каждый символ которого может быть буквой, цифрой или одним из знаков «+», «-», « ». Группой букв будем называть совокупность последовательно расположенных букв, которой непосредственно не предшествует и за
которой непосредственно не следует буква. Подсчитать число таких групп букв,
которые начинаются и кончаются одной и той же буквой.
3. Составить программу определения лексикографического порядка (следования по алфавиту) двух строк заданного размера. Строки могут быть различной
длины.
4. Дан массив, содержащий сведения о веществах: указывается название вещества, его удельный вес и проводимость (проводник, полупроводник, изолятор).
Найти удельные веса и названия всех полупроводников.
5. Даны сведения о рабочих: табельный номер, Ф.И.О., год рождения, пол,
стаж работы, разряд рабочего, номер цеха, номер участка, сумма заработной платы. Вывести на печать входные данные в виде табл. 1.15.
Таблица 1.15
Стаж работы, лет
Всего
Количество рабочих
в том числе по разрядам
1
2
3
До 6
С 6 до 11
С 11 до 16
С 16 до 21
Свыше 21
Вариант 23
1. Даны натуральное число n, символы s1, …, sn. Преобразовать последовательность s1, …, sn, заменив на «ks» первое вхождение буквы «x», если такое есть.
2. Дана строка символов. Известно, что первый символ строки s1 отличен от
пробела и что среди s2, s3, … имеется хотя бы один пробел. Преобразовать подстроку символов s1, …, sn, предшествующую первому пробелу (n заранее не известно), удалив из неё все символы, не являющиеся буквами.
3. Составить программу поиска слова максимальной длины в множестве
слов. Множество слов представлено в виде строки символов заданного размера.
Слова отделены символом пробел.
4. Дан массив, содержащий сведения о веществах: указывается название вещества, его удельный вес и проводимость (проводник, полупроводник, изолятор).
62
60.
Выбрать данные о проводниках и упорядочить их по убыванию удельных весов.5. Даны сведения за месяц о пропусках занятий студентами групп. Структура записи: шифр группы, фамилия, пропущено часов, оправдано часов. Подсчитать количество неоправданных часов по каждому студенту, суммарные показатели по каждому виду, а также процент неоправданных пропусков в целом.
Вариант 24
1. Даны натуральное n, символы s1, …, sn. Преобразовать последовательность s1, …, sn, удалив первое вхождение «W», если такое есть. Образовавшуюся
«дыру» заполнить последующими буквами, а в конец добавить пробел.
2. Дана строка символов. Известно, что первый символ строки s1 отличен от
пробела и что среди s2, s3, … имеется хотя бы один пробел. Преобразовать подстроку символов s1, …, sn (n заранее не известно), удалив из каждой группы идущих подряд цифр, в которой более двух цифр и которой не предшествует точка,
все цифры, начиная с третьей (например, «ab+0.173-1.1» преобразуется в
«ab+0.17-1.1»).
3. Составить программу выделения подстроки в строке, которая повторяется
максимальное число раз.
4. Дан массив, содержащий сведения об экспортируемых товарах: указывается наименование товара, страна, импортирующая товар, и объем поставляемой
партии в штуках. Найти страны, в которые экспортируется данный товар и общий
объем его экспорта.
5. Даны сведения об использовании машинного времени на ВЦ кафедрами
института. Структура записи: код кафедры, название кафедры, расход машинного
времени: по плану, фактически. Определить отклонения по расходу машинного
времени по каждой кафедре, суммарные показатели планового и фактического
расхода машинного времени в целом по институту и дать заключение: превшен
или нет плановый фонд машинного времени. Результаты представить в абсолютных цифрах, а итоговую разность — в абсолютном выражении (со знаком) и в
процентах. Результаты оформить в виде таблицы.
Вариант 25
1. Даны натуральное число n и символы s1, …, sn, среди которых есть двоеточие. Получить все символы, расположенные между первым и вторым двоеточием. Если второго двоеточия нет, то получить все символы, расположенные после
единственного двоеточия.
2. Дана строка символов. Группы символов, разделенные одним или несколькими пробелами и не содержащие пробелы внутри себя, будем называть
словами. Найти количество слов, начинающихся с буквы «c».
3. Составить программу выделения символов, из которых состоит строка заданного размера. Подсчитать частоту появления каждого символа в строке.
4. Дан массив, содержащий сведения об игрушках: указывается название иг63
61.
рушки, её стоимость в копейках и возрастные границы детей, для которых онапредназначена (например, для детей от 2 до 5 дет). Получить названия игрушек,
цена которых не превышает 400 руб. и которые подходят детям 5 лет.
5. Даны сведения о времени выполнения заданий на ЭВМ. Структура записи: шифр задания, код отдела, Ф.И.О. программиста, общее время прохождения
задания tзадан, время центрального процессора tцп (tзадан>tцп). Получить процент
процессорного времени по каждому заданию, а также суммы по видам времени по
всем заданиям и средний процент времени центрального процессора по всем заданиям. Результаты оформить в виде таблицы.
64





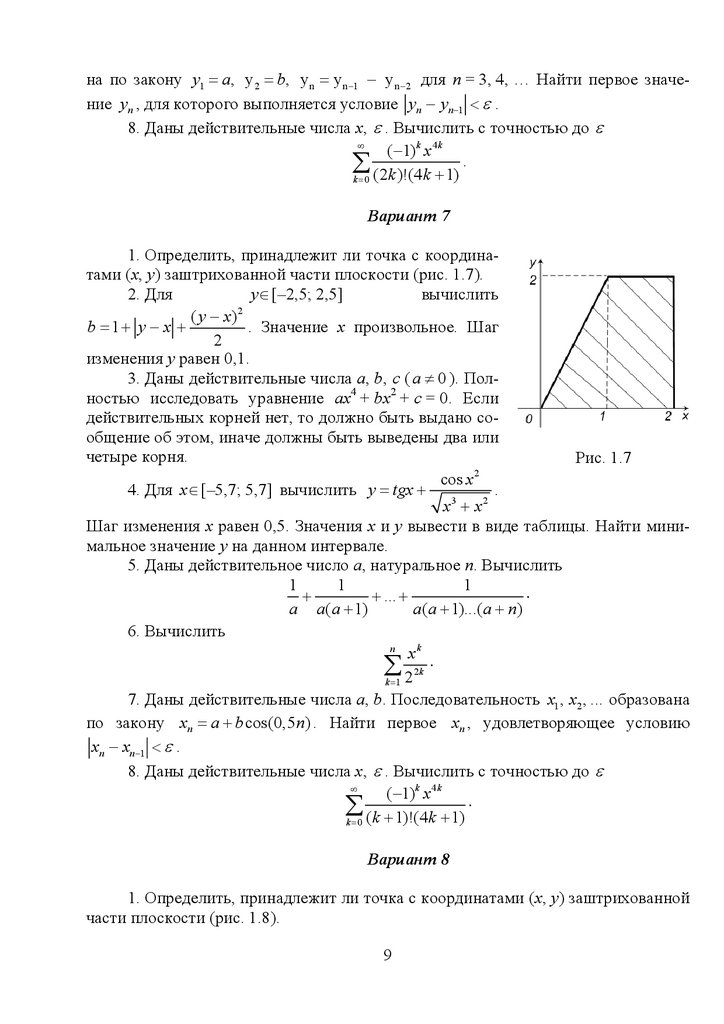















































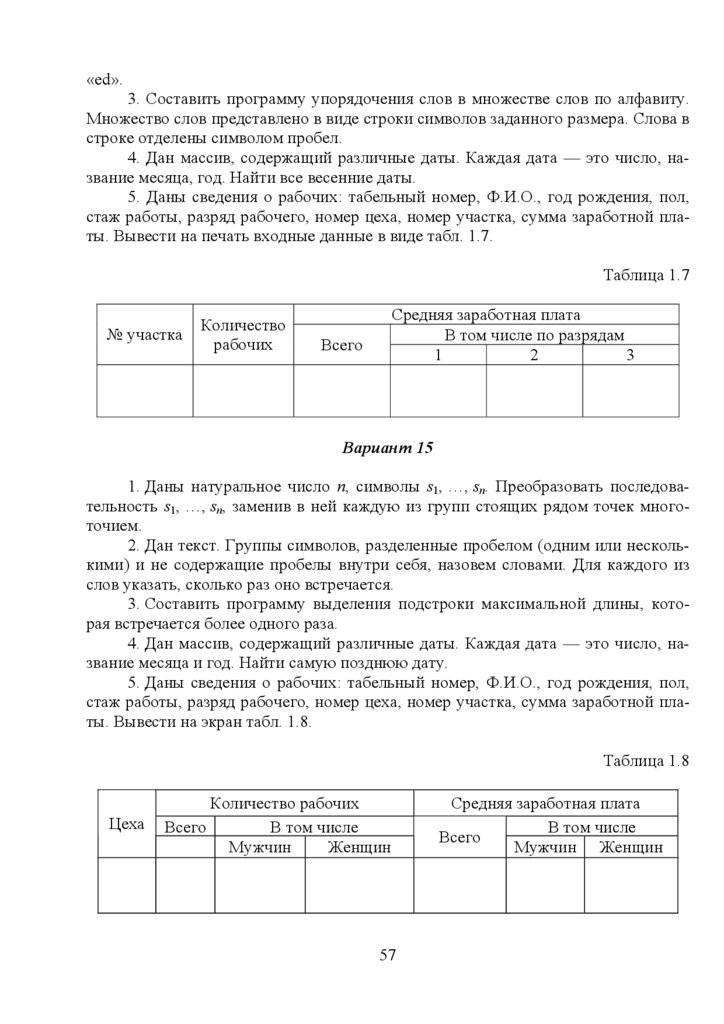







 programming
programming








