Similar presentations:
Элементы теории погрешности и математическая обработка результатов наблюдений. Часть 1
1.
Кафедра: ПДС и МЭЛЕМЕНТЫ ТЕОРИИ
ПОГРЕШНОСТИ И
МАТЕМАТИЧЕСКАЯ
ОБРАБОТКА РЕЗУЛЬТАТОВ
НАБЛЮДЕНИЙ
2.
Содержание• Классификация погрешностей.
• Оценка инструментальной погрешности по
классу точности, средств измерений.
• Оценка случайной составляющей погрешности
результата наблюдений и результата измерений
средств измерений.
• Исключение систематической погрешности
результата измерений.
• Оценка погрешности косвенных измерений.
• Формы представления результата измерений.
3.
Погрешность(неопределённость) отклонение результата
измерения Ах от истинного
значения А:
Δ = Ax - A
A – истинное значение значение физической
величины, которое идеальным
образом характеризует в
качественном и
количественном отношении
соответствующую физическую
величину;
Ax – результат измерения.
4.
На практике:Δ = Ax - Aо
Aо – действительное
значение:
значение физической
величины, полученное
экспериментальным путем и
настолько близкое к
истинному значению, что в
поставленной измерительной
задаче может быть
использовано вместо него.
5.
Классификацияпогрешностей.
1.
2.
3.
4.
по характеру проявления;
по источнику возникновения;
по условиям применения;
по характеру поведения
измеряемой величины в процессе
измерения;
5. по закономерности зависимости от
размера измеряемой величины;
6. по способу выражения.
6.
1. По характеру проявления:1.1. систематическая,
1.2. случайные,
1.3. грубые.
7.
2. По источнику возникновения:2.1. погрешность метода измерений,
2.2. инструментальная погрешность,
2.3. субъективная погрешность.
8.
3. По условиям применения1) основная,
2) дополнительная.
9.
4. По характеру поведения измеряемойвеличины в процессе измерения
1) статическая – Δ стат
2) в динамическом режиме–
Δ динам.реж.
3) динамическая
Δ динам. = Δ динам.реж. − Δ стат
10.
5. По закономерности зависимости отразмера измеряемой величины
5.1. Аддитивные.
5.2. Мультипликативные .
11.
6. По способу выражения6.1. Абсолютная
Ax A0 [ед. измерения]
Ax -измеренное значение
A0 -действительное
значение
12.
6. По способу выражения6.2. Относительная
A0
100
Ax
100 %
13.
6. По способу выражения6.3.
Приведенная
100%
Aн
Aн – нормирующее значение (может
быть равным конечному значению
шкалы, либо – ее геометрической длине
,либо – диапазону измерения, либо –
произвольным).
14.
Относительную погрешностьчасто выражают в %.
A0
100
Точность измерений
Например,
Ax
100 %
q
1
0.1%, q 1000
,
15.
Оценкаинструментальной
погрешности по
классу точности,
средств измерений.
16.
Оценка инструментальной погрешности поклассу точности, средств измерений.
Инструментальную погрешность
нормируют путем указания пределов
допускаемой погрешности.
пред . пред .
пред–. наибольшая по модулю
погрешность средства измерения,
при которой оно еще может быть
допущено к применению.
17.
Формы представления пределовдопускаемой погрешности.
1. в форме абсолютной погрешности;
2. в форме относительной погрешности;
3. в форме приведенной погрешности.
18.
1. В форме абсолютной погрешности.2. В форме относительной
погрешности.
2.1 Обозначение: ©
где
с
число из «ряда»:
n
(1; 1,5; 2; 2,5; 4; 5; 6) × 10 ,
где n = 1, 0, -1, -2...
пред . c [%]
сА
n
пред
100
19.
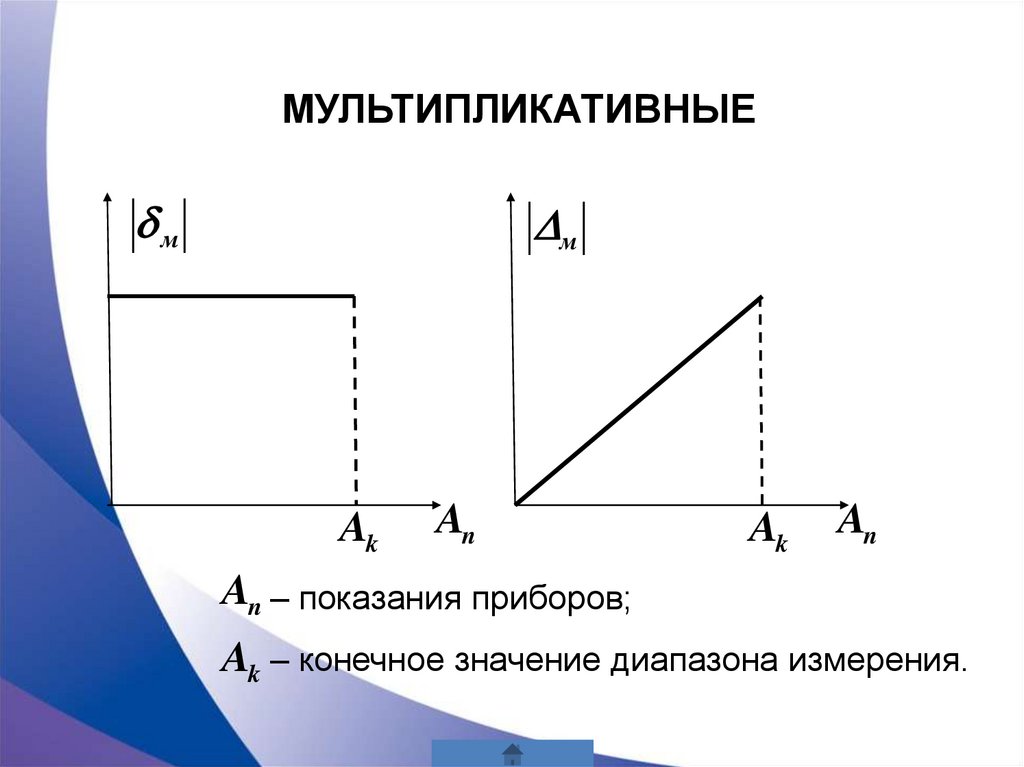
МУЛЬТИПЛИКАТИВНЫЕм
м
Ak
An
Ak
An
An – показания приборов;
Ak – конечное значение диапазона измерения.
20.
2.2Обозначение: c / d
где c и d числа из «ряда»,
(указанного в пункте 2.1)
k
пред . c d
1
n
k – наибольший по модулю из
n
диапазона измерения,
– показание прибора.
21.
3. В форме приведеннойпогрешности
3.1 Обозначение
- число из «ряда»:
(указанного в
пред.
Aн
100
Aн ,
пункте 2.1)
Aн
пред .
[%]
Aп
– нормирующее значение.
22.
Aн – нормирующее значение, которое может бытьравно:
а) Aн Aк
, если нулевая отметка
находится на краю шкалы;
б) Aн Aк1 Aк2
, если нулевая
отметка находится внутри шкалы
в) Aн Aк1 Aк2
, если прибор с
условным нулем (нулевая отметка вне
пределов шкалы),
где Aк , Aк 1 и Aк 2 – конечные значения
шкалы прибора.
23.
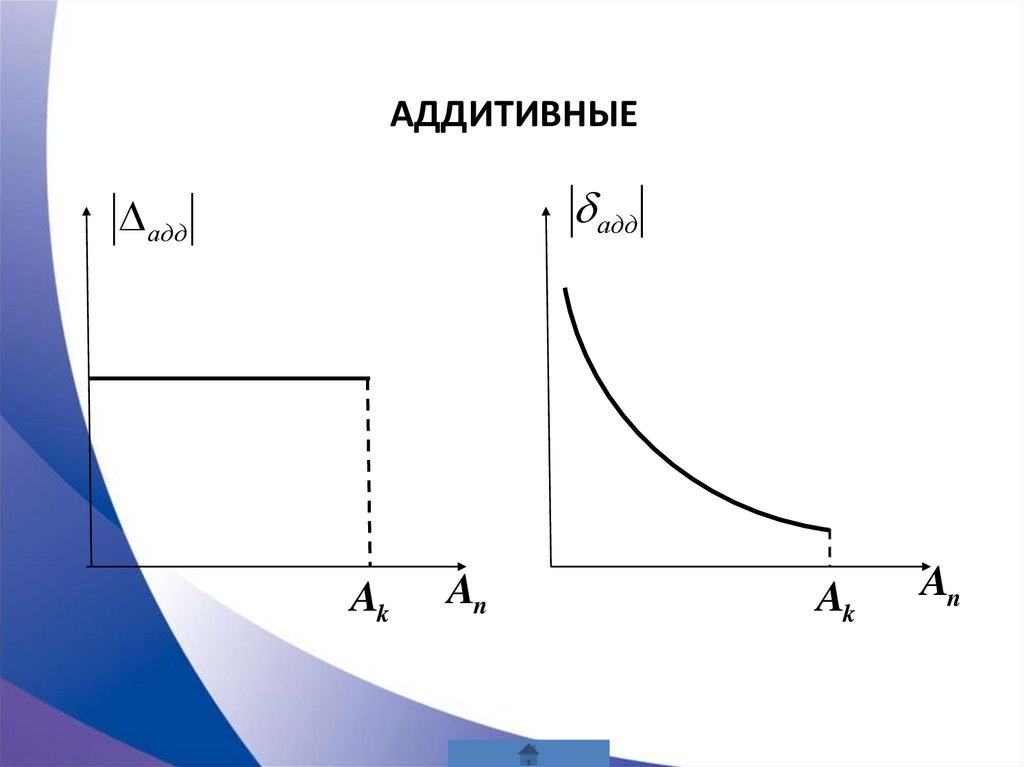
АДДИТИВНЫЕадд
адд
Ak
An
Ak
An
24.
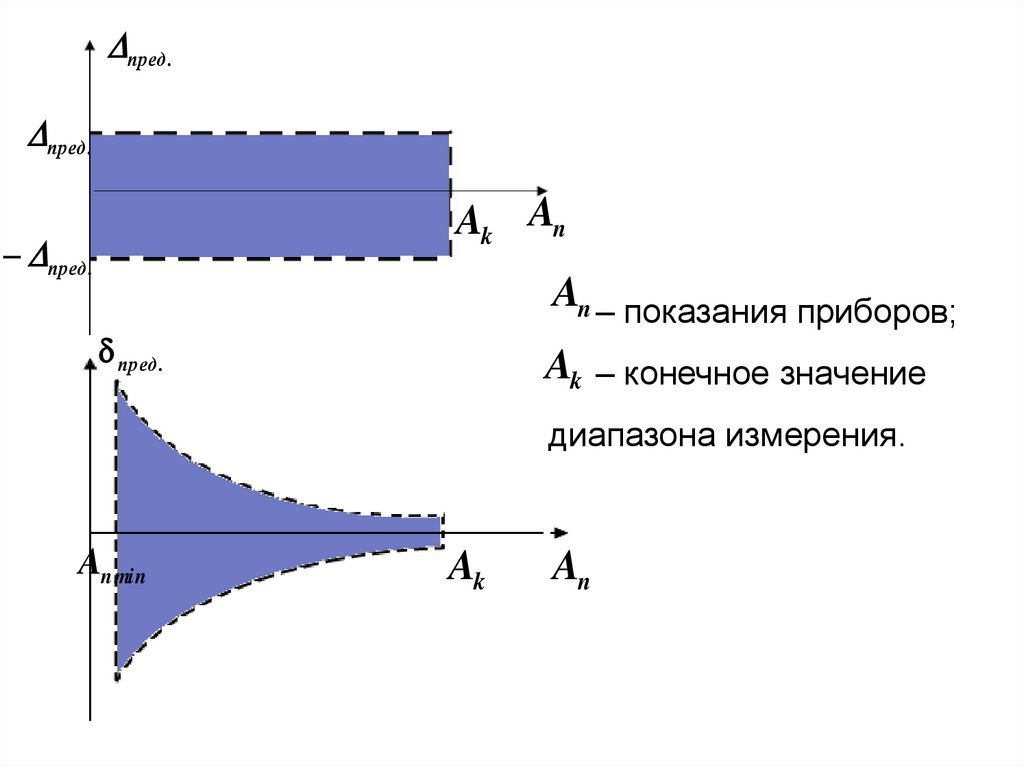
пред .пред .
Ak An
пред .
An – показания приборов;
пред .
Ak – конечное значение
диапазона измерения.
An min
Ak
An





















 mathematics
mathematics








