Алгоритмы и структуры данных. Практика №1 (3 модуль). Ленточная стратегия

1.

Алгоритмы и структуры
данных
практические занятия
Марквирер Владлена Дмитриевна
[email protected]

2.

Онлайн курс
• Алгоритмы: теория и практика. Структуры данных
• Ссылка на курс на степике: https://stepik.org/course/1547/promo
• Срок прохождения: в течение 2-3 модуля
(примерно к концу марта 2023 года).
• Нужно пройти курс с оценкой не ниже 8 баллов для тех, кто хочет
получить высокую итоговую оценку (оценка за онлайн курс будет
учитываться в 3-4 модуле).
08.02.2023
НИУ ВШЭ - Пермь
2

3.

08.02.2023
НИУ ВШЭ - Пермь
3

4.

Формула
1. Сначала вычисляется накопленная оценка:
накоп = 0,3 * кр + 0,5 * семинары + 0,1 * online
⎻ если накопленная оценка устраивает, то экзамен можно не
сдавать (накоп = итог);
⎻ если накопленная не устраивает, то надо сдавать экзамен.
2. При сдаче экзамена:
итог = 0,25 * (кр + экз) + 0,4 * семинары + 0,1 * online
3. Можно получить 1 доп. балл за успешное выступление на личном
первенстве и краевой олимпиаде.
08.02.2023
НИУ ВШЭ - Пермь
4

5.

Практика №1 (3 модуль)
«Ленточная стратегия»

6.

Вторая модельная задача
(характеристики)
1.
2.
3.
4.
5.
6.
7.
8.
Количество заданий произвольно.
Каждое задание имеет свою длительность.
Задания независимы (можно выполнять одновременно).
Разрешены прерывания при выполнении задания, но нельзя
выполнять параллельно (в один момент времени) прерванные
задания.
Количество работников произвольно, но фиксировано.
Работники универсальны (каждый может выполнять любое задание).
Производительность работников, размеры оплаты труда и т.д. не
учитываются.
Требуется построить расписание выполнения всех заданий в
кратчайшие сроки.
08.02.2023
НИУ ВШЭ - Пермь
7

7.

«Ленточная» стратегия
«Ленточная» стратегия – является эффективным рекурсивным
алгоритмом для решения задач, относящихся ко второй модельной.
Дано:
n – независимых заданий
t1, t2, …, tn – длительности n заданий
k – количество универсальных исполнителей
Найти:
Оптимальное расписание для заданных заданий, их длительности и
заданного количества универсальных исполнителей.
08.02.2023
НИУ ВШЭ - Пермь
8

8.

«Ленточная» стратегия
Решение:
1. Найти оптимальное время по формуле:
2. Составляется «лента» из всех заданий.
3. Находится общая длительность всех заданий.
4. Исходная длина суммы длительностей в «ленте» делится на Tопт.
5. Далее полученные фрагменты распределяются между
исполнителями.
08.02.2023
НИУ ВШЭ - Пермь
9

9.

«Ленточная» стратегия (пример)
08.02.2023
НИУ ВШЭ - Пермь
10

10.

«Ленточная» стратегия (пример)
08.02.2023
НИУ ВШЭ - Пермь
11

11.

«Ленточная» стратегия (пример)
08.02.2023
НИУ ВШЭ - Пермь
12

12.

«Ленточная» стратегия
08.02.2023
НИУ ВШЭ - Пермь
13

13.

Ограничения
1. Необходимо помнить, что количество исполнителей не должно
быть меньше или равно 0.
2. Слишком много исполнителей использовать нецелесообразно –
рассмотреть вариант ввода ограничения на количество
исполнителей (бонусная задача).
3. Длительности и количество задач произвольное, также можно
поставить свои ограничения по типу данных для длительности (от
этого будет зависеть реализация, по умолчанию работаем с
целыми числами, при этом среднее значение всех длительностей
также берётся целочисленным, причём округлённое в большую
сторону).
08.02.2023
НИУ ВШЭ - Пермь
14

14.

Постановка задачи
Общая задача: реализовать эффективный алгоритм «ленточной» стратегии
для оптимизации составления расписания.
Основные требования:
⎻ работа в целых числах;
⎻ нет верхнего ограничения на количество исполнителей.
Бонусные требования:
⎻ работа с вещественными числами;
⎻ при вводе количества исполнителей выполняется предварительная
проверка допустимости по верхней границе в зависимости от
введённых задач и их длительности.
08.02.2023
НИУ ВШЭ - Пермь
15

15.

Практика №2 (3 модуль)
Конвейерная задача и уровневая
стратегия

16.

Первая модельная задача
(характеристики)
1. Количество заданий произвольно.
2. Каждое задание состоит из двух последовательных этапов, длительность
которых произвольна.
3. Задания независимы (можно выполнять одновременно).
4. Запрещены прерывания при выполнении задания.
5. Количество работников строго 2.
6. Первый работник выполняет только первый этап каждого задания, второй
работник – только второй этап каждого задания.
7. Производительность работников, размеры оплаты труда и т.д. не
учитываются.
8. Требуется построить расписание выполнения всех заданий в кратчайшие
сроки.
08.02.2023
НИУ ВШЭ - Пермь
17

17.

Почему называют «конвейерной»?
Выполнение второго этапа задания может начинаться только после
завершения первого этапа. Интерпретацию конвейерной задачи можно
описать так:
⎻ имеется набор деталей и два конвейера, на которых происходит
обработка деталей;
⎻ каждая деталь сначала попадает на первый конвейер, а затем на
второй;
⎻ время обработки каждой детали на каждом конвейере индивидуально;
⎻ порядок, в котором детали обрабатываются на первом конвейере,
может быть любым;
⎻ однако на втором конвейере порядок обработки деталей должен быть
таким же.
08.02.2023
НИУ ВШЭ - Пермь
18

18.

Алгоритм Джонсона
Эффективный (быстрый и точный) алгоритм для составления
кратчайшего расписания выполнения задач в два этапа.
Если имеется n задач, то возможных вариантов
последовательностей задач будет n!, что для больших n перебирать
не приемлемо.
08.02.2023
НИУ ВШЭ - Пермь
19

19.

Алгоритм Джонсона
Дано:
n – независимых заданий.
ai и bi – длительности первого и второго этапов i-го задания.
Исходные данные представляются в табличном виде.
Найти:
Кратчайшее расписание для заданных заданий и длительности их
этапов.
08.02.2023
НИУ ВШЭ - Пермь
20

20.

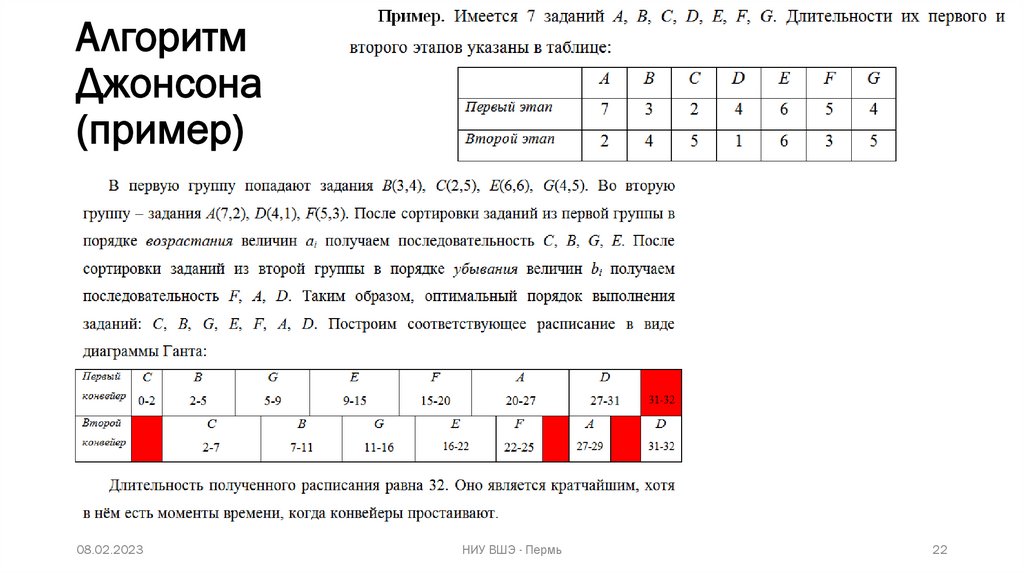
Алгоритм Джонсона
Решение:
1. Все задачи делятся на 2 группы:
⎻ в первой группе задачи, длительности которых ai ≤ bi ;
⎻ во второй – остальные (ai > bi ).
2. Задания в каждой группе сортируются:
⎻ в первой группе – по возрастанию ai;
⎻ во второй – по убыванию bi.
3. Далее составляется диаграмма Ганта с кратчайшим расписанием,
причём сначала выполняются все задачи из первой сортированной
группы, а затем – из второй сортированной. Нужно помнить, что
пока не закончится первый этап одной задачи – не может начаться
второй этап этой же задачи.
08.02.2023
НИУ ВШЭ - Пермь
21

21.

Алгоритм
Джонсона
(пример)
08.02.2023
НИУ ВШЭ - Пермь
22

22.

Третья модельная задача
(характеристики)
1. Количество заданий произвольно.
2. Все задания имеют одинаковую длительность (для удобства
длительность = 1)
3. Задания зависимы, причём граф зависимостей не имеет
транзитивных дуг.
4. Запрещены прерывания при выполнении задания.
5. Количество работников произвольно, но фиксировано.
6. Работники универсальны (каждый может выполнять любое задание).
7. Производительность работников, размеры оплаты труда и т.д. не
учитываются.
8. Требуется построить расписание выполнения всех заданий в
кратчайшие сроки.
08.02.2023
НИУ ВШЭ - Пермь
23

23.

Уровневая стратегия
Дано:
n – зависимых заданий.
m – количество идентичных исполнителей.
Исходные данные по зависимостям заданий представляются в
табличном виде.
Найти:
Кратчайшее расписание выполнения заданных заданий заданным
количеством исполнителей.
08.02.2023
НИУ ВШЭ - Пермь
24

24.

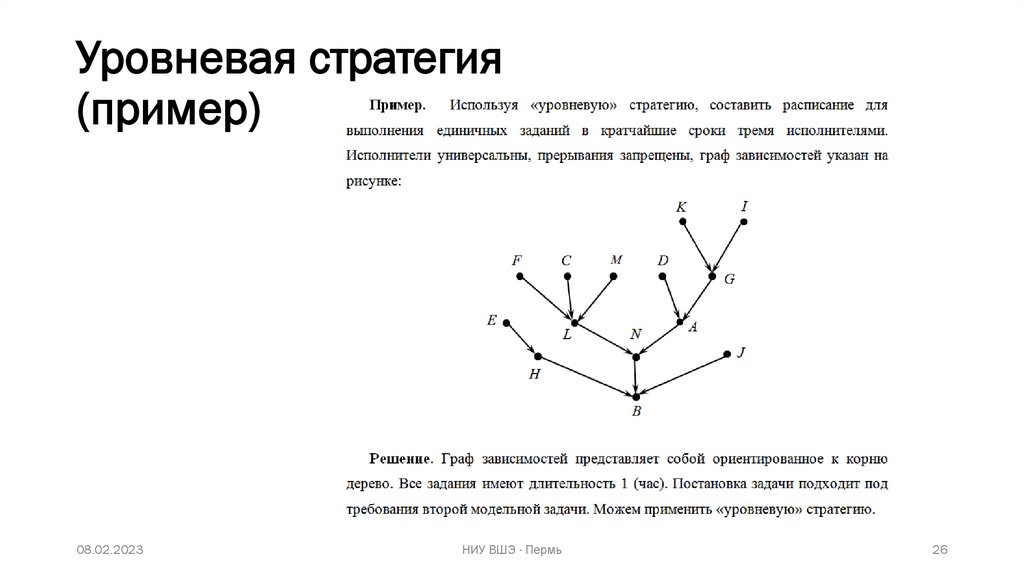
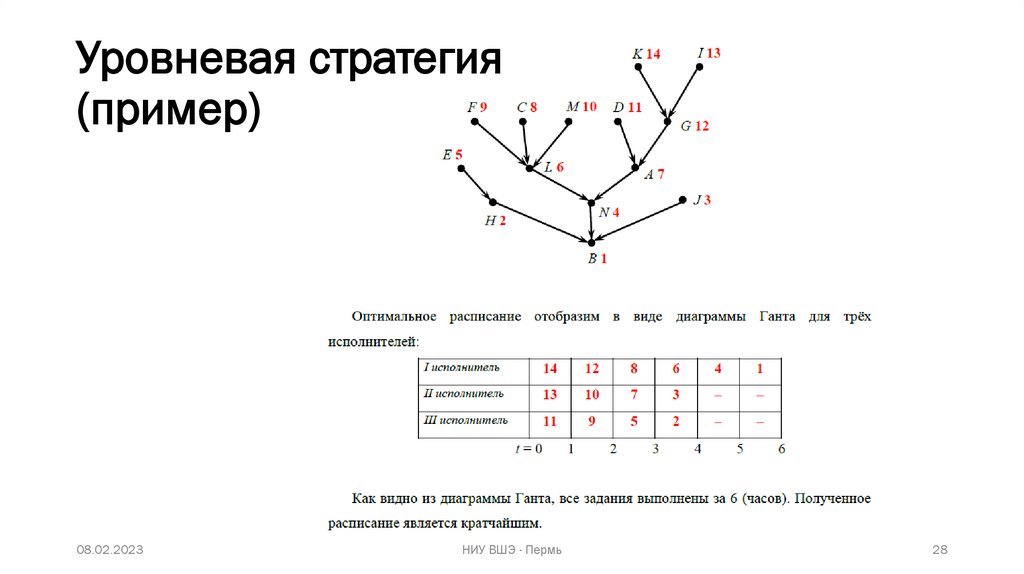
Уровневая стратегия
Решение:
1. Находится сток/стоки (нет выходящих дуг – нет последующих
заданий) дерева.
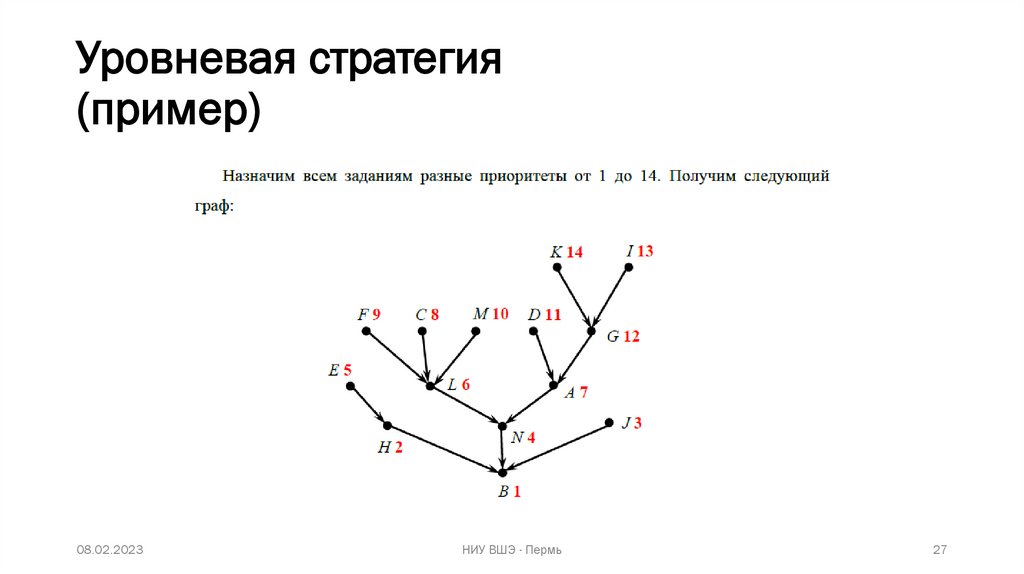
2. Выставляются приоритеты, начиная от 1 до k для найденных k
стоков.
3. Далее расставляются приоритеты для задач, начиная с той, у
которой прямой потомок имеет наименьший приоритет.
4. Затем составляется диаграмма Ганта, учитывая тот момент, что
при наличии незавершённых предшествующих задач, нельзя
выполнить текущую рассматриваемую задачу.
08.02.2023
НИУ ВШЭ - Пермь
25

25.

Уровневая стратегия
(пример)
08.02.2023
НИУ ВШЭ - Пермь
26

26.

Уровневая стратегия
(пример)
08.02.2023
НИУ ВШЭ - Пермь
27

27.

Уровневая стратегия
(пример)
08.02.2023
НИУ ВШЭ - Пермь
28

28.

Постановка задачи
1 задача: реализовать эффективный алгоритм Джонсона для
составления кратчайшего расписания конвейерной задачи.
2 задача: реализовать алгоритм уровневой стратегии для составления
кратчайшего расписания выполнения задач.
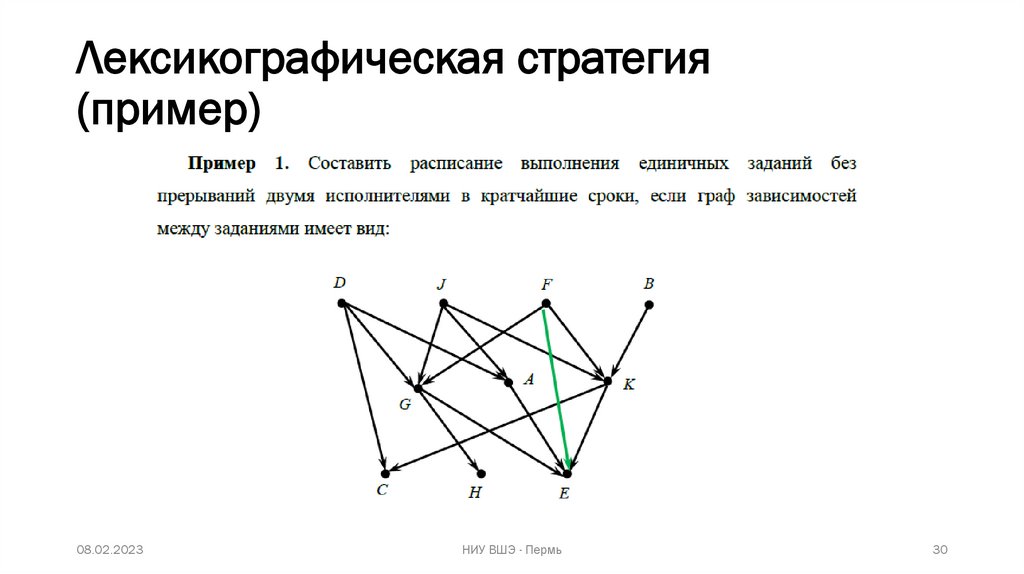
Бонусная задача: реализовать алгоритм лексикографической
стратегии для составления кратчайшего расписания выполнения
задач (отличается от уровневой стратегии тем, что прямых потомков у
задачи может быть несколько, и приоритеты выбираются исходя из
строкового представления всех приоритетов потомков в алфавитном
порядке (приоритеты потомков выставляются в строке по убыванию),
для назначения последующих приоритетов выбирается наименьшая
из строк приоритетов).
08.02.2023
НИУ ВШЭ - Пермь
29

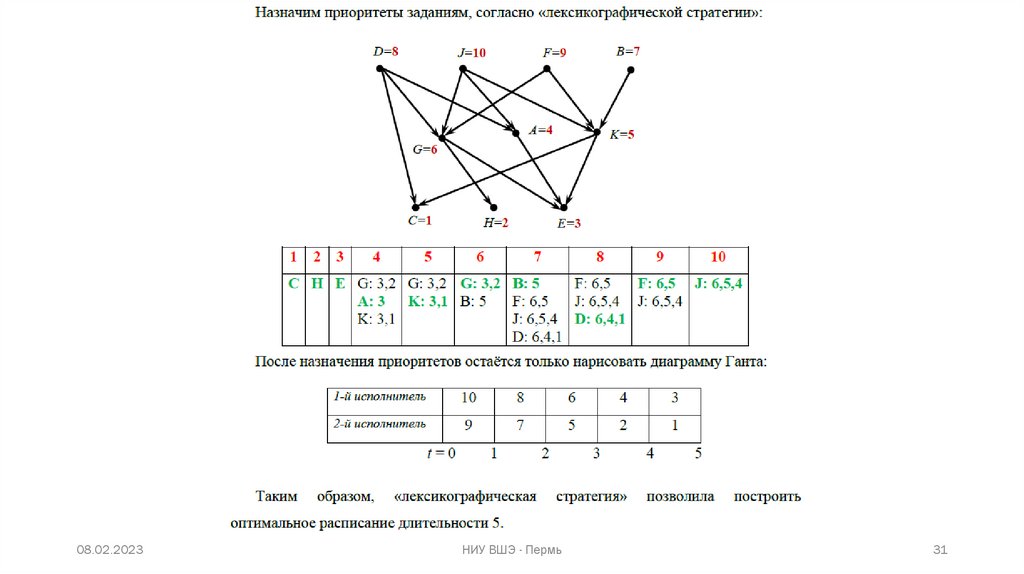
29.

Лексикографическая стратегия
(пример)
08.02.2023
НИУ ВШЭ - Пермь
30

30.

08.02.2023
НИУ ВШЭ - Пермь
31

31.

Практика №3 (3 модуль)
Паросочетания максимальное и
совершенное

32.

Паросочетания в графах
Паросочетание – набор рёбер, в котором никакие два ребра не
смежны. => Всякая вершина графа инцидентна не более чем одному
ребру, принадлежащему паросочетанию.
Вершины, покрытые паросочетанием – вершины, инцидентные рёбрам
из паросочетания.
Максимальное паросочетание – паросочетание в графе, содержащее
максимальное количество рёбер, среди всех паросочетаний в графе.
Чередующаяся цепь относительно паросочетания M – набор рёбер, при
котором оба конца цепи НЕ покрыты рёбрами из паросочетания M, а
каждая внутренняя (не концевая) вершина покрыта только одним ребром
из паросочетания M. Состоит только из нечётного числа рёбер. При
движении от одной концевой вершины к другой чередуются рёбра
принадлежащие и не принадлежащие паросочетанию M.
08.02.2023
НИУ ВШЭ - Пермь
33

33.

Паросочетания в графах
Теорема Бержа: Паросочетание M в двудольном графе является
максимальным тогда и только тогда, когда в графе нет удлиняющих цепей
(чередующихся относительно паросочетания M) => алгоритм, использующий
чередующиеся цепи.
Совершенное паросочетание – паросочетание, которое покрывает все
вершины графа.
Совершенное паросочетание всегда является максимальным, но
максимальное паросочетание не всегда является совершенным.
Теорема Холла: Для существования совершенного паросочетания в
двудольном графе необходимо и достаточно, чтобы в нём для каждого
подмножества S1 вершин из первой доли графа и множества S2 вершин из
второй, смежных вершинам подмножества S1, выполнялось неравенство:
=> алгоритм, использующий чередующиеся деревья.
08.02.2023
НИУ ВШЭ - Пермь
34

34.

Паросочетания в графах
^
Нет совершенного паросочетания
Паросочетание M: [v2, v5], [v4, v6]
< Совершенные паросочетания:
Чередующаяся цепь относительно M:
[A, E], [B, F], [C, D]
[v1, v5], [v5, v2], [v2, v6], [v6, v4], [v4, v3]
[A, 4], [B, 3], [C, 2], [D, 1], [E, 5]
Макс. паросочетание: [v1, v5], [v2, v3], [v4, v6]
08.02.2023
НИУ ВШЭ - Пермь
35

35.

Постановка задачи
Основная задача: придумать двудольные графы вручную по условиям.
Подобрать тесты (минимально по одному на каждое условие) и доказать их
правильность для паросочетаний в двудольном графе по пять вершин в
каждой доле. Использовать следующие условия:
1. В графе максимальное паросочетание является совершенным.
2. В графе есть максимальное паросочетание и не существует
совершенного.
По одному тесту без доказательства –> 0,3 балла, с доказательством –> 0,5 баллов
По два теста без доказательства –> 0,5 баллов, с доказательством –> 0,7 баллов
По три теста без доказательства –> 0,7 балла, с доказательством –> 0,9 баллов
+ 0,1 балл за идею прикладного использования максимального или совершенного паросочетания.
Бонусная задача: программно реализовать алгоритм нахождения
максимального или совершенного паросочетания.
08.02.2023
НИУ ВШЭ - Пермь
36

36.

Спасибо за внимание!