Similar presentations:
Рекурсия
1.
2.
Рекурсия3.
Понятие рекурсииРекурсивным называется объект, который
частично определяется через самого себя.
4.
5.
У попа была собака, он её любилОна съела кусок мяса, он её убил
В землю закопал,
Надпись написал:
«У попа была собака, он её любил
Она съела кусок мяса, он её убил
В землю закопал,
Надпись написал:
6.
Дом, который построил ДжекВот дом,
Который построил Джек.
А это пшеница,
Которая в темном чулане хранится
В доме,
Который построил Джек
А это веселая птица-синица,
Которая часто ворует пшеницу,
Которая в темном чулане хранится.
7.
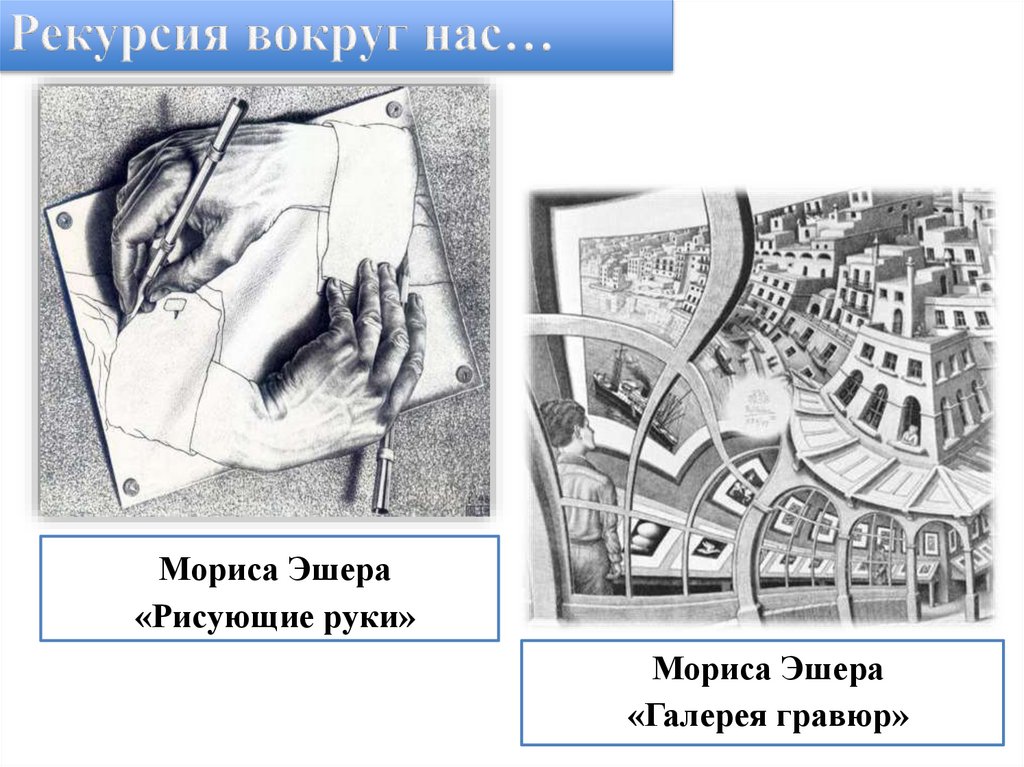
Мориса Эшера«Рисующие руки»
Мориса Эшера
«Галерея гравюр»
8.
Фрактал "Треугольник Серпинского"Эйфелева Башня в Париже
Исторический музей в Москве
9.
Дерево состоит из веток. Ветка в своюочередь состоит из более маленьких веточек.
Каждая ветка повторяет дерево.
Реки образуются из впадающих в них рек.
Чешуя шишек и семена некоторых цветов
(например, подсолнечника) расположены
пересекающимися спиралевидными веерами,
определяемыми
соотношением
чисел
Фибоначчи.
10.
Эффект Дросте - термин дляизображения специфического
вида
рекурсивного
изображения.
Изображение
включает
уменьшенный
собственный вариант самого
себя. Этот более малый
вариант
после
этого
показывает даже более малый
вариант себя, и так далее.
Практически это продолжается
пока разрешение изображения
позволяет уменьшает размер.
Термин был введен в честь
Дросте, голландского какао.
11.
Герб Российской Федерацииявляется
рекурсивноопределённым графическим
объектом: в правой лапе
изображённого
на
нём
двуглавого
орла
зажат
скипетр, который венчается
уменьшенной копией герба.
Так как на этом гербе в правой
лапе орла также находится
скипетр,
получается
бесконечная рекурсия.
12.
13.
Факториал числаРекурсивное определение:
5! = 5 * 4!
4! = 4 * 3!
3! = 3 * 2!
2! = 2 * 1!
1! = 1 * 0!
0! = 1
Нерекурсивное определение:
5! = 1 * 2 * 3 * 4 * 5 = 120
N! = 1 * 2 * ... * N, при N > 0
N! = 1 при N = 0
14.
Числа Фибоначчи• Нерекурсивное определение:
F1 = 1
F2 = 1
F3 = 1 + 1 = 2
F4 = 1 + 2 = 3
F5 = 2 + 3 = 5
F6 = 3 + 5 = 8
• Рекурсивное определение:
F6 = F5 + F4
F5 = F4 + F3
F4 = F3 + F2
F3 = F2 + F1
F2 = 1
F1 =1
15.
Плюсы рекурсивных алгоритмовСодержание и мощность рекурсивного
определения, а также его главное
назначение, состоит в том, что оно
позволяет
с
помощью
конечного
выражения
определить
бесконечное
множество объектов.
Использование рекурсии позволяет легко
(почти дословно) запрограммировать
вычисления по рекуррентным формулам.
16.
Программы, в которых используются
рекурсивные
алгоритмы
отличаются
простотой, наглядностью и компактностью
текста.
Рекурсивная процедура указывает, что
нужно делать, а нерекурсивная больше
акцентирует внимание на том, как нужно
делать.
17.
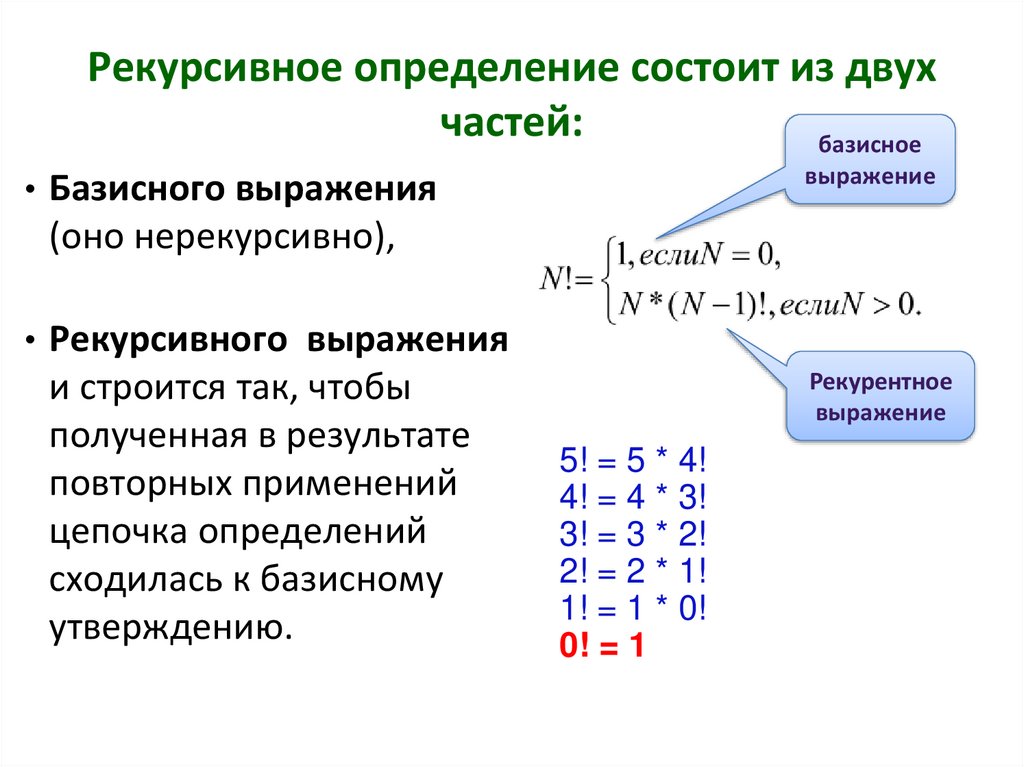
Рекурсивное определение состоит из двухчастей:
базисное
выражение
• Базисного выражения
(оно нерекурсивно),
• Рекурсивного выражения
и строится так, чтобы
полученная в результате
повторных применений
цепочка определений
сходилась к базисному
утверждению.
Рекурентное
выражение
5! = 5 * 4!
4! = 4 * 3!
3! = 3 * 2!
2! = 2 * 1!
1! = 1 * 0!
0! = 1
18.
Впрограммировании
подпрограмма, которая
вызывает сама себя.
алг Нерекурсивная функция
нач
. вывод "Введите число:"
. цел х
. ввод х
. вывод х,"! = ", факториал(х)
кон
алг цел факториал( цел х)
нач
. цел а, в
. а := 1
. в := 2
. нц пока в <= х
. . а := а * в
. . в := в + 1
. кц
. знач := а
кон
рекурсивной
в процессе
называется
выполнения
алг Рекурсия
нач
. вывод "Введите число:"
. цел х
. ввод х
. вывод х, " != ", Факториал(х)
кон
алг цел Факториал( цел а)
нач
. если а = 1 то
. . . знач := 1
. . иначе
. . . знач := а * Факториал(а-1)
. все
кон
19.
Выход из рекурсииЧтобы рекурсия не зацикливалась, необходимо соблюдать
два условия:
1) обязательно должно быть условие окончания рекурсии
(базисное выражение);
2) если есть параметр рекурсии, то он должен изменяться
таким образом , чтобы привести к условию окончания
рекурсии (базису)
алг цел Факториал( цел а)
нач
. если а = 1 то
. . . знач := 1
. . иначе
. . . знач :=а * Факториал(а - 1)
. все
кон
20.
Недостатки рекурсииОднако за простоту рекурсивных алгоритмов
приходится расплачиваться неэкономным
использованием оперативной памяти, так как
выполнение рекурсивных процедур требует
значительно большего размера памяти во время
выполнения.
При каждом рекурсивном вызове для локальных
переменных, а также для параметров процедуры,
выделяются новые ячейки памяти.


















 informatics
informatics








