Механик грунтов. Практические занятия

1. Механик грунтов практические занятия

Федеральное государственное бюджетное образовательное
учреждение высшего образования
Уфимский государственный нефтяной технический университет
Механик грунтов
практические занятия
Итоговый контроль – выполнение расчетнографической работы.

2. Механика грунтов

Для выполнения практических работ необходимо
прослушать лекции, изучить учебные пособия:
• Механика грунтов, основания и фундаменты: Учеб.
пособие для строит.спец.вузов/ С.Б. Ухов, В.В.
Семенов, В.В. Знаменский и др.; Под ред. С.Б. Ухов 5-е изд., -М.: Высш. шк., 2010.- 566 с.
• Добров, Э.М. Механика грунтов: учебник для студ.
высш.учебн. заведений./Э.М.Добров.- М.:
Издательский центр «Академия», 2008.-272 с.
• Абуханов, А.З. Механика грунтов: Учебное пособие/
Абуханов А.З.–Ростов н/Д: Феникс, 2006.-352 с.(Строительство).

3. Механика грунтов

На практических занятиях будем решать
задачи из сборника задач:
Механика грунтов [Электронный
ресурс] : сборник задач / УГНТУ, каф.
АДиТСП ; сост.: О. В. Галимнурова [и
др.]. - Уфа : УГНТУ, 2020. - 324 Кб. - Б. ц.
Задачи решаются по своему варианту

4.

Задачи на физические Ф.1-Ф.6,
прочностные
П.1
и
деформационные характеристики
Д.1
решаются
согласно
нормативных
документов,
лекций, учебной литературой.

5. Б.1

• Определить и построить эпюру напряжений от
собственного веса грунта с напластованием,
представленном в таблице.
Внимание. Вам предоставляют варианты определения
напряжения в от собственного веса. Посмотрите
внимательно и примените к своей задаче. У вас по
условию напластование состоит из трех слоев. Вам
нужно построить эпюру бытовых давлений, справа
написать
значения
напряжений,
слева
все
характеристики грунта. На схеме показать мощность.
На схеме должны быть только цифровые
значения.

6.

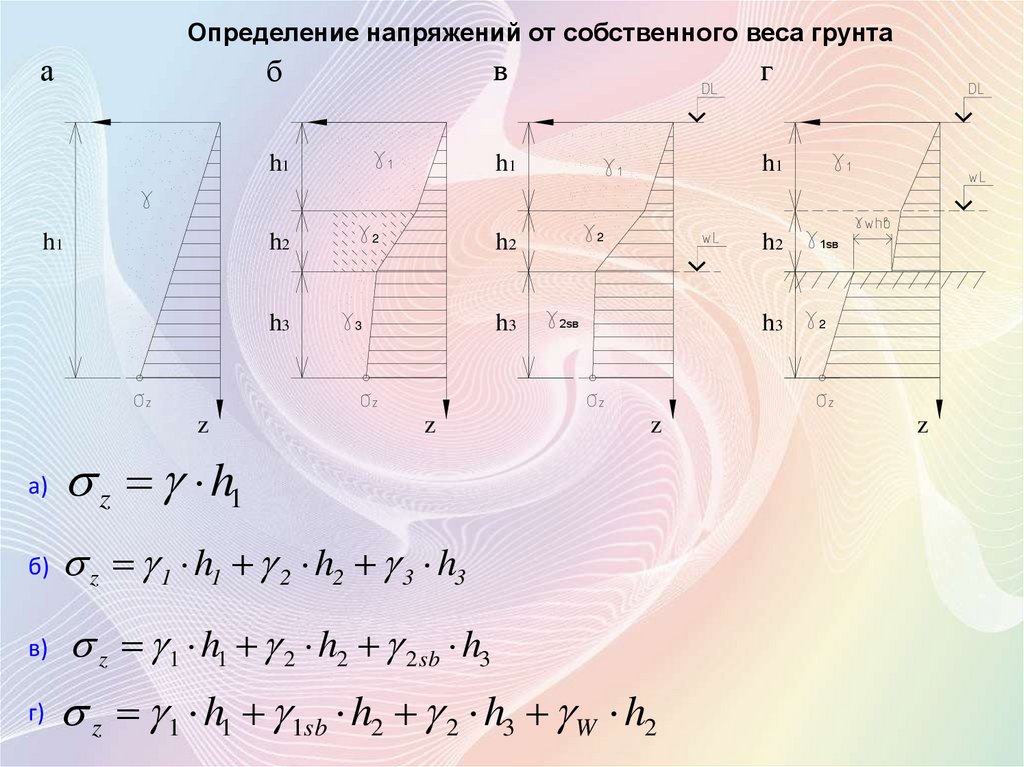
Определение напряжений от собственного веса грунта
а
h1
б
в
г
h1
h1
h1
h2
h3
z
а)
h2
2
h3
3
z
2
2sв
z
z h1
б) z 1 h1 2 h2 3 h3
в)
z 1 h1 2 h2 2 sb h3
г)
z 1 h1 1sb h2 2 h3 W h2
h2
1sв
h3
2
z

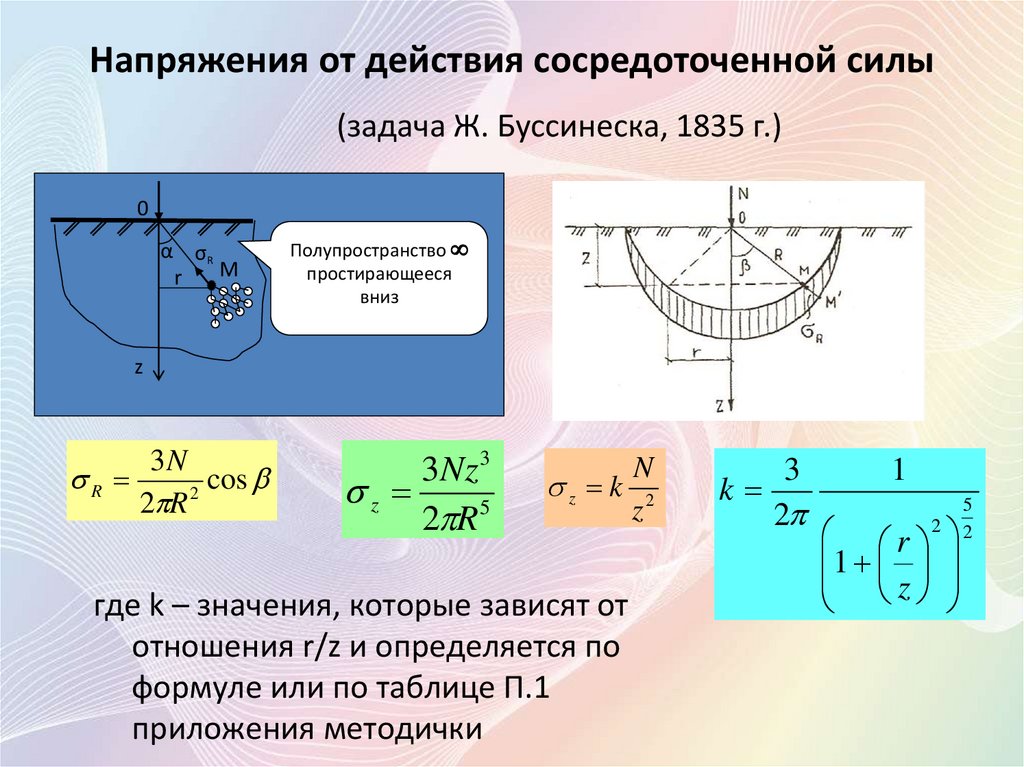
7. Напряжения от действия сосредоточенной силы (задача Ж. Буссинеска, 1835 г.)

0
α σR
М
r
Полупространство
простирающееся
вниз
z
3N
R
cos
2
2 R
3Nz 3
z
2 R5
N
z k 2
z
где k – значения, которые зависят от
отношения r/z и определяется по
формуле или по таблице П.1
приложения методички
k
3
2
1
r 2
1
z
5
2

8. Н.1

• Построить
эпюру
вертикальных
сжимающих напряжений от вертикальной
сосредоточенной нагрузки Р по оси z, с
шагом 1 м на глубину 8 м. Сила Р
приложена на расстояние r от оси z.
Решение задачи выполнять в таблице (см.
таблицу 1, с.6).
Дано: Р, r.

9. Напряжения от действия группы сил

n
N3
N1
N2
Ni
z k1 2 k 2 2 k 3 2 k i 2
z
z
z
z
i 1
1 n
z 2 ki N i
z i 1
где k – значения, которые зависят от отношения r/z и
определяется по формуле или по таблице П.1 приложения
методички

10. Н.2

• К горизонтальной поверхности массива грунта приложено
несколько сосредоточенных сил: Р1 , Р2 , Р3 на расстояниях r1,
r2.Определить величины вертикальных напряжений σz от
совместного действия сосредоточенных сил в точках массива
грунта по вертикали I-I, проходящей через точку приложения
силы Р2.
• Точки по вертикали располагаются на расстоянии от дневной
поверхности: точка 1 – 2,0 м; точка 2 – 4,0 м; точка 3 – на расстоянии
6,0 м; точка 4 – 8,0 м; точка 5 – 12,0 м
• По вычисленным напряжениям и заданной оси I-I построить эпюру
распределения напряжений σz. Схема к расчету представлена на
рис. Решение выполнять в табличной форме (см. таблицу 2, с.6).
• Дано: Рi, ri.

11. Н.3

• К горизонтальной поверхности массива грунта приложено
несколько сосредоточенных сил: Р1 , Р2 , Р3 на расстояниях
r1, r2. Определить величины вертикальных напряжений σz
от совместного действия сосредоточенных сил в точках
массива грунта по горизонтали II-II, проходящей на
глубине σz от поверхности массива грунта. Точки по
горизонтали расположить вправо и влево от оси действия
силы Р2 на расстоянии 0; 1,0; 4,0 м.
По вычисленным напряжениям и заданной оси II-II
построить эпюру распределения напряжений σz. Схема к
расчету представлена на рис. Решение выполнять в
табличной форме (см. таблицу 2, с.6).
• Дано: Рi, ri, z.

12. Напряжения от полосовой нагрузки

z р
где α - коэффициент рассеивания напряжений,
определяемый по СНиП 2.02.01-83* в зависимости от
формы фундамента (круглая, квадратная или
прямоугольная или полосовая), принимаем по
таблице П.2 в зависимости от ξ =2z/b (где b-ширина
полосы, z глубина, м. и от η≥ 10.
p - равномерное распределенное давление.

13. Н.5

• На основание действует равномерно
распределенная нагрузка р, приложенная
полосой шириной b (см.рис.). Определить
вертикальное сжимающее напряжение σz на
глубине z в точке М ив точках по оси ОZ.
Построить
эпюру
напряжений
(для
построения эпюры определить напряжения
не менее чем 7…8 точек), определяя
напряжения с шагом 0,2b. Решение
выполнять в табличной форме (см.
таблицу 3, с.6).
• Дано: р, z, а.

14. Определение напряжений методом угловых точек

Сущность метода: грузовая площадь разбивается на такие
прямоугольники, в которых рассматриваемая точка оказалась бы
угловой. Напряжение в этой точке определяется как сумма
напряжений от прямоугольных площадок, для которых эта точка
является угловой.
ВАРИАНТ нагружения:
Точка С вне прямоугольника загрузки (рис. ).
В этом случае ее считают угловой для
четырех фиктивных площадей загружения:
cfmk (I), cdef (ll), cbnk (III) и сдаb (IV).
Тогда
σz = σzI+ σzII - σzIII - σzIV =0.25(αI +αII-αIII-αIV)p
где α - коэффициент рассеивания напряжений,
определяемый по СНиП 2.02.01-83*(приложение
таб. П.2) в зависимости от формы площадки
загружения
(круглая,
квадратная
или
прямоугольная),
соотношения
сторон
прямоугольного фундамента η = l/b и
ξ = z/b,
p - равномерное распределенное давление.

15. Т.1

По методу угловых точек найти величину
сжимающих
напряжений
в
точке
О,
расположенной на глубине z вне контура
равномерно
загруженного
участка
ABCD
размером l×b.
• Схема расположения точки показана на рисунке.
Решение выполнять в табличной форме(см.
таблицу 4, с.6).
• Дано: р, l, b, z, х, y.

16. Определение напряжений методом угловых точек

Сущность метода: грузовая площадь разбивается на такие
прямоугольники, в которых рассматриваемая точка оказалась бы
угловой. Напряжение в этой точке определяется как сумма
напряжений от прямоугольных площадок, для которых эта точка
является угловой.
ВАРИАНТ нагружения:
Загруженная площадь разбивается на два прямоугольника
авдс (I), cdfe (II), для каждого из которых точка С является
угловой. Тогда напряжение в точке С определяется как
сумма двух угловых напряжений в прямоугольниках I и II
(рис. а):
σz= σzI+ σzII=0.25(αI +αII)p
где α - коэффициент рассеивания напряжений,
определяемый по СНиП 2.02.01-83*(приложение
таб. П.2) в зависимости от формы площадки
загружения
(круглая,
квадратная
или
прямоугольная),
соотношения
сторон
прямоугольного фундамента η = l/b и
ξ = z/b,
p - равномерное распределенное давление.

17. Т.2

Методом угловых точек определить сжимающие
напряжения на глубине z в точке О, находящейся,
от
контура
равномерно
загруженного
прямоугольного фундамента размером l×b, на
расстоянии а напротив середины длиной стороны.
Решение выполнять в табличной форме(см.
таблицу 4, с.6).
Дано: р, l, b, z, а.

18. Определение напряжений методом угловых точек

Сущность метода: грузовая площадь разбивается на такие
прямоугольники, в которых рассматриваемая точка оказалась бы
угловой. Напряжение в этой точке определяется как сумма
напряжений от прямоугольных площадок, для которых эта точка
является угловой.
ВАРИАНТ нагружения:
Точка С внутри прямоугольника давлений (рис. б),
тогда загруженная площадь разбивается на
четыре прямоугольника: свад (I), свкп (II), cdef
(III), cnmf (TV):
σz= σzI+ σzII+ σzIII + σzIV =0.25(αI +αII+αIII+αIV)p
где α - коэффициент рассеивания напряжений,
определяемый по СНиП 2.02.01-83*(приложение
таб. П.2) в зависимости от формы площадки
загружения
(круглая,
квадратная
или
прямоугольная),
соотношения
сторон
прямоугольного фундамента η = l/b и
ξ = z/b,
p - равномерное распределенное давление.

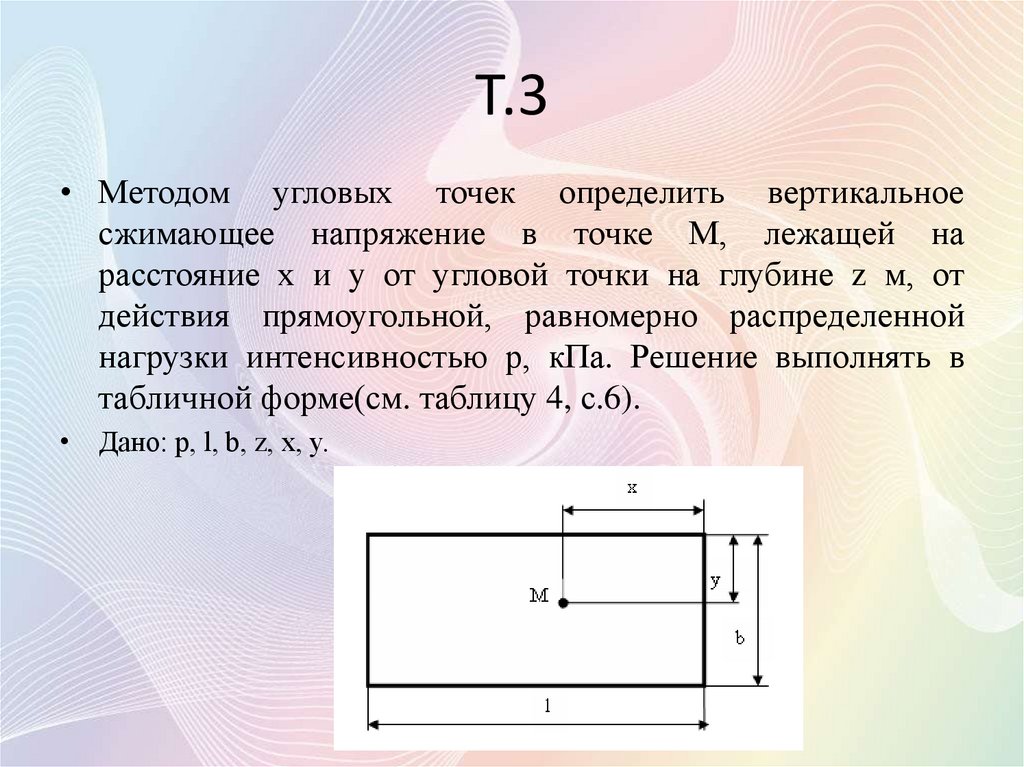
19. Т.3

• Методом угловых точек определить вертикальное
сжимающее напряжение в точке М, лежащей на
расстояние х и y от угловой точки на глубине z м, от
действия прямоугольной, равномерно распределенной
нагрузки интенсивностью р, кПа. Решение выполнять в
табличной форме(см. таблицу 4, с.6).
• Дано: р, l, b, z, x, y.