Математическое моделирование

1.

Джордж Пойа

2.

Тема урока
Математическое
моделирование

3.

Математическая модель
Числовые и буквенные выражения.
Формулы.
Уравнения.
Неравенства.
Функции и графики.
Математическое моделированиеобласть математики, которая
занимается построением и
изучением математических моделей

4.

Прикладные задачи
Классификация текстовых задач
Задачи на движение.
Задачи на смеси и сплавы.
Задачи на проценты.
Задачи на работу.

5.

Этапы решения прикладных задач:
1. Построение математической модели.
2. Решение математической задачи.
3. Анализ полученного результата, исходя
из содержания прикладной задачи.

6.

Что это?
(из лат. tabula
? ? ?— доска)- способ структурирования
Таблица
данных. Представляет собой распределение
данных по однотипным строкам и
столбцам.

7.

Математическая модель, с помощью
которой можно удобно и наглядно
представить информацию данную в
условии задачи.
Таблицы

8.

Цель урока:
научиться использовать таблицы для
решения задач алгебраическим
способом.

9.

Основные принципы работы с таблицей
1. Таблица должна быть «живой», действенной
моделью, создаваться самим человеком.
2. Таблица должна помогать анализу данных, не
обременять решение.

10.

Использование таблиц для решения текстовых задач
по математике

11.

12.

Что необходимо делать? (при решении задач на работу)
Задачу прочти
Немного помолчи
Про себя повтори
Ещё раз прочти
Нет объёма работы, за 1 прими
Объём выполненной работы выражают как
часть этой единицы!
Данные в таблицу занеси
Уравнение запиши
Уравнение реши
При совместной работе производительности
складываются и приравниваются к общей!

13.

Задачи
(Заполните таблицы и составьте уравнения)
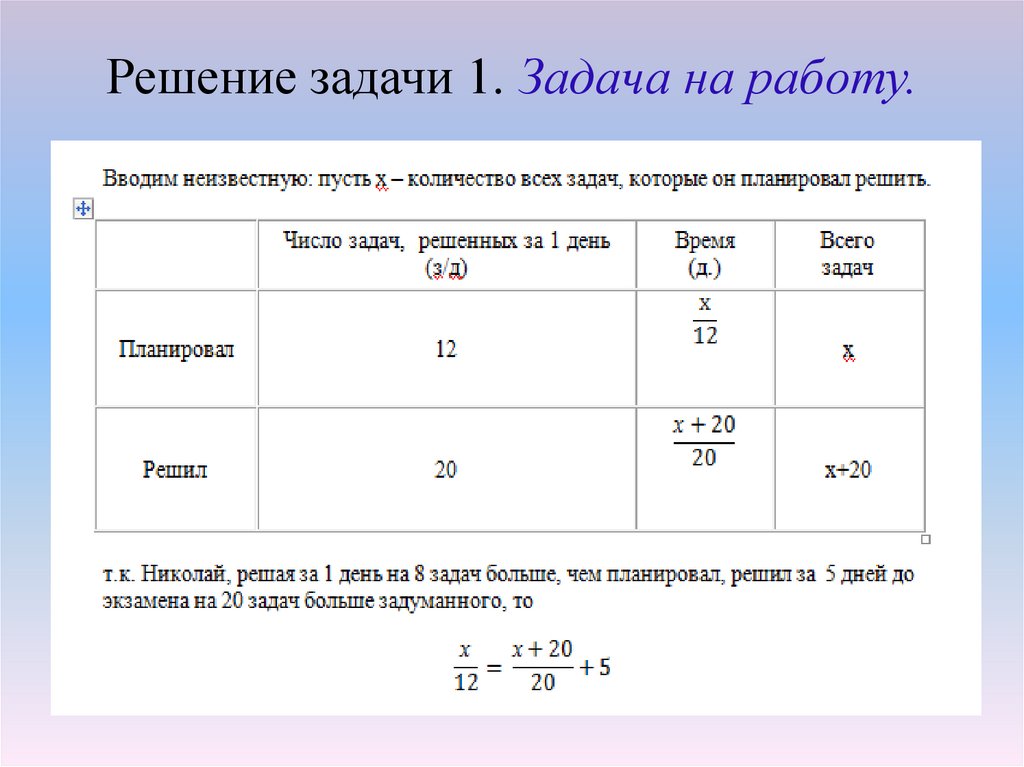
Задача 1. Задача на работу.
Николай рассчитал, что он сможет хорошо приготовиться к экзамену, если
будет до экзамена решать по 12 задач в день. Однако ежедневно он
перевыполнял свою норму на 8 задач и уже за 5 дней до экзамена решил на
20 задач больше, чем планировал первоначально. Сколько задач решил
Николай?
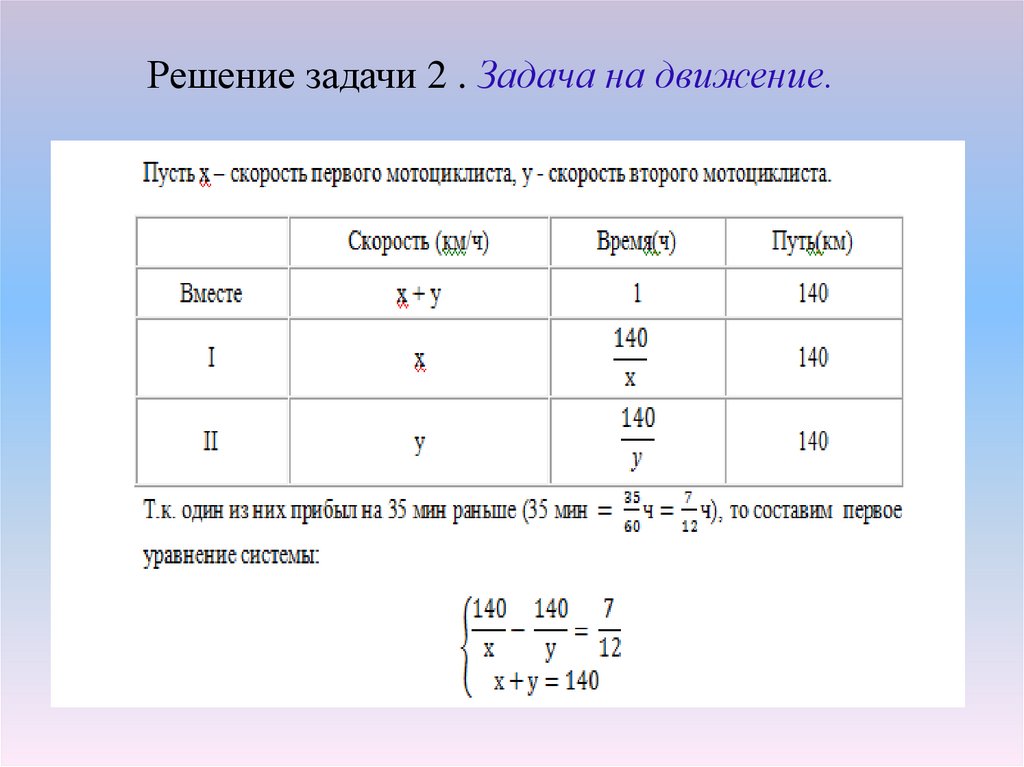
Задача 2. Задача на движение.
Два мотоциклиста выехали одновременно из городов А и В навстречу друг
другу. Через час они встретились и, не останавливаясь, продолжили
двигаться. Один из них прибыл в город А на 35 мин раньше, чем второй – в
город В. Найдите скорость каждого мотоциклиста, если расстояние между
городами составляет 140 км.

14.

Решение задачи 1. Задача на работу.

15.

Решение задачи 2 . Задача на движение.

16.

Рефлексия
1. Перечислите типы задач, которые мы
рассмотрели на уроке.
2. Назовите этапы решения задач.
3. Какие математические модели
используют при решении задач?
4. Какова была цель урока?
5. Сколько задач из 6 предложенных,
удалось решить самостоятельно?

17.

Домашнее задание
1) N из учебника 486, 488.
2) Подготовить решения 2 задач из тестов
ОГЭ по данной теме.

18.

19.

Всем
спасибо !