Similar presentations:
Skaitļu formāti. Peldošais punkts
1.
Ievads datoru arhitektūrāDST203
3. lekcija
Skaitļu formāti. Peldošais punkts
Asoc.prof., Dr.sc.ing, Dmitrijs Bļizņuks
1
2.
SatursPeldošais punkts binārā sistēmā
IEEE 754 standarts
IEEE 754 speciālie gadījumi un kļūdas
2
3.
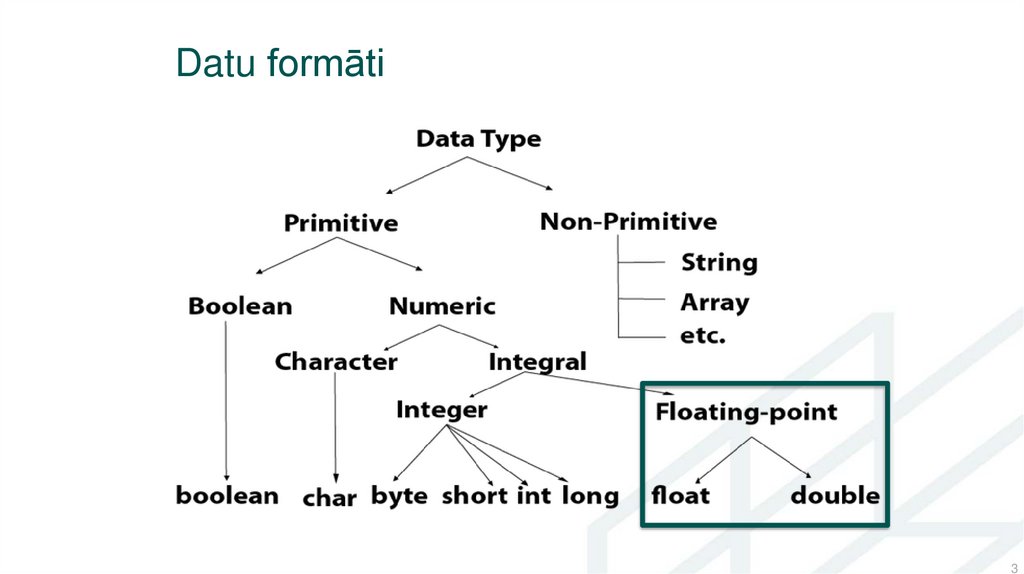
Datu formāti3
3
4.
Kā norādīt punktu izmantojot tikai 0 un 1?Noteikt fiksēto ciparu (bitu) pirms un pēc komata?
– XX.YY? 65535.65535-1 65535,0000152
– Nav efektīvi, jo ierobežo gan maksimālo vērtību, gan precizitāti.
Izveidot divus atsevišķos tipus priekš lieliem skaitļiem un maziem?
– A) X.YYY -> 255.16777216-1 -> 255.0000000596
– B) XXX.Y
– Nav ērti, neatrisina problēmu
Definēt punkta atrāšanas pozīciju ar atsevišķo kodu līdzīgi kā String formātam?
– Zaudējam vienu baitu
4
4
5.
Peldoša punkta (komata) formātiC# tips
Aptuvēns diapazons
−45
float
±1,5 x 10
double
±5,0 × 10
decimal
±1,0 x 10
to
Precizitāte
±3,4 x 10
−324
to ±1,7 × 10
-28
to ±7,98 x 10
38
308
28
Izmērs
~6-9 cipari
4 baiti
~15-17 cipari
8 baiti
28-29 cipari
16 baiti
5
5
6.
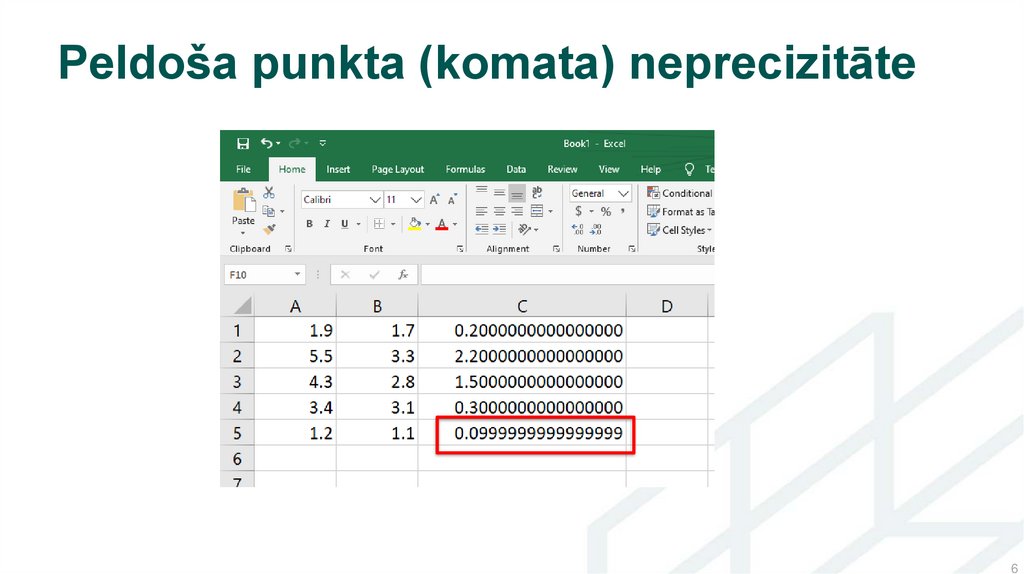
Peldoša punkta (komata) neprecizitāte6
6
7.
Peldošais punkts binārā formātāPieņemsim ka mums jāpārveido 252,390625 binārajā kodā
Pārveidojam 252 binārajā formā, 252 = 11111100
Nākamā darbība ir pārveidot 0,390625 binārajā formā. Lai to veiktu
mēs reizināsim ar 2 un rezultātā pierakstīsim to kas ir kreisajā
pozīcijā
0,390625 * 2 = 0,78125
0,78125 * 2 = 1,5625
0,5625 * 2 = 1,125
0,125 * 2 = 0,25
0,25 * 2 = 0,5
0,5 * 2 = 1,0
0
0
1
1
0
0
1
Atbilde: 11111100,011001
7
7
8.
PiemērsKā attēlojas 3,625 binārajā formā?
011,101
Kā attēlojas 0,1 binārajā formā?
0,1 * 2 = 0,2
0,2 * 2 = 0,4
0,4 * 2 = 0,8
0,8 * 2 = 1,6
0,6 * 2 = 1,2
0,2 * 2 = 0,4
… bezgalīgi
Līdzīgs princips ir citos skaitļošanas sistēmās. Jāreizina ar skaitļošanas sistēmas bāzi.
8
8
9.
Binārais uz decimāloBinārais uz decimālo: 1100,0110012 = ?10
Pārveidot 11002 viegli:
11002 = 0 * 20 + 0 * 21 + 1*22 + 1*23 = 4+8 = 1210
Daļskaitli ,011001 nepieciešams reizināt un summēt,
bet jāsāk ar 2-1
,011001 = 0*2-1+1*2-2+1*2-3+0*2-4+0*2-5+1*2-6
Saskaitot kopā:
= 1 / 4 + 1 / 8 + 1 / 64
= 0,25 + 0,125 + 0,015625
= 0,390625
Galā rezultāts 12,39062510
9
9
10.
PiemērsPārveidot no binārā uz decimālo 100,11012 = ?10
Veselā daļa — 1002 = 4 10
Daļskaitlis — ,11012 = 1/2 +1/4 +1/16 = 0,5 + 0,25 + 0,0625 = 0,8125 10
Saskaitot kopā — 4,8125 10
10
10
11.
Zinātniskais pieraksts (normālforma)Paņemsim decimālo skaitļi 201,0910
To var arī pierakstīt kā 00201,090010
Jānoskaidro, kuri cipari ir zīmīgie:
– Jebkurš nē nulles cipars vienmēr ir zīmīgs,
– Nulle nav zīmīgā ja atrodas pa kreisi no veselas daļas un pa labi no
daļskaitļa.
Jāpārnes komatu tā, lai pirms komata (veselā daļā) būtu
viens zīmīgs cipars un jāsareizina ar 10n, lai rezultāts
nemainītos.
2,010900 * 102
Daļskaitlī ir līdzīgi, bet jāreizina ar 10-n
0,00020109 = 2,0109 * 10-4
987600*100 = 98760*101 = 9876*102
11
11
12.
IEEE 754 formātsLai attēlot skaitļi IEEE 754 formāta, jāpārveido
binārā zinātniskā pierakstā
Piemēram:
• 0,1562510 = 0,001012
• 1,01 * 2-3
Sastāvdaļas: (Zīme) * (Mantisa) * 2 (eksponenta)
Standartformā (‘single precision’) ir 32 biti:
12
12
13.
IEEE 754 formātsEksponenta satur 8 bitus, tātad var glabāt skaitļus 0 līdz 255
Kā saglabāt negatīvo eksponenti, lai attēlo skaitļus mazākus par 0?
Tāpēc eksponenta tiek nobīdīta par 127
Nobīdīta eksponenta = 127 + sākotnēja eksponenta
Nobīdīts Dec.
Binārais
0
127 +
0 = 127
01111111
1
127 +
1 = 128
10000000
2
127 +
2 = 129
10000001
128
127 + 128 = 255
11111111*
-1
127 –
01111110
Dec.
-127
1 = 126
127 – 127 =
0
00000000*
13
13
14.
IEEE 754 formātsPiemērs 1,001011* 23
Eksponenta – 3
Izmantojot nobīdi 127, tiek saglabāts 127+3 = 13010 vai 100000102
0 10000010 MMMMMMMMMMMMMMMMMMMMMMM
1
8
23
Mantisa
0 10000010 10010110000000000000000
1
8
23
14
14
15.
IEEE 754 formātsZinātniskā pierakstā nulle nekad nebūs kā pirmā zīmīgā
Tātad pirmais zīmīgais cipars vienmēr būs 1
Tāpēc nav nepieciešams vienmēr attēlot šo 1. To neattēlo un sauc
par “slēpto bitu” (’hidden bit’)
Tas ļauj iegūs papildus vienu precizitātes bitu
Rezultātā mantisa skaitlim 1,001011* 23
0 10000010 00101100000000000000000
1
8
23
15
15
16.
ApkopojotZīmes bits = 0
Eksponenta = 10000010
Mantisa = 00101100000000000000000
Vai: 0100 0001 0001 0110 0000 0000 0000 00002
Vai: 41 16 00 0016
16
16
17.
PiemērsPārveidojām –10,4375 IEEE 754 formātā
Atbilde
1 10000010 01001110000000000000000
1
8
23
17
17
18.
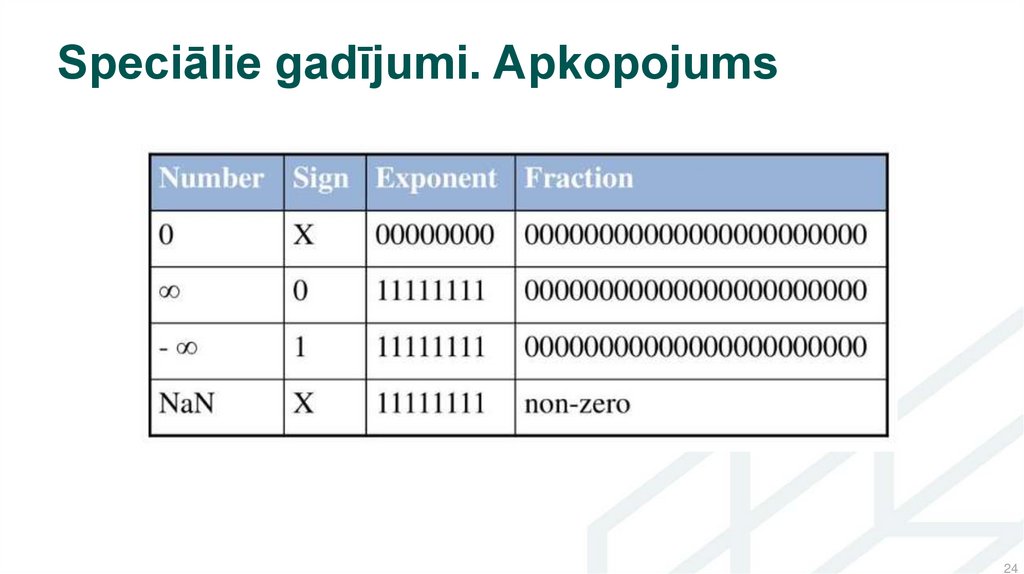
Speciālie gadījumiIr nepieciešams attēlot dažus speciālus gadījumus:
– +/- bezgalība,
– precīzi nulli,
– kļūdu.
Speciālos gadījumus attēlo, ierakstot eksponentē vienādus ciparus 0 vai 1
S
S
11111111
00000000
MMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMM
18
18
19.
Speciālie gadījumi. Denormālizētie skaitļiPirmais speciālais gadījums ir denormālizēts skaitlis, kas ļauj palielināt precizitāti
S
00000000
MMMMMMMMMMMMMMMMMMMMMMM
Kad eksponenta ir 2-127, tas vairs nav tipisks peldošā punkta skaitlis
Tas ļauj attēlot mazus skaitļus starp 0 un 1*2-126, to sauc par pakāpēnisko
izzudumu (‘gradual underflow’),
19
19
20.
Speciālie gadījumi. Denormālizētie skaitļiLai izskaidrot, apskatīsim netipisko formātu ar 8 bitiem, nevis 32
Eksponentē ir 4 biti un mantisā – 3
20
20
21.
Speciālie gadījumi. Precīzi nulleS
00000000
00000000000000000000000
Tikai tā var attēlot precīzi nulli
Sanāk 0 * 2-126, kas ir 0
21
21
22.
Speciālie gadījumi. BezgalībaAizpildot eksponenti ar 1 un mantisu ar 0, tiek attēlota bezgalība
Atkarībā no zīmes bita, tā var būt pozitīvā vai negatīvā
S
11111111 00000000000000000000000
Eksponentei būtu jābūt 255 – 127, kas rezultātā dod 128, bet šāda
eksponenta ir rezervētā bezgalībai,
Pozitīvā bezgalība: 0 11111111
00000000000000000000000
Negatīvā bezgalība: 1 11111111
00000000000000000000000
22
22
23.
Speciālie gadījumi. NaNTrešais speciālais gadījums ir kad eksponentes laukā ir visi 1 bet mantisa ir
atšķirīga no nulles vērtība. Šis gadījums tiek saukts par NaN (Not a Number);
Šajos gadījumos zīme netiek ņemta vērā;
NaN iegūst dalot 0 ar 0 vai citos nedefinētas aritmētikas gadījumos (tomēr dalot
kaut ko ar 0 iegūstam bezgalību);
Not a Number (NaN): X 11111111 XXXXXXXXXXXXXXXXXXXXXXX
23
23
24.
Speciālie gadījumi. Apkopojums24
24
25.
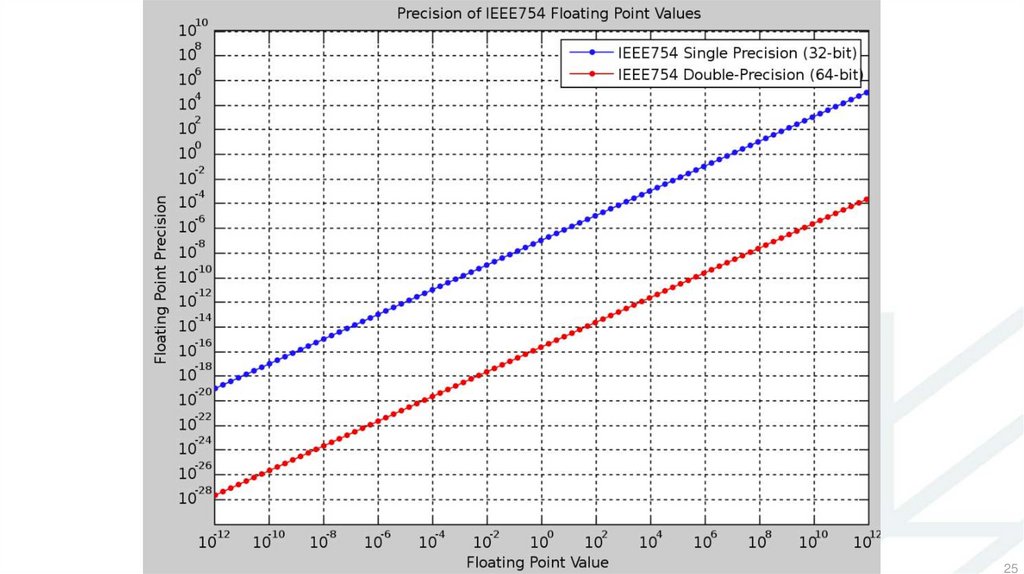
2525
26.
Peldoša punkta kļūdasJa mums ir vienāds bitu skaits, tad peldošais punkts būs neprecīzāks
nekā veselo skaitļu formātam ar tādu pašu bitu skaitu
Piemēram 8 bitu gadījumā ar nenobīdītu eksponenti un bez speciālajiem
gadījumiem (bet ar slēpto bitu):
EEE MMMMM
3
5
Gadījumā ja eksponente un mantisa satur tikai 0 tad tas ir 1,0 * 20 = 1
Gadījumā ja eksponente un mantisa satur tikai 1 tad tas ir 1.11111* 27
=11111100 jeb 252
–
Gadījumā ja eksponente un mantisa satur tikai 0, mazākais ko var
attēlot ir 1,000002 * 20 tātad 1,
–
Gadījumā ja eksponente un mantisa satur tikai 1, tad lielākais ko var
attēlot ir 1,11111 2 * 27 tātad 252,
Protams peldošais punkts var attēlot daļas ko savukārt nevar veselie
skaitļi
26
26
27.
Peldoša punkta kļūdasJa lielākais skaitlis ir 252, kāds būtu tuvākais?
Binārā formā 111 111102
Kas ir 1,11110 * 27 = 111110002 vai 248
Tiek zaudēti četri veselie skaitļi;
Nākošais tuvākais būtu: 111 111012
Kas ir 1,11101 * 27 = 111101002 vai 244
Un vēl četri veselie skaitļi
Lielākām vērtībām ir maksimāls zaudējums, jo to pastiprina
eksponente
27
27
28.
Peldoša punkta kļūdasDēļ noapaļošanas mantisas un eksponentes laukos ir iespējami gadījumi
kad peldoša punkta skaitļi nebūs identiski
Tas ir līdzīgi kā gadījumā ar 0.210 attēlošanu binārā kodā
Piemēram pieskaitot 0.2 kādam skaitlim 100,000 reizes rezultātā neiegūs
pieaugumu par 20 000
Šī iemesla dēļ lietojot peldoša punkta aritmētiku nākas pārbaudīt skaitļus
kādās robežās (piemēram, >=19999.99 un <= 20000.01)
28
28
29.
Peldoša punkta operācijas1.
Pirmā darbība ir pārbaudīt vai kāds no operandiem nav 0 (vai cits
speciāls gadījums). Ja ir tad rezultāts ir zināms uzreiz.
2.
Saskaitīšanas vai atņemšanas gadījumos jāsaskaņo mantisas, jo nevar
veikt darbību ja operandu eksponentes ir dažādas.
3.
Veikt darbības ar mantisām.
4.
Normalizēt rezultātu. Pārbaudot vai nav iegūts kāds izņēmums – izzūdi
(underflow) vai pārpildīšanās (overflow).
5.
Reizināt ir vieglāk jo vajag tik saskaitīt eksponentes un sareizināt
mantisas.
6.
Dalīšanas gadījumā vajag atņemt eksponentes un izdalīt mantisas.
29
29
30.
Papildus materiālihttp://en.wikipedia.org/wiki/Computer_number_format
http://en.wikipedia.org/wiki/Floating_point
http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
30
30


























 electronics
electronics





