Момент завинчивания гаек и винтов

1. РАЗДЕЛ 2. СОЕДИНЕНИЯ ДЕТАЛЕЙ

Лекция 4

2.

МОМЕНТ ЗАВИНЧИВАНИЯ ГАЕК И ВИНТОВ
Момент завинчивания гаек и винтов затрачивается
на преодоление момента трения на опорной
поверхности головки винта или гайки (Топорн ) и
преодоление сопротивления резьбы (Трезьбы ):
Tзав Fраб L Tрезьбы Tопорн
а) Момент сопротивления резьбы:
T резьбы Ft 2 резьбы d 2 2 Ft 2 раб d 2 2
где Ft2 резьбы – окружная сила сопротивления резьбы, на
среднем радиусе резьбы;
Ft2 раб
– окружное усилие рабочего, приведённое
к среднему радиусу резьбы.
Ft 2 раб
Fраб L
d2 2
Fраб 40
(1)

3.

FX
ТОПОРН 0
d2
L 40
2
Ft2 РЕЗЬБЫ
Ft2 РАБ
FРАБ
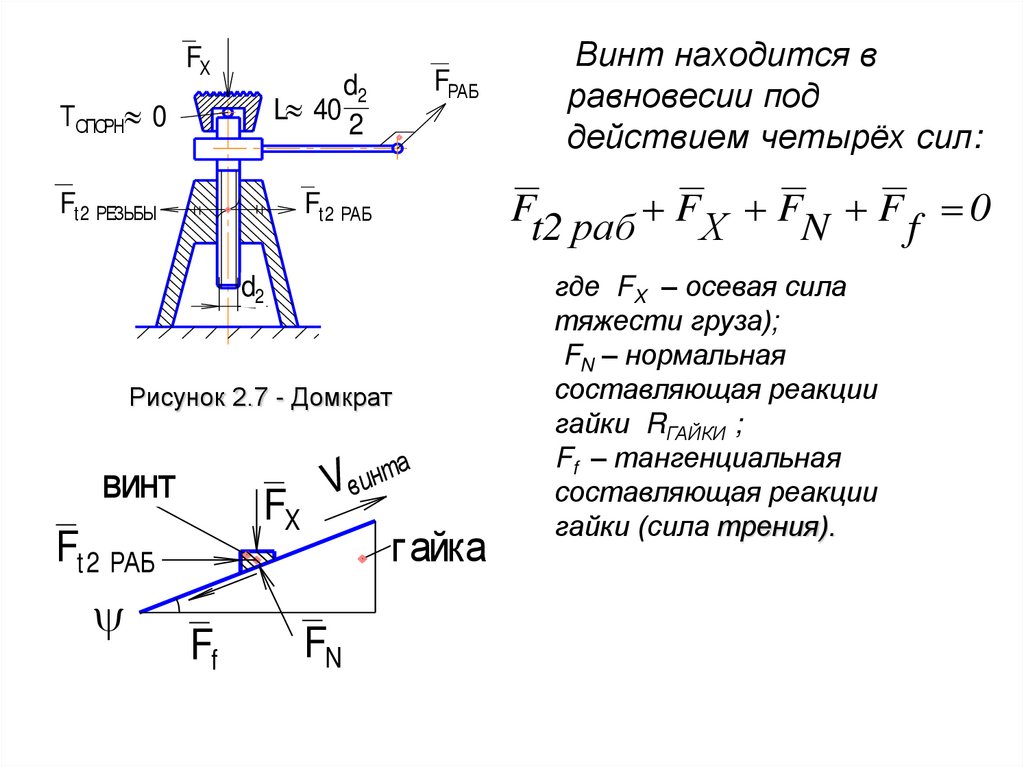
Ft2 раб FХ FN F f 0
d2
Рисунок 2.7 - Домкрат
винт
FX
Ft 2 РАБ
Ff
та
н
и
Vв
г айка
FN
Винт находится в
равновесии под
действием четырёх сил:
где FX – осевая сила
тяжести груза);
FN – нормальная
составляющая реакции
гайки RГАЙКИ ;
Ff – тангенциальная
составляющая реакции
гайки (сила трения).

4.

FN
ГАЙКИ
R
ГАЙКИ
Ft2 РАБ
Ff
R
FX
+
ВИНТА
FX + F
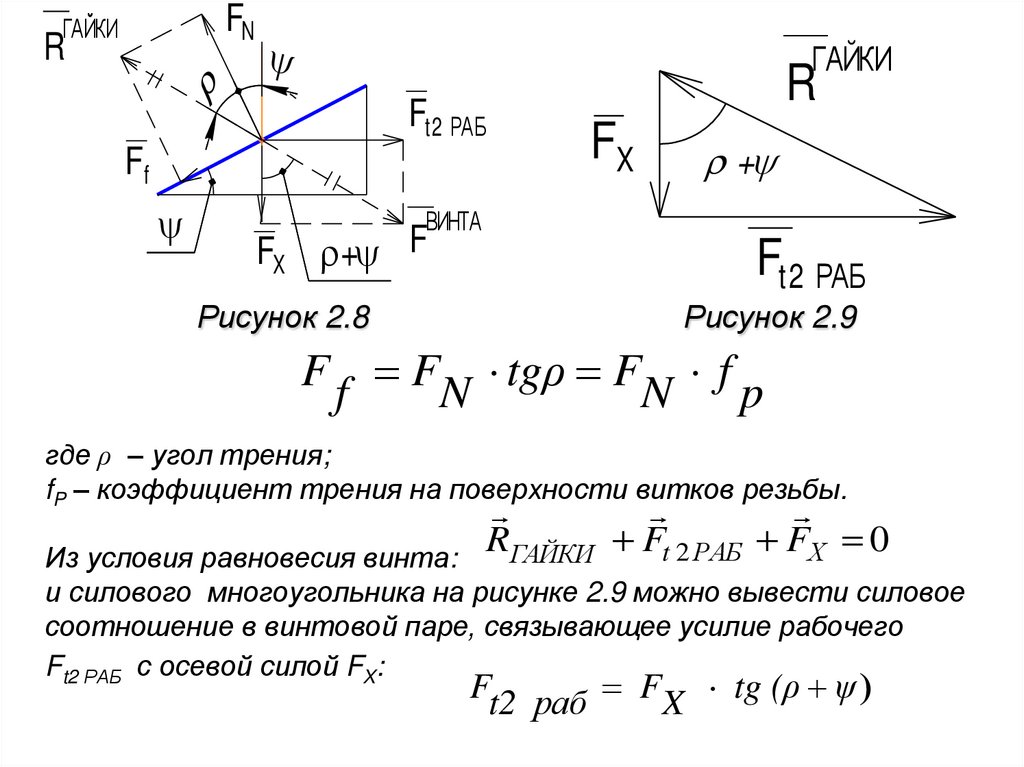
Рисунок 2.8
Ft2 РАБ
Рисунок 2.9
F f FN tgρ FN f p
где ρ – угол трения;
fP – коэффициент трения на поверхности витков резьбы.
RГАЙКИ Ft 2 РАБ FХ 0
Из условия равновесия винта:
и силового многоугольника на рисунке 2.9 можно вывести силовое
соотношение в винтовой паре, связывающее усилие рабочего
Ft2 РАБ с осевой силой FX:
Ft2 раб FX tg (ρ ψ

5.

При ρ+Ψ ≈ 11...130
tg(ρ+Ψ) ≈ 0,2...0,25.
Следовательно, винтовая пара, за счёт клинового
эффекта, даёт выигрыш в силе примерно в 4...5 раз.
Подставив последнее выражение в формулу (1) получим:
Т РЕЗЬБЫ Ft2 РАБ
d2
2
FХ tg (ρ ψ)
d2
2
б) Момент сопротивления опорной поверхности:
Т
F r F f r
опор
f f
X оп f

6.

где Ff – сила трения на опорной поверхности;
fОП – коэффициент трения на опорной поверхности.
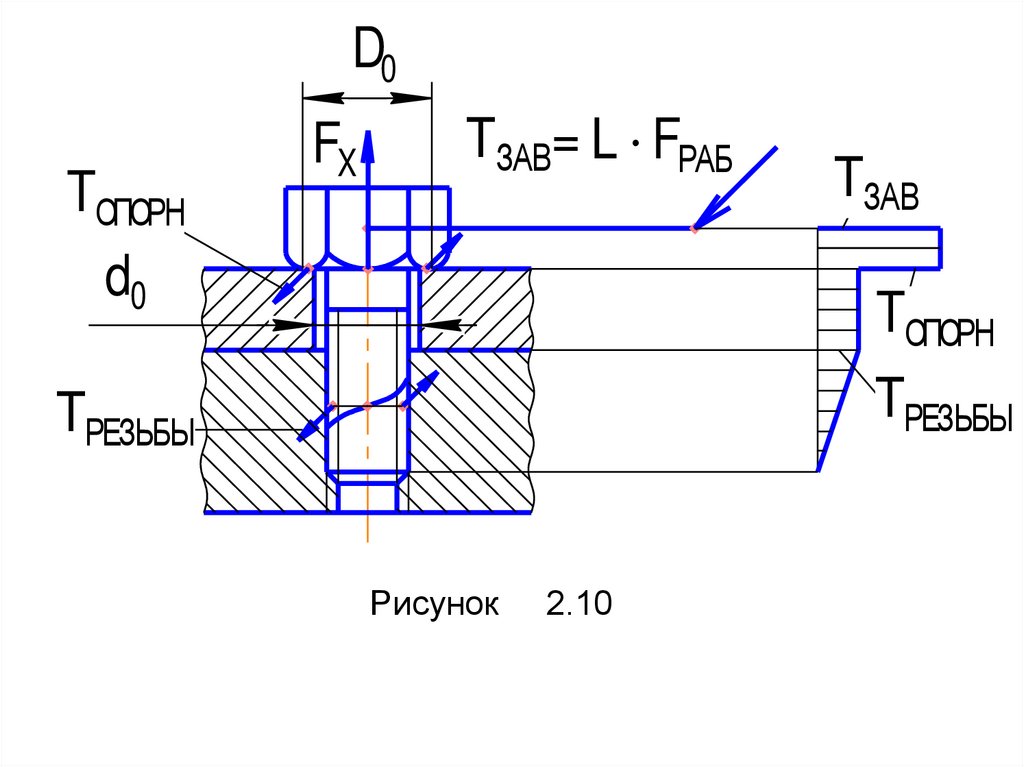
FX – осевая сила (сила тяжести груза,
поднимаемого
домкратом, согласно
рисунку 2.7, или сила затяжки винта, по
рисунку 2.10);
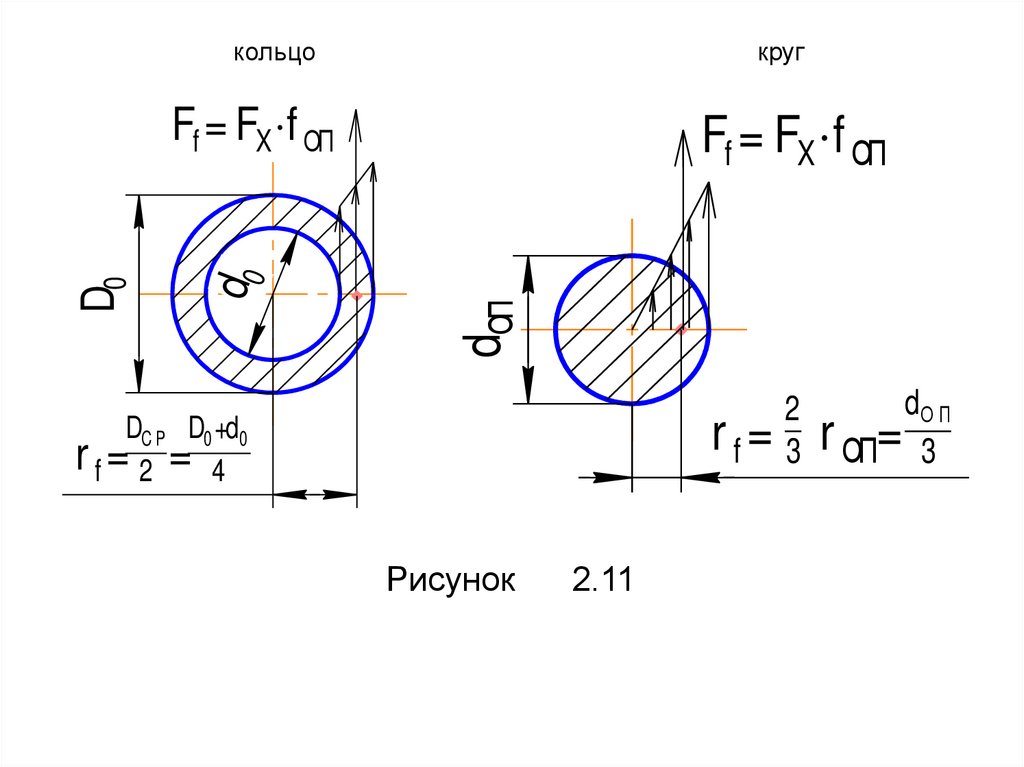
rf – радиус трения (в зависимости от формы
опорной поверхности находится согласно
рисунку 2.11);
F
L T
T
ЗАВ
РАБ
РЕЗЬБЫ
ОПОРН
d2
FX tg ( ) FX fОП rf
2
Т

7.

D0
TОПОРН
d0
FX
ТЗАВ= L FРАБ
ТЗАВ
TОПОРН
ТРЕЗЬБЫ
ТРЕЗЬБЫ
Рисунок
2.10

8.

кольцо
круг
Ff = FX f ОП
dОП
d0
D0
Ff = FX f ОП
dО П
2
r f = 3 r ОП= 3
DC P D0 +d0
rf= 2 = 4
Рисунок
2.11

9.

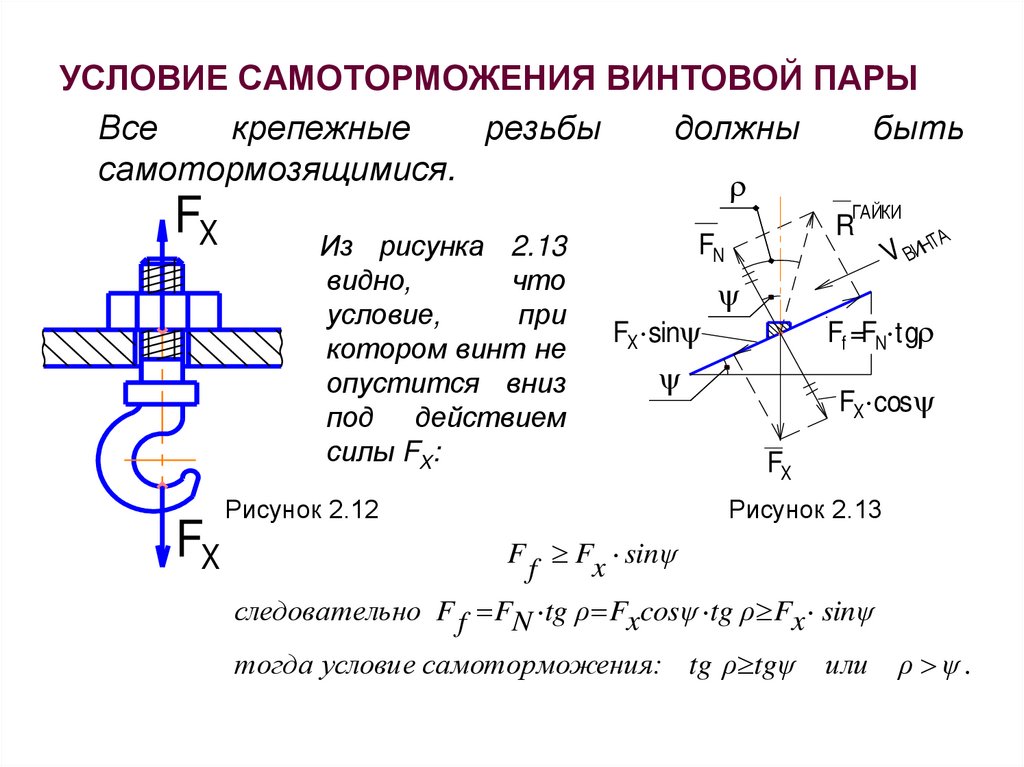
УСЛОВИЕ САМОТОРМОЖЕНИЯ ВИНТОВОЙ ПАРЫ
Все
крепежные
резьбы
должны
быть
самотормозящимися.
FX
FX
ГАЙКИ
Из рисунка 2.13
видно,
что
условие,
при
котором винт не
опустится вниз
под действием
силы FX:
Рисунок 2.12
R
FN
FX sin
А
V ВИНТ
Ff =FN tg
FX cos
FX
Рисунок 2.13
F Fx sinψ
f
следовательно F f FN tg ρ Fxcosψ tg ρ Fx sinψ
тогда условие самоторможения: tg ρ tgψ
или
ρ ψ.

10.

Так как при вибрациях, из-за микроперемещений
деталей соединения, силу трения Ff в резьбе
сохранить сложно (сила FN может кратковременно
снизиться до нуля), необходимо предусмотреть
специальные средства стопорения резьбовых
соединений. На практике, чаще других, используют
два следующих способа:
1) поддержание небольшой силы трения на
поверхности витков резьбы, при исчезновении
затяжки болта при вибрациях, с помощью
дополнительной контрогайки
или упругой
пружинной шайбы;
2) исключение разворота гайки относительно болта
с
помощью
специальных
стопорящих
устройств.

11.

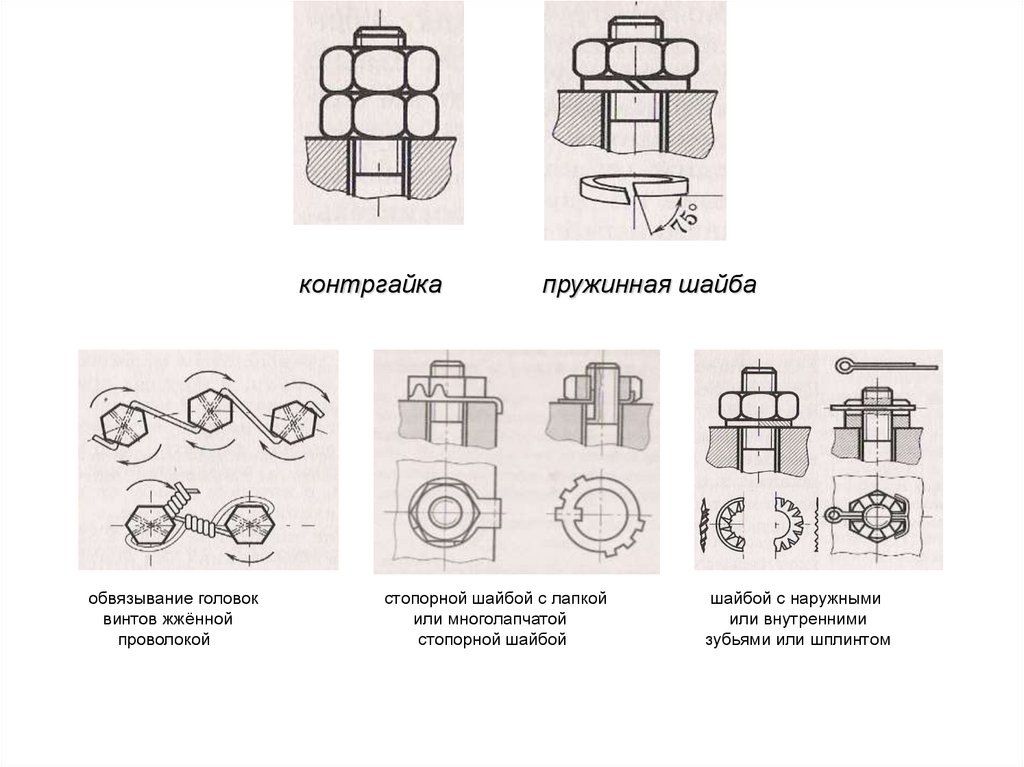
контргайка
обвязывание головок
винтов жжённой
проволокой
пружинная шайба
стопорной шайбой с лапкой
или многолапчатой
стопорной шайбой
шайбой с наружными
или внутренними
зубьями или шплинтом

12.

Ft2 РАБ
FX
d2
Ph
КПД ВИНТОВОЙ ПАРЫ
граница
самот орможения
d
=0
d
=
област ь работ ы
ходовых резьб
област ь работ ы
крепёжных резьб
0
45 - 2
Рисунок 2.14
Рисунок 2.15
КПД
Aполезн
Fx Ph
Fx tg
tg
- винтовой
Азатр
Ft 2 d 2 Fx tg tg
пары
В винтовых механизмах КПД должен быть как можно
больше. Поэтому для ходовых резьб ψ задают из
d
условия максимума КПД , решая уравнение:
0.
d
ρ
0
ψ ηmax 45
- условие максимума КПД
2

13.

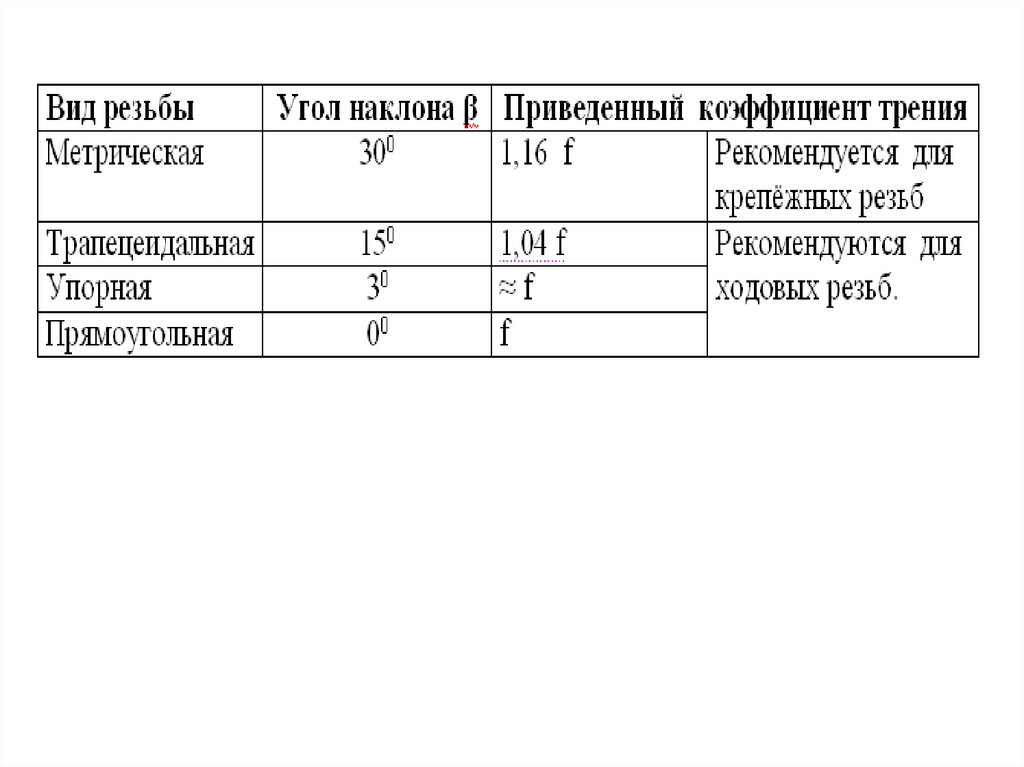
ПОНЯТИЕ О ПРИВЕДЕННОМ КОЭФФИЦИЕНТЕ ТРЕНИЯ
Все полученные выше формулы выведены для резьб с
прямоугольным профилем.
Ими можно воспользоваться и для непрямоугольных
резьб, только вместо угла трения ρ в формулу
необходимо подставлять ρ′ - приведенный угол
трения, а вместо f подставить f′ - приведенный
коэффициент трения.
Например,
при
вычислении
силы
трения
Ff
на
поверхности прямоугольной и трапецеидальной резьб:

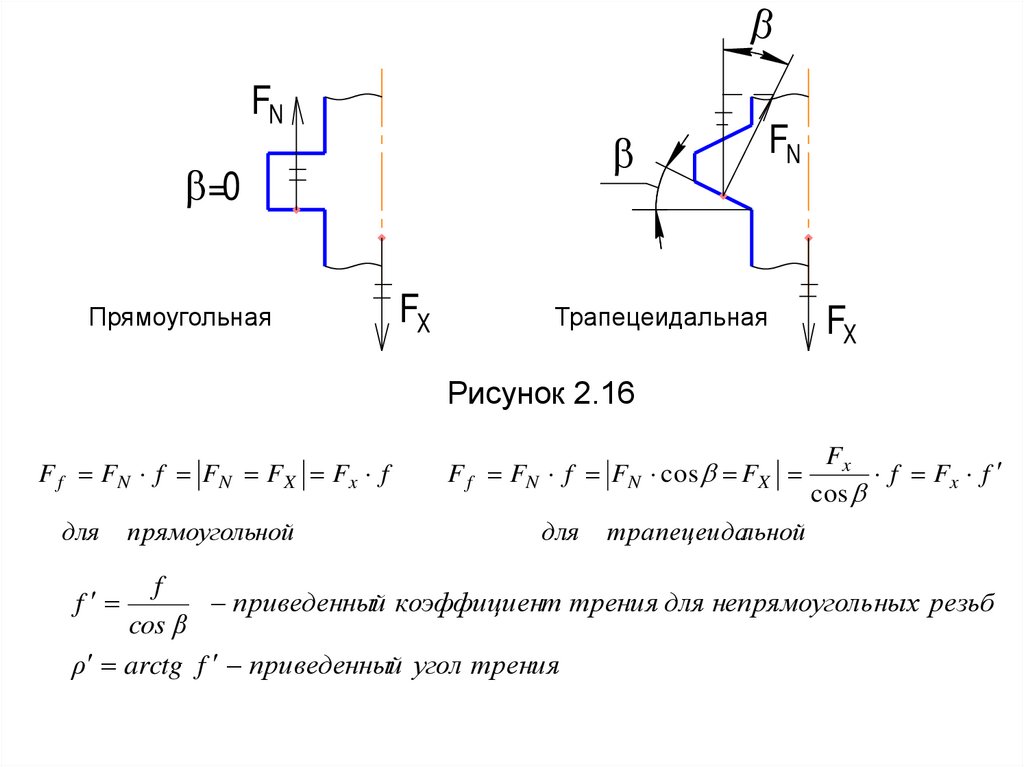
14.

FN
=0
Прямоугольная
FX
FN
Трапецеидальная
FX
Рисунок 2.16
F f FN f FN FX Fx f
для
прямоугольной
F f FN f FN cos FX
для
Fx
f Fx f
cos
трапецеидальной
f
приведенный коэффициент трения для непрямоугольных резьб
cos β
ρ arctg f приведенный угол трения
f