Similar presentations:
Многогранники. Основные понятия
1.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТКАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ГРАФИКИ
НАПРАВЛЕНИЕ «СТРОИТЕЛЬСТВО»
(БАКАЛАВРИАТ)
Москва 2015 г.
1
2.
23.
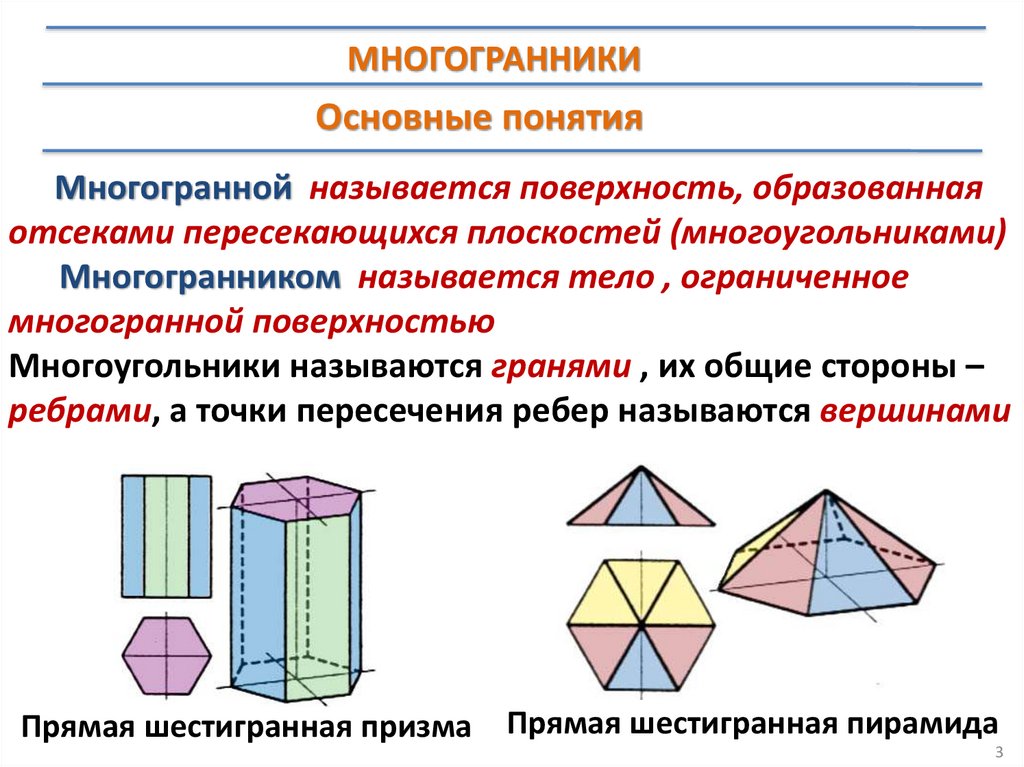
МНОГОГРАННИКИОсновные понятия
Многогранной называется поверхность, образованная
отсеками пересекающихся плоскостей (многоугольниками)
Многогранником называется тело , ограниченное
многогранной поверхностью
Многоугольники называются гранями , их общие стороны –
ребрами, а точки пересечения ребер называются вершинами
Прямая шестигранная призма Прямая шестигранная пирамида
3
4.
Правильные многогранникиНаименование
многогранников
Вид
граней
Число элементов
граней вершин
ребер
Граней,
сходящихся
в вершине
Четырехгранник
тетраэдр
Треугольник
4
4
6
3
Куб (шестигранник)
гексаэдр
Квадрат
6
8
12
3
Восьмигранник
октаэдр
Треугольник
8
6
12
4
Двенадцатигранник
додекаэдр
Пятиугольник
12
20
30
3
Двадцатигранник
икосаэдр
Треугольник
20
12
30
5
4
5.
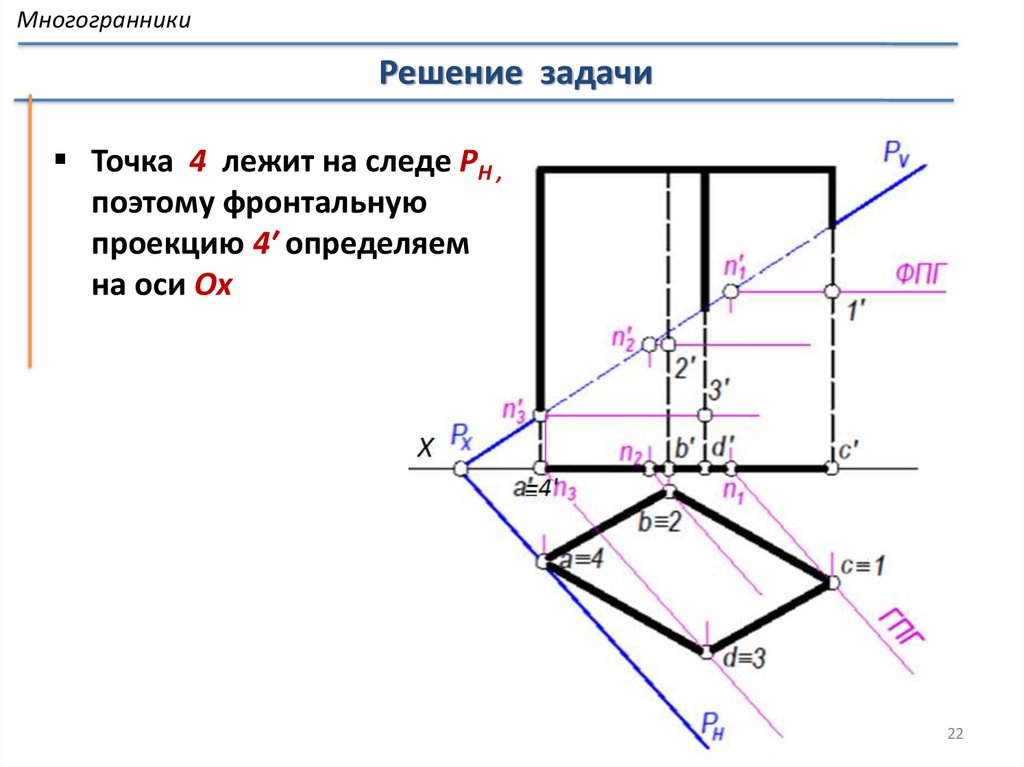
МногогранникиОбщие сведения
Точка на поверхности многогранника
По заданной горизонтальной проекции точки Е ,
принадлежащей грани пирамиды ABS , построены
фронтальная e' и профильная e" проекции
Через точку e проводим
прямую 1-2 , параллельно
стороне ab основания
Строим фронтальную
проекцию прямой 1'- 2'
(1'2' II a'b') , на которой по
линии связи отмечаем
точку e'
Аналогично находим
профильную проекцию e"
5
6.
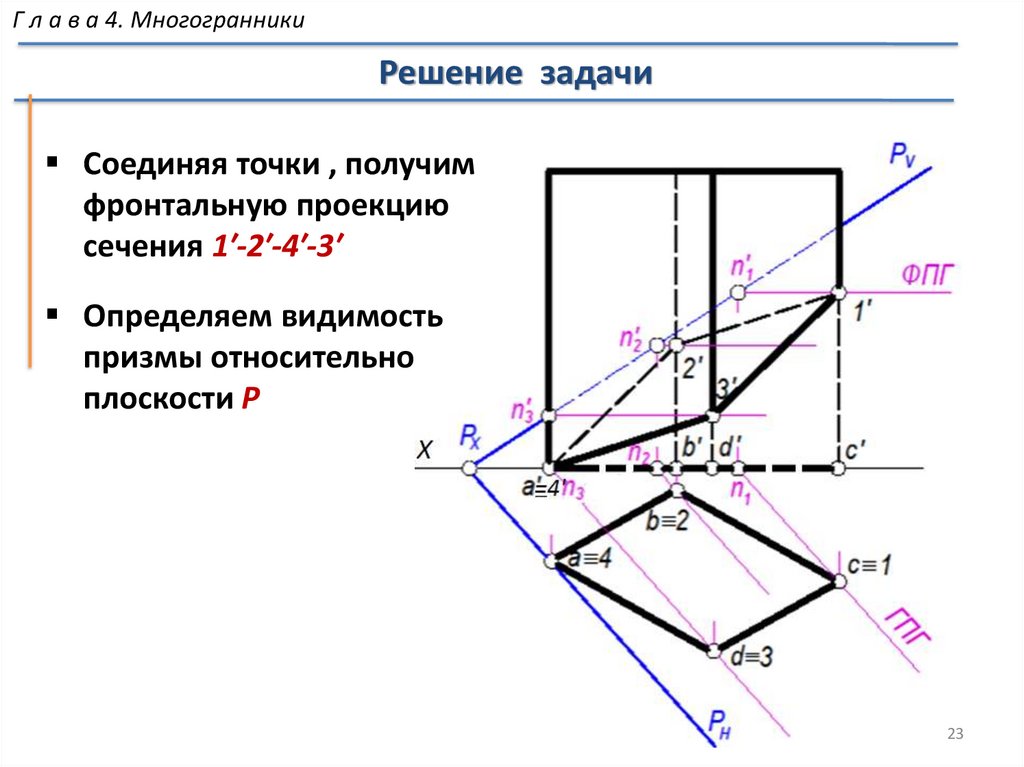
МногогранникиПересечение многогранника плоскостью
Основные понятия
При пересечении многогранника плоскостью
образуется замкнутая ломаная линия (многоугольник).
Плоская фигура, получаемая в результате пересечения,
называется сечением
Решение задачи сводится к многократному
пересечению прямой с плоскостью
Точки, в которых ребра многогранника пересекаются с
заданной плоскостью, будут вершинами искомого
сечения
6
7.
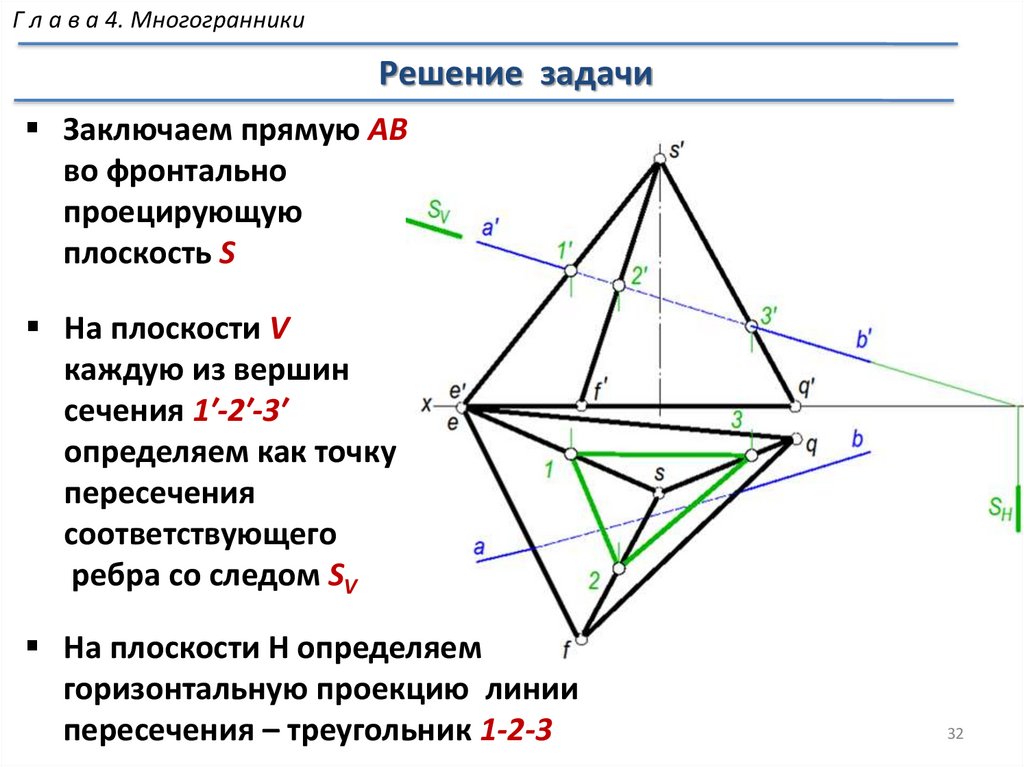
МногогранникиПересечение многогранника плоскостью
Пересечение многогранника проецирующей плоскостью
Если секущая плоскость проецирующая (то есть перпендикулярная
плоскости проекций) ,то построение линии пересечения (АВС)
упрощается , так как одна проекция этой линии (а′в′с′) совпадает со
следом секущей плоскости.
Задача сводится к построению недостающих проекций точек
а, в, с , которые определяются на проекциях соответствующих
7
ребер.
8.
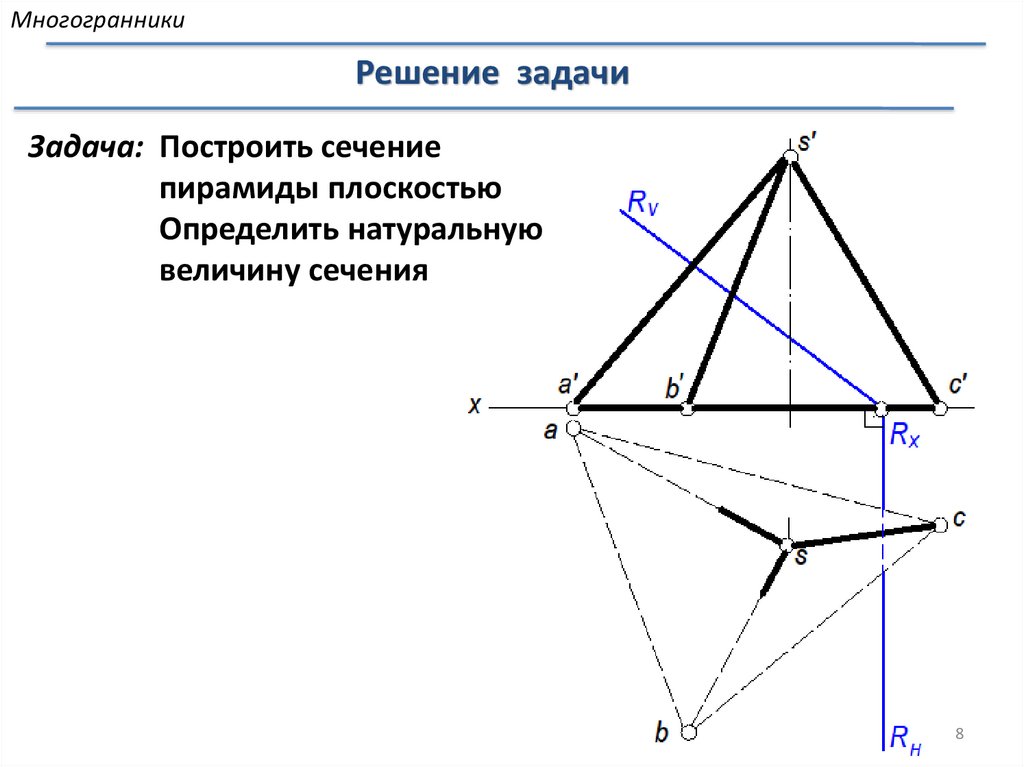
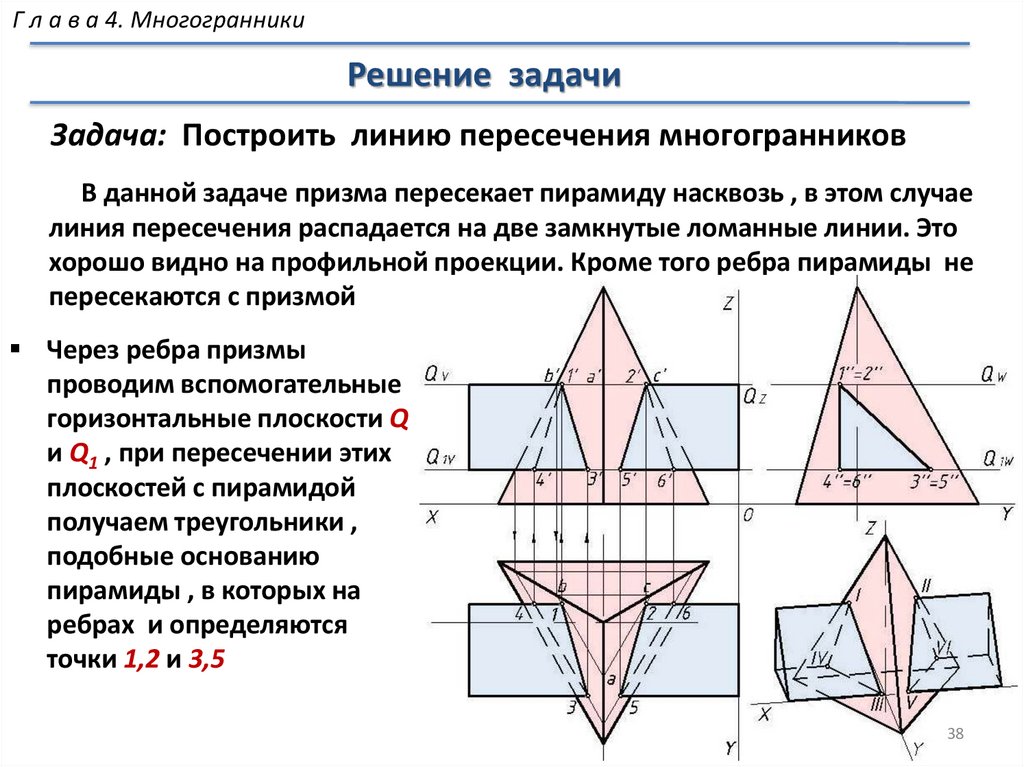
МногогранникиРешение задачи
Задача: Построить сечение
пирамиды плоскостью
Определить натуральную
величину сечения
8
9.
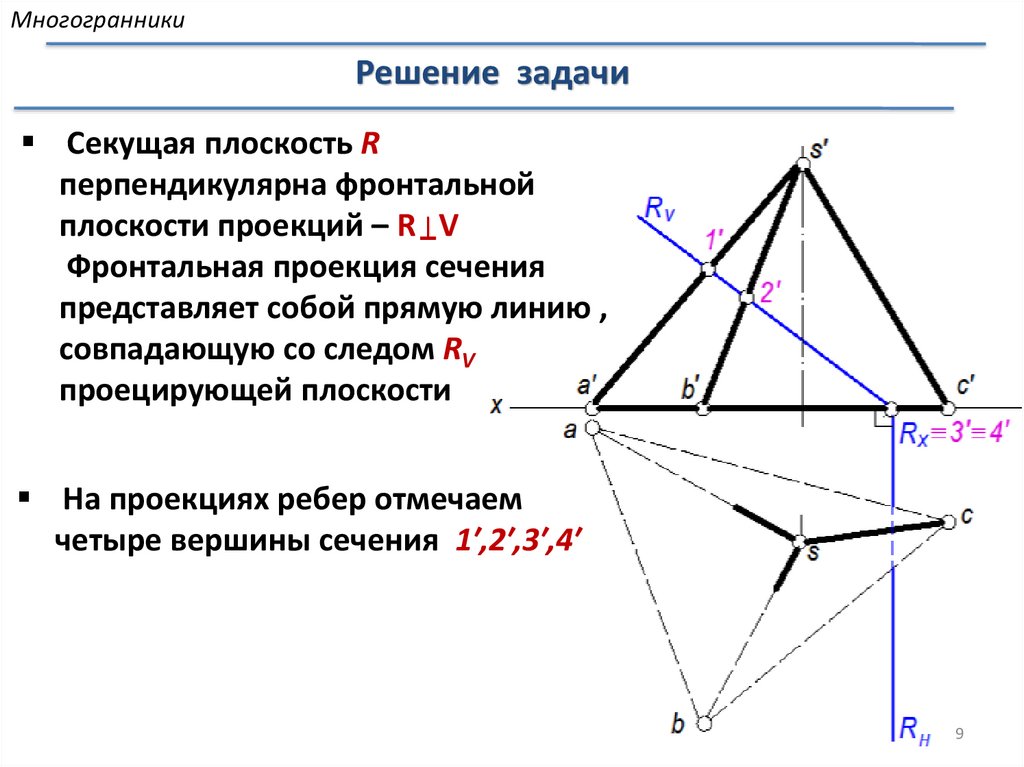
МногогранникиРешение задачи
Секущая плоскость R
перпендикулярна фронтальной
плоскости проекций – R V
Фронтальная проекция сечения
представляет собой прямую линию ,
совпадающую со следом RV
проецирующей плоскости
На проекциях ребер отмечаем
четыре вершины сечения 1′,2′,3′,4′
9
10.
МногогранникиРешение задачи
Каждую из вершин сечения ,
отмеченную на фронтальной
плоскости проекций 1′,2′,3′,4′,
находим на горизонтальной
проекции - 1,2,3,4
10
11.
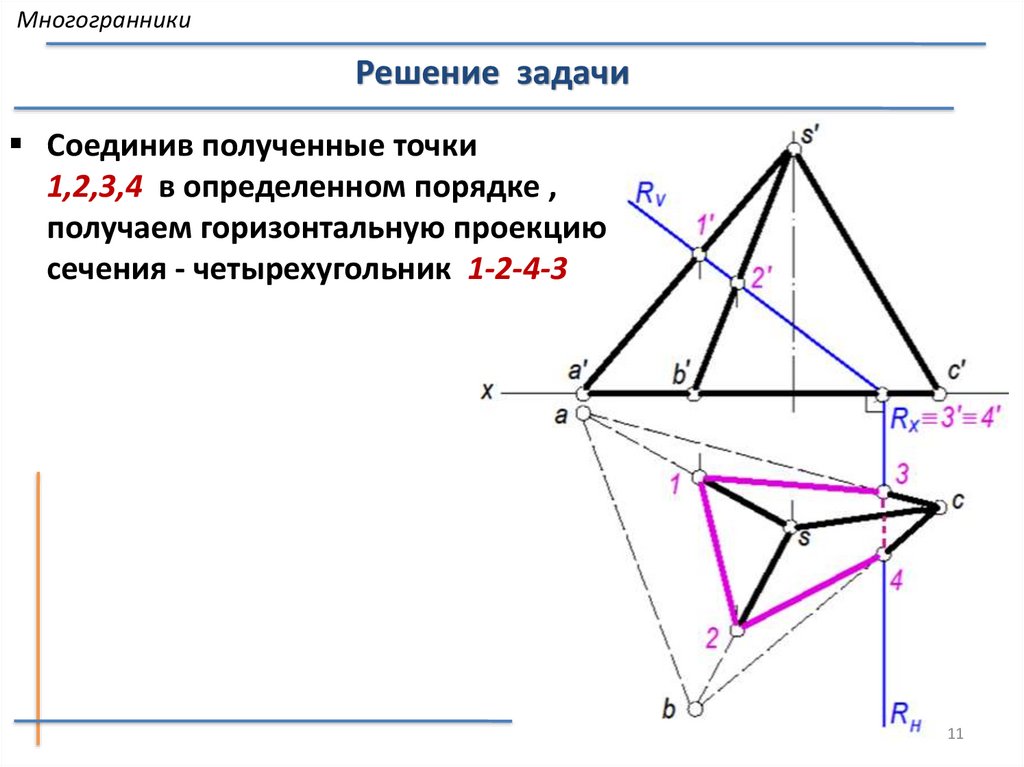
МногогранникиРешение задачи
Соединив полученные точки
1,2,3,4 в определенном порядке ,
получаем горизонтальную проекцию
сечения - четырехугольник 1-2-4-3
11
12.
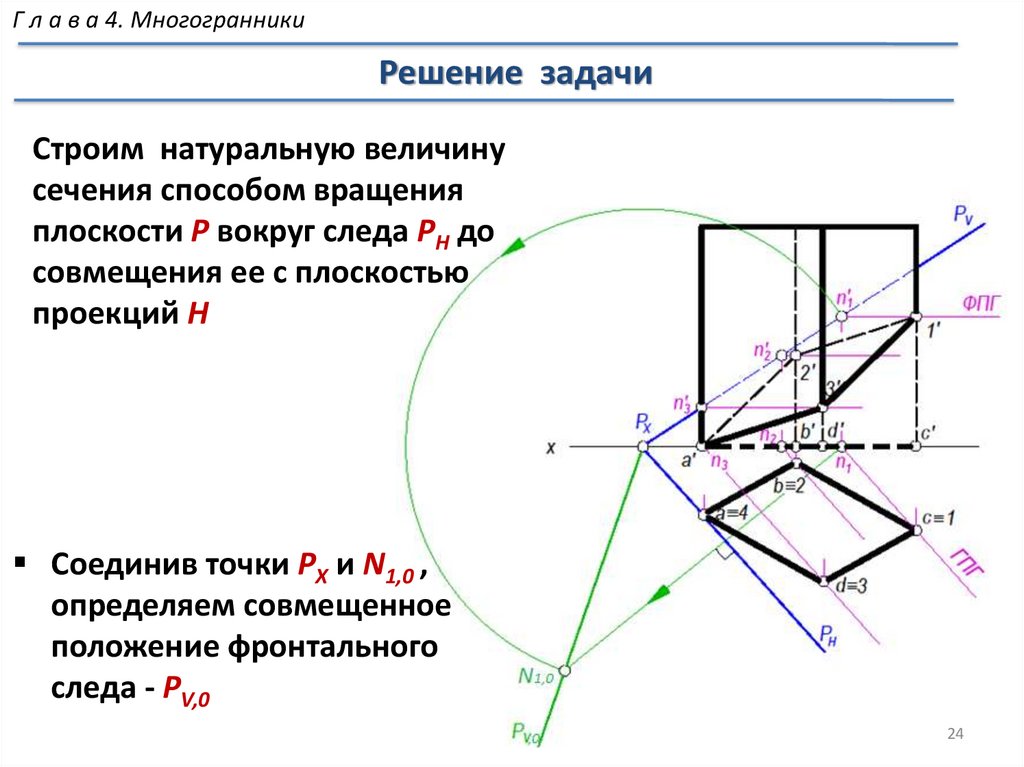
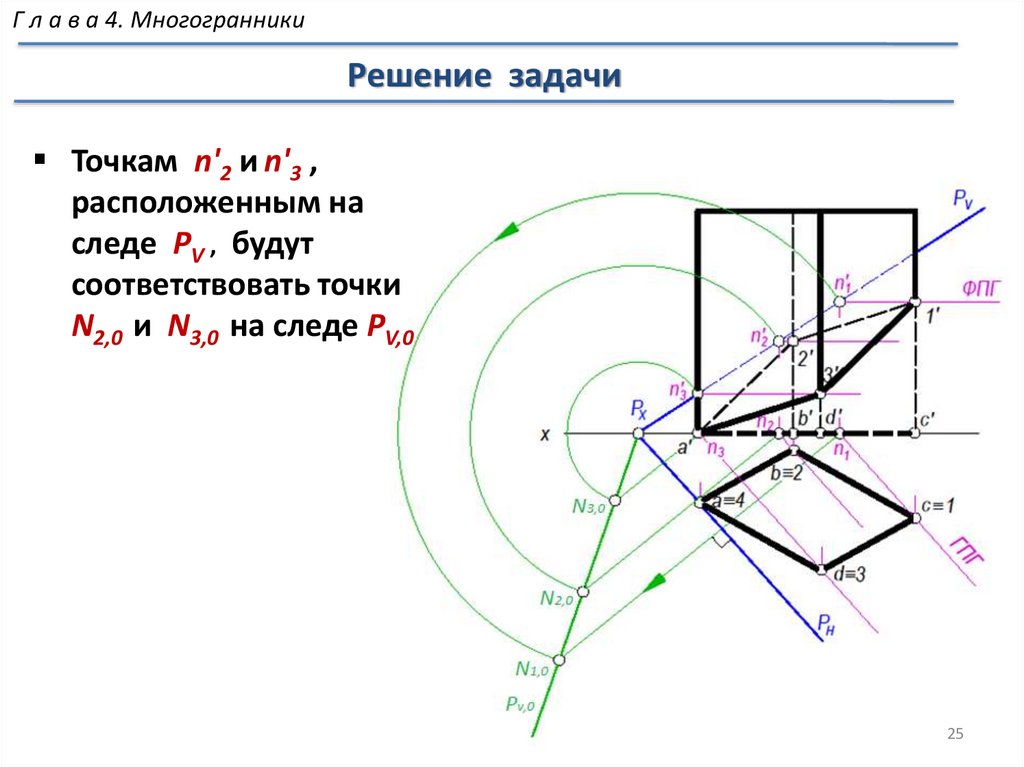
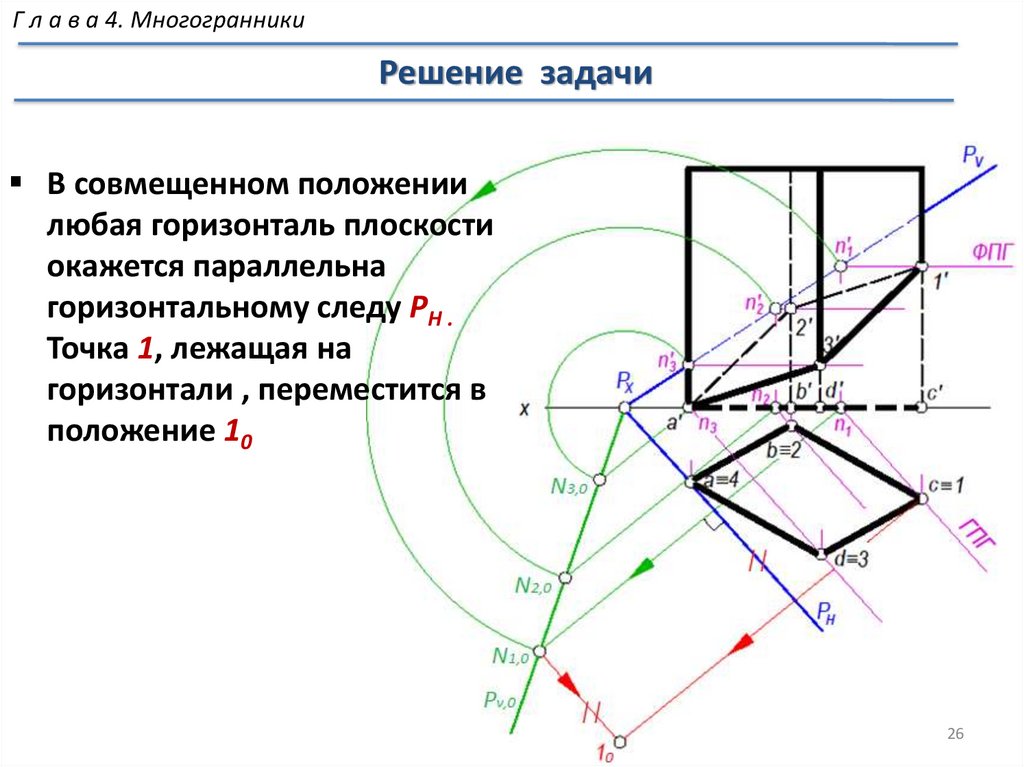
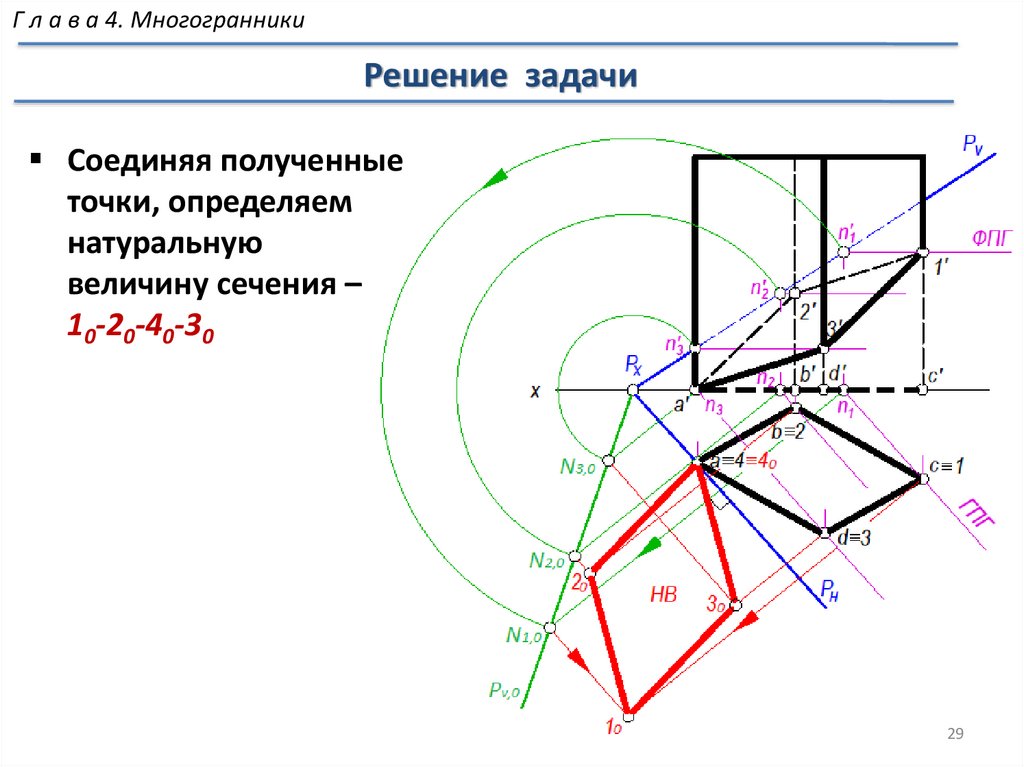
МногогранникиРешение задачи
Проекции сечения не определяют
действительные размеры сечения ,
так как секущая плоскость не
параллельна ни одной из
плоскостей проекций
Строим натуральную
величину сечения 10-20-30-40
способом совмещения
12
13.
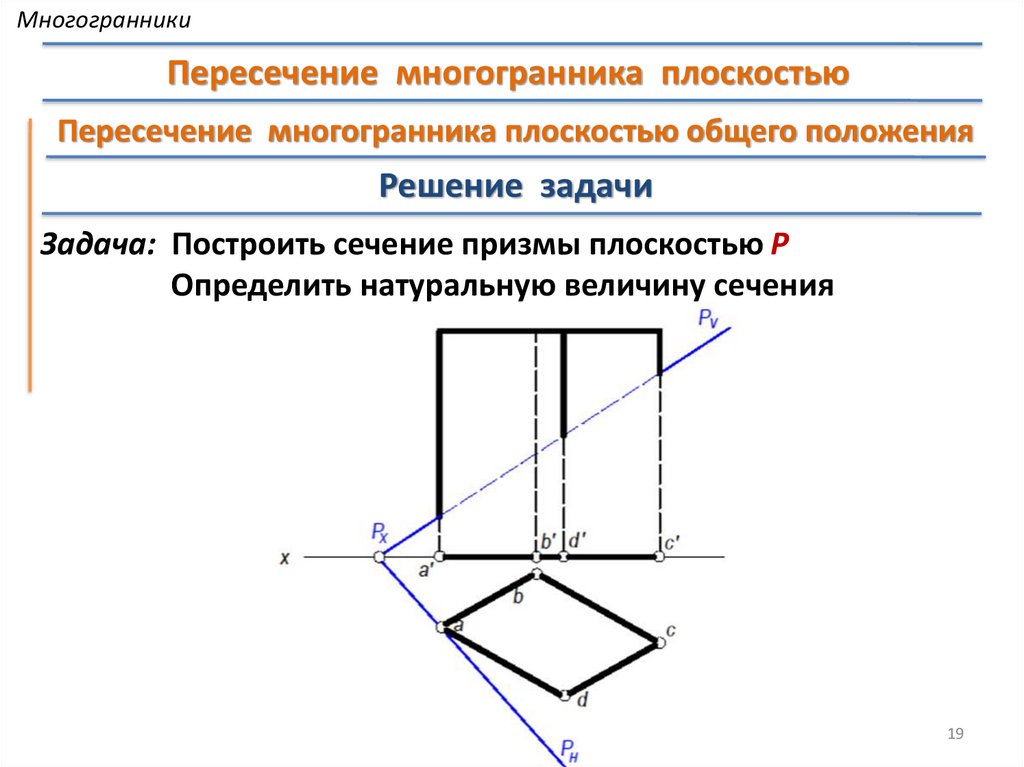
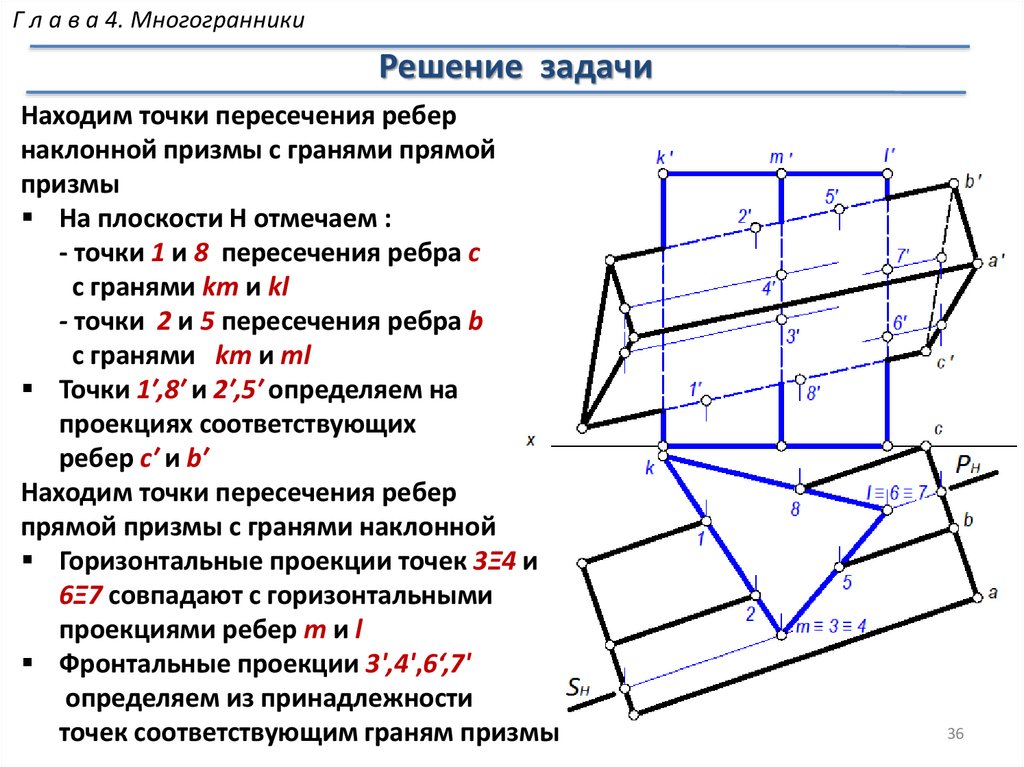
МногогранникиРешение задачи
Задача: Построить сечение призмы плоскостью
Определить натуральную величину сечения
13
14.
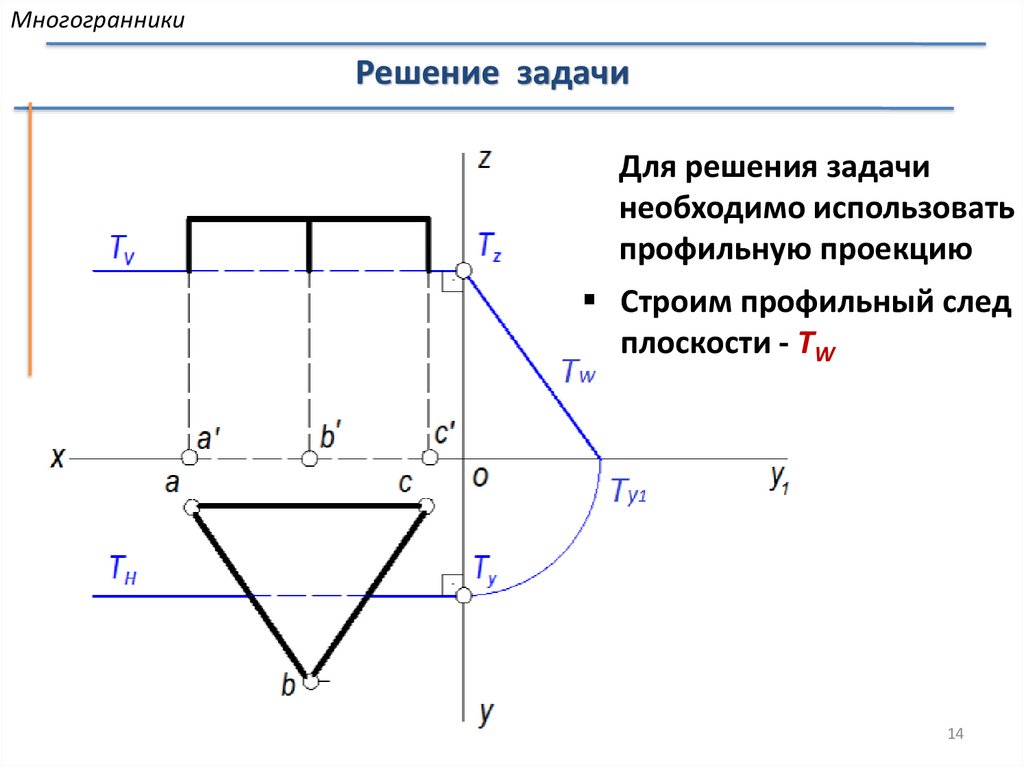
МногогранникиРешение задачи
Для решения задачи
необходимо использовать
профильную проекцию
Строим профильный след
плоскости - TW
14
15.
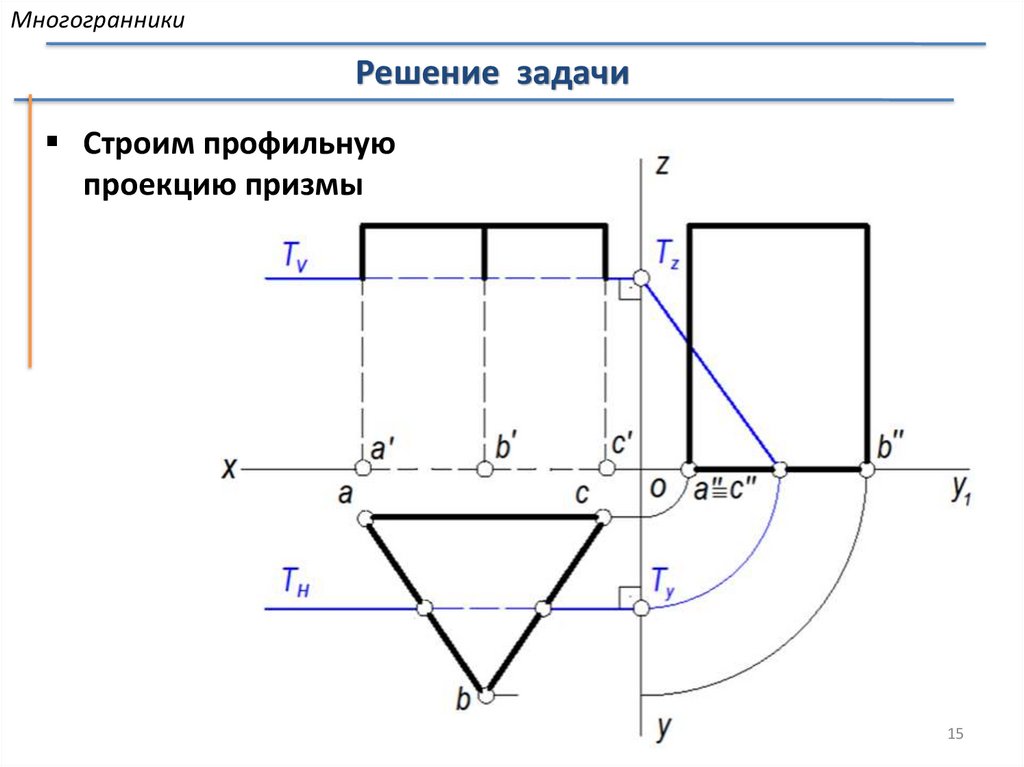
МногогранникиРешение задачи
Строим профильную
проекцию призмы
15
16.
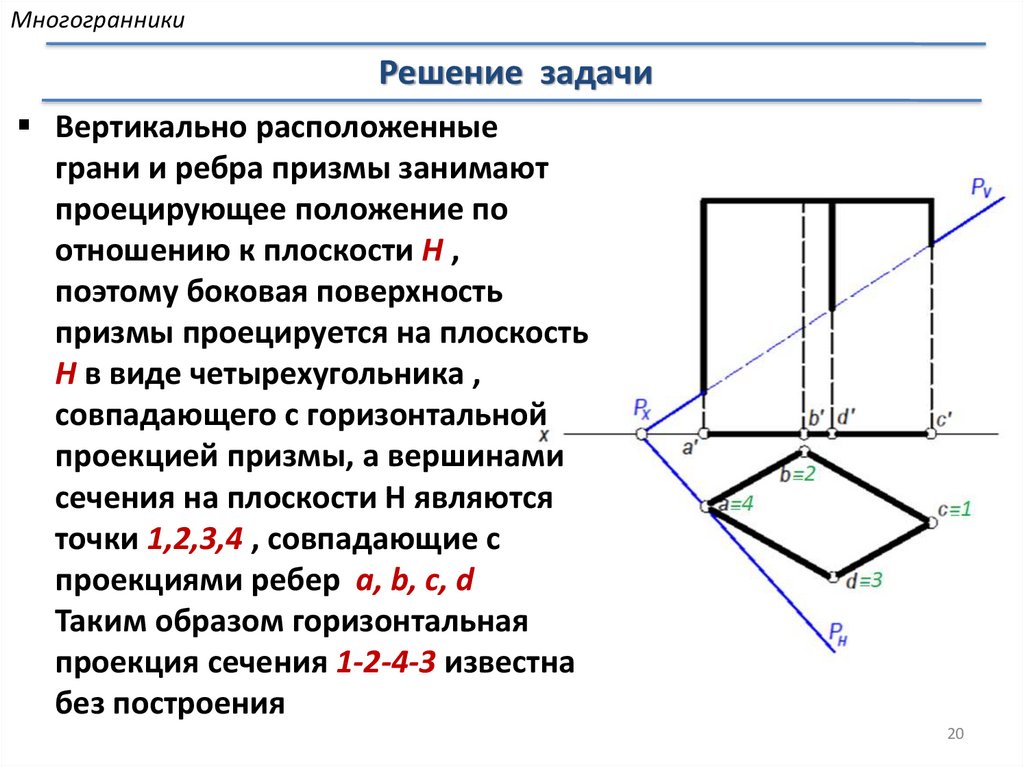
МногогранникиРешение задачи
Секущая плоскость T перпендикулярна профильной плоскости
проекций, следовательно профильная проекция сечения
совпадает со следом TW проецирующей плоскости
Находим четыре
вершины сечения как
точки пересечения
соответствующих ребер
с заданной плоскостью Т
16
17.
МногогранникиРешение задачи
Соединяем полученные точки в определенном порядке ,
получаем горизонтальную и фронтальную проекции
сечения
17
18.
МногогранникиРешение задачи
Строим натуральную
величину сечения
способом перемены
плоскостей проекций





















 drafting
drafting








