Similar presentations:
Смешанные вычисления
1.
Смешанные вычисления• Упростить
выражение при
x = -1.5
1. Что доступно, а что
задержано?
2. Константные
вычисления
3. Дополнительные
«улучшения»
2
2
x +y
2 xy
2
2.25+y
−
3y
2.
Почему «смешанные»?• В процессе смешанного выполнения
обычные вычисления чередуются
(«смешиваются») с преобразованием
программы.
• Другие имена: частичные вычисления,
partial evaluation, partial computation,
специализация, суперкомпиляция.
3.
Программы как данныеМножество данных D,
такое что DxD D (пара данных тоже
данные, те можно конструировть данные из данных)
• Множество программ P D
• Семантика программы (язык) :
L : P (D D)
• Обозначение:
• L(p) = [p]L
• [p]L = [p], если понятно, для какого L
4.
Основное уравнение СВОпределение. Пусть p – программа в
языке L получает на вход пару
аргументов(данные):
[p](x,y) = res
Проекцией программы p на значение
первого аргумента x называется
программа px, такая что для любого y
[p](x,y) = [px]y (??)
5.
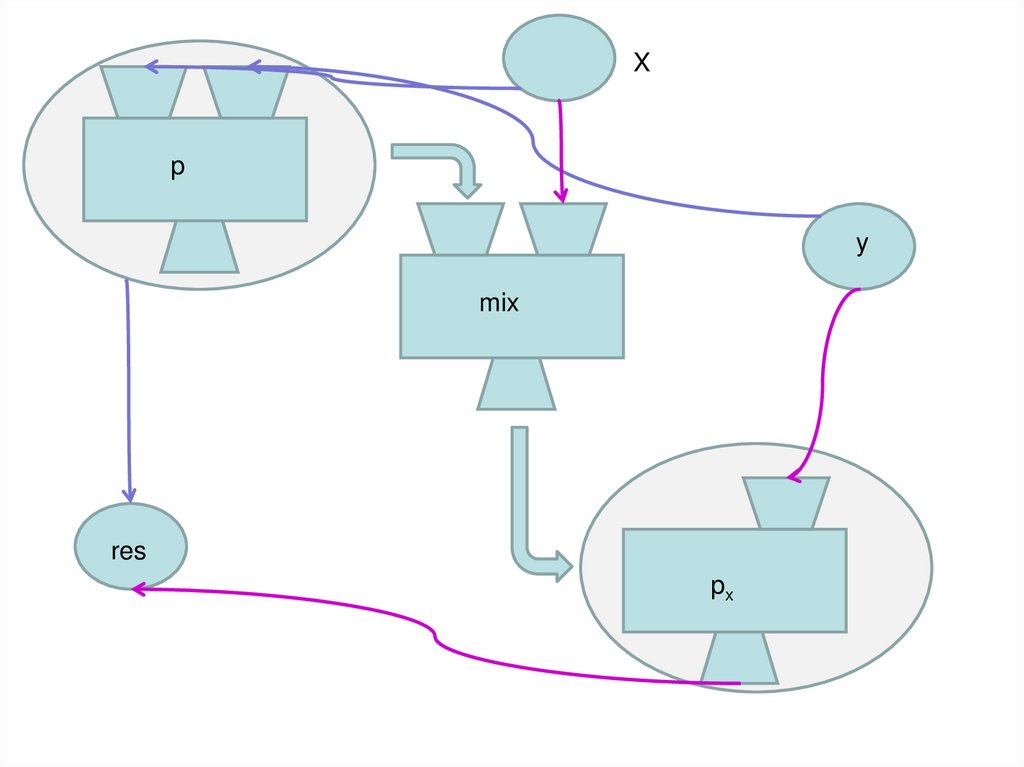
Основное уравнение СВ• Смешанный вычислитель mix –
программа в языке I, такая что
[mix]I (p,x) = px
Таким образом,
(основное уравнение)
[[mix]I (p,x)]L y = [p]L (x,y)
6.
Xp
y
mix
res
px
7.
S-m-n теорема КлиниТеорема. Пусть Un(x0,x1,…,xn) –
универсальная функция. Тогда для
любых n и m (n,m>0) существует
общерекурсивная snm(x0,x1,…,xm), такая
что для любой f(x1,…,xm+n) c номером Nf
имеет место
f(x1,…,xm+n) = Un+m(Nf, x1,…,xm+n) =
= Un(snm(Nf,x1,…,xm), xm+1,…, xm+n)
8.
S-m-n теорема Клини• f(x1,…,xm+n) = Un+m(Nf, x1,…,xm+n) =
= Un(snm(Nf,x1,…,xm), xm+1,…, xm+n)
• Подставим
• f = [p]
• Nf = p
• snm = [mix]I
• x1,…, xm = x
• xm+1,…xm+n = y
• Un = Un+m =[intL] : [intL](p,d) = [p]d
[p](x,y) = [intL](p, (x, y)) =
[intL]([mix]I(p,x),y)
9.
Когда это выгодно?Обозначение.T(p,d) – время работы p на
данных d.
Пусть n – количество исполнений p. Тогда
должно выполняться
nT ( p,( x,y))≥ T ( mix,( p,x))+nT ( p x ,y)
T (mix,( p,x))
Px оптимизированная
n≥
T ( p,( x,y))− T ( p x ,y) программа
10.
СВ и трансляцияОпределение. int - интерпретатор
языка L, записанный в языке I, если для
любых p,d
[int]I(p,d) = [p]Ld
Определение. comp - транслятор с
языка L в язык I, записанный в языке I,
если для любых p,d
[ [comp]Ip ]I d = [p]Ld
[comp]Ip – объектный код.
11.
Первая проекция Футамурыавтор
• Предположим, что мы собираемся
многократно интерпретировать (то есть
применять int) одну и ту же программу –
хороший повод специализировать
интерпретатор для этой программы
[intp]I d =
= [[mix]I(int,p)]I d = по осн. ур.
смеш выч. p = int, x = p
= [int]I(p,d) =
= [p]L d
12.
Вторая проекция Футамуры• Предположим, что мы собираемся
многократно специализировать один и тот же
интерпретатор для разных программ –
хороший повод специализировать
специализатор для этого интерпретатора
[mixint]I p =
= [[mix]I(mix,int)]I p =
= [mix]I(int,p) =
= intp
• mixint – транслятор, intp – объектный код.
Транс с яз интерпр на язык программы
13.
Третья проекция Футамуры• Предположим, что мы собираемся
многократно специализировать один и тот же
специализатор для разных интерпретаторов –
хороший повод специализировать
специализатор для этого интерпретатора
[mixmix]I int =
= [[mix]I(mix,mix)]I int =
= [mix]I(mix,int) =
= mixint
• mixmix – генератор трансляторов.
14.
Четвёртая проекцияФутамуры?
• Генератор трансляторов воспроизводит
собственный текст (с точн до эквив)
[mixmix]I mix =
= [[mix]I(mix,mix)]I mix =
= [mix]I(mix,mix) =
= mixmix
• Генератор трансляторов mixmix – транслятор
для «интерпретатора» mix. «Объектный код»
[mixp]x = [mix](p,x) = px
- генерирующее расширение.
15.
Метаинтерпретаторы• int01 – интерпретатор L1 записанный в L0
• int12 – интерпретатор L2 записанный в L1
• Исполнение программы p из L2 при
наличии исполнителя для L0:
[int01]L0(int12,(p,d)) =
= [int12]L1(p,d) =
= [p]L2d
• Сложность?
16.
Метаинтерпретаторы[[mix]I (int01,int12)]L0 (p,d) =
= [int01]L0 (int02,(p,d)) =
= [int12]L1 (p,d) =
= [p]L2 d
[mix]I (int01,int12) – интерпретатор L2,
записанный в L0.
17.
Автоинтерпретатор• Пусть int - интерпретатор L0,
записанный в L0, тогда для любой
программы p из L0
[intp]L0 = [p]L0
• Рассмотрим p1, p2, p3, …где
p1 = p
pi+1 = [mix](int,pi)
• Критерий оптимальности Джонса
(N.Jones): p2=p3=p4=…
18.
Другие приложения1. Синтаксически-ориентированные
анализаторы:
[UniversalParser](Grammar, Tokens)
[mix] (UniversalParser, Grammar) =
= UniversalParserGrammar
- специализированный анализатор.
19.
Другие приложения2. Поиск по образцу:
[UniversalMatcher](Pattern, String)
[mix] (UniversalMatcher, Pattern) =
= UniversalMatcherPattern
- специализированный поиск.
20.
Другие приложения3. Машинная графика:
[RayTracer](Scene, ViewPoint)
[mix] (RayTracer, Scene) =
= RayTracerScene
- «обзор» фиксированной сцены с
различных точек.
21.
Подходы к реализации• «Интерпретационный» подход:
реализуем смешанный вычислитель mix
[mix] (p,x) = px
• «Трансляционный» подход: реализуем
генерирущий расширитель cogen
эквивалентны mixmix
[[cogen] p] x = px
22.
xnread(x)
read(n)
y := 1
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
23.
Интерпретационный подходread(x)
read(n)
y := 1
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
Действие
Рез-т
read(x)
x
dx
y
dy
n
dn
Ост. прогр.
#
false
?
true
?
true
read(x)
3
true
2
true
read(n)
y:=1
1
n>0
true
even(n)
false
true
n := n-1
y :=y*x
#
n>0
true
even(n)
true
false
n:=n/2
1
x:= x*x
#
n>0
true
even(n)
false
x:= x*x
0
y :=y*x
write(y)
true
false
n := n-1
n>0
y:=1*x
#
false
true
y:=y*x
false
write(y)
24.
Генерирующее расширениеread(x)
read(n)
y := 1
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
writeln(“read(x)”); dx := false
read(n); dn := true;
y := 1; dy := true;
while n > 0 do
if even(n) then
if dn then n := n/2 else writeln(“n:=n/2”) fi;
if dx then x := x*x else writeln(“x:=n*x”) fi;
else
if dn then n := n-1 else writeln(“n:=n-1”) fi;
if dx and dy then
y := y*x
elseif dx then
writeln(“y := y*” + x);
elseif dy then
writeln(“y := “ + y + “*x”);
else
writeln(“y := y*x”);
fi
dy := dy and dx;
fi
od
if dy then write(y) else writeln(“write(y)”) fi
25.
Трансформационный подход• Редукция доступного ввода:
read(n)
=> n := c
где с – литеральное представление
доступного аргумента
• Редукция цикла
while E do S od
=> if E then S; while E do S od fi
• Редукция условного
if true then S1 else S2 fi => S1
if false then S1 else S2 fi => S2
26.
Трансформационный подход• Просачивание констант: (замена термов)
если в некоторой точке программы при
любом исполнении значение переменной
равно с, то использование переменной может
быть заменено на литеральное
представление c
• Редукция выражений(треб знан интерприи): если в выражении используются только
константы, то оно может быть заменено на
литеральное представление результата
27.
Трансформационный подход• Удаление неиспользуемых вычислений:
если результат присваивания нигде не
используется, то оно может быть удалено
(есть аналогия со схемным подходом)
28.
ПримерРедукция доступного ввода:
read(x)
read(n)
y := 1
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
read(x)
n := 3
y := 1
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
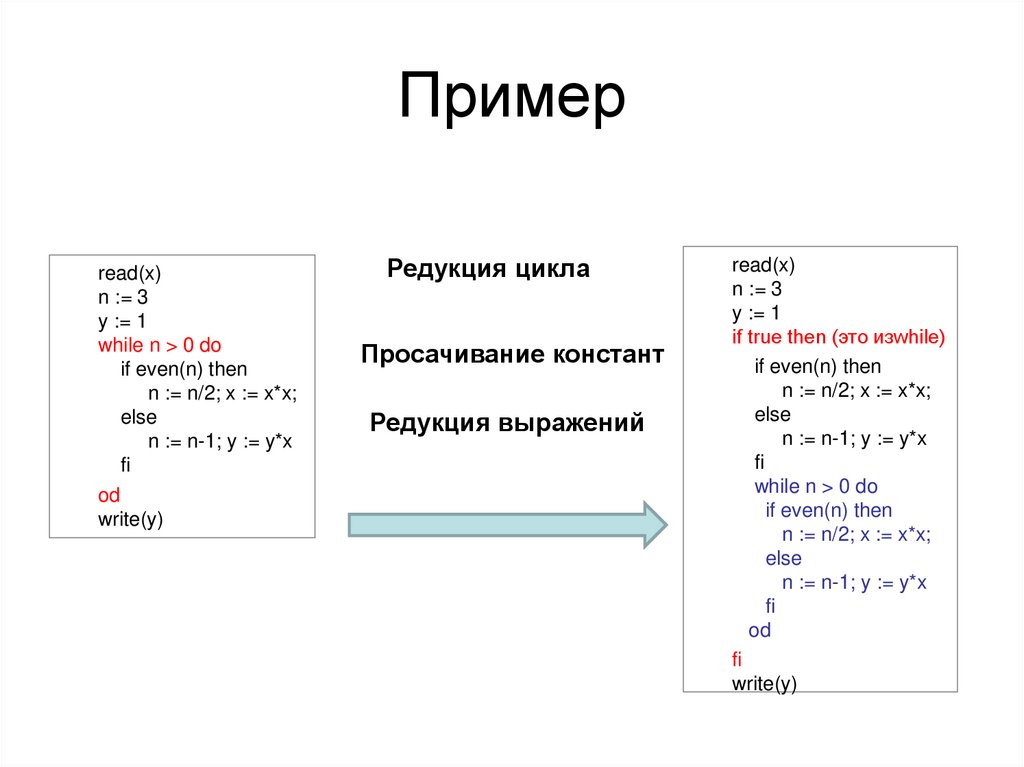
29.
Примерread(x)
n := 3
y := 1
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
Редукция цикла
Просачивание констант
Редукция выражений
read(x)
n := 3
y := 1
if true then (это изwhile)
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
fi
write(y)
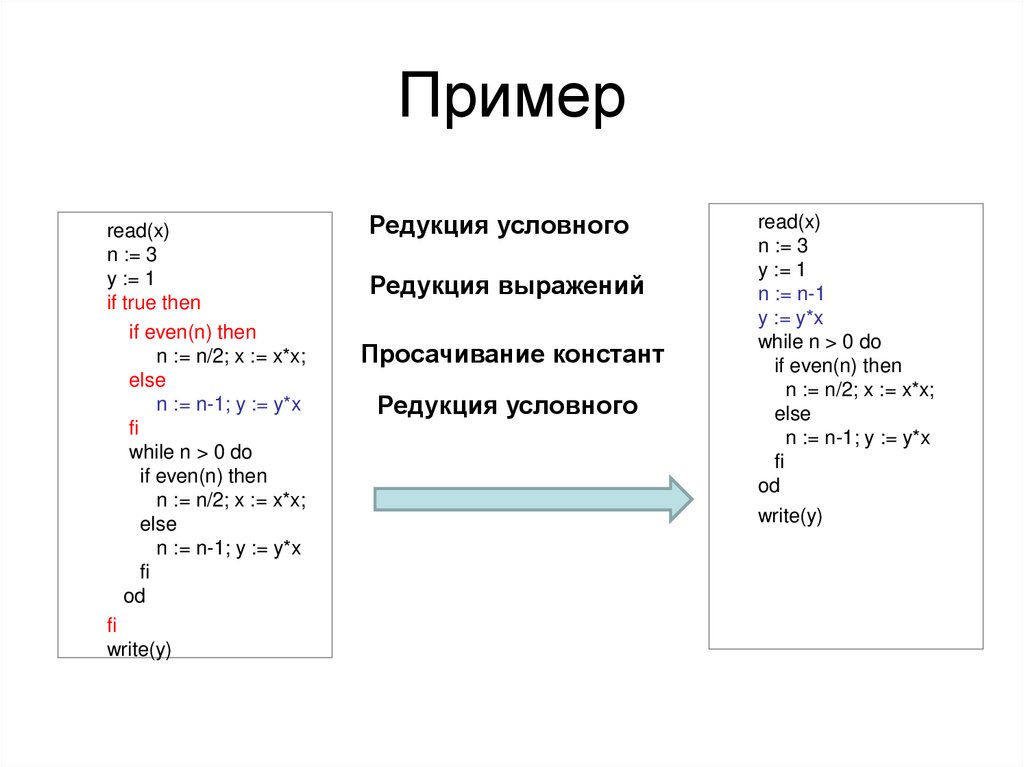
30.
Примерread(x)
n := 3
y := 1
if true then
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
fi
write(y)
Редукция условного
Редукция выражений
Просачивание констант
Редукция условного
read(x)
n := 3
y := 1
n := n-1
y := y*x
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
31.
Примерread(x)
n := 3
y := 1
n := n-1
y := y*x
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
Просачивание констант
Редукция выражений
Удаление неиспользуемых
read(x)
n := 2
y := 1*x
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
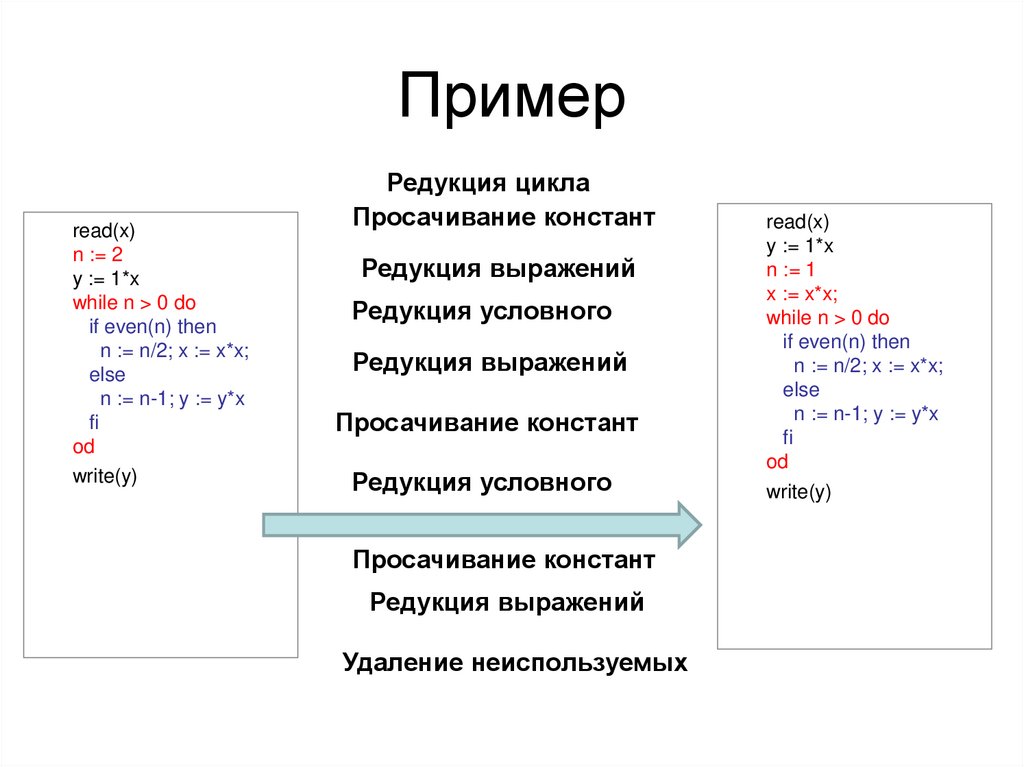
32.
Примерread(x)
n := 2
y := 1*x
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
Редукция цикла
Просачивание констант
Редукция выражений
Редукция условного
Редукция выражений
Просачивание констант
Редукция условного
Просачивание констант
Редукция выражений
Удаление неиспользуемых
read(x)
y := 1*x
n := 1
x := x*x;
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
33.
Примерread(x)
y := 1*x
n := 1
x := x*x;
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
Редукция цикла
Просачивание констант
Редукция выражений
Редукция условного
Редукция выражений
Просачивание констант
Редукция условного
Просачивание констант
Редукция выражений
Удаление неиспользуемых
read(x)
y := 1*x
x := x*x;
n := 0
y := y*x
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
34.
Примерread(x)
y := 1*x
x := x*x;
n := 0
y := y*x
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
write(y)
Редукция цикла
Просачивание констант
Редукция выражений
read(x)
y := 1*x
x := x*x;
n := 0
y := y*x
if false then
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
fi
write(y)
35.
ПримерРедукция условного
read(x)
y := 1*x
x := x*x;
n := 0
y := y*x
if false then
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
while n > 0 do
if even(n) then
n := n/2; x := x*x;
else
n := n-1; y := y*x
fi
od
fi
write(y)
Удаление неиспользуемых
read(x)
y := 1*x
x := x*x;
y := y*x
write(y)
Здесь мы могли редуцировать read(x)
услоаные операторы
write(x*(x*x))
36.
Задержанное управлениеДействие
read(x)
read(n)
if x > 0 then
n := n-1
else
n := n+1
fi
write(n)
Рез-т
read(x)
x
dx
y
dy
n
dn
Ост. прогр.
#
false
?
true
?
true
read(x)
3
true
#
false
read(n)
y:=1
x>0
write(n)
1
#
true
n:=3
if x > 0 then
n := 2
else
n := 4
fi
write(n)
• Экспликация доступной памяти
(n:=3)
• Задержка всех результатов
оператора (n:=2, n:=4)
37.
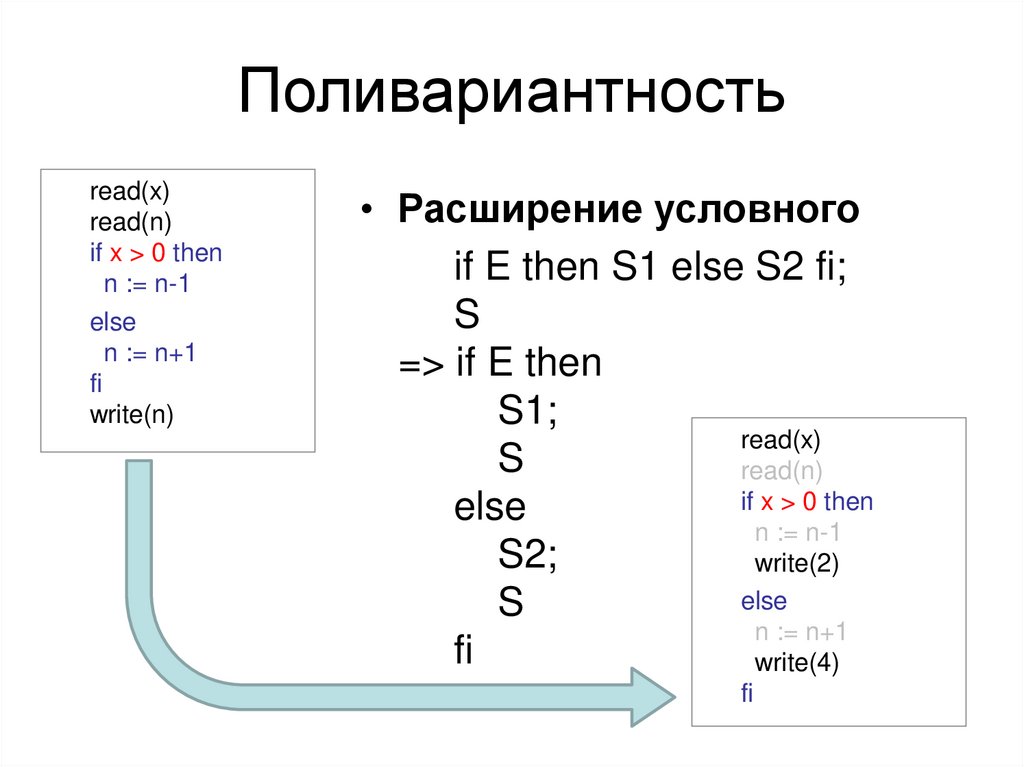
Поливариантностьread(x)
read(n)
if x > 0 then
n := n-1
else
n := n+1
fi
write(n)
• Расширение условного
if E then S1 else S2 fi;
S
=> if E then
S1;
read(x)
S
read(n)
if x > 0 then
else
n := n-1
S2;
write(2)
else
S
n := n+1
fi
write(4)
fi
38.
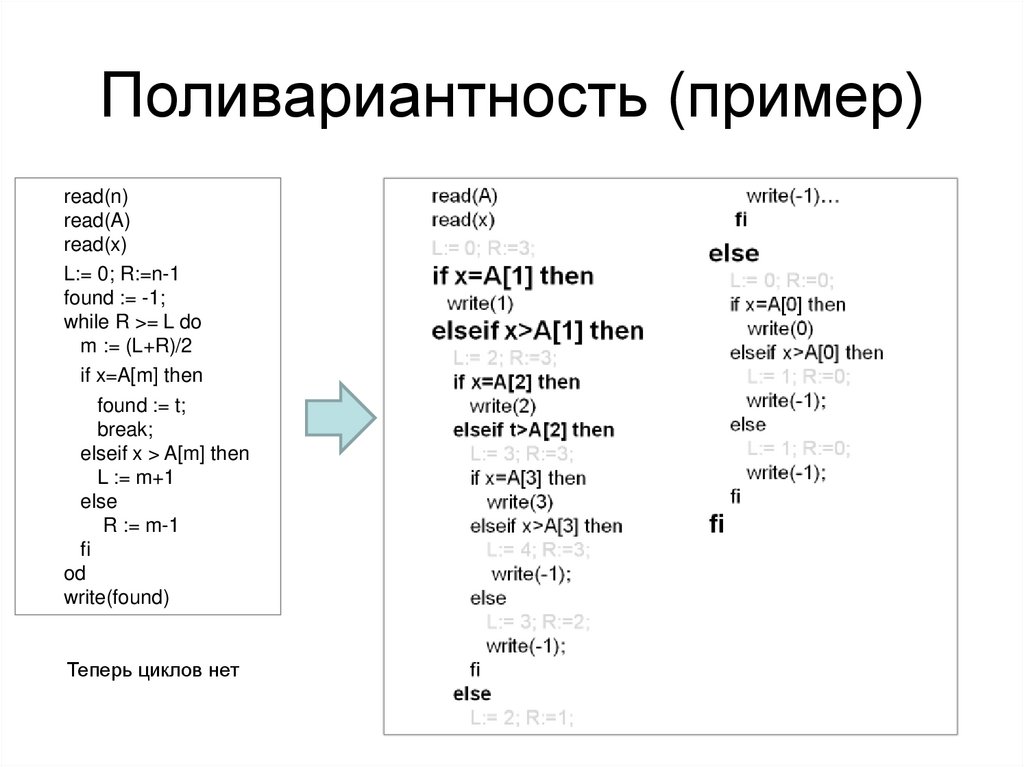
Поливариантность (пример)read(n)
read(A)
read(x)
L:= 0; R:=n-1
found := -1;
while R >= L do
m := (L+R)/2
if x=A[m] then
found := x;
break;
elseif x > A[m] then
L := m+1
else
R := m-1
fi
od
write(found)
read(n)
read(A)
read(x)
L:= 0; R:=n-1
found := -1;
if R >= L then
m := (L+R)/2
if x=A[m] then
found := x;
break;
elseif x > A[m] then
L := m+1
else
R := m-1
fi
while R >= L do … od
fi
write(found)
L и R зав от n но условие R>=L задержено
Раскручиваем
цикл
read(n)
read(A)
read(x)
L:= 0; R:=n-1
found := -1;
if R >= L then
m := (L+R)/2
if x=A[m] then
found := x;
break;
elseif x > A[m] then
L := m+1
while R >= L do … od
else
R := m-1
while R >= L do … od
fi
fi
write(found)
39.
Поливариантность (пример)read(n)
read(A)
read(x)
L:= 0; R:=n-1
found := -1;
while R >= L do
m := (L+R)/2
if x=A[m] then
found := t;
break;
elseif x > A[m] then
L := m+1
else
R := m-1
fi
od
write(found)
Теперь циклов нет
40.
Интерпретатор конечныхавтоматов
Представление конечного автомата
A=({a,b}, Q, q0, QF, )
• Q = 1..n
• q0 = 1
• (q,x) = nextx(q), x {a,b}
• q QF = accept(q)
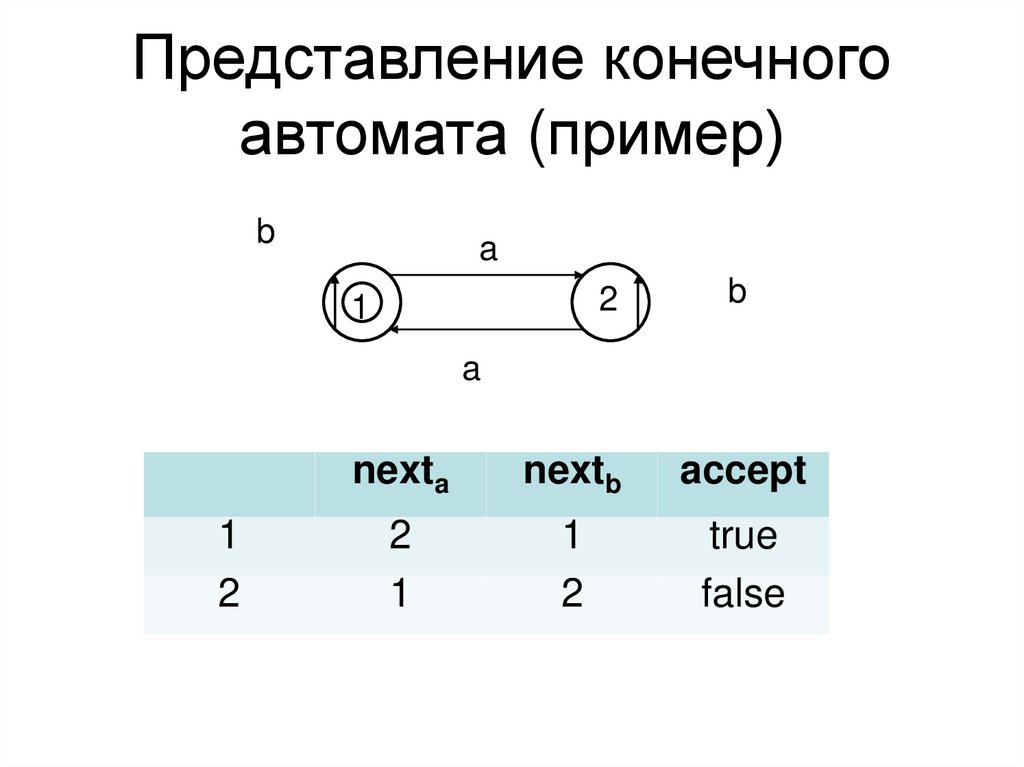
41.
Представление конечногоавтомата (пример)
b
a
2
1
b
a
1
2
nexta
nextb
accept
2
1
1
2
true
false
42.
Интерпретатор конечныхавтоматов
Int
Выч над q доступны, так как nexta,
nextb, accept доступны
read(nexta)
read(nextb)
read(accept)
q := 1
read(c)
while c != ‘#’ do
if c=‘a’ then
q := nexta[q]
else
q := nextb[q]
fi;
read(c)
od;
write(accept[q])
A=
nexta
nextb
accept
1
2
1
true
2
1
2
false
IntA = [mix] (Int, A) –
объектный код автомата
А в языке, в котором
записан интерпретатор
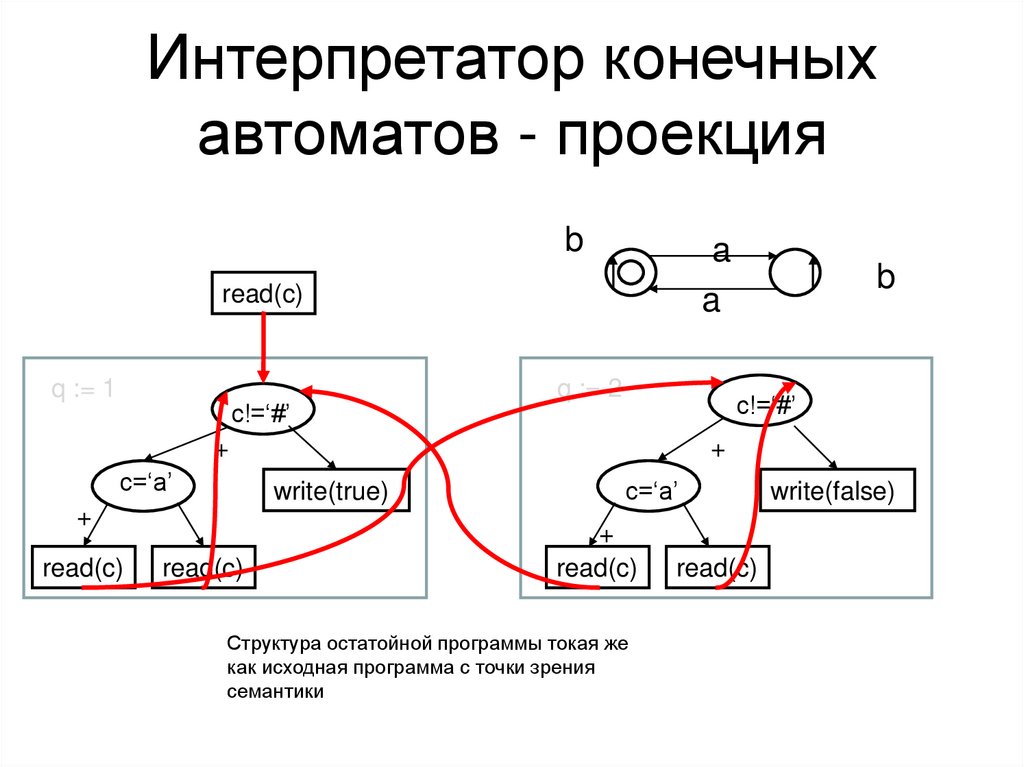
43.
Интерпретатор конечныхавтоматов - проекция
IntA
44.
Интерпретатор конечныхавтоматов - проекция
Есть зачикливание
(бесконеч дерево),
но есть шаблоны и
можно завернуть
проход обратно
read(c)
c!=‘#’
q := 1
c=‘a’
+
write(true)
+
read(c)
q := 2
read(c)
q := 1
c!=‘#’
c!=‘#’
+
c=‘a’
+
read(c)
q := 1
+
c=‘a’
write(false)
write(true)
+
read(c)
q := 2
read(c)
q := 2
read(c)
q := 1
45.
Интерпретатор конечныхавтоматов - проекция
b
a
a
read(c)
q := 1
c!=‘#’
q := 2
c!=‘#’
+
c=‘a’
read(c)
+
write(true)
+
read(c)
b
c=‘a’
+
read(c)
Структура остатойной программы токая же
как исходная программа с точки зрения
семантики
read(c)
write(false)
46.
Интерпретатор конечныхавтоматов - проекция
IntA
L1: read(c)
if c != ‘#’ then
if c=‘a’ then
L2: read(c)
if c != ‘#’ then
if c=‘a’ then
goto L1
else
goto L2
fi
else
write(false)
fi
else
goto L1
fi
else
write(true)
fi
47.
Входной языкпрограмма ::= { метка : оператор }+
оператор ::=
read переменная goto метка
| write выражение goto метка
| переменная := выражение goto метка
| goto метка
| if выражение then метка else метка
| stop
48.
Синтаксические категории• Var = {v} – переменные
• Expr = {e} – выражения
• Lab = {l} – метки
• Stmt = {stmt} - операторы
49.
{кол-во а – чётно}reada
readb
readc
inits
loop
check
select
a
b
out
end
: read(nexta) goto readb
: read(nextb) goto readc
: read(accept) goto inits
: q := 1 goto loop
: read(c) goto check
: if c=‘#’ then out else select
: if c=‘a’ then a else b
: q := nexta[q] goto loop
: q := nextb[q] goto loop
: write(accept[q]) goto end
: stop
50.
Семантические категории• Val – множество значений
• State = Var Val – состояние памяти,
State = { }
• Обозначение =[x1 v1, x2 v2,…,xn vn]
• Вычисление выражения
eval : Expr x State = Val
• Эффект присваивания
[x:=e] : State State
[x:=e]( ) [x eval(e, )]
51.
Редукция выражений• SVar Var – доступные переменные
• SState = SVar Val – состояние памяти
• red : Expr x SState Expr
• Примеры: SVar = {x,y}
– red(“x+z”, [x 1]) = “1+z”
– red(“x+y”, [x 1]) = “1+?”
– red(“x+y”, [x 1, y 2]) = “3”
– eval(“x+y”, [x 1, y 2]) = 3
52.
Редукция операторов• red : Stmt x SState Stmt
• Примеры: SVar = {x,y}
– red(“x := x+z”, [x 1]) = “x := 1+z”
– red(“x := x+y”, [x 1]) = “x := 1+?”
– red(“x := x+y”, [x 1, y 2]) = “”
53.
{кол-во а – чётно}Lab \ SState
?
1
2
loop
read(c)
read(c)
check
c=‘#’
c=‘#’
select
c=‘a’
c=‘a’
out
write(true)
write(false)
end
stop
stop
inits
a
b
54.
Конфигурация смешанноговычислителя
• A Lab x SState – множество активных
точек
• P Lab x SState – множество
пройденных точек
• Lab x SState Lab
55.
A:={(start,[])}, P:=Cмешанный
while A!= do
вычислитель
let cnf=(l, ) A
A := A \ {cnf}
if cnf P then
P := P U {cnf}
write(cnf+”:”)
let stmt = оператор, помеченный l
write(red(stmt, ))
A := A U step(stmt, )
fi
od
56.
red & stepred(stmt, )
read(x) goto l’
step(stmt, )
S
goto (l’, [x v]), где v – доступный {(l’, [x v])}
вход
D
read(x) goto (l’, )
{(l’, )}
write(e) goto l’
S,
D
write(red(e, )) goto (l’, )
{(l’, )}
x:=e goto l’
S
goto (l’, [x eval(e, ])
{(l’, [x eval(e, ])}
D
x := red(e, ) goto (l’, )
{(l’, )}
goto (if eval(e, ) then l’ else l’’ fi, )
{(if eval(e, ) then l’ else l’’
fi, }
D
if red(e, ) then (l’, ) else (l’’, )
{(l’, ), {(l’’, )}}
S,
D
stop
if e then l’ else S
l’’
stop
57.
Как сделать stmt доступным?let cnf=(l, ) A
...
let stmt =
оператор,
помеченный l
…
Менее эфективный
код, но ботее
доступные условия
let cnf=(l?, ) A
...
foreach l in Lab
if l = l? then
let stmt =
оператор,
помеченный l
...
58.
Трансляторконечных
автоматов
A:={(start,[])}, P:=
while A!= do
let cnf=(l, ) A
A := A \ {cnf}
if cnf P then
P := P U {cnf}
write(cnf+”:”)
case l of
“reada” : read(v); write(“goto (“readb”, [“nexta” v])”);
A := A U {(“readb”, [nexta v])}
“readb” : read(v); write(“goto (“readc”, [“nexta” v])”);
A := A U {(“readc”, [nexta v])}
“readс” : read(v); write(“goto (“inits”, [“accept” v])”);
A := A U {(“inits”, [“accept” v])}
“inits” : read(v); write(“goto (“loop”, [“q” v])”);
A := A U {(“loop”, [“q” v])}
…
59.
“loop” : write(“read(c) goto (“check”, )”);A := A U {(“check”, )}
“check” : write(“if red(“c=‘#’”, ) then (“out”, ) else (“select”, )”)
A := A U {(“out”, ), (“select”, )}
“select” : write(“if red(“c=‘a’”, ) then (“a”, ) else (“b”, )”)
A := A U {(“a”, ), (“b”, )}
“a” : write(“goto (“loop”, [“q” eval(“nexta[q]”, )])”)
A := A U {(“loop”, [“q” eval(“nexta[q]”, )])}
“b” : write(“goto (“loop”, [“q” eval(“nextb[q]”, )])”)
A := A U {(“loop”, [“q” eval(“nextb[q]”, )])}
“out” : write(“write(red(“accept[q]”, )”) goto (“stop”, )”)
A := A U {(“stop”, )}
“stop” : write(“stop”)
esac
fi
od
Транслятор
конечных
автоматов
60.
Оптимизации• Разбиение «составных» данных на
части
• Детерминизация выбора
• Редукция редукции
– red(“c=‘#’”, ) = “c=‘#’”
– red(“accept[q]”, ) = “eval(accept[q], )”
– eval(“1”, ) = 1
61.
read(nexta); write(“(“reada”,?) : goto (“readb”, )”)read(nextb); write(“(“readb”,?) : goto (“readc”, )”)
read(accept); write(“(“readc”,?) : goto (“inits”, )”)
write(“(“inits”,?) : goto (“loop”,1)”)
A:={(start,[])}, P:=
while A!= do
let cnf=(l,q) A; A := A \ {cnf}
if cnf P then
P := P U {cnf}
write(cnf+”:”)
write(“read(c) goto (“check”,q)”);
write(“(“check”,q) : if c=‘#’ then (“out”,q) else (“select”,q)”)
write(“(“select”,q) : if c=‘a’ then (“a”,q) else (“b”.q)”)
write(“(“b”.q) : goto (“loop”, nextb[q])”)
write(“(“a”,q) : goto (“loop”, nexta[q])”);
write(“(“out”,q) : write(accept[q]) goto (“stop”,q)”)
write(“(“stop”,q) : stop”)
A := A U {(“loop”, nextb[q]), (“loop”, nexta[q])}
fi
od
Транслятор
конечных автоматов
(оптимизированный)
62.
Анализ периода связывания• Binding Time Analysis = BTA
• Семантическа область
BTVal = {S,D}, D<S
• Состояние (доступности) памяти:
BTState = Var BTVal
• Частичный порядок b1<b2
x Var b1(x) < b2(x)
63.
BTA - cемантические функции• Вычисление выражения:
: Expr (BTState BTVal)
• Пример
even(n)[n S] = S
y*x [x D, y S] = D
64.
BTA - cемантические функции• Исполнение оператора:
: Stmt (BTState BTState)
• Пример
y:=1 [] = [y S]
y:=y*x [x D, y S] = [x D, y D]
65.
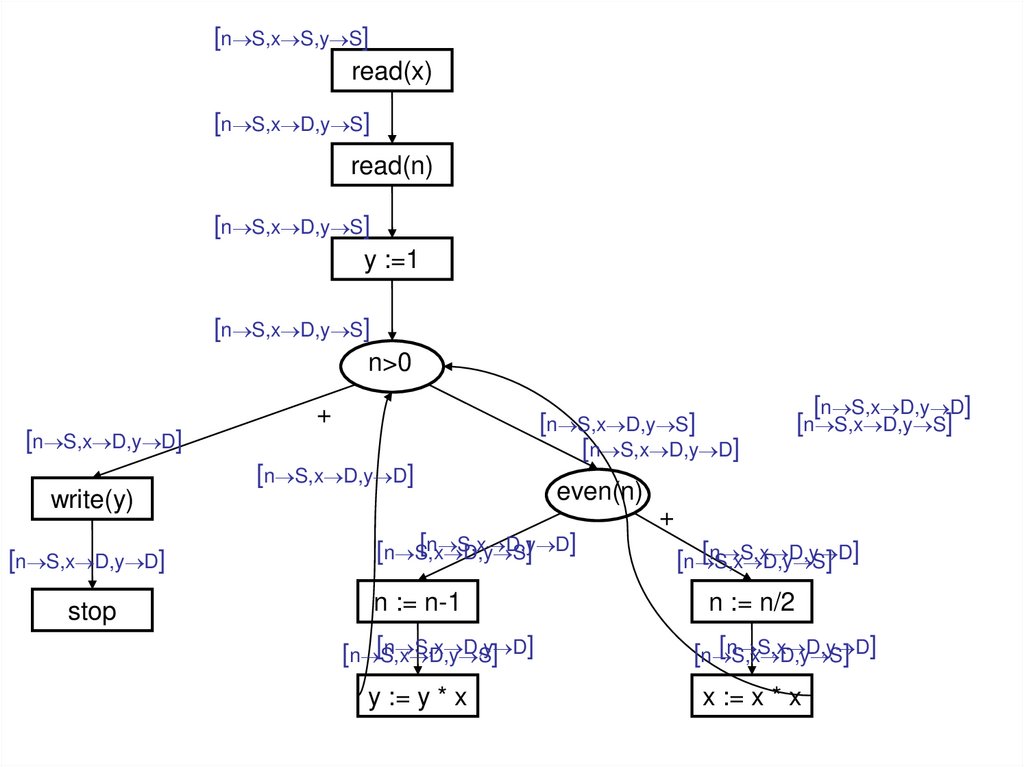
[n S,x S,y S]read(x)
[n S,x D,y S]
read(n)
[n S,x D,y S]
y :=1
[n S,x D,y S]
n>0
+
[n S,x D,y S]
[n S,x D,y D]
[n S,x D,y D]
[n S,x D,y D]
write(y)
[n S,x D,y D]
stop
[n S,x D,y D]
[n S,x D,y S]
even(n)
+
[n S,x D,y D
[n S,x D,y S
] ]
n := n-1
[n S,x D,y D
[n S,x D,y S
] ]
y := y * x
[n S,x D,y D
[n S,x D,y S
] ]
n := n/2
[n S,x D,y D
[n S,x D,y S
] ]
x := x * x
66.
BTA – как денотационнаясемантика
с = S
x = (x)
e1+e2 = e1 e2
even(e) = e
x:=e = [x e ]
s1;s2 = s2( s1
if e then s1 else s2 fi = s1 s2
while e do s od = fix ’. s ’
67.
Неподвижная точка• Оператор неподвижной точки:
(fix F) =F(fix F)
• Неподвижная точка для BTA
F BTOperator = BTState BTState
fix BTOperator BTState
68.
Примерwhile n>0 do if even(n)then n:=n/2;x:=x*x else n:=n-1;y:=y*x fi od =
= fix ’. if even(n)then n:=n/2;x:=x*x else n:=n-1;y:=y*x fi ’ =
= fix ’. n:=n/2;x:=x*x ’ n:=n-1;y:=y*x ’ =
= fix ’. x:=x*x ( n:=n/2 ’) y:=y*x ( n:=n-1 ’) =
= fix ’. x:=x*x ( ’[n n/2 ’]) y:=y*x ( n:=n-1 ’) =
= fix ’. x:=x*x ( ’[n n ’ 2 ’]) ... =
= fix ’. x:=x*x ( ’[n n ’ 22]) ... =
= fix ’. x:=x*x ( ’[n ’(n)]) ... =
= fix ’. ’ ... =
= fix ’. ’ ’[y ’(y) ’(x)]
69.
ПримерВычисление неподвижной точки (fix F), для
F = ’. [n S,x D,y S] ’ ’[y ’(y) ’(x)]
b0 = [n S,x S,y S]
b1 = F(b0) = [n S,x D,y S] [n S,x S,y S]
[n S,x S,y S][y
[n S,x S,y S](y) [n S,x S,y S](x)]
= [n S,x D,y S] [n S,x S,y S] [n S,x S,y S] =
= [n S,x D,y S]
b2 = F(b1) = [n S,x D,y S] [n S,x D,y S]
[n S,x D,y S][y
[n S,x D,y S](y) [n S,x D,y S](x)]
= [n S,x D,y S] [n S,x S,y S] [n S,x S,y D] =
= [n S,x D,y D]
b3 = F(b2) = [n S,x D,y D]
…
70.
BTA как система неравенств• Для всех присваиваний программы
x := e
и всех аргументов x’ выражения е
порождаем неравенство
bx bx’
• Для задержанных переменных x
порождаем равенство
bx = D
• Ищем максимальное решение
71.
ПримерНеравенство
Источник
bx = D
x - задержано
bn bn
n := n-1
by bx
y := y*x
by by
y := y*x
bn bn
n := n/2
bx bx
x := x*x
• bx = D bx
• by bx by
• bn bn
D
bx
by
bn
72.
Поливариантный BTA• Инструментируем исходную программу
вычислением задержанности
переменных
p(x,y) p’(x,dx,y,dy)
• Поливариантно специализируем p’
относительно заданных dx=S, dy=D:
p’SD(x,y) эквивалентна p(x,y)
• Специализируем p’SD при доступном x и
задержанном y.
73.
Пример – xninit:
read(x); read(n); y:=1 goto loop
loop:
if n>0 then body else out
body:
if even(n) then div else dec
div:
n := n/2; x := x*x;
goto loop
dec :
n := n-1; y := y*x;
goto loop
out :
write(y); stop
74.
xn – BT-инструментированныйinit:
read(x); read(dx);
read(n); read(dn);
y := 1; dy:=S;
goto loop
loop:
if n>0 then body else out
body:
if even(n) then div else dec
div:
n := n/2; x := x*x;
dn:=dn S; dx:=dx dx;
goto loop
dec :
n := n-1;y := y*x;
dn:=dn S; dy:=dy dx;
goto loop
out :
write(y); stop
75.
xn – BT-инструментированныйinitSSS:
read(x); read(n); yS := 1; goto loopDSS
initDSS:
loopSSS:
loopDSS:
if n>0 then body elseDSS outDSS
bodySSS:
bodyDSS:
if even(n) then divDSS else decDSS
divDSS:
n := n/2; x := x*x; goto loopDSS
decDSS:
n := n-1;yD := yS*x; goto loopDDS
outDSS:
write(y); stop
divSSS:
decSSS :
outSSS :
• Формат метки:
{label}{dx}{dy}{dn}
• yS и yD – разные
компоненты связности
информационного
графа
initDDS:
loopDDS:
if n>0 then body elseDDS outDDS
bodyDDS:
if even(n) then divDDS else decDDS
divDDS:
n := n/2; x := x*x; goto loopDDS
decDDS:
n := n-1;yD := yD*x; goto loopDDS
outDDS:
write(y); stop
76.
Пример – xninitSSS.?.?:
read(x); goto loopDSS.3.1
loopDSS.3.1:
yD := 1*x; goto loopDDS.2.1
loopDDS.2.1:
x := x*x; goto loopDDS.1.1
loopDDS.1.1:
yD := yD*x; goto loopDDS.0.1
loopDDS.0.1:
write(y); stop
• Формат метки: {label}{dx}{dy}{dn}.{n}.{yS}
77.
Пример - evalproc eval(e : Expr, s : Stat) : Value
case e of
“c” : return c.value;
“x” : return s[“x”];
“e1+e2” : return eval(e1,s) + eval(e2,s);
esac;
78.
Пример - evalproc eval(2*3+4)*x(s : Stat) : Value
return eval2*3+4(s) * evalx(s);
proc eval2*3+4(s : Stat) : Value
return eval2*3 (s) + eval4(s);
proc eval2*3(s : Stat) : Value
return eval2(s) * eval3(s);
proc eval2(s : Stat) : Value
return 2;
proc eval3(s : Stat) : Value
return 3;
proc eval4(s : Stat) : Value
return 4;
proc evalx(s : Stat) : Value
return s[“x”];
proc eval(2*3+4)*x(s : Stat) : Value
return (2*3+4) * s[“x”];
79.
Пример - evalproc eval(e : Expr, s : Stat) : Value
proc isStatic(e : Expr) : bool
if isStatic(e) then
case e of
return evalStatic(e)
“c” : return true;
else
“x” : return false;
case e of
“e1+e2” :
“c” : return c.value;
return isStatic(e1)
“x” : return s[“x”];
and isStatic(e2);
“e1+e2” : return eval(e1,s) + eval(e2,s);
esac
esac;
fi
proc evalStatic(e : Expr) : Value
case e of
“c” : return c.value;
“e1+e2” :
return evalStatic(e1) +
evalStatic(e2);
esac
80.
Пример - evalproc eval(2*3+4)*x(s : Stat) : Value
return eval2*3+4(s) * evalx(s);
proc eval2*3+4(s : Stat) : Value
return 10;
proc evalx(s : Stat) : Value
return s[“x”];
proc eval(2*3+4)*x(s : Stat) : Value
return 10*s[“x”];







































































 programming
programming








