Развитие творческих способностей учащихся на уроках математики

1.

Развитие творческих
способностей учащихся на
уроках математики
Учитель математики
ИГОЛ им.Е.Г.Лукьянец
Ширшова Н.В
17.02.2017.

2.

Что же такое творческие способности?
Творческие способности – это
способности человека, которые
порождают
нечто
качественно
новое, никогда раньше не бывшее,
не существовавшее.

3.

Любой ли человек обладает способностями
к математике?
Способность
к
восприятию
математики
распространена
в
человечестве, пожалуй, даже в
большей степени, чем способность
получать
удовольствие
от
приятной мелодии – она присуща
огромному большинству. (Г.Харди)

4.

Типы задач для развития активного
самостоятельного, творческого мышления
• Задачи с не сформулированным
вопросом.
• Задачи с недостающими или
излишними данными.
• Задачи с несколькими решениями.
• Задачи с меняющимся
содержанием.
• Задачи на логическое мышление.

5. На рисунке изображена трапеция ABCD.

На рисунке
ABCD.
изображена
трапеция
Найти:
1. Площадь трапеции
2. sinA, cosA, tgA, sinABH и т.п.
3. Стороны.
4. Среднюю линию трапеции.
5. Расстояние от точки С до
прямой AD.
6. Расстояние от вершины А до
стороны CD.
7. Площади треугольников ABD и
ACD.
8. Длину диагонали BD.
9. Радиус окружности, описанной
около треугольника ABD.
10. Можно ли в данную трапецию
вписать окружность?

6. Что остается за кадром?

• Может быть сформулирована задача,
для решения которой недостаточно
данных.
• Данных достаточно, но недостаточно
знаний
учащихся
(не
пройден
материал).

7. Формулировки исследовательских (творческих) заданий

• «Исследовать …»
• «Верно ли, что если …, то…?»
• «Определить, какое из выражений больше:
13
14
14
?»
13 или
• «Найти условие, при котором…»
• «Существуют ли такие значения с, при
которых…?»

8. Процесс решения задачи – случайный процесс?

9. Схема

Дано: условие, известно
Р………………………..
Е………………………..
Ш………………………
Е………………………..
Н……………………….
И……………………….
Е……………………….
Надо: найти, доказать
Цепочка тезисов,
которые соединяют
«дано» и то, что
«надо»
Что для этого нужно?

10. Естественность?

• Верно ли, что среди любых
11 натуральных чисел можно
найти 2, разность которых
будет делиться на 10?

11. Решение?

• Так как дано 11 целых чисел, то по принципу
Дирихле есть хотя бы 2 числа а и в, которые имеют
одинаковые остатки r при делении на 10.
• a=10m+r
• b=10n+r
• a-b=(10m+r) – (10n+r) = 10m+r – 10n – r=10(m-n)
• Если в произведении хотя бы один из множителей
делится на 10, то и все произведение делится на 10.

12. Какой вопрос возникает по прочтению задачи?

• Что нужно, чтобы разность чисел
делилась на 10?
• На конце у разности должен быть 0.
• В каком случае это будет?

13. Численный эксперимент:

16 – 8;
23 – 10;
28 – 12;
25 – 5
• Последние цифры должны быть одинаковые.
• Почему среди 11 чисел найдется 2
числа, у которых последние цифры
одинаковые?

14. Что остается за кадром?

Знания фактов, знание теорем
Есть тупиковые ветви
Творчество?

15. Задача

На рынке некий покупатель, желая приобрести
шапку за 10 рублей, дал продавцу купюру
достоинством 25 рублей. У продавца сдачи не
было, поэтому он сбегал к своему другу,
торговцу, чтобы разменять деньги. После чего
отдал покупателю шапку и 15 рублей сдачи. Через
некоторое время пришел его друг со словами:
«Купюра фальшивая, забирай ее себе, а мне
верни деньги». Продавец был человеком
честным, и отдал другу 25 рублей. Сколько в
итоге
потерял
продавец
в
денежном
эквиваленте?

16. Решение:

Экономист (бухгалтер):
Приход + 25 (от друга)
Расход – 25 (шапка + сдача) - 25 (отдал другу)
Итого: -25 у продавца
Физик: энергия в замкнутой системе сохраняется:
Друг: 0
Покупатель: +25
Значит, продавец: - 25.
Математик: предположим, что купюра настоящая.
Тогда все операции честные и никто ничего не
потерял. А теперь вспомним, что бумажка 25
рублей – фальшивая, которая осталась на руках у
продавца. Значит, продавец теряет 25 рублей.

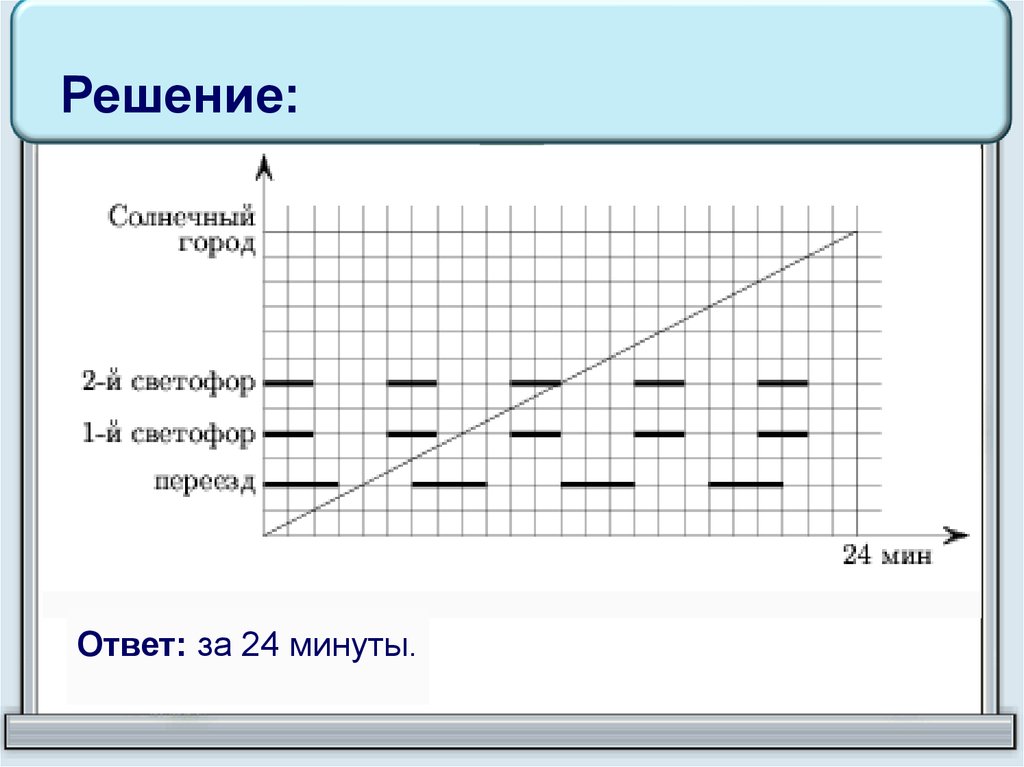
17. Задача

Из Цветочного города в Солнечный ведёт
шоссе длиной 12 км. На втором километре этого
шоссе расположен железнодорожный переезд,
который три минуты закрыт и три минуты открыт и
т.д., а на четвёртом и на шестом километрах
расположены светофоры, которые две минуты горят
красным светом и три минуты – зелёным и т.д.
Незнайка выезжает из Цветочного города в
Солнечный в тот момент, когда переезд только что
закрылся,
а
оба
светофора
только
что
переключились на красный. За какое наименьшее
время (в минутах) он сможет доехать до Солнечного
города, не нарушая правил, если его электромобиль
едет по шоссе с постоянной скоростью (Незнайка не
умеет ни тормозить, ни увеличивать скорость)?

18. Решение:

Ответ: за 24 минуты.

19.

Если ученик в школе не научился
сам ничего творить, то и в жизни он
всегда будет только подражать,
копировать, так как мало таких,
которые
бы,
научившись
копировать,
умели
сделать
самостоятельное приложение этих
сведений.
(Л.Толстой)