Применение векторов к решению задач. Геометрия. 9 класс

1.

Применение векторов
к решению задач
Геометрия 9 класс

2.

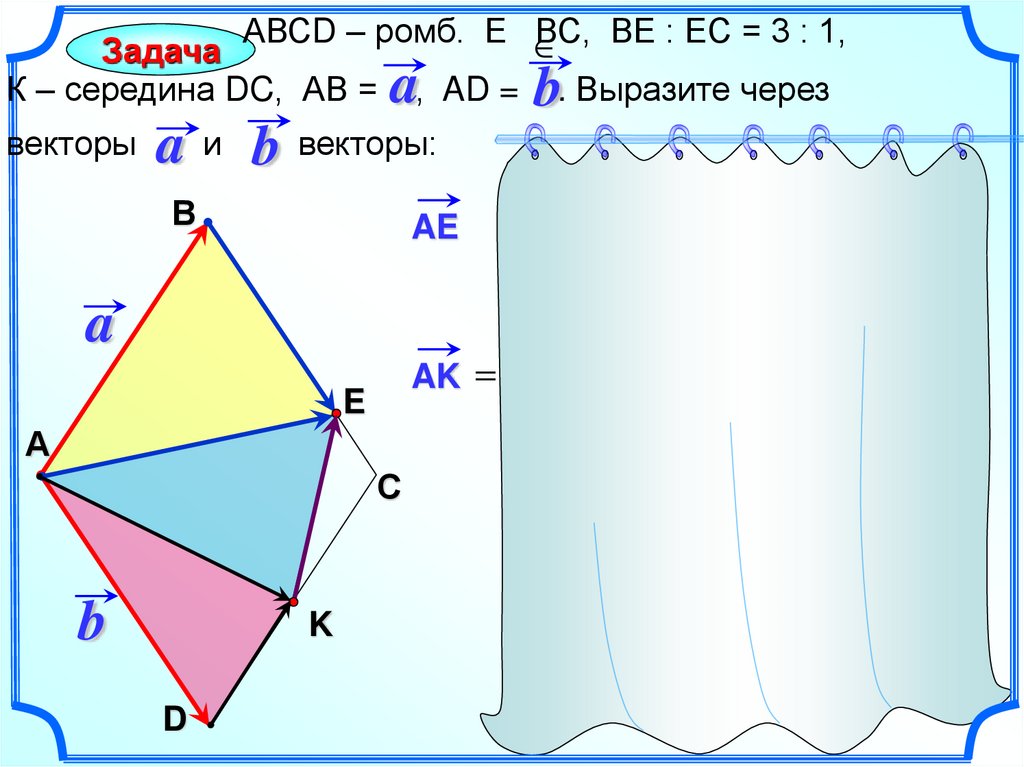
АВСD – ромб. Е
ВС, ВЕ : ЕС = 3 : 1,
Задача
К – середина DC, АВ =
векторы
a, AD = b. Выразите через
a и b векторы:
В
AE
a
1
AK AD DK AD DС
2
E
А
С
b
K
D
3
AB BE AB BC
4
1
b a
2

3.

На стороне ВС ромба АВСD лежит точка К так, что
ВК=КС, О- точка пересечения диагоналей.
Выразите векторы АО, АК, КD через векторы а= АВ
и b=АD
АО-половина
С Выразим АО,АО=½∙(а
+ b)
Значит АО=½ АС
диагонали АС
Вектор АС = а + b (по правилу пар-ма)
К
В
О
а
А
Выразим АК
По свойству ромба АD=ВС, АD//ВС
D
ВК=½ВС, ВК=½ b
АК=b=а ВС
+ ½, b
Выразим КD
b
Используем векторы b и АК
КD= b - (а + ½ b)= ½b - a

4.

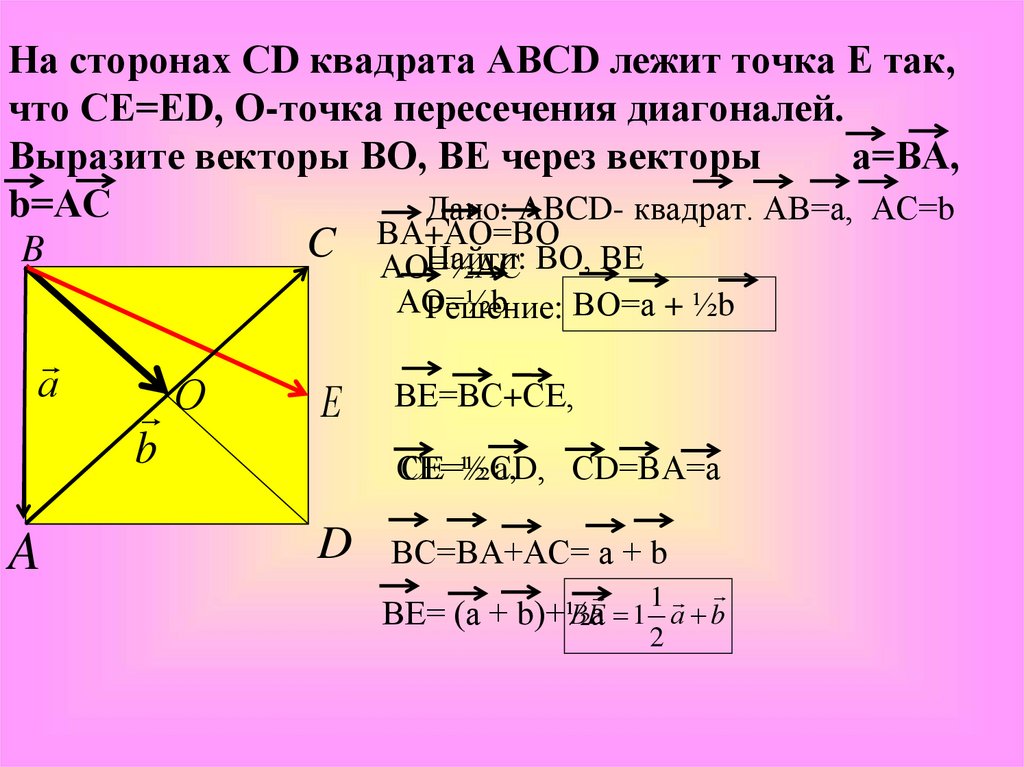
На сторонах СD квадрата АВСD лежит точка Е так,
что СЕ=ЕD, О-точка пересечения диагоналей.
Выразите векторы ВО, ВЕ через векторы
а=ВА,
b=АС
Дано: ABCD- квадрат. АВ=а, АС=b
C ВА+АО=ВО
B
Найти: ВО, ВЕ
АО=½АС
АО=½b
Решение: ВО=а + ½b
а
A
О
b
Е
ВЕ=ВС+СЕ,
СЕ=½
СЕ=½СD,
a,
СD=ВА=а
D
ВС=ВА+АС= а + b
1
ВЕ 1 а b
ВЕ= (а + b)+½а
2

5.

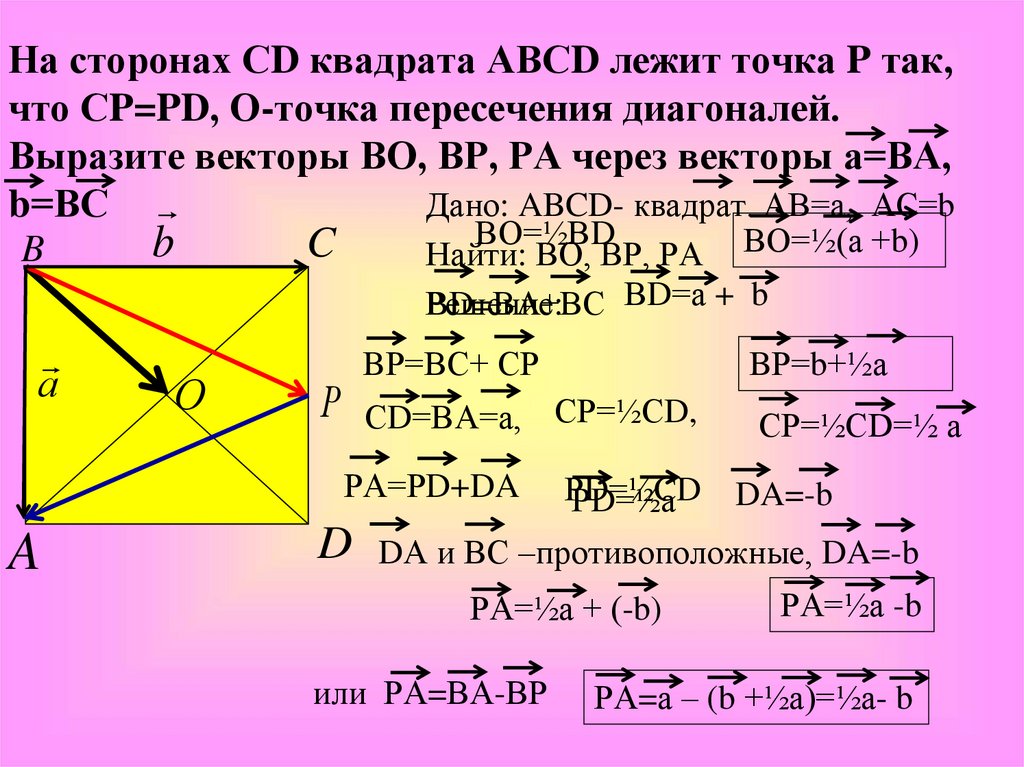
На сторонах СD квадрата АВСD лежит точка P так,
что СP=PD, О-точка пересечения диагоналей.
Выразите векторы ВО, ВР, РА через векторы а=ВА,
Дано: ABCD- квадрат. АВ=а, АС=b
b=ВС
ВО=½ВD
b
C
B
Найти: ВО, ВР, РА ВО=½(а +b)
ВD=ВА+ВС ВD=а + b
Решение:
а
A
О
BР=ВС+ СР
BР=b+½а
Р СD=ВА=а,
СР=½СD,
РА=РD+DA
РD=½CD
DA=-b
РD=½а
СР=½СD=½ a
D DА и ВС –противоположные, DA=-b
РА=½а + (-b)
или РА=ВА-ВР
РА=½а -b
РА=а – (b +½а)=½а- b

6.

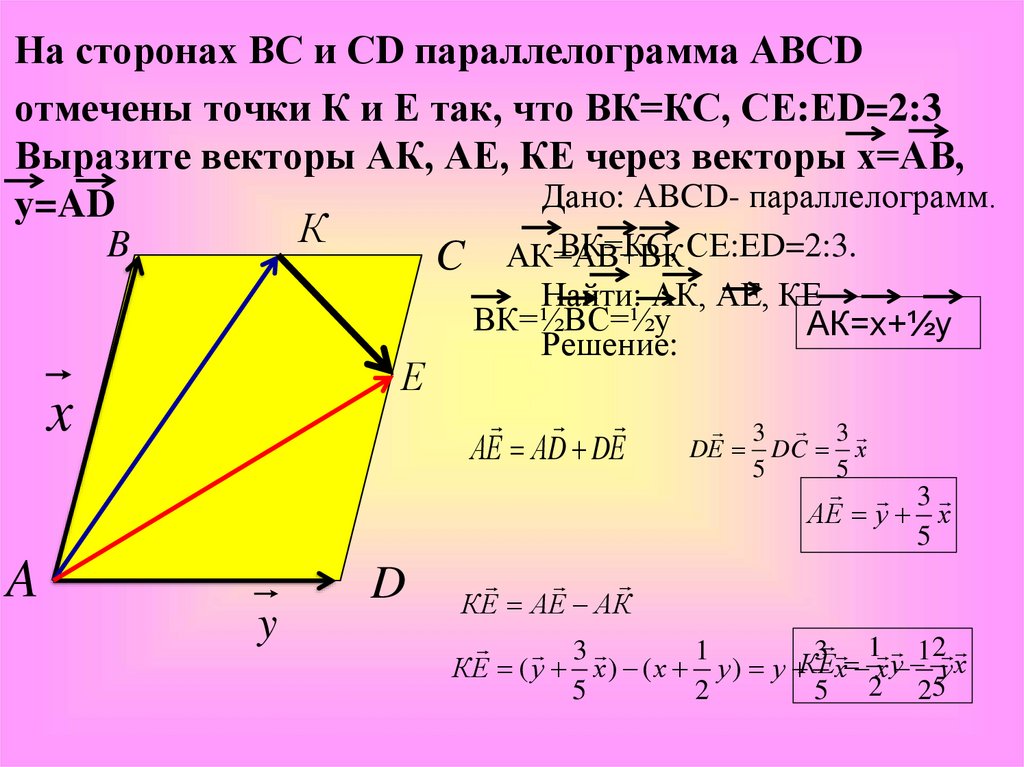
На сторонах ВС и СD параллелограмма АВСD
отмечены точки К и Е так, что ВК=КС, СЕ:ЕD=2:3
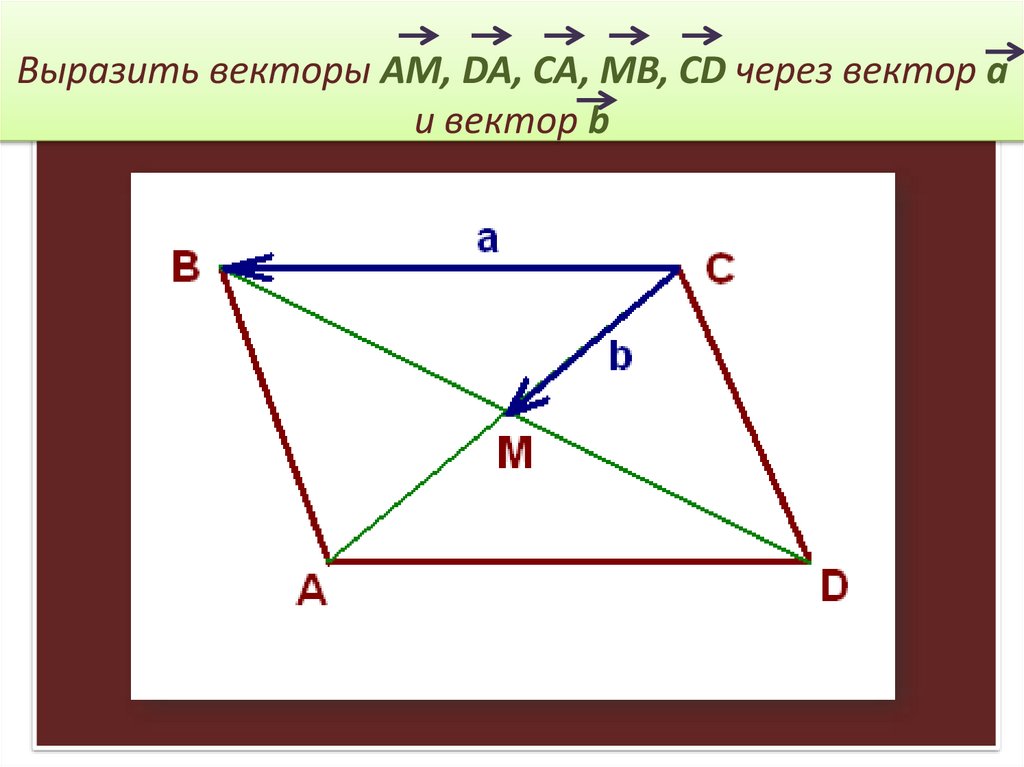
Выразите векторы АК, АЕ, КЕ через векторы х=АВ,
Дано: ABCD- параллелограмм.
у=AD
К
B
BК=КC, СЕ:ЕD=2:3.
C АК=АВ+ВК
Е
x
Найти: АК, АЕ, КЕ
ВК=½ВС=½у
АК=х+½у
Решение:
АЕ АD DЕ
3 3
DЕ DC х
5
5
3
АЕ у х
5
A
y
D
КЕ АЕ АК
3
1
3 1 12
КЕ ( у х ) ( х у ) у КЕх х у ух
5
2
5 2 25

7.

В равнобедренной трапеции высота делит большее
основание на отрезки, равные 6 и 12см. Найдите
среднюю линию трапеции. Дано: АВСD –трапеция, АD-
C большее основание СН-высота,
B
НD=6см, АН=12см
Решение:
Найти:
КL-средняя линия
К
A М
L
12
Н 6D
ВС АD
Трап.
равнобедренная,
<А=<D,
КL
2
<В=<С, АВ=СD
Чтобы найти ср. линию надо
АD= 6+12=18cм. Найдем ВС.
Проведем высоту ВМ
АМ=НD=6 т.к. ∆ВМА=∆СНD
ВС=МН- как отрезки прямых заключенных между параллельными
прямыми ВМ//CH (т.к. ВМ┴АD, СН┴АD) МН=ВС=6см
ΔВМА=ΔСНD равны по гипотенузе ВА=СD и острому углу <А=<D
6 18 24
Значит МН=12-6=6см
КL
12см
2
2
Ответ: 12см

8.

В равнобедренной трапеции один из углов равен 60º,
боковая сторона равна 10см, а меньшее основание 6
см. Найдите среднюю линию трапеции.
B
6
C
10
К
L
Дано: АВСD –трапеция,
<НDC=60º АВ=10см, ВС=6см.
Решение:
Найти:
КL-средняя линия
Трап. Равнобедренная,
<А=<D,
ВС АD
Чтобы
найти
ср.
линию
КL АВ=СD=10см надо
<В=<С,
2
ВС 6см АD ?
60
A М
Рассмотрим ∆ СНD-прямоугольный
НD=5
<D=60º
то <НCD=30º HD=½СD,
ВМ-высота
Н D Проведем
AD=АМ+МН+НD=5+6+5=16см.
ВС=МН=6см
заключенные
пар-миАМ=НD=5см
прямыми.
∆АМВ=∆DHCкак
по отрезки
гипотенузе
и острому между
углу. Значит
КL
АМ-?
6 16 22
11
2
2
Ответ :11см

9.

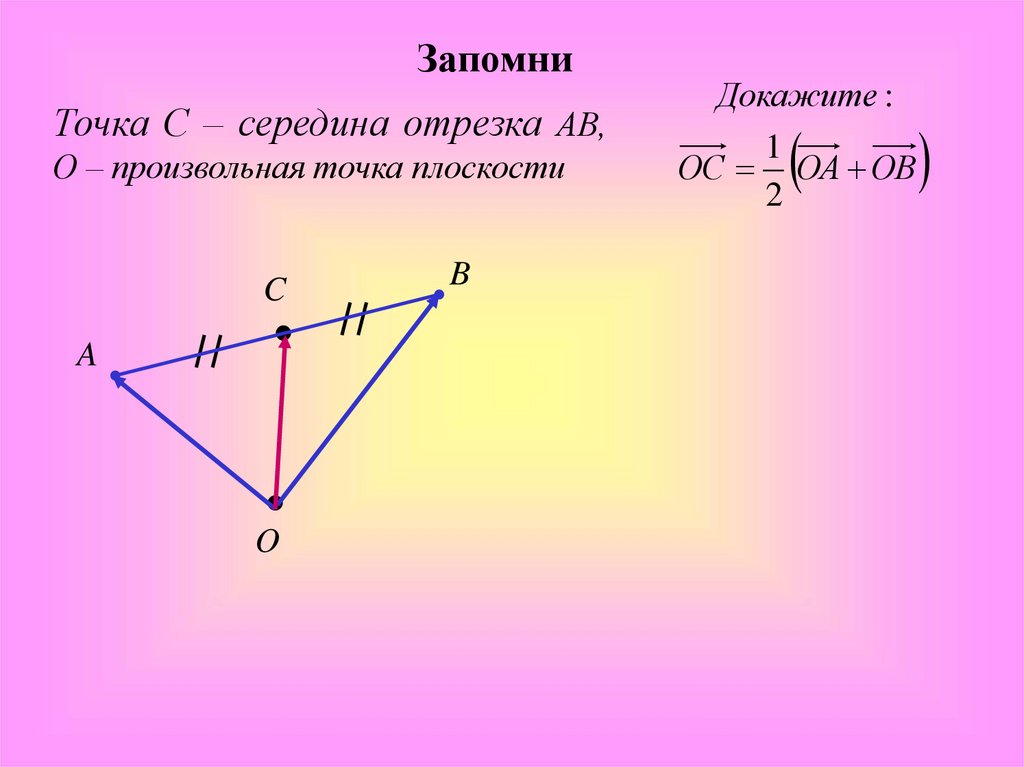
Запомни
Точка С – середина отрезка АВ,
О – произвольная точка плоскости
C
A
O
B
Докажите :
1
ОС ОА ОВ
2

10.

Прямая,
проведенная
через
середины
оснований трапеции проходит через точку
пересечения продолжений боковых сторон.
O
В
А
М
N
С
D

11.

В трапеции АВСD основания АD и
ВС относятся как 3 : 1, Е – середина
стороны АВ.
Докажите :
2
1
DE DA DC
3
2
B
E
х
DA 3СВ 3x
C
DA
x
3
у
ВА ...
y
DA DC
2
2
3
2
2
1
DE DA DC
3
2
DE 2 x
A
D
DE ...

12. Выразить векторы AM, DA, CA, MB, CD через вектор a и вектор b

13. Домашнее задание

14. № 1 Выразить векторы ВС, CD, AC, OC, OA через векторы а и b

15. № 2 Выразить векторы DP, DM, AC через векторы а и b

16. № 3 Дан параллелограмм ABCD. СР : PD = 2 : 3; AK : KD = 1 : 2. Выразить векторы СК, РК через векторы а и b

17. № 4 Дан прямоугольник ABCD. ВK : KС = 3 : 4. Выразить векторы АК, DК через векторы а и b