Алгоритм Прима (алгоритм поиска минимального остовного дерева)

1. Алгоритм Прима

(алгоритм поиска минимального
остовного дерева)

2. Алгоритм Прима

Шаг 1. Включить любую вершину в остов.
Шаг 2. Рассмотреть все ребра, исходящие
из вершин, включенных в остов к
оставшимся вершинам, и из них выбрать
ребро с минимальным весом. Его
концевую вершину включить в остов.
Повторять Шаг 2, пока все вершины не
будут включены в остов.

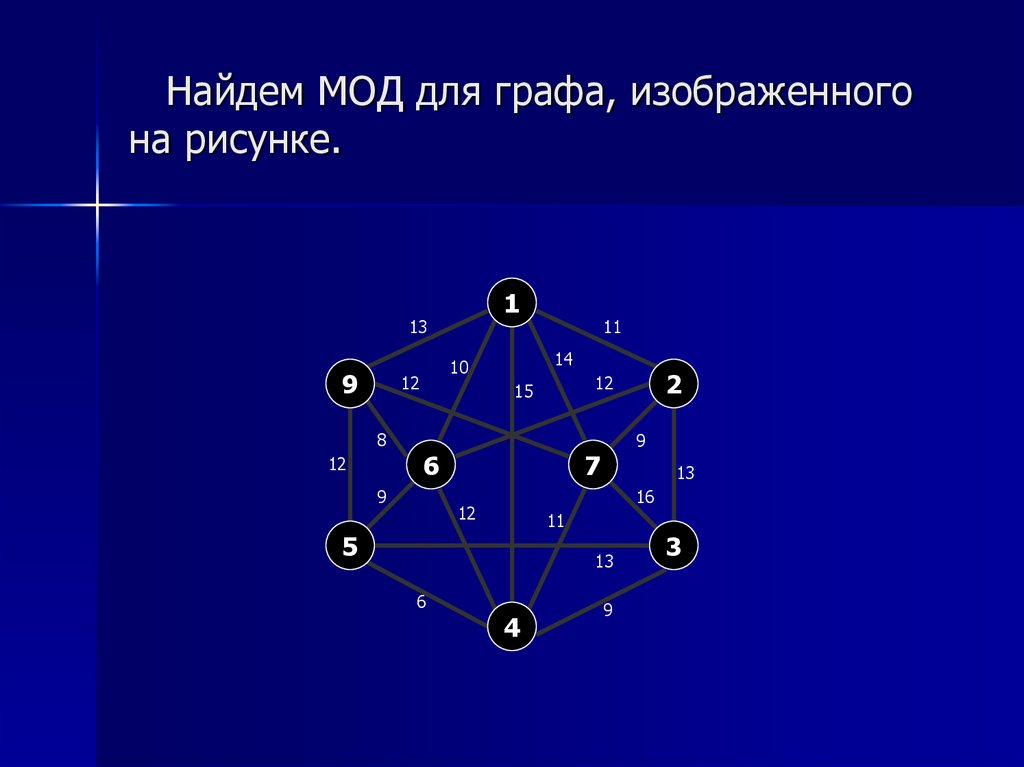
3. Найдем МОД для графа, изображенного на рисунке.

1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

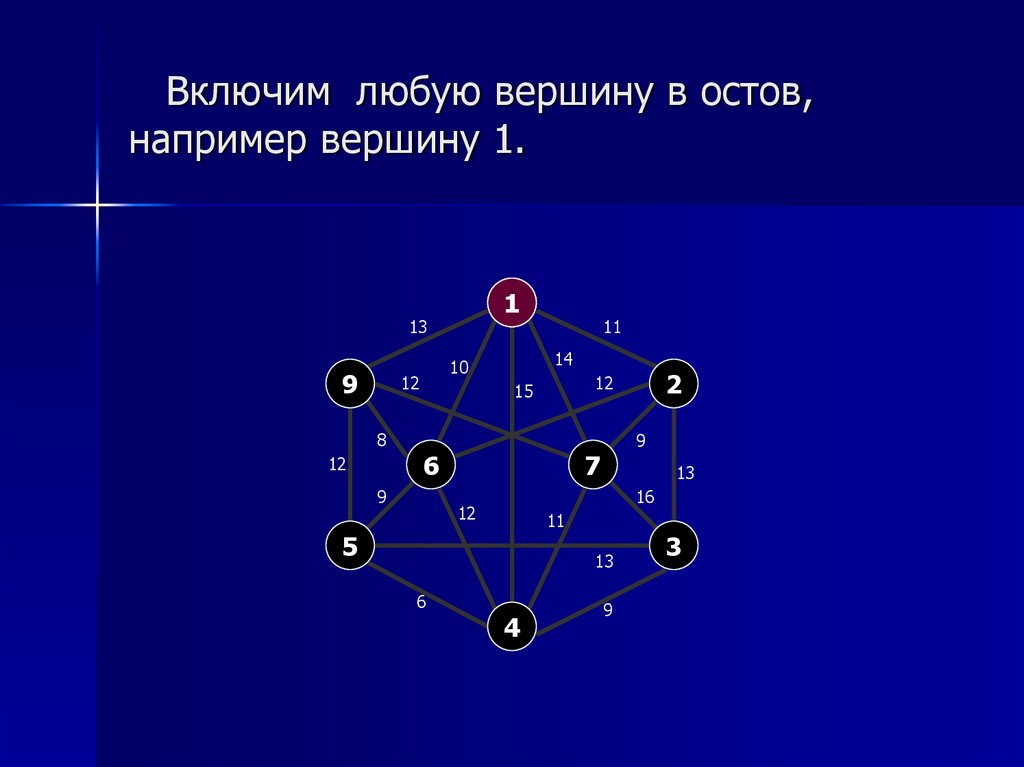
4. Включим любую вершину в остов, например вершину 1.

1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

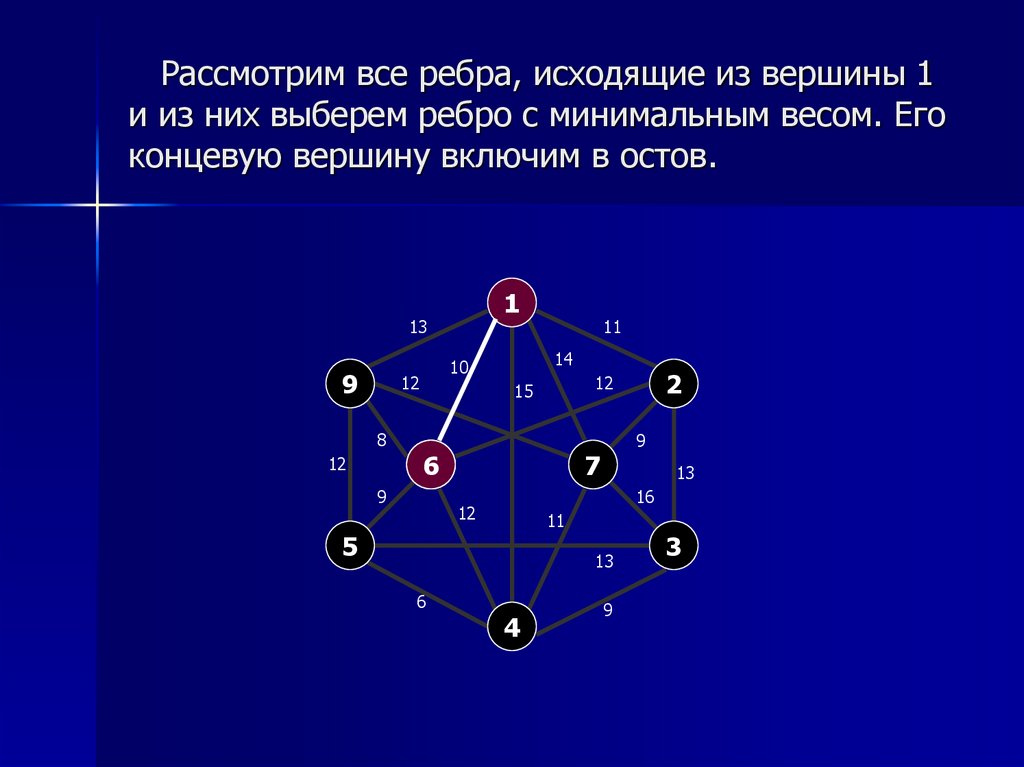
5. Рассмотрим все ребра, исходящие из вершины 1 и из них выберем ребро с минимальным весом. Его концевую вершину включим в остов.

1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

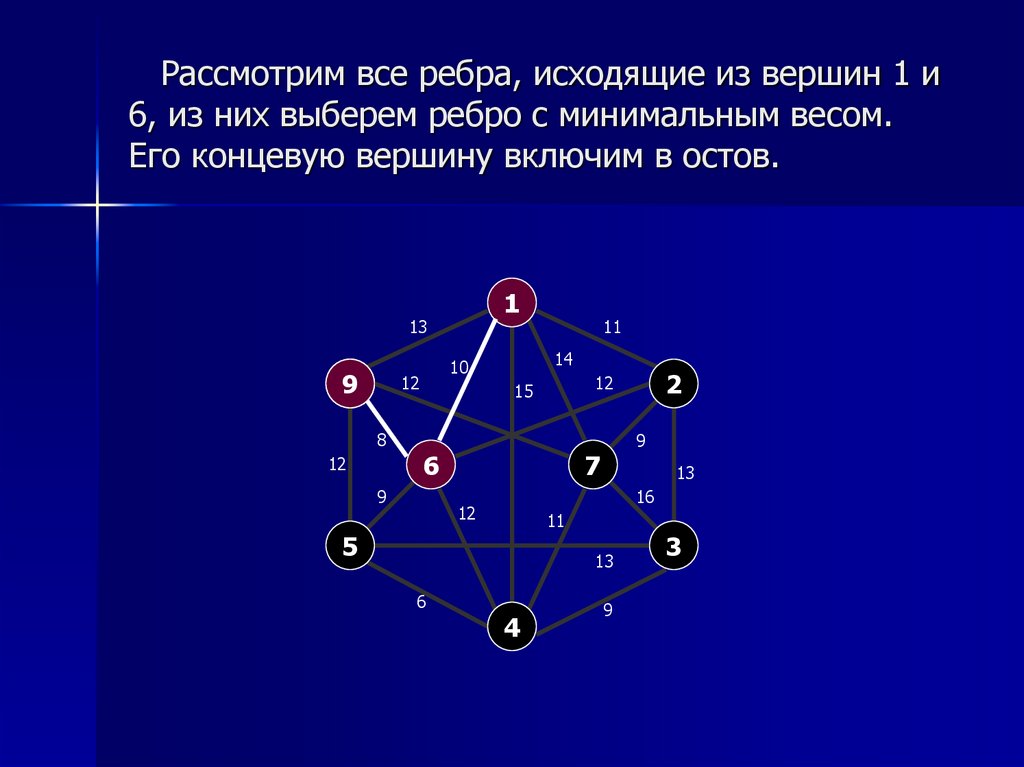
6. Рассмотрим все ребра, исходящие из вершин 1 и 6, из них выберем ребро с минимальным весом. Его концевую вершину включим в

остов.
1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

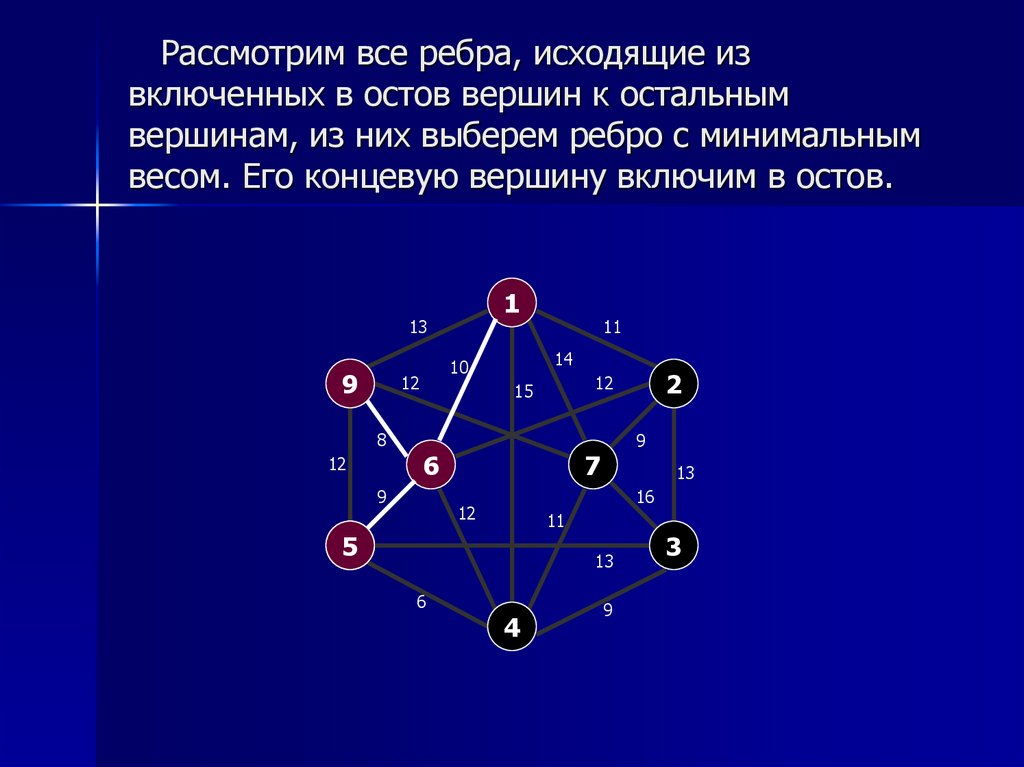
7. Рассмотрим все ребра, исходящие из включенных в остов вершин к остальным вершинам, из них выберем ребро с минимальным весом.

Его концевую вершину включим в остов.
1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

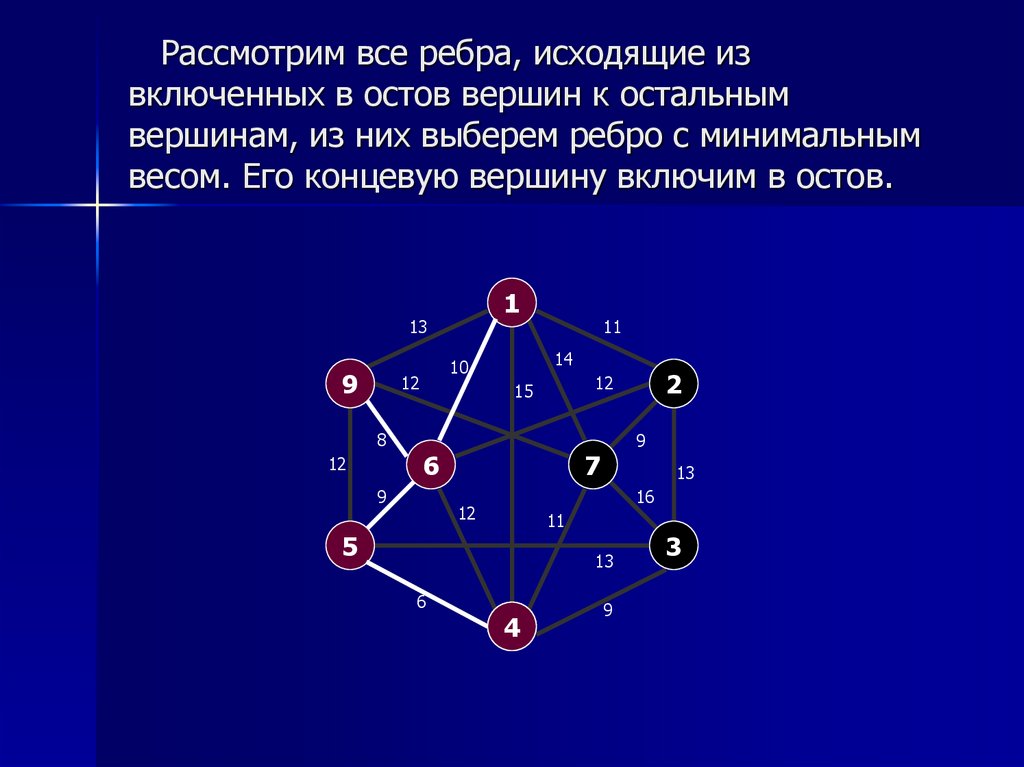
8. Рассмотрим все ребра, исходящие из включенных в остов вершин к остальным вершинам, из них выберем ребро с минимальным весом.

Его концевую вершину включим в остов.
1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

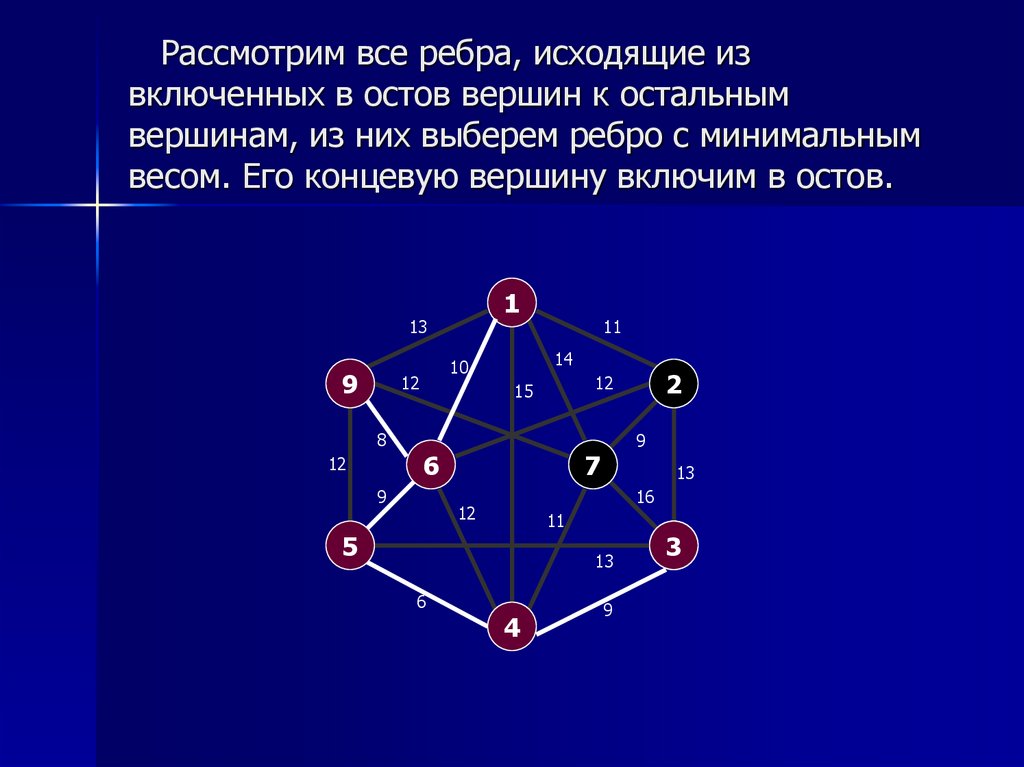
9. Рассмотрим все ребра, исходящие из включенных в остов вершин к остальным вершинам, из них выберем ребро с минимальным весом.

Его концевую вершину включим в остов.
1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

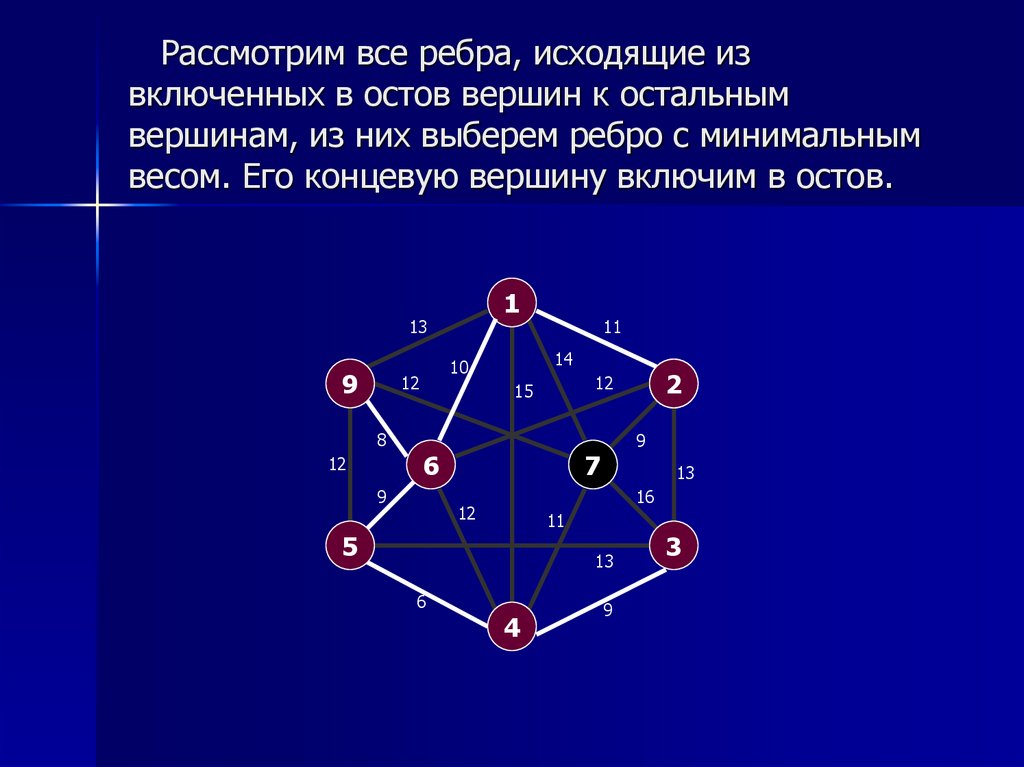
10. Рассмотрим все ребра, исходящие из включенных в остов вершин к остальным вершинам, из них выберем ребро с минимальным весом.

Его концевую вершину включим в остов.
1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

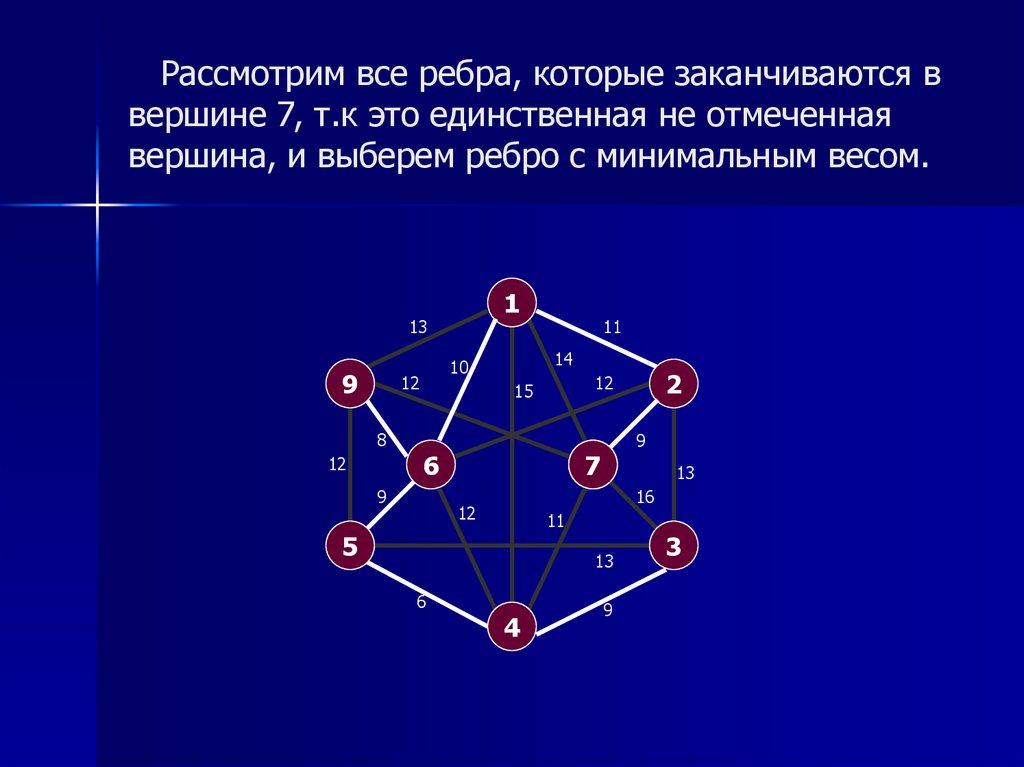
11. Рассмотрим все ребра, которые заканчиваются в вершине 7, т.к это единственная не отмеченная вершина, и выберем ребро с

минимальным весом.
1
13
9
8
12
14
10
12
11
6
9
9
7
13
16
12
11
5
13
6
2
12
15
4
9
3

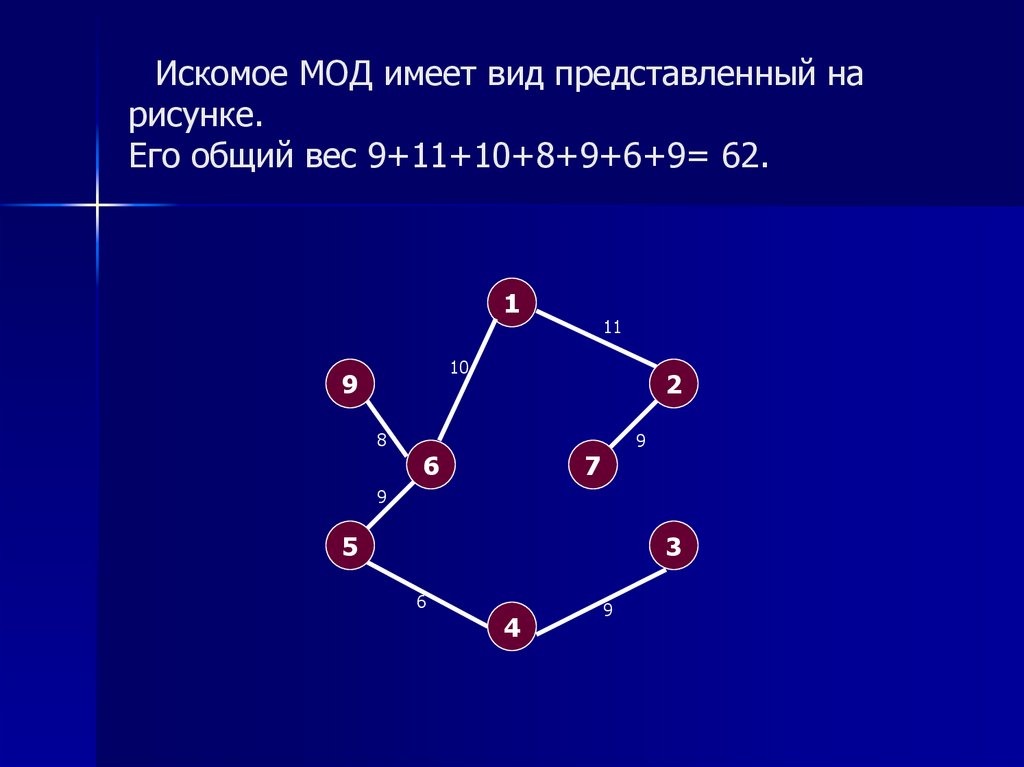
12. Искомое МОД имеет вид представленный на рисунке. Его общий вес 9+11+10+8+9+6+9= 62.

1
11
10
9
8
2
6
9
7
9
5
3
6
4
9

13. Замечания:

Пока не знаю!