Similar presentations:
Основы алгоритмизации. Алгоритм
1.
ОСНОВЫАЛГОРИТМИЗАЦИИ
2.
АЛГОРИТМАлгоритм – это метод (способ)
решения задачи, записанный по
определенным правилам,
обеспечивающим однозначность его
понимания и механического
исполнения при всех значениях
исходных данных (из некоторого
множества значений)
3.
СВОЙСТВА АЛГОРИТМОВДискретность алгоритма
• Процесс решения задачи, определяемый алгоритмом, разделен на отдельные элементарные
действия. Алгоритм представляет собой последовательность указаний, определяющих порядок
выполнения
Определенность алгоритма
• Каждая команда алгоритма должна быть понятна исполнителю, не оставлять место для ее
неоднозначного толкования и неопределенного исполнения
Результативность алгоритма
• Алгоритм всегда приводит к результату через конечное число шагов
Массовость алгоритма
• Каждый алгоритм должен быть применим для решения задач этого типа при всех допустимых
значениях переменных
4.
СПОСОБЫ ОПИСАНИЯ АЛГОРИТМОВСловесноформульное
описание
алгоритма
Графическое
описание
алгоритма
Описание
алгоритма на
алгоритмическо
м языке
5.
СЛОВЕСНО-ФОРМУЛЬНОЕ ОПИСАНИЕАЛГОРИТМОВ
Описание алгоритмов с помощью слов и формул
Пример 1
Составить алгоритм начисления зарплаты согласно следующему правилу:
Если стаж сотрудника менее 5 лет, то зарплата 130 тыс. руб., при стаже работы
от 5 до 15 лет – 180 тыс. руб. , при стаже свыше 15 лет зарплата с каждым
годом повышается на 10 тыс. руб.
6.
СЛОВЕСНО-ФОРМУЛЬНОЕ ОПИСАНИЕАЛГОРИТМОВ
Словесно-формульное описание алгоритма решения примера 1:
1. Ввести ST, перейти к п.2
2. Если ST<5, то ZP:=130к, перейти к п.4, иначе – перейти к п.3
3. Если ST≤15, то ZP:=180к, перейти к п.4, иначе ZP:=180к+(ST15)*10к, перейти к п.4
4. Вывести на экран значение ZP, перейти к п.5
5. Вычисления закончить
7.
ГРАФИЧЕСКОЕ ОПИСАНИЕ АЛГОРИТМАОписание с помощью схем алгоритмов
Схема алгоритма представляет собой систему связанных
геометрических фигур.
Каждая фигура обозначает один этап процесса решения
задачи и называется блоком.
Порядок выполнения указывается стрелками,
соединяющими блоки.
8.
ГРАФИЧЕСКОЕ ОПИСАНИЕ АЛГОРИТМАОперация присваивания изображается прямоугольником (блок
"Процесс")
X=Y+2
9.
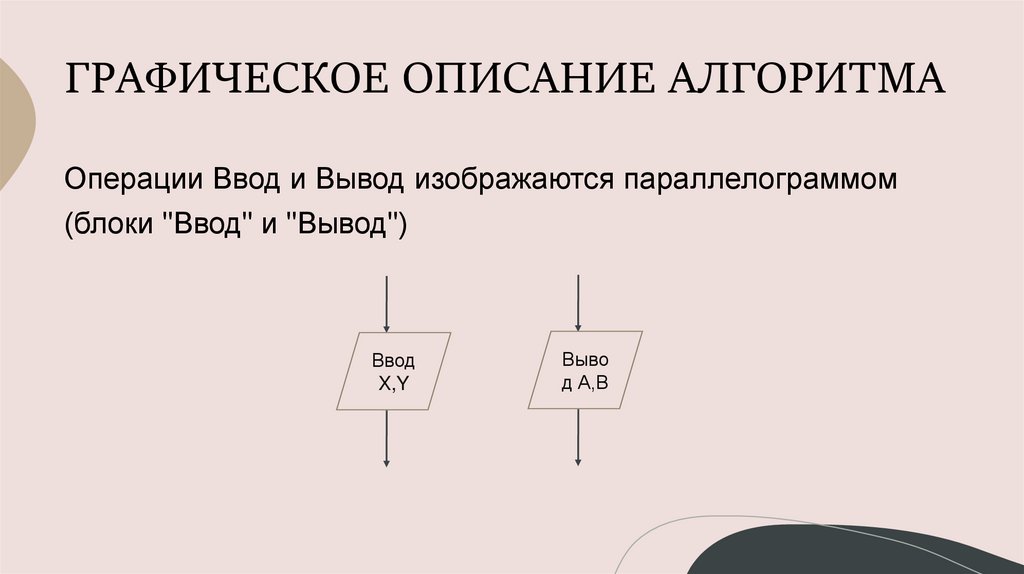
ГРАФИЧЕСКОЕ ОПИСАНИЕ АЛГОРИТМАОперации Ввод и Вывод изображаются параллелограммом
(блоки "Ввод" и "Вывод")
Ввод
X,Y
Выво
д A,B
10.
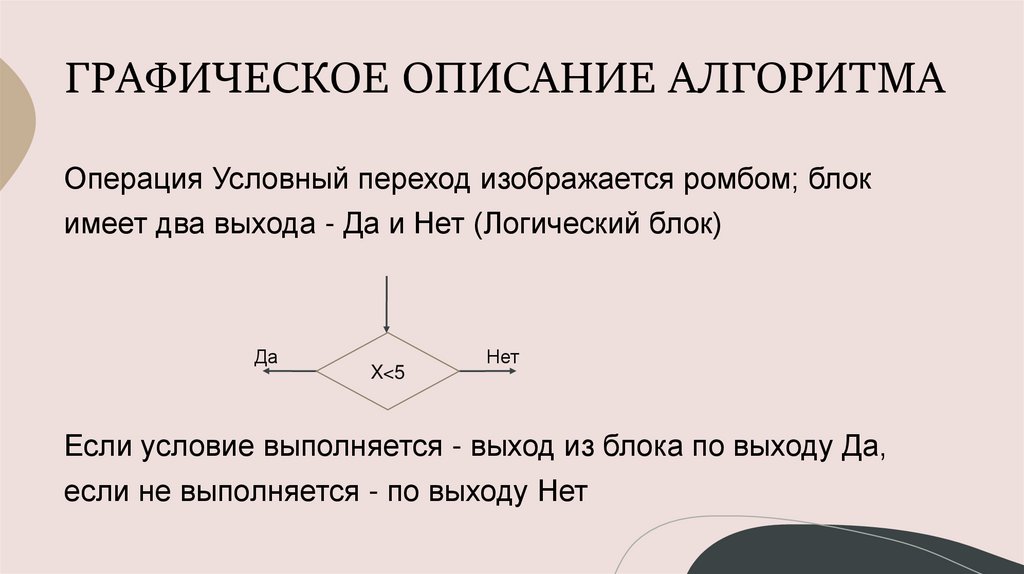
ГРАФИЧЕСКОЕ ОПИСАНИЕ АЛГОРИТМАОперация Условный переход изображается ромбом; блок
имеет два выхода - Да и Нет (Логический блок)
Да
X<5
Нет
Если условие выполняется - выход из блока по выходу Да,
если не выполняется - по выходу Нет
11.
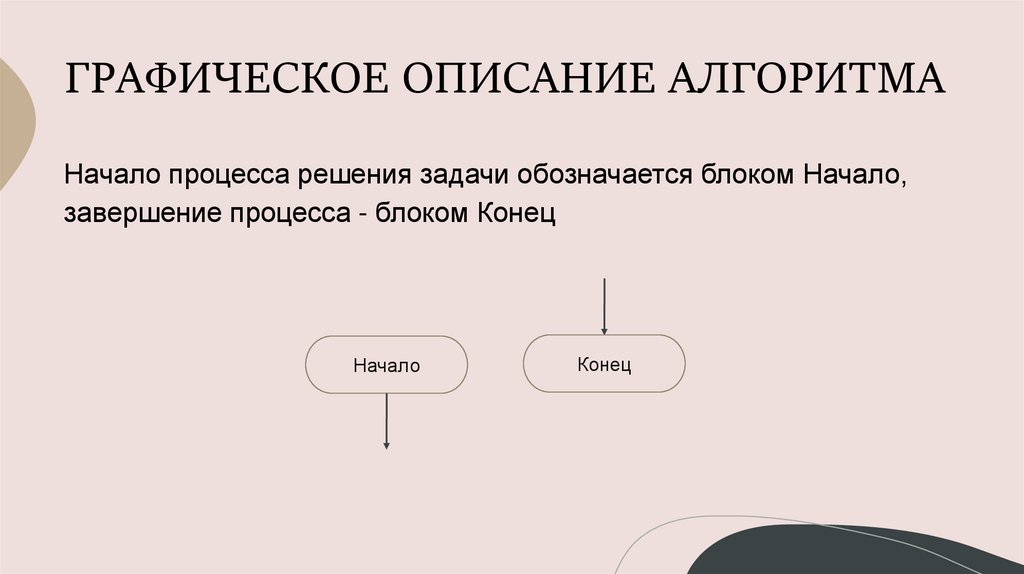
ГРАФИЧЕСКОЕ ОПИСАНИЕ АЛГОРИТМАНачало процесса решения задачи обозначается блоком Начало,
завершение процесса - блоком Конец
Начало
Конец
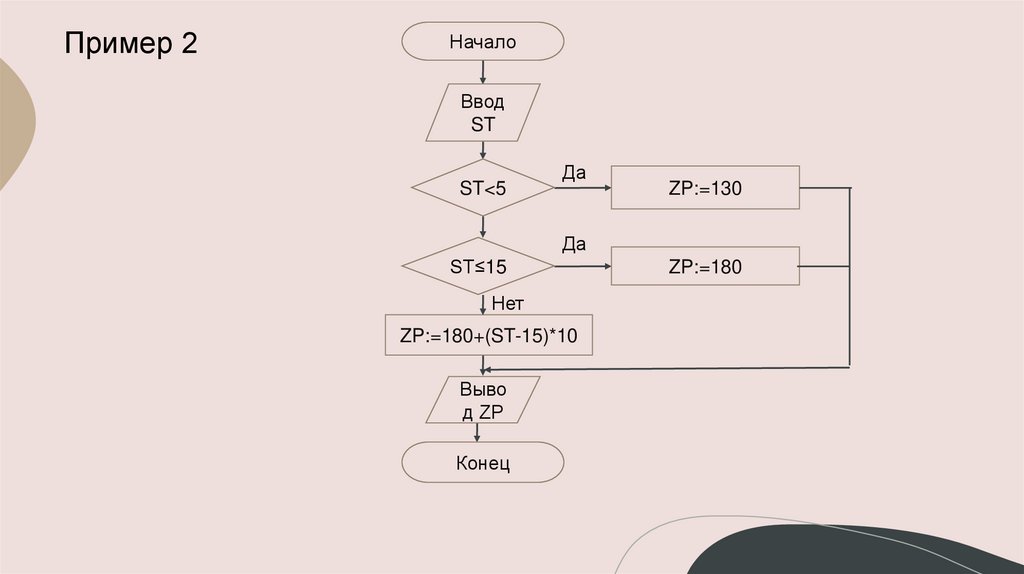
12.
Пример 2Начало
Ввод
ST
ST<5
Да
ZP:=130
Да
ST≤15
Нет
ZP:=180+(ST-15)*10
Выво
д ZP
Конец
ZP:=180
13.
ОПИСАНИЕ АЛГОРИТМОВ НААЛГОРИТМИЧЕСКОМ ЯЗЫКЕ
Алгоритмический язык - это средство для записи
алгоритмов в аналитическом виде, промежуточном между
записью алгоритма на естественном языке и записью на
языке программирования
14.
Пример 3алг зарплата (цел ST, вещ ZP)
арг ST
рез ZP
нач
если ST<5
то ZP:=150
иначе
если ST<=15
то ZP:=180
иначе ZP:=180+(ST-15)10
все
все
конец
15.
ПРАВИЛА ПОСТРОЕНИЯ СХЕМЫАЛГОРИТМА
• Выявить исходные данные, результаты, назначить им имена
• Выбрать метод, порядок решения задачи
• Разбить метод решения задачи на этапы
• Изобразить каждый этап в виде соответствующего блоксхемы алгоритма и указать стрелками порядок из
выполнения
• При любом варианте вычислений предусмотреть: выдачу
результатов, переход к блоку Конец
16.
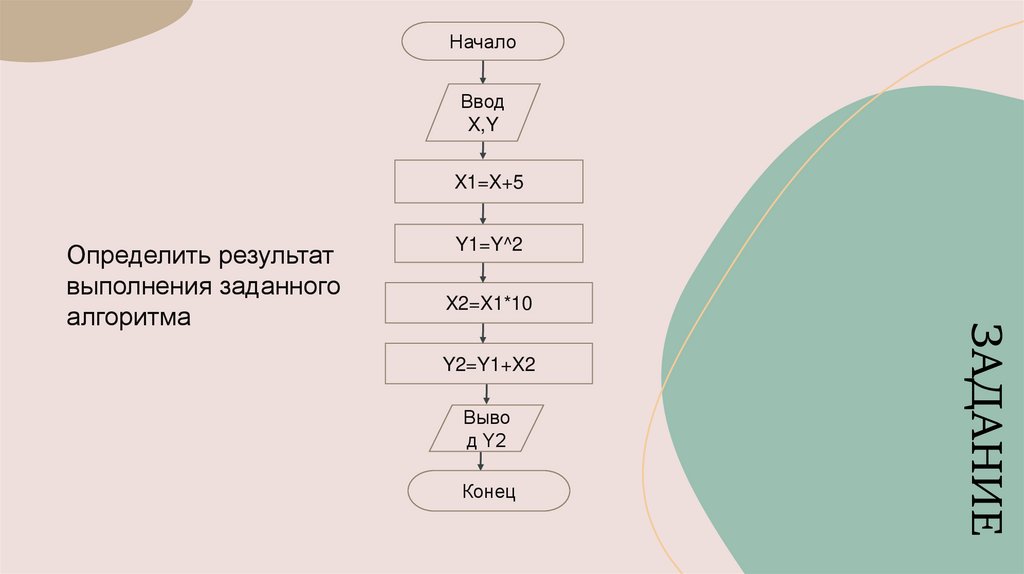
НачалоВвод
X,Y
X1=X+5
X2=X1*10
Y2=Y1+X2
Выво
д Y2
Конец
ЗАДАНИЕ
Определить результат
выполнения заданного
алгоритма
Y1=Y^2
17.
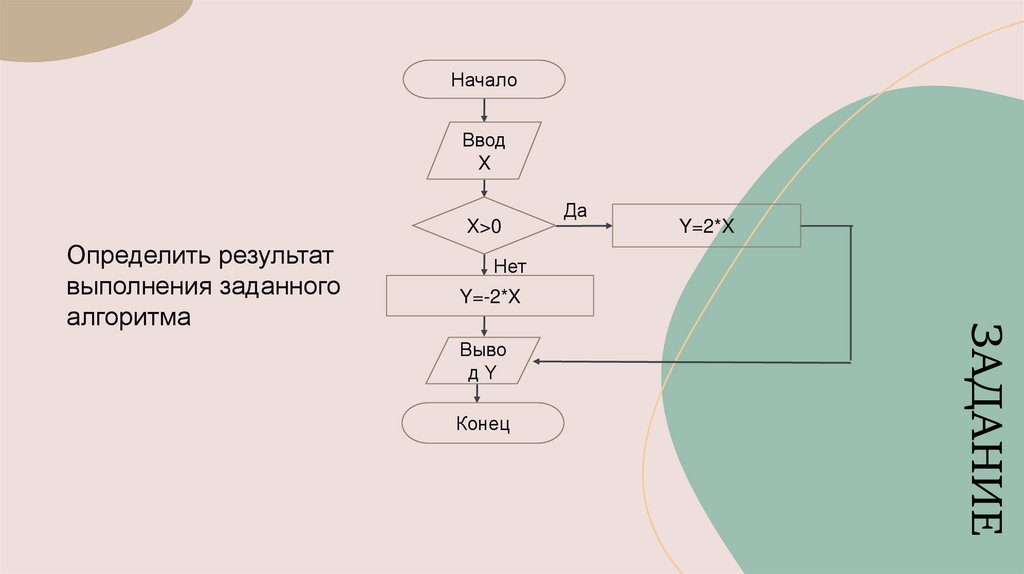
НачалоВвод
X
X>0
Y=2*X
Нет
Y=-2*X
Выво
дY
Конец
ЗАДАНИЕ
Определить результат
выполнения заданного
алгоритма
Да
18.
НачалоВвод
N
N>0
Нет
N<0
M=N+5
Выво
дM
Конец
Да
M=N-10
M=N+10
ЗАДАНИЕ
Определить результат
выполнения заданного
алгоритма
Да
19.
ЗАДАНИЕСоставить алгоритм, который будет решать следующие задачи:
1. Определять является ли число N больше, меньше или
равным нулю
2. Рассчитывать периметр прямоугольника
3. Выдавать крупные или мелкие купюры в банкомате












 informatics
informatics