Пирамида. История изучения

1. ПИРАМИДА

2. Содержание

Определение
2. История изучения
3. Элементы пирамиды
4. Виды пирамид
5. Теорема
6. Основные формулы
7. Задача
1.

3. Определение пирамиды

Пирами́да
это — многогранник,
основание которого — многоугольник,
а остальные грани — треугольники,
имеющие общую вершину. По числу
углов основания различают пирамиды
треугольные, четырёхугольные и т. д.

4. История развития пирамиды в геометрии.

Начало геометрии пирамиды было положено
в Древнем Египте и Вавилоне, однако
активное развитие получило в Древней
Греции. Первые, кто установили чему равен
объем пирамиды, были Евклид и
Демокрит , а доказал этот факт Евдокс
Книдский.
Древнегреческий
математик Евклид систематизировал
знания о пирамиде в XII томе
своих «Начал», а также вывел первое
определение пирамиды: телесная
фигура, ограниченная плоскостями,
которые от одной плоскости сходятся в
одной точке.

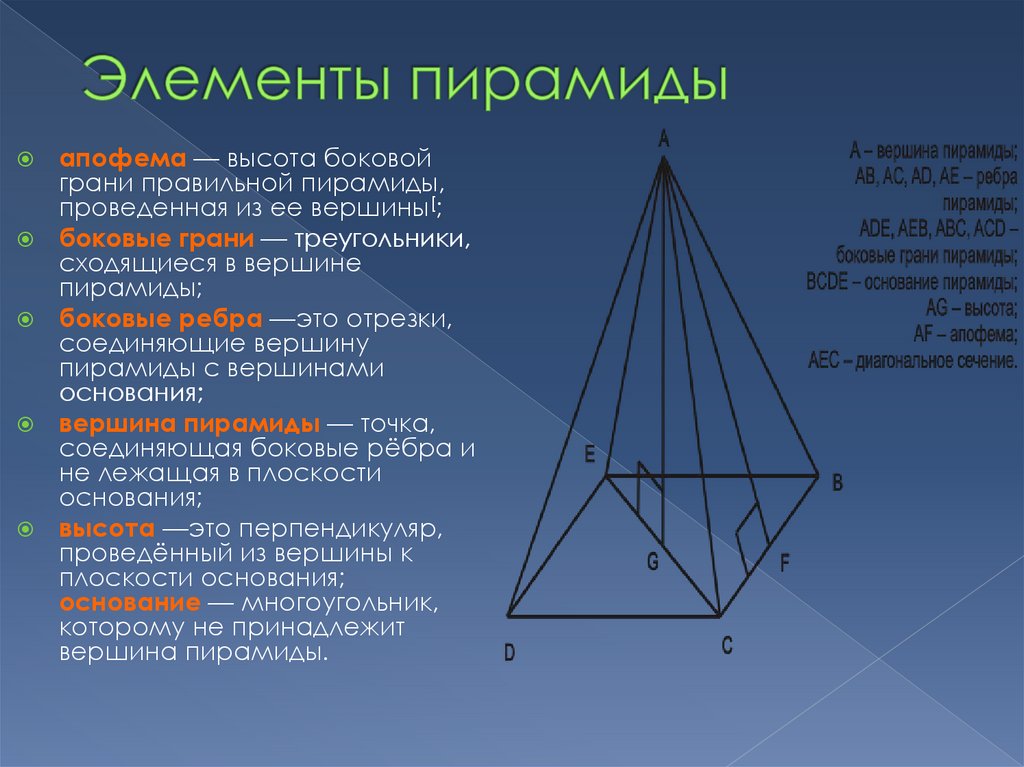
5. Элементы пирамиды

апофема — высота боковой
грани правильной пирамиды,
проведенная из ее вершины[;
боковые грани — треугольники,
сходящиеся в вершине
пирамиды;
боковые ребра —это отрезки,
соединяющие вершину
пирамиды с вершинами
основания;
вершина пирамиды — точка,
соединяющая боковые рёбра и
не лежащая в плоскости
основания;
высота —это перпендикуляр,
проведённый из вершины к
плоскости основания;
основание — многоугольник,
которому не принадлежит
вершина пирамиды.

6. Виды пирамид

1. Наклонная
2. Прямая
3. Правильная
4. Усеченная

7. Наклонная пирамида

Боковые ребра
разной длины
Вершина
пирамиды
проектируется не в
центре основания

8. Прямая пирамида

Противолежащие
боковые ребра
одинаковые
Высота
проектируется в
центре основания

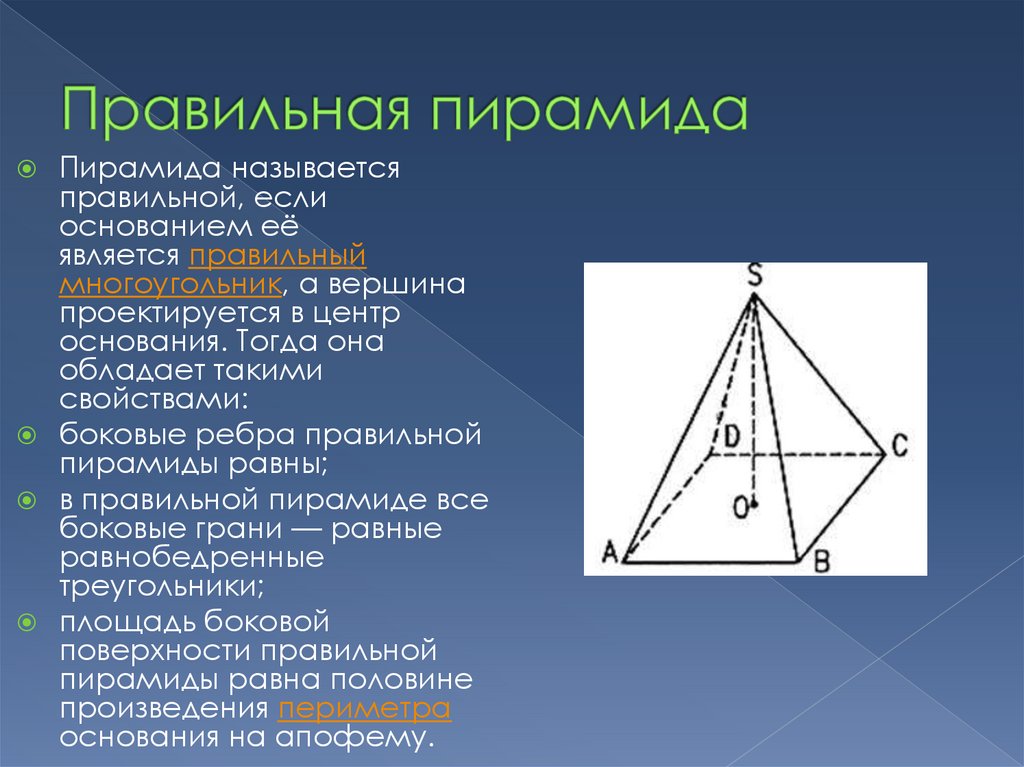
9. Правильная пирамида

Пирамида называется
правильной, если
основанием её
является правильный
многоугольник, а вершина
проектируется в центр
основания. Тогда она
обладает такими
свойствами:
боковые ребра правильной
пирамиды равны;
в правильной пирамиде все
боковые грани — равные
равнобедренные
треугольники;
площадь боковой
поверхности правильной
пирамиды равна половине
произведения периметра
основания на апофему.

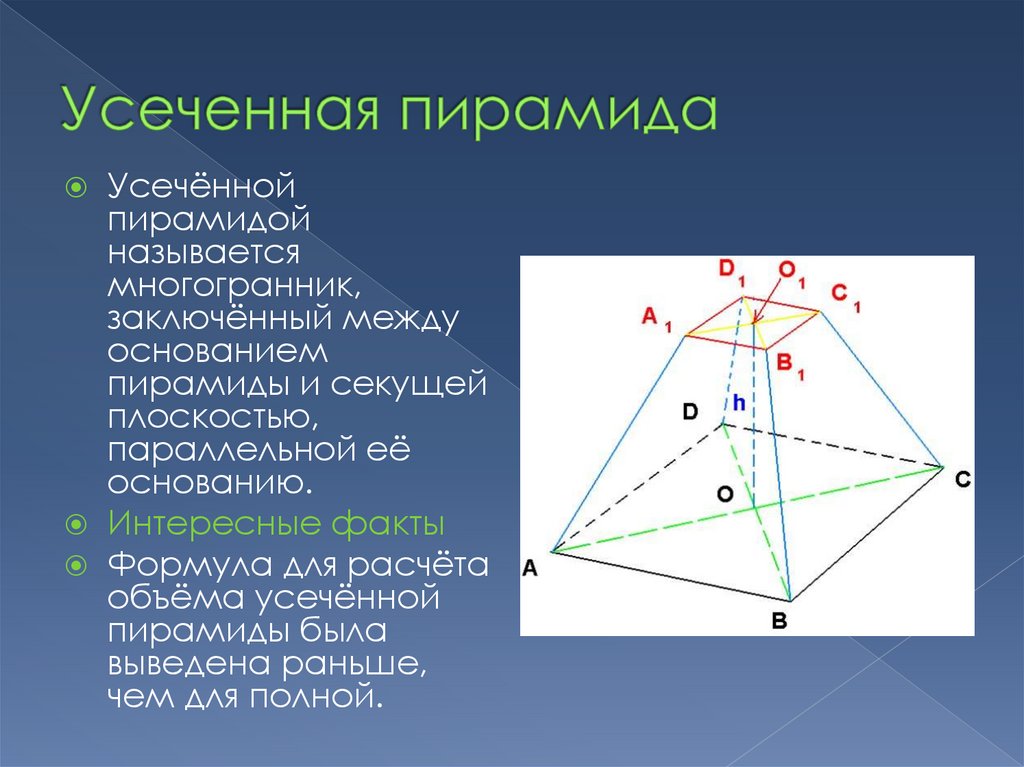
10. Усеченная пирамида

Усечённой
пирамидой
называется
многогранник,
заключённый между
основанием
пирамиды и секущей
плоскостью,
параллельной её
основанию.
Интересные факты
Формула для расчёта
объёма усечённой
пирамиды была
выведена раньше,
чем для полной.

11. Основные формулы