Основные понятия дискретной математики. Операции над множествами. Логика высказываний. Тема 3.1

1.

Тема 3.1.
Основные понятия
дискретной математики.
Операции над
множествами.
Логика высказываний.

2. План:

1. Основное правило комбинаторики.
2. Множества и операции над ними.
3. Элементы математической логики.
4. Понятие графа

3.

1. Основное правило комбинаторики.
Опр. Комбинаторика – один из разделов
дискретной математики, который приобрел
важное значение в связи с использованием его
в теории вероятностей, математической логике,
теории чисел, вычислительной технике,
кибернетики.
Человеку часто приходиться иметь дело с задачами, в которых нужно
подсчитать число всех возможных способов расположения некоторых
предметов или число всех возможных способов осуществления некоторого
действия.
Задачи такого типа называются комбинаторными.

4.

Основное правило комбинаторики (правило
умножения) в общем виде.
Пусть требуется выполнить одно за другим k
действий. Если первое действий можно
выполнить n1 способами, второе действие – n2
способами, третье действие – n3 способами и
так до k-го действия, которое можно выполнить
nk способами, то все k действий вместе могут
быть выполнены n1 n2 n3 ... nk способами

5.

• Пример. Сколько четырехзначных чисел
можно составить из цифр 0, 1, 2, 3, 4, 5 если
ни одна цифра не повторяется более одного
раза.
• Решение. Первую цифру числа можно
выбрать пятью способами (0 не может
стоять в тысячах). Вторую – 5 способами,
третью – 4, четвертую – 3. Согласно правилу
умножения общее число способов равно
5·5·4·3 =300

6.

2. Множества и операции над ними.
Опр. Множество – всякая совокупность элементов
произвольного рода.
Опр. Конечные множества называются те мн-ва, в
которых указано конечное число элементов.
Пример.
1) Мн-во парт в классе – конечное.
2) Мн-во натуральных чисел – бесконечное
Комбинаторика есть теория конечных множеств.
Множества будем обозначать большими латинскими
буквами (А, В, С, …), а их элементы малыми (a, b, c, …).
Количество элементов множества будем обозначать N(А)

7.

Операции над множествами.
Опр. Если А и В – два множества, то множество С,
которому принадлежат те и только те элементы, которые
входят либо в А, либо в В называется объединением
мн-в А и В и обозначается С=А U В
Опр. Если А и В – два множества, то множество С,
которому принадлежат те и только те элементы, которые
являются общими для мн-в А и В называется пересечением
мн-в А и В и обозначается С=А В
Пример.
А = { 1,2,3}; B={ 2,3,4}
А U В = {1,2,3,4}
А В = {2,3}
Опр. Если каждый элемент множества В принадлежит
множеству А ( - знак принадлежности), то В называется
подмножеством множества А и обозначается А В (А
содержит В, В входит в А)

8.

Перестановки данного множества.
Опр. Различные множества, которые отличаются лишь
порядком элементов (т. е. могут быть получены из того же
самого множества), называются перестановками этого
множества.
Пример. Перестановки множества А = {а, Ь, с} из 3
элементов имеют вид (а, b, с), (а, с, b), (b, а, с), (b, с, а), (с, а,
b), (с, b, а).
Теорема 1.Число перестановок множества А, можно найти
по формуле Рn=n!, где множество А имеет п элементов, а Рn
- число перестановок.
n!= 1*2*3*…*n
Пример.
Сколькими способами можно разместить на полке 4 книги?
Решение. Искомое число способов равно числу способов
упорядочения множества, состоящего из 4 элементов, т. е.
Р4 = 1 • 2 • 3 • 4 = 24.

9.

Сочетание данного множества.
Опр. 8. Произвольное k-элементное
подмножество n-элементного множества
называется сочетанием из n элементов по k.
Теорема 2. Число сочетаний из п элементов по
n!
k, равно C nk
k! (n k )!
Пример. Сколькими способами читатель может
выбрать 3 книжки из 5?
Решение. Искомое число способов равно числу
трехэлементных подмножеств множества из 5
элементов: С 3 5! 10
5
3! 2!

10.

Размещения данного множества.
Рассмотрим теперь подмножества данного множества А.
Число всех k-элементных подмножеств множества А равно Сkn.
Каждое такое подмножество можно упорядочить k! способами.
Таким образом получим все упорядоченные k-элементные
подмножества множества А. Следовательно, их число будет k! C nk
Теорема 3. Число упорядоченных k-элементных подмножеств
множества, состоящего из п элементов, равно
n!
Ank k! C nk
n (n 1) ... (n k 1)
(n k )!
Опр.9. Упорядоченные k-элементные подмножества
множества из п элементов называются размещениями
из п элементов по k. Различные размещения из n по k
отличаются количеством элементов либо их порядком.
Следовательно, число различных размещений из п по k равно
Ank n (n 1) ... (n k 1)
Пример. Сколькими способами можно рассадить 4 учащихся на 25 местах?
Решение. Искомое число способов равно числу размещений из 25 по 4:
4
A25
25 24 23 22 303600

11.

3. Элементы математической логики.
Опр. Высказыванием называется повествовательное
предложение относительно которого можно говорить истинно
оно или ложно.
И, Л – значение истинности высказываний.
А: 5+3=8; А = И
В: 1+4=2; В = Л
Операции.
1) Отрицание высказывания А называется высказывание
А (не А), которое истинно тогда и только тогда,
когда (т. и т. т., к) А ложно.
Таблица истинности.
А
И
Л
А
Л
И

12.

2) Конъюнкция высказываний А, В называется
высказывание А В (А и В), которое истинно
т. и т. т., к истины оба высказывания А и В
Таблица истинности.
А
В
А В
И
И
И
И
Л
Л
Л
И
Л
Л
Л
Л

13.

3) Дизъюнкция высказываний А, В называется
высказывание А В (А или В), которое истинно
т. и т. т., к истинно хотя бы одно из высказываний А или В
Таблица истинности.
А
В
А В
И
И
И
И
Л
И
Л
И
И
Л
Л
Л

14.

4. Понятие графа
ТЕОРИЯ ГРАФОВ - это область дискретной математики,
особенностью, которой является геометрический подход
к изучению объектов.
Основные определения и теоремы об элементах
теории графов.
Графом называется совокупность конечного числа точек,
называемых вершинами графа, и попарно соединяющих
некоторые из этих вершин линий, называемых ребрами
или дугами графа.
Графом называется непустое множество точек (вершин)
и отрезков (ребер), оба конца которых принадлежат
заданному множеству точек.
Вершины графа, которые не принадлежат ни одному
ребру, называются изолированными.
1
2
3
Вершина 2 – изолированная.

15.

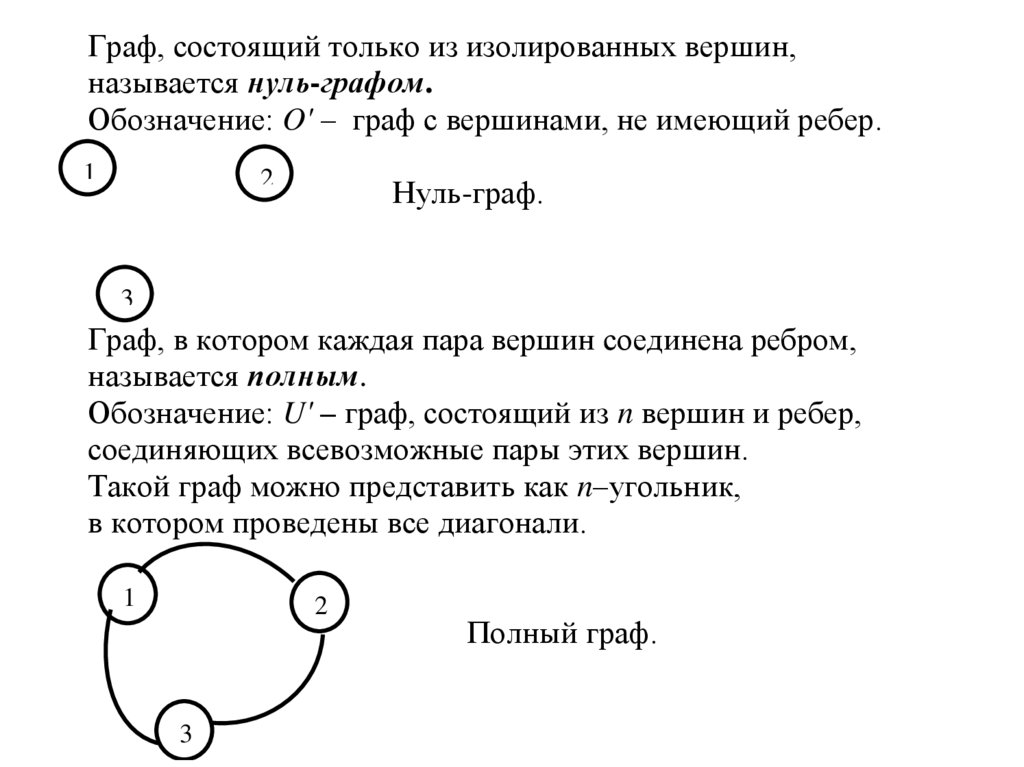
Граф, состоящий только из изолированных вершин,
называется нуль-графом.
Обозначение: O' – граф с вершинами, не имеющий ребер.
1
2
Нуль-граф.
3
Граф, в котором каждая пара вершин соединена ребром,
называется полным.
Обозначение: U' – граф, состоящий из n вершин и ребер,
соединяющих всевозможные пары этих вершин.
Такой граф можно представить как n–угольник,
в котором проведены все диагонали.
1
2
3
Полный граф.

16.

Степенью вершины называется число ребер, которым
принадлежит вершина.
Обозначение: p (1) – степень вершины 1.
Например, p(1)=2, p(2)=2, p(3)=2,
Многоугольник плоского графа,
1
2
не содержащий внутри себя никаких
вершин или ребер графа, называют его гранью.
Циклом называется путь, в котором совпадают
начальная и конечная точка.
3
Вот пример цикла, проложенного
на графе G: (1, 2); (2, 3); (3, 1).
Простым циклом называется цикл, не проходящий ни через одну
из вершин графа более одного раза.

17.

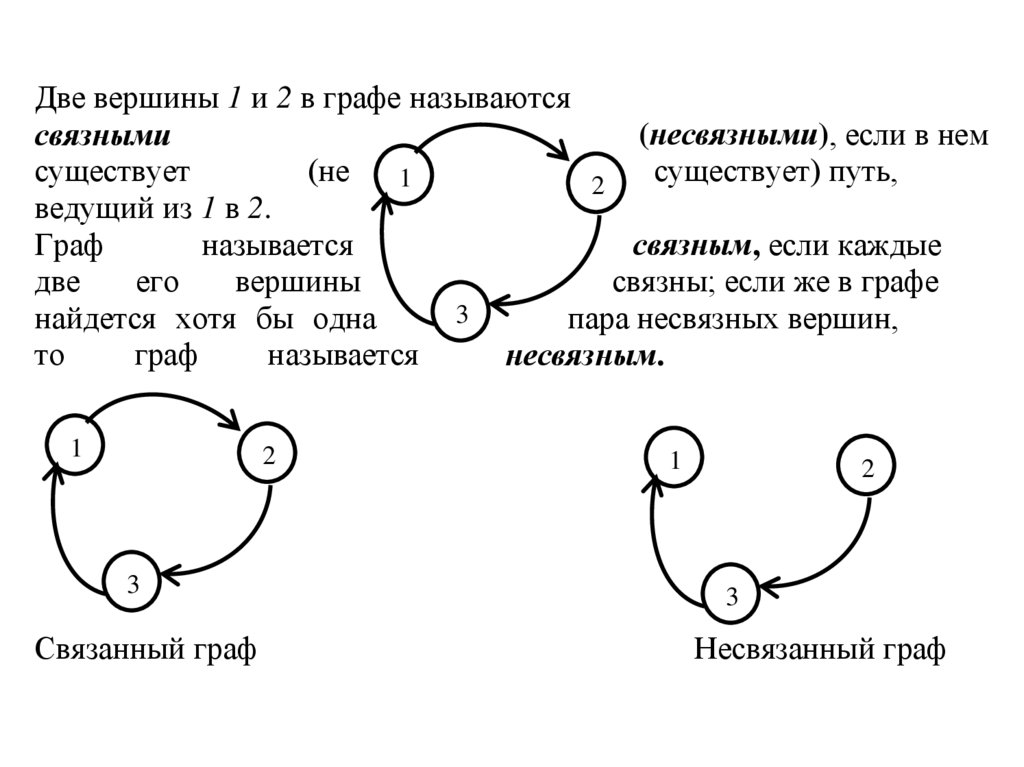
Две вершины 1 и 2 в графе называются
(несвязными), если в нем
связными
существует
(не
существует) путь,
1
2
ведущий из 1 в 2.
Граф
называется
связным, если каждые
две
его
вершины
связны; если же в графе
3
найдется хотя бы одна
пара несвязных вершин,
то
граф
называется
несвязным.
1
2
3
Связанный граф
1
2
3
Несвязанный граф

18.

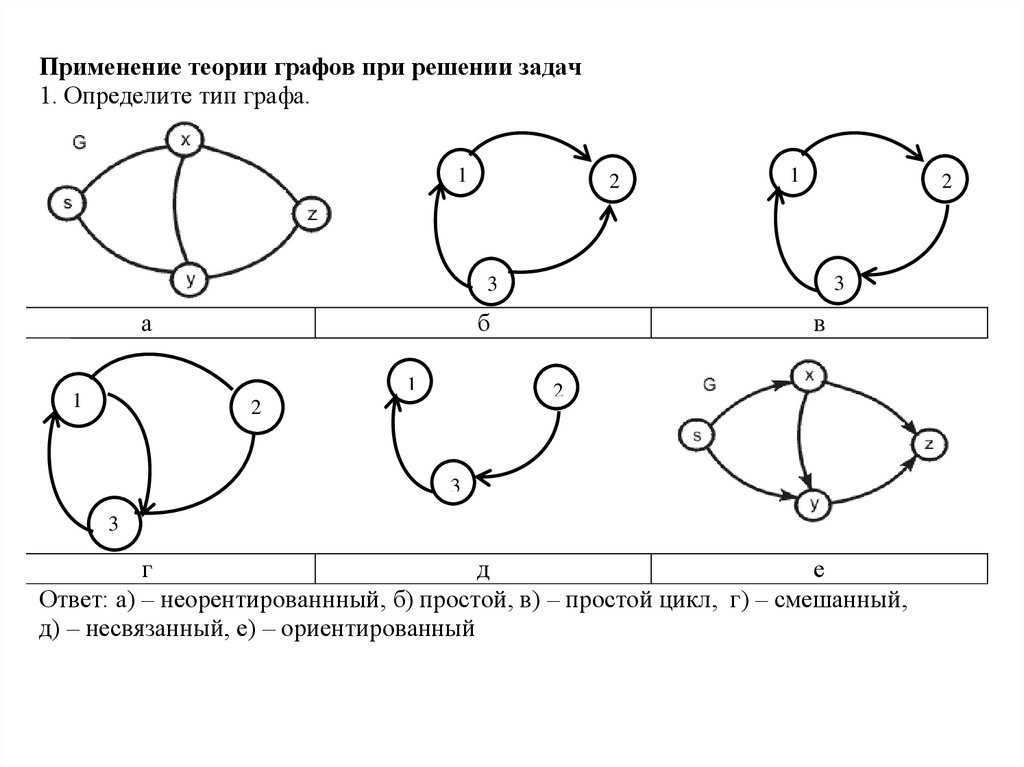
Применение теории графов при решении задач
1. Определите тип графа.
1
2
1
2
3
3
а
б
1
1
в
2
2
3
3
г
д
е
Ответ: а) – неорентированнный, б) простой, в) – простой цикл, г) – смешанный,
д) – несвязанный, е) – ориентированный

19.

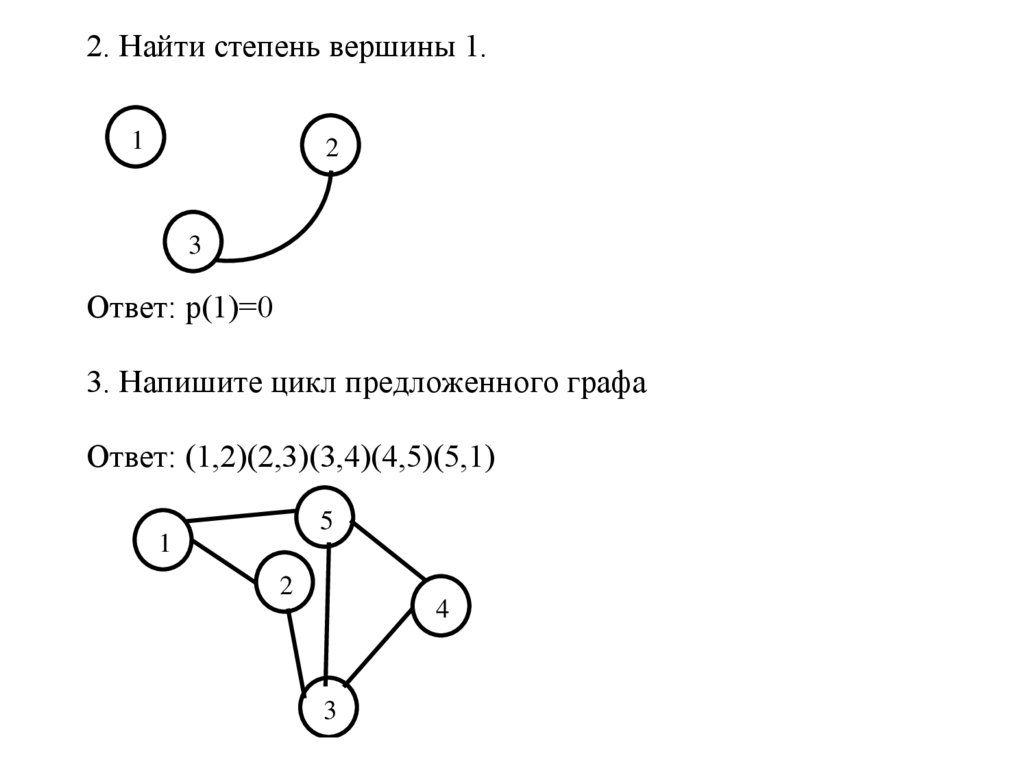
2. Найти степень вершины 1.
1
2
3
Ответ: р(1)=0
3. Напишите цикл предложенного графа
Ответ: (1,2)(2,3)(3,4)(4,5)(5,1)
5
1
2
4
3