Similar presentations:
Введение в многомерную статистику. Лекция 12
1. ЛЕКЦИЯ 12
ВВЕДЕНИЕ ВМНОГОМЕРНУЮ
СТАТИСТИКУ
2. 12.1. Понятие о многомерной совокупности
3. Многомерная матрица данных размером n*m:
х1 х2 х3 … хnу1 … … … … …
у2 … … … … …
у3
…
уm
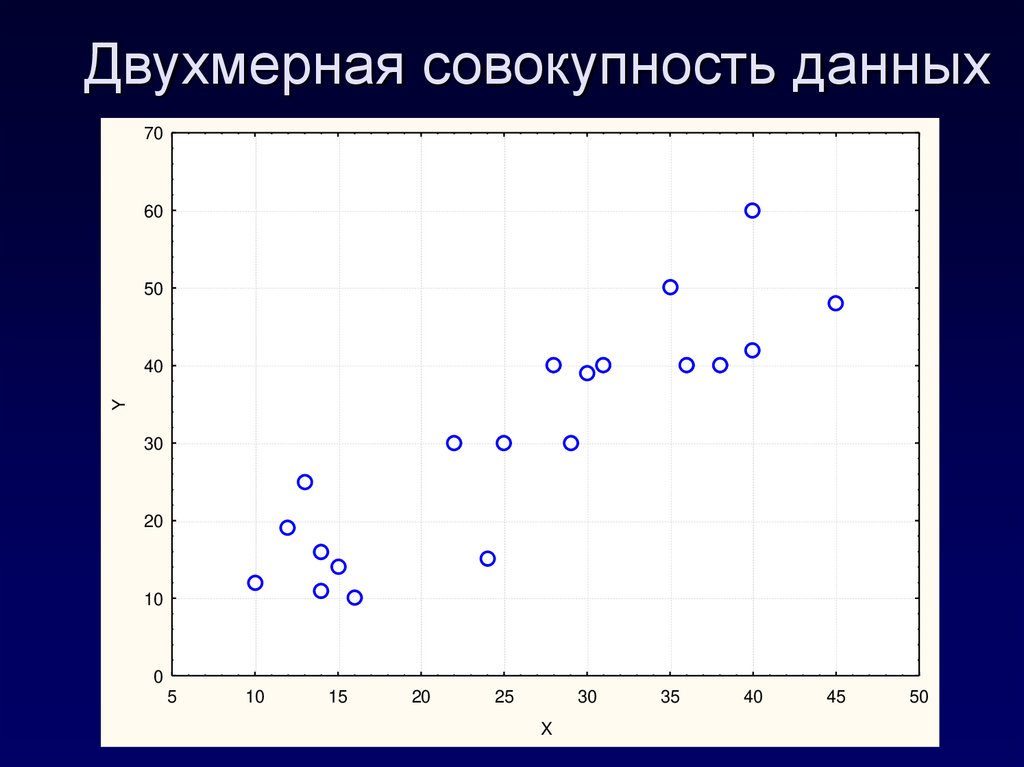
4. Двухмерная совокупность данных
7060
50
Y
40
30
20
10
0
5
10
15
20
25
30
X
35
40
45
50
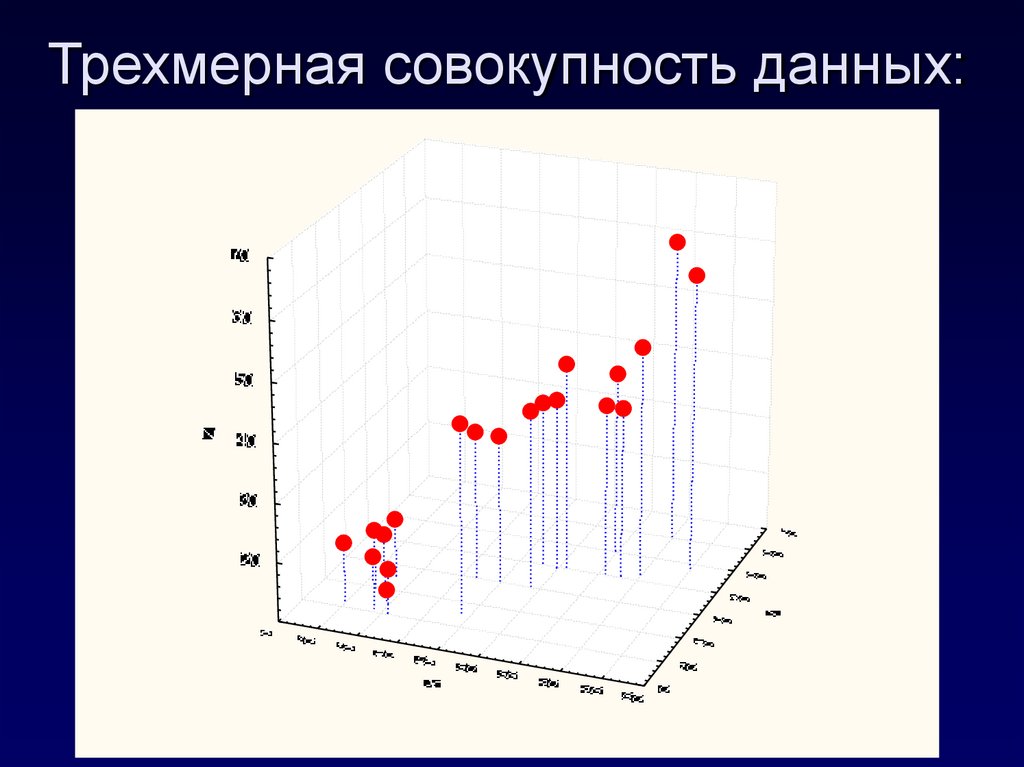
5. Трехмерная совокупность данных:
6. Наиболее распространенные методы многомерного анализа:
• Кластерный анализ (ClusterAnalysis);
• Дискриминантный анализ
(Discriminant Analysis);
• Компонентный анализ (=анализ
главных компонент) (Principal
Components Analysis, РСА)
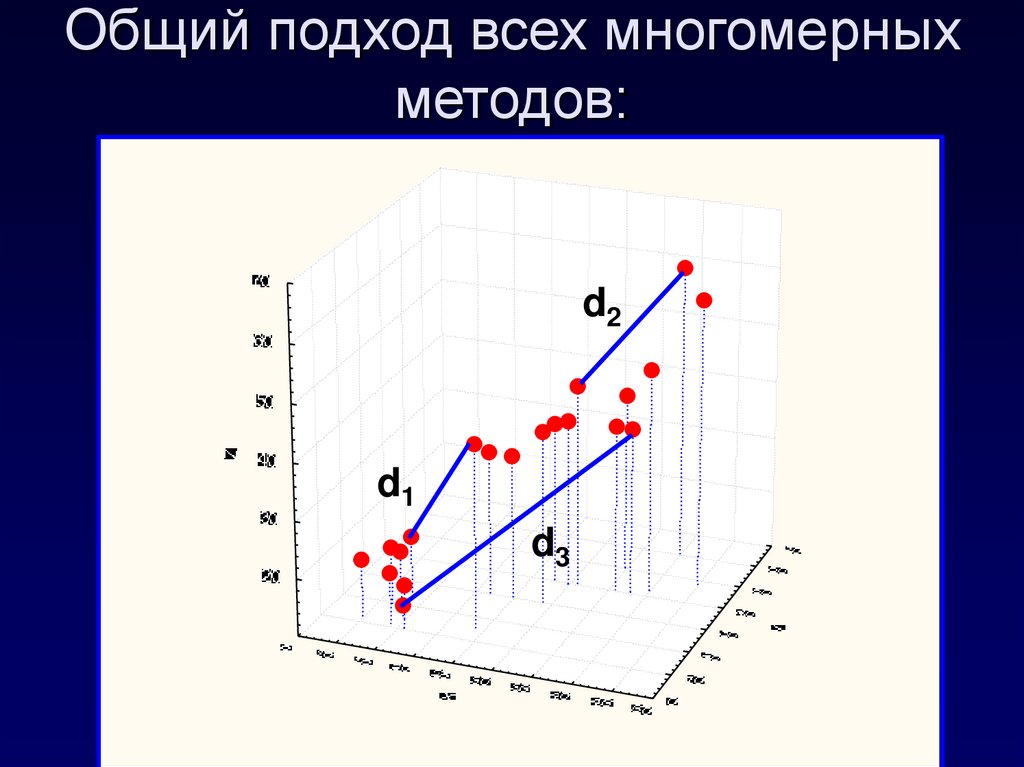
7. Общий подход всех многомерных методов:
d2d1
d3
8. 12.2. Кластерный анализ
9. Евклидова мера расстояния между объектами:
d jk(
x
x
)
ij ik
2
M
xij и xik – значения i-го признака у j-го и k-го
объектов, М – число учитываемых
признаков.
10. Евклидово расстояние (Euclidian distance):
S2S1
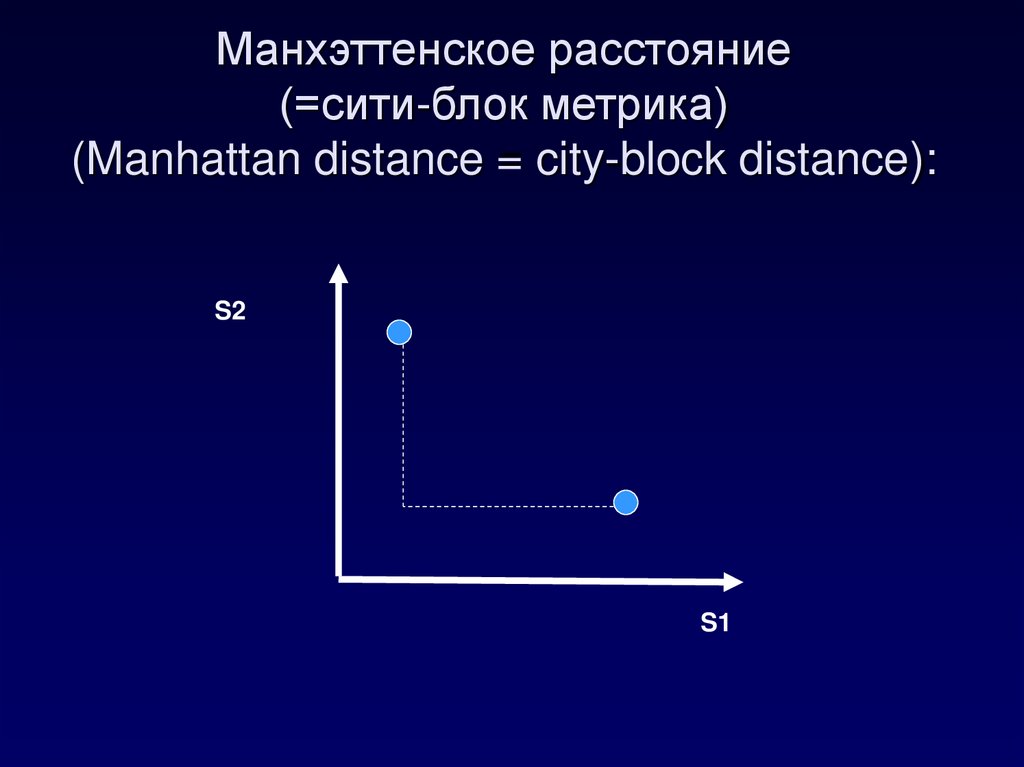
11. Манхэттенское расстояние (=сити-блок метрика) (Manhattan distance = city-block distance):
S2S1
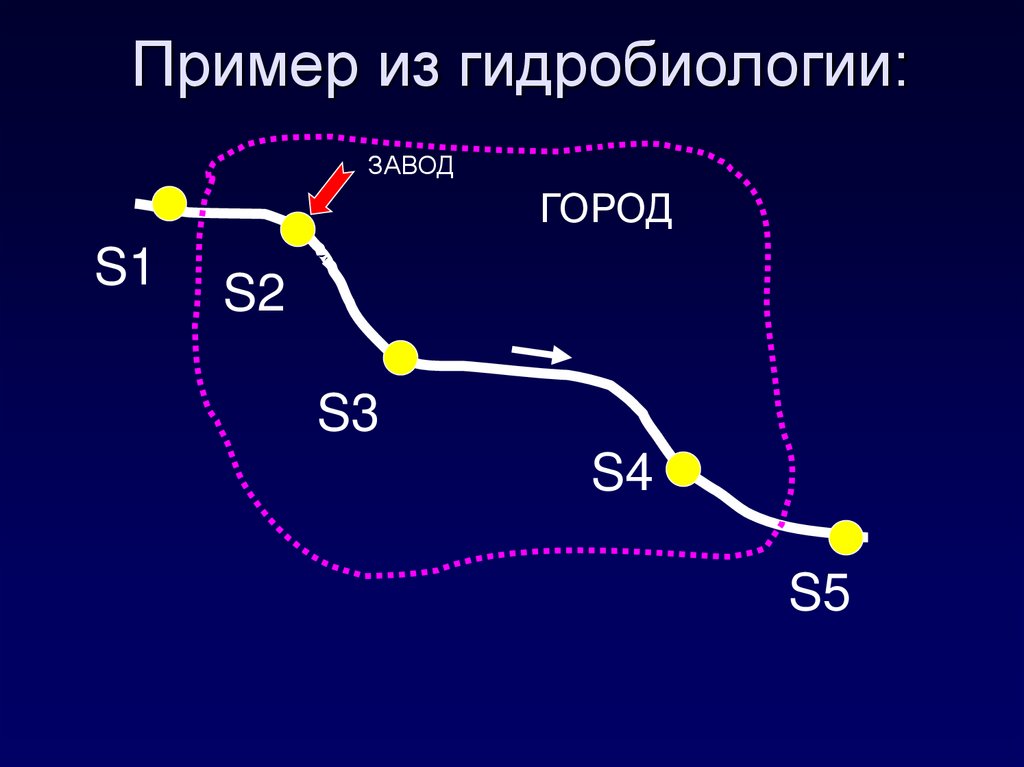
12. Пример из гидробиологии:
ЗАВОДГОРОД
S1
S2
S3
S4
S5
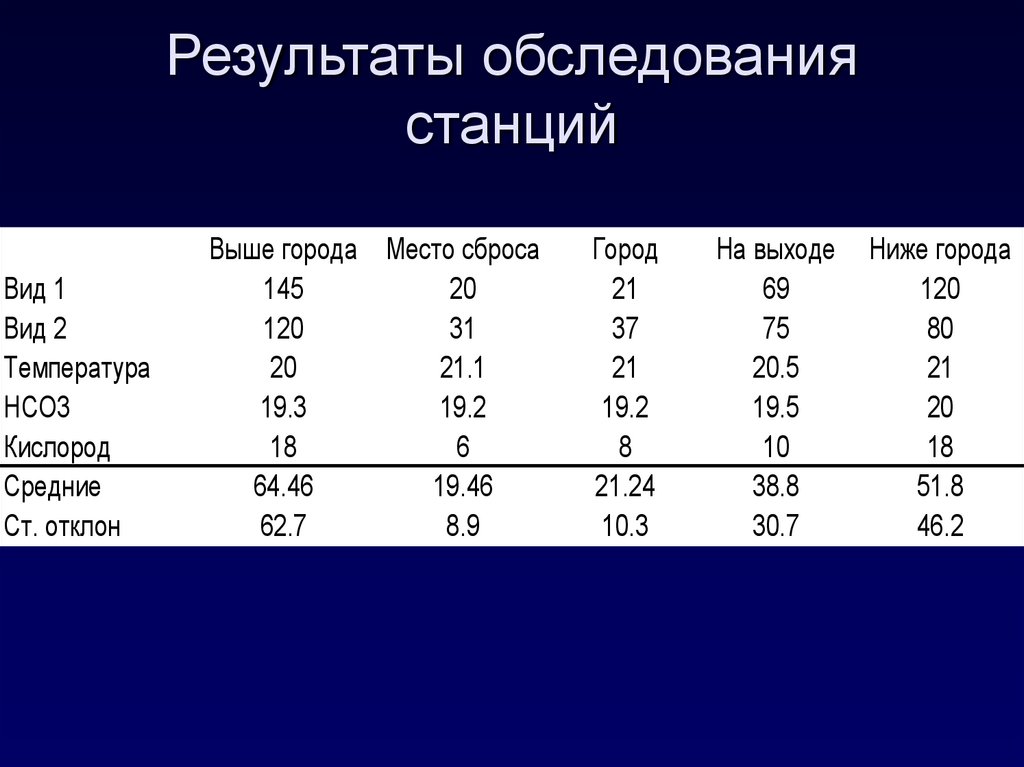
13. Результаты обследования станций
Вид 1Вид 2
Температура
HCO3
Кислород
Средние
Ст. отклон
Выше города Место сброса
145
20
120
31
20
21.1
19.3
19.2
18
6
64.46
19.46
62.7
8.9
Город
21
37
21
19.2
8
21.24
10.3
На выходе
69
75
20.5
19.5
10
38.8
30.7
Ниже города
120
80
21
20
18
51.8
46.2
14. Стандартизация матрицы:
xi xx
s
x 0 s 1
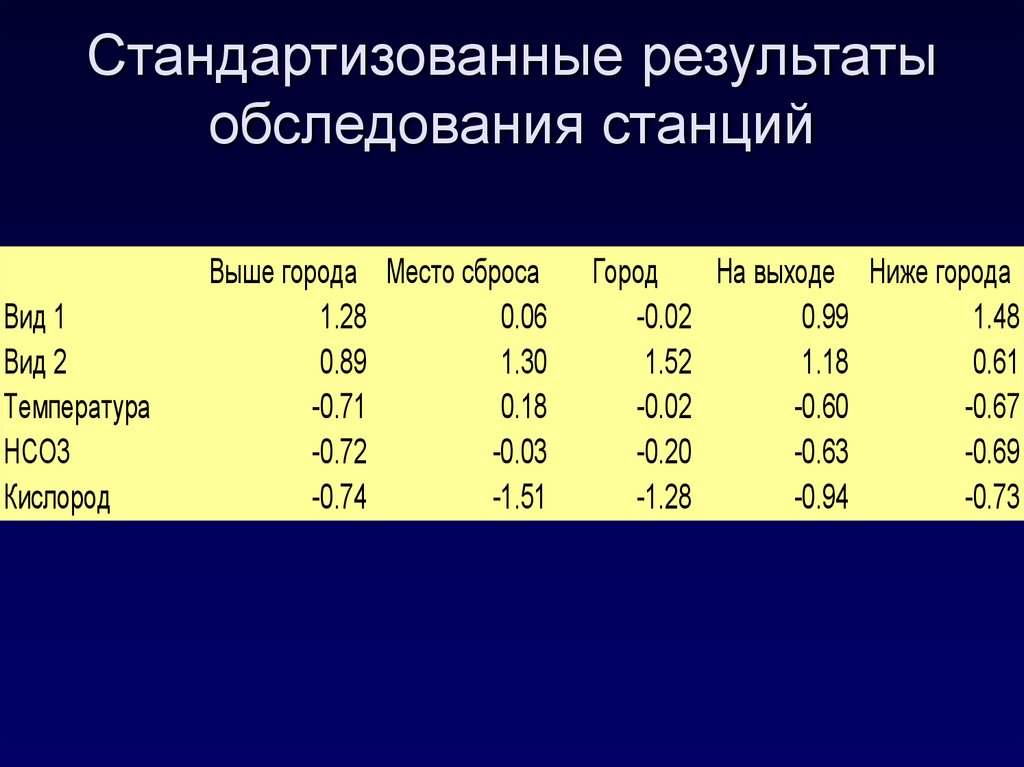
15. Стандартизованные результаты обследования станций
Вид 1Вид 2
Температура
HCO3
Кислород
Выше города Место сброса
1.28
0.06
0.89
1.30
-0.71
0.18
-0.72
-0.03
-0.74
-1.51
Город
На выходе Ниже города
-0.02
0.99
1.48
1.52
1.18
0.61
-0.02
-0.60
-0.67
-0.20
-0.63
-0.69
-1.28
-0.94
-0.73
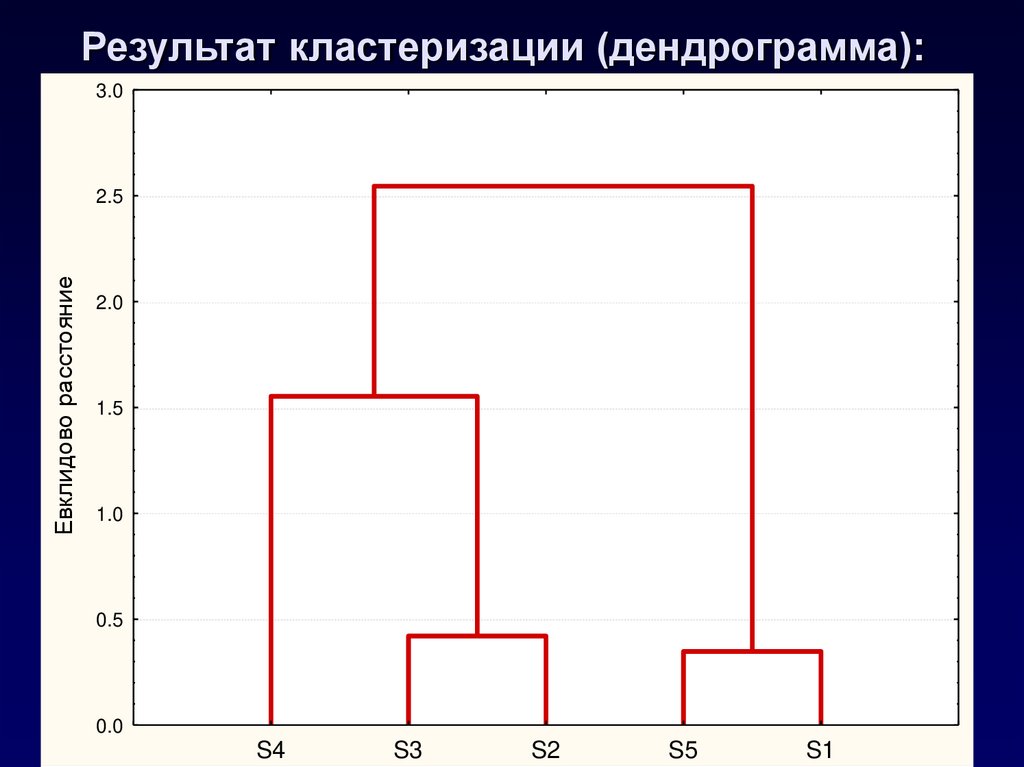
16. Результат кластеризации (дендрограмма):
3.0Евклидово расстояние
2.5
2.0
1.5
1.0
0.5
0.0
S4
S3
S2
S5
S1
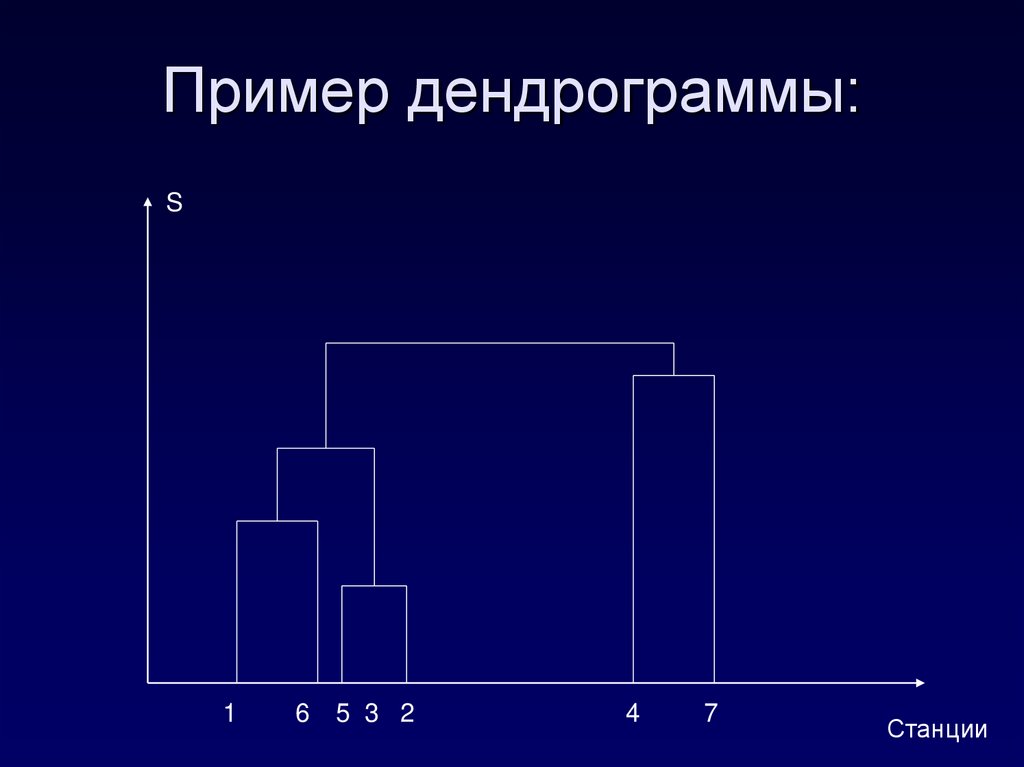
17. Пример дендрограммы:
S1
6
5 3 2
4
7
Станции
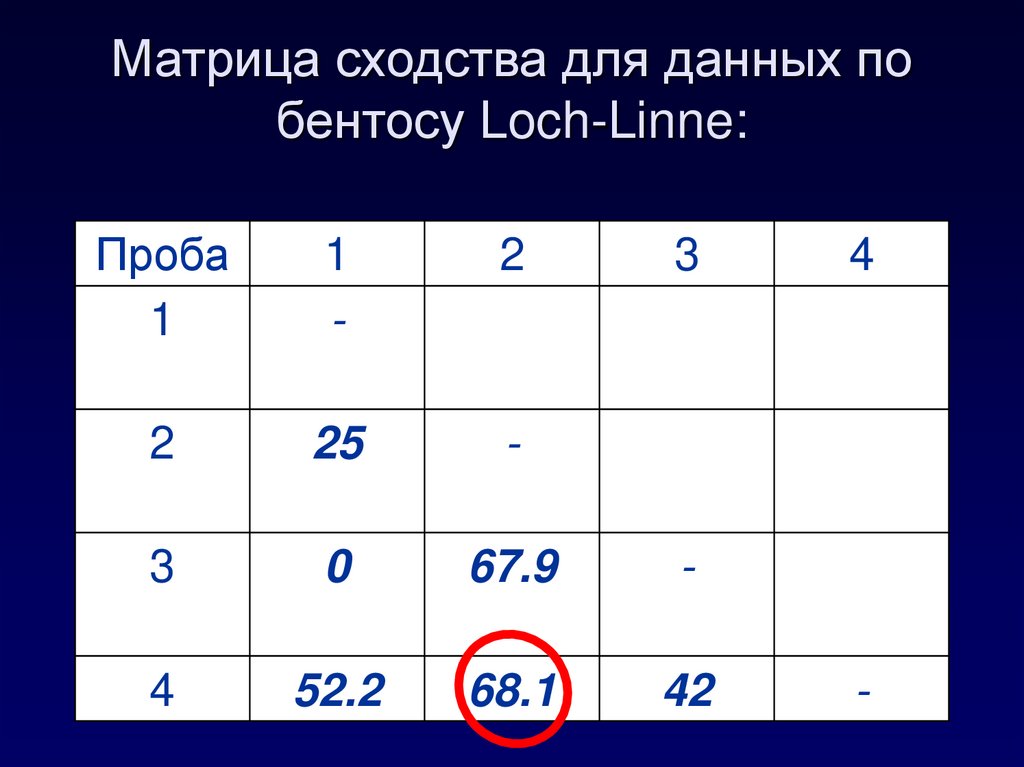
18. Матрица сходства для данных по бентосу Loch-Linne:
Проба1
1
-
2
2
25
-
3
0
67.9
-
4
52.2
68.1
42
3
4
-
19. Возможные способы объединения объектов в кластеры:
• одиночное присоединение (singlelinkage): выбирается максимальное из
исходных сходств;
• полное присоединение (complete linkage):
выбирается наименьшее из исходных
сходств;
• среднее присоединение (group-average
linkage): S(1, 2&4) = [S(1,4)+ + S(1,2)]/2 =
38.9%
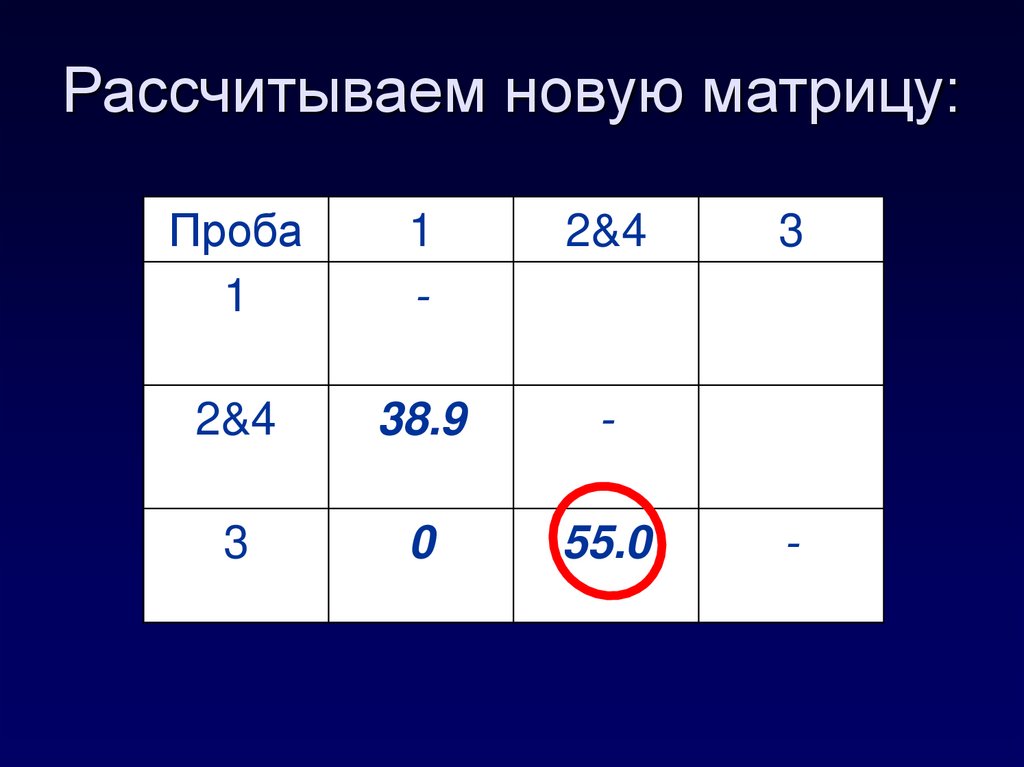
20. Рассчитываем новую матрицу:
Проба1
1
-
2&4
2&4
38.9
-
3
0
55.0
3
-
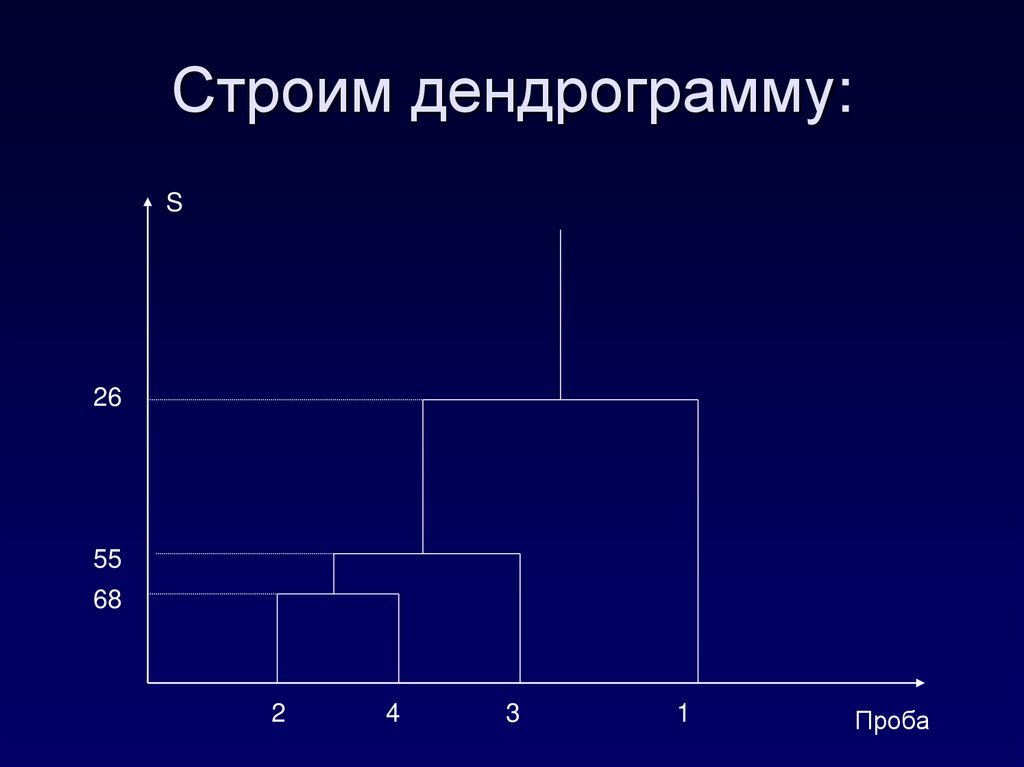
21. Строим дендрограмму:
S26
55
68
2
4
3
1
Проба
22. 12.3. Дискриминантный анализ
23. Задача дискриминантного анализа:
Определить, к какой из двухили более априорно
выделенных групп
принадлежит изучаемый
объект.
24. Визуально самцы и самки у этого вида не различаются; многие морфологические признаки (длина крыла, хвоста, цевки) довольно
сильноперекрываются.
Phylloscopus trochilus
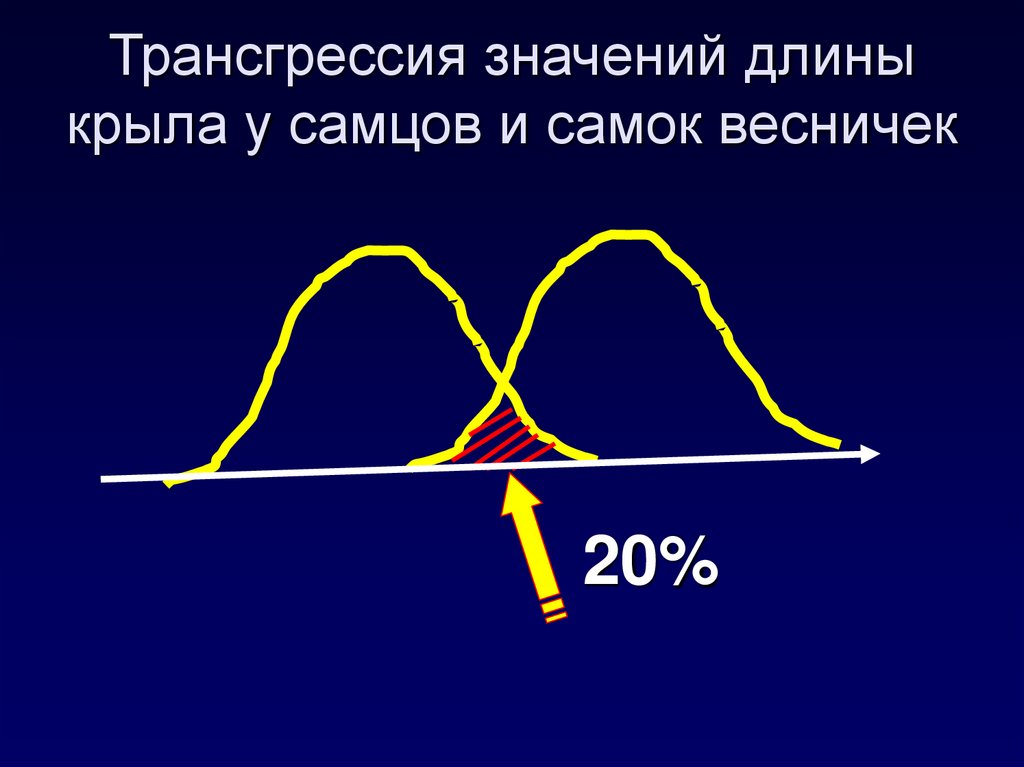
25. Трансгрессия значений длины крыла у самцов и самок весничек
20%26. Трансгрессия значений длины цевки у самцов и самок весничек
90%27. Уравнение дискриминантного анализа для двух признаков:
Z ax by H Z• а и b - «вклад» каждого из признаков в
диагностические возможности функции;
• Н – величина, отражающая степень
трансгрессии распределений Z для самок
и самцов;
• ΔZ - поправка на разные объемы выборок
28. Интерпретация:
• Z < 0 - самка• Z > 0 - самец
29. 12.4. Анализ главных компонент
30.
Ординация - картирование взаимногорасположения станций отбора проб в
особой двух- или трехмерной
системе координат, направленное на
выявление сходств биологических
сообществ на этих станциях.
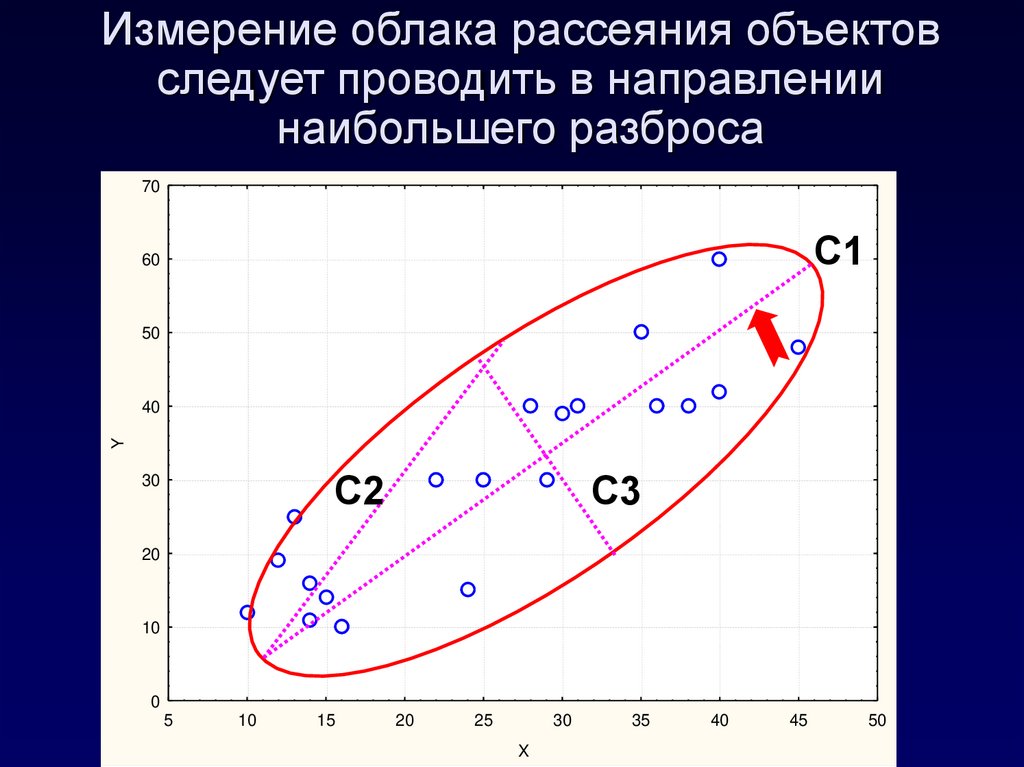
31. Измерение облака рассеяния объектов следует проводить в направлении наибольшего разброса
70С1
60
50
Y
40
С2
30
С3
20
10
0
5
10
15
20
25
30
X
35
40
45
50
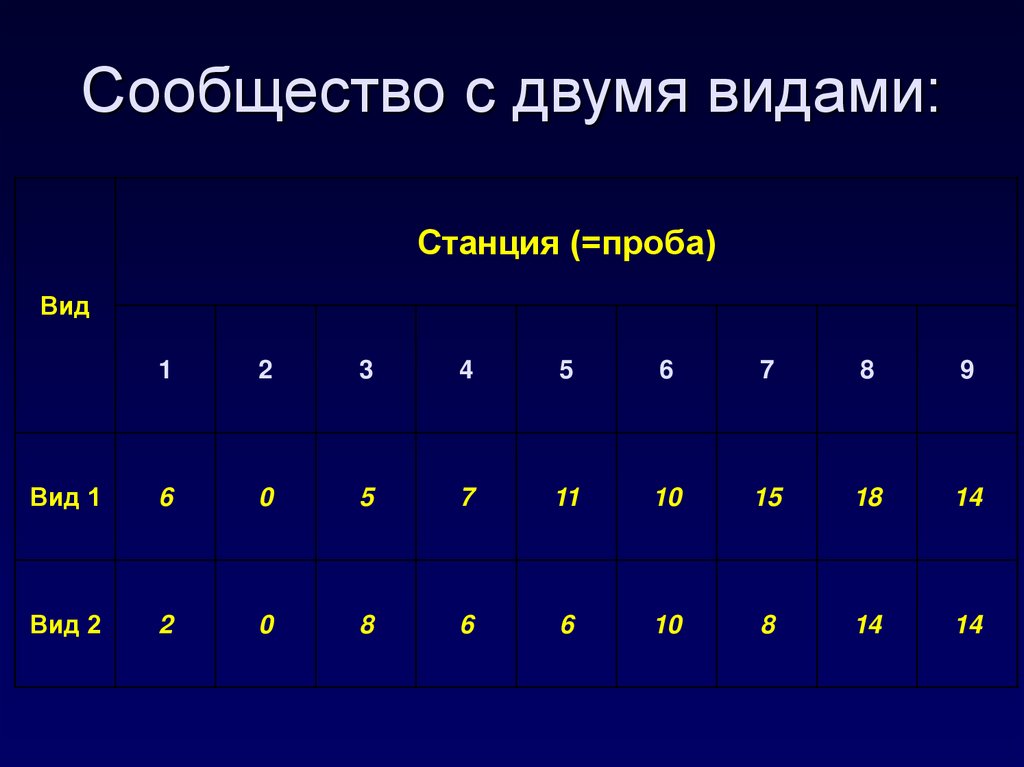
32. Сообщество с двумя видами:
Станция (=проба)Вид
1
2
3
4
5
6
7
8
9
Вид 1
6
0
5
7
11
10
15
18
14
Вид 2
2
0
8
6
6
10
8
14
14
33. Ординация станций в координатах численностей двух видов
Вид 28
9
6
3
4
5
7
1
2
Вид 1
34. Одномерная ординация тех же станций (выполнена путем проецирования точек на ось первого вида)
2314
65
97
8
Вид 1
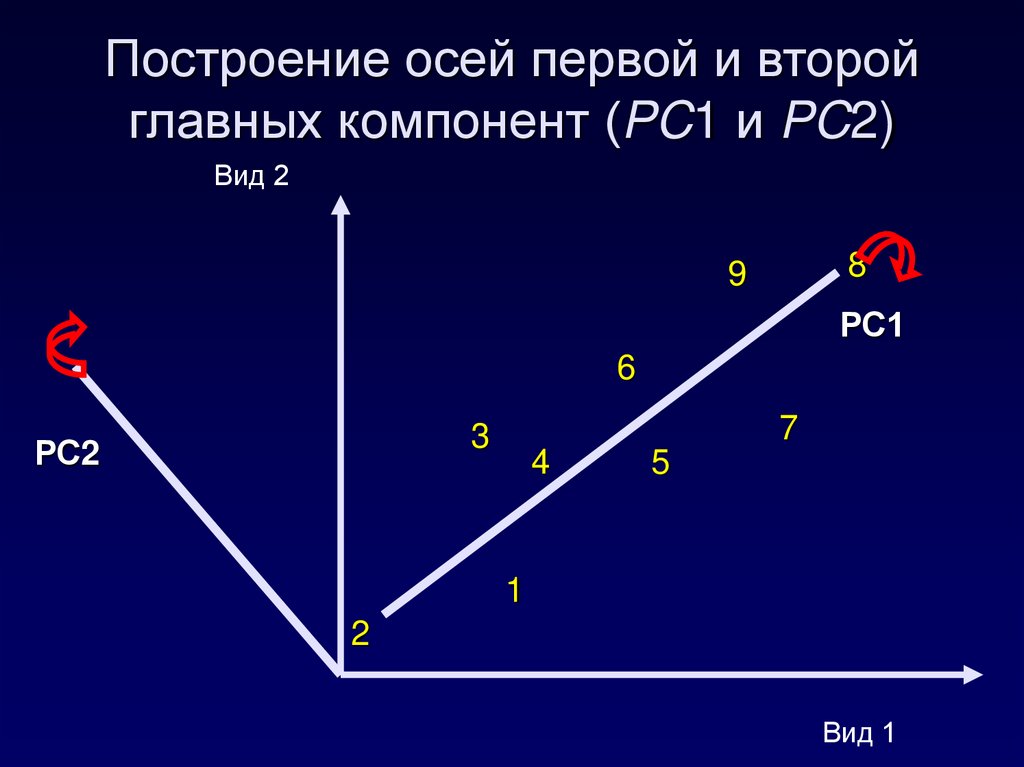
35. Построение осей первой и второй главных компонент (PC1 и PC2)
Вид 28
9
РС1
6
7
3
РС2
4
5
1
2
Вид 1
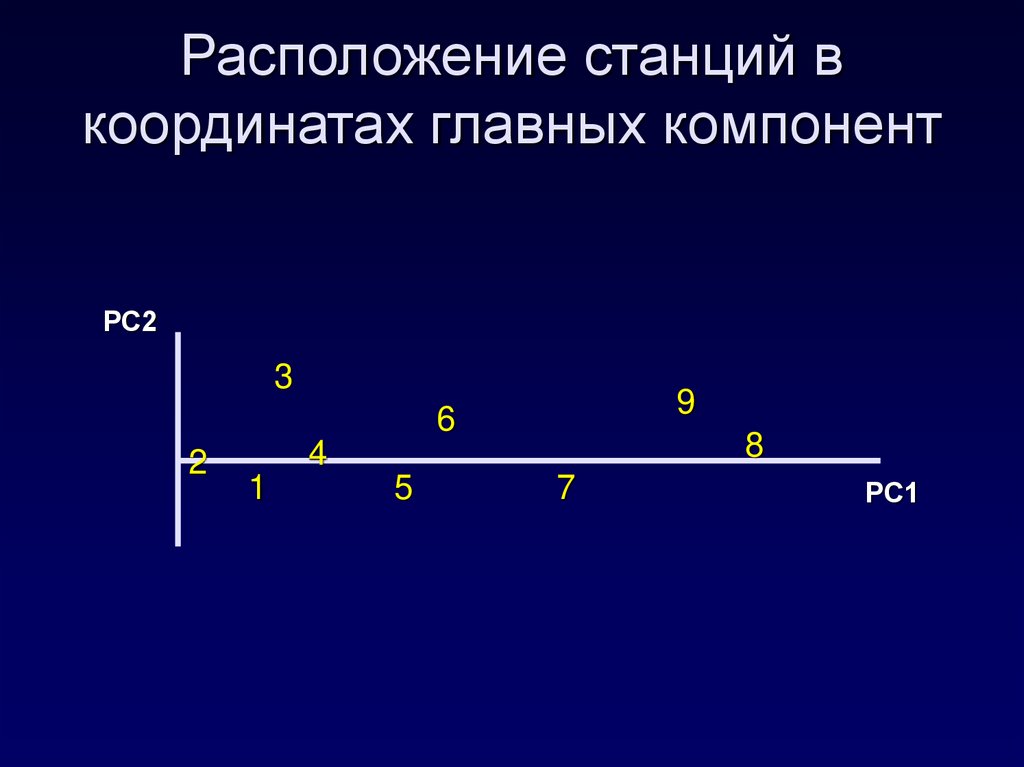
36. Расположение станций в координатах главных компонент
РС23
9
6
2
8
4
1
5
7
РС1
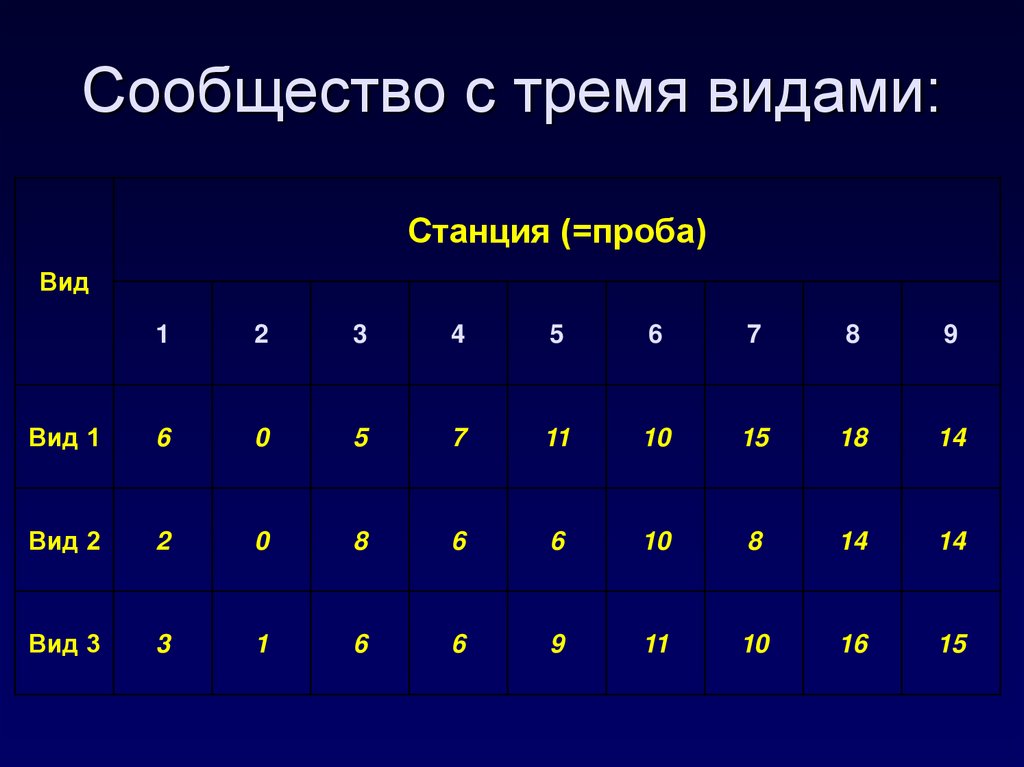
37. Сообщество с тремя видами:
Станция (=проба)Вид
1
2
3
4
5
6
7
8
9
Вид 1
6
0
5
7
11
10
15
18
14
Вид 2
2
0
8
6
6
10
8
14
14
Вид 3
3
1
6
6
9
11
10
16
15
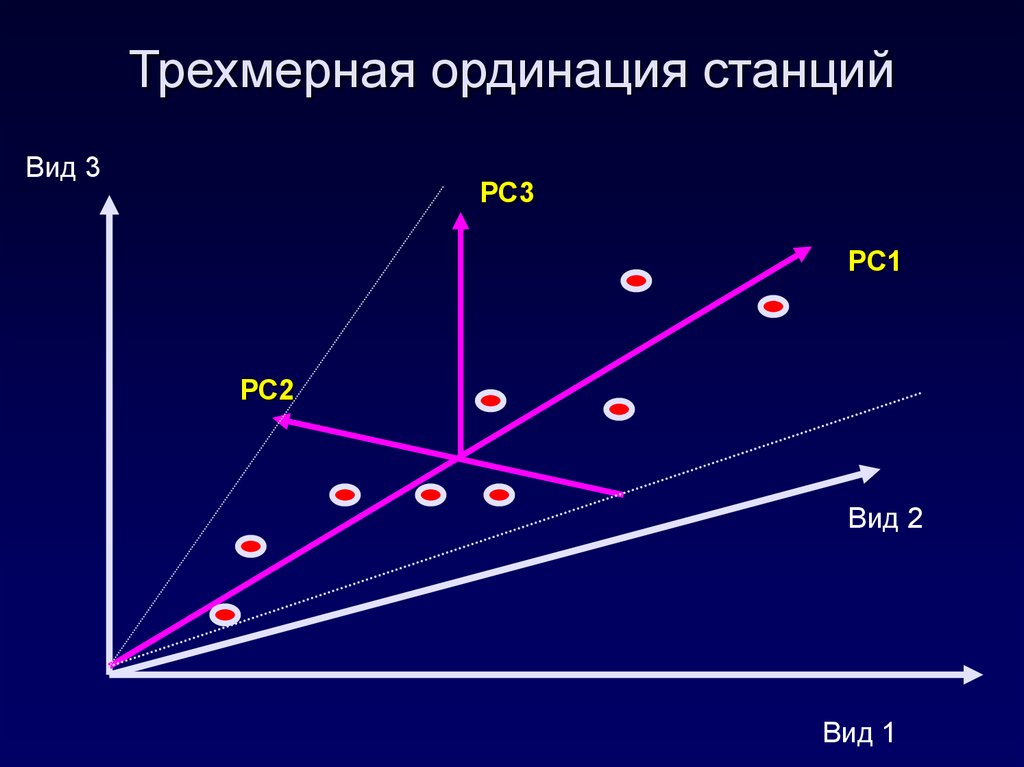
38. Трехмерная ординация станций
Вид 3РС3
РС1
РС2
Вид 2
Вид 1
39. Трехмерная ординация в алгебраическом виде
РС1 = 0.62хВид 1 + 0.52хВид 2 +
0.58Вид 3
РС2 = -0.73хВид 1 + 0.65хВид 2 +
0.20Вид 3
РС3 = 0.28хВид 1 + 0.55хВид 2 0.79Вид 3
40. Важное свойство главных компонент:
var(PC
)
var(
Вид
)
i
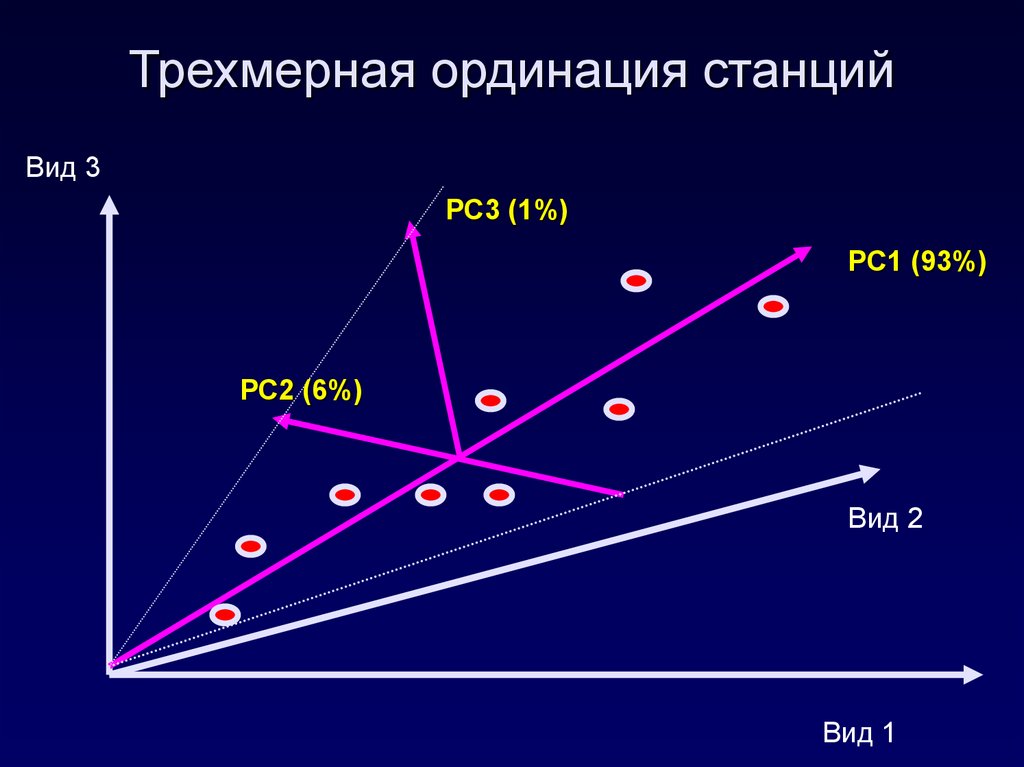
i
41. Трехмерная ординация станций
Вид 3РС3 (1%)
РС1 (93%)
РС2 (6%)
Вид 2
Вид 1
42.
Можно считать, что если главныекомпоненты в сумме объясняют
70-75% дисперсии, то их вполне
достаточно для описания всей
структуры данных.
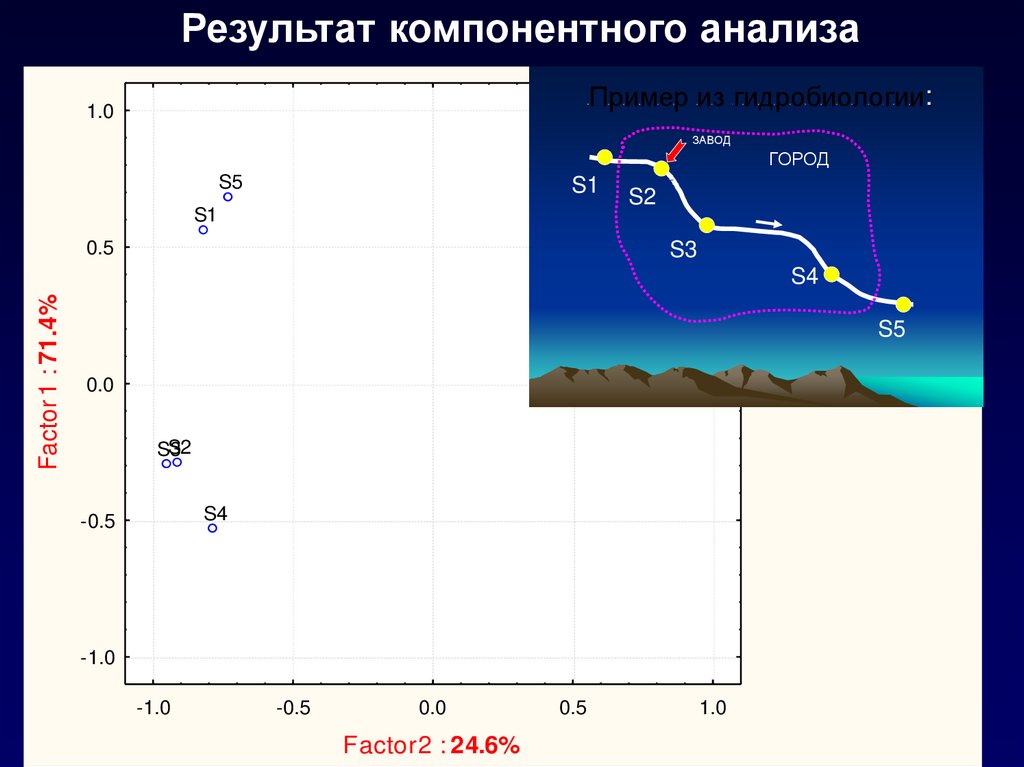
43.
Результат компонентного анализаПример из гидробиологии:
П
1.0
р
и
м
е
р
и
з
г
и
д
р
о
б
и
о
л
о
г
и
ЗАВОД
ГОРОД
S5
S1
S1
0.5
S2
S3
Factor 1 : 71.4%
S4
S5
0.0
S2
S3
S4
-0.5
-1.0
-1.0
-0.5
0.0
Factor 2 : 24.6%
0.5
1.0
и






















 mathematics
mathematics








