Определение машины Тьюринга

1. Определение машины Тьюринга

LOGO

2.

Машина Тьюринга – это строгое
математическое построение,
математический аппарат, созданный для
решения определённых задач.
Машина Тьюринга – абстрактный исполнитель,
осуществляющий алгоритмический процесс, созданный для
уточнения понятия алгоритма.
Это математический объект, а не физическая машина.
Предложена Аланом Тьюрингом в 1936 году

3. Структура и описание машины Тьюринга

Машина Тьюринга состоит из:
бесконечной ленты, разделенной на ячейки;
каретки (читающей и записывающей головки);
программируемого автомата (программа в виде
таблицы).
Автомат каждый раз “видит” только одну ячейку. В зависимости
от того, какую букву он видит, а также в зависимости от своего
состояния q автомат может выполнять следующие действия:
записать новую букву в обозреваемую ячейку;
выполнить сдвиг по ленте на одну ячейку вправо/влево или
остаться неподвижным;
перейти в новое состояние.

4.

Устройство машины Тьюринга
1) Внешний алфавит
А = {a0, a1, …, an}
Элемент a0 называется пустой символ или
пустая буква (признак того, что ячейка пуста).
В этом алфавите в виде слова кодируется исходный набор
данных и результат работы алгоритма.

5.

Устройство машины Тьюринга
2) Внутренний алфавит
Q = {q0, q1, …, qm}, {П, Л, Н!}
В любой момент времени машина Тьюринга находится
в одном из состояний q0, q1, …, qm
При этом:
q1 - начальное состояние (машина
начинает работу)
q0 - заключительное состояние
(машина закончила работу)
Символы {П, Л, Н!} – символы сдвига (вправо, влево,
на месте)

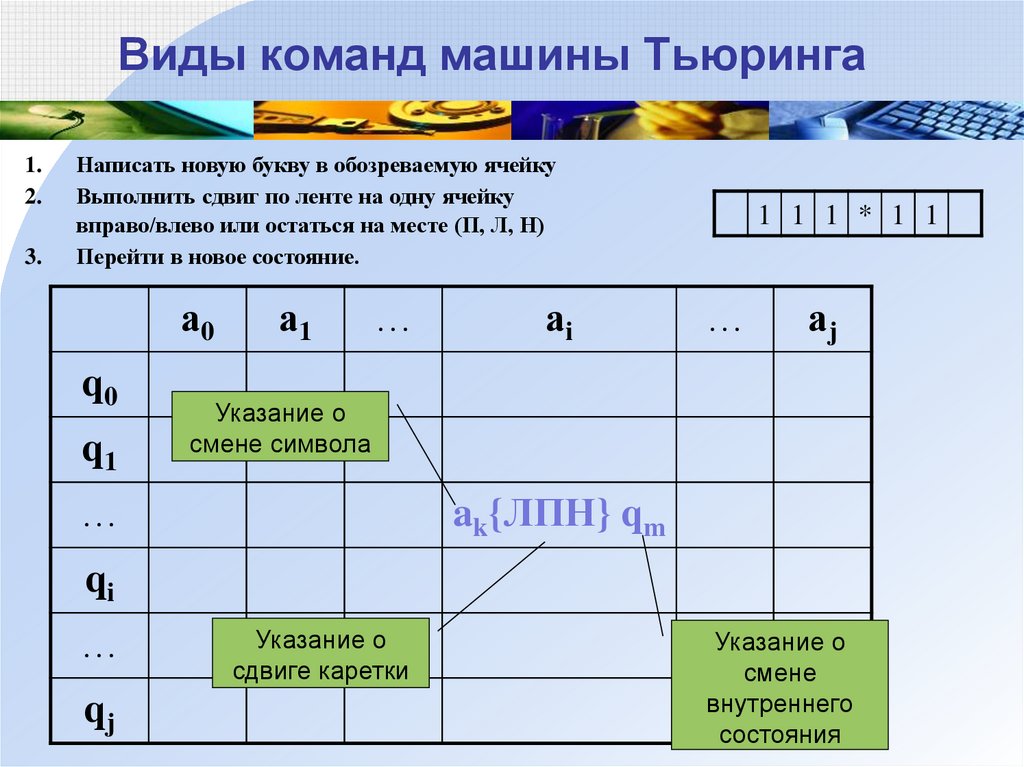
6. Виды команд машины Тьюринга

1.
2.
3.
Написать новую букву в обозреваемую ячейку
Выполнить сдвиг по ленте на одну ячейку
вправо/влево или остаться на месте (П, Л, Н)
Перейти в новое состояние.
а0
q0
q1
а1
…
аi
1 1 1 * 1 1
…
аj
Указание о
смене символа
…
ak{ЛПН} qm
qi
…
qj
Указание о
сдвиге каретки
Указание о
смене
внутреннего
состояния

7.

Устройство машины Тьюринга
3) Внешняя память (лента)
Машина имеет ленту, разбитую на ячейки, в
каждую из которых может быть записана
только одна буква

8.

Устройство машины Тьюринга
3) Внешняя память (лента)
Пустая клетка содержит a0.
В каждый момент времени на ленте
записано конечное число непустых букв
Лента является конечной, но дополняется в любой
момент ячейками слева и справа для записи новых
непустых символов.
Это соответствует принципу абстракции
потенциальной осуществимости

9.

Устройство машины Тьюринга
4) Каретка (управляющая головка)
Каретка машины располагается над
некоторой ячейкой ленты – воспринимает
символ, записанный в ячейке
В одном такте работы каретка сдвигается на
одну ячейку (вправо, влево) или остается на
месте

10.

Устройство машины Тьюринга
5) Функциональная схема (программа)
Программа машины состоит из команд:
Для каждой пары (qi, aj) программа машины
должна содержать одну команду
(детерминированная машина Тьюринга)

11.

Описание работы машины Тьюринга
К началу работы машины на ленту подается
исходный набор данных в виде слова
Будем говорить, что непустое слово в алфавите
А\{a0} воспринимается машиной в стандартном
положении, если:
- оно задано в последовательных ячейках ленты,
- все другие ячейки пусты,
- машина обозревает крайнюю правую ячейку из тех, в
которых записано слово

12.

Описание работы машины Тьюринга
Стандартное положение называется
начальным (заключительным), если
машина, воспринимающая слово в
стандартном положении, находится в
начальном состоянии q1 (стоп-состоянии q0)

13.

Описание работы машины Тьюринга
Находясь в не заключительном состоянии,
машина совершает шаг, который
определяется текущим состоянием qi и
обозреваемым символом aj

14.

Описание работы машины Тьюринга
В соответствии с командой qiaj qkal Х
выполняются следующие действия:
1) Содержимое обозреваемой ячейки aj стирается и
в нее записывается символ al (который может
совпадать с aj)
2) Машина переходит в новое состояние qk (оно
может совпадать с состоянием qi)
3) Каретка перемещается в соответствии с
управляемым символом Х {П, Л, Н!}

15.

Описание работы машины Тьюринга
При переходе машины в заключительное
состояние q0 ее работа прекращается
На ленте записан результат работы
алгоритма – слово в алфавите А\{a0}

16.

Машинным словом (конфигурацией)
машины Тьюринга называется слово вида
1qkal 2, где 1 и 2 - слова в алфавите А.

17.

Конфигурация 1qkal 2 интерпретируется
следующим образом:
- машина находится в состоянии qk
- каретка обозревает на ленте символ al
- 1 и 2 – это содержимое ленты до и после
символа al

18.

Люди могут вести себя по-разному в
одинаковых ситуациях, и этим они
принципиально отличаются от
машин.

19. Машина Поста

LOGO

20.

Машина Поста (МП) – абстрактная
вычислительная машина, предложенная
Эмилем Леоном Постом, которая
отличается от машины Тьюринга большей
простотой.
Обе машины эквиваленты
Эмиль Леон Пост (11.02.1897 (Польша) -21.04.1954) –
американский математик и логик

21.

Машина Поста состоит из каретки
(считывающей и записывающей головки) и
ленты, разбитой на ячейки (лента условно
бесконечна)

22.

Каждая ячейка ленты может быть пустой (0)
или содержать метку (1)

23.

За один такт машина Поста может:
- сдвинуть каретку на одну позицию влево
или вправо
- поставить или стереть метку в ячейке,
обозреваемую машиной
- проверить наличие метки в обозреваемой
ячейке и перейти к команде с заданным
номером

24.

Работа машины Поста определяется
программой, состоящей из конечного числа
строк

25.

Всего шесть команд:
N. , J
- сдвиг вправо
N. , J
- сдвиг влево
N. 1, J
- запись метки
N. 0, J
- удаление метки
N. ?, J1, J0
- если в ячейке метка, то
перейти к команде J1,
если ячейка пуста –
к ячейке J0
N. Stop
- остановка
При этом: N – порядковый номер команды
J – номер следующей команды

26.

Для работы машины Поста нужно задать
программу и ее начальное состояние
(состояние ленты и позицию каретки)

27.

В ходе работы машины Поста может произойти
следующее:
1) Будет выполнена команда Stop и получен результат
работы алгоритма
2) Встречается невыполнимая команда (стирание
несуществующей метки или запись в ячейку с меткой)
3) Машина будет работать бесконечно

28.

Замечание
Определяя машину Поста и машину Тьюринга
авторы пытались задать исполнителя и
алгоритмический процесс как можно проще –
так, чтобы можно было показать несуществование
алгоритма для решения какой-нибудь задачи
Исходя из этого определялись элементы и
принципы работы машин Поста и Тьюринга

29.

Великие силы – только для великих
целей

30. Контрольные вопросы:

1. Зачем понадобилось уточнять понятие «алгоритм»?
2. Какие задачи рассматриваются в теории алгоритмов?
3. Почему можно ограничиться алгоритмами обработки символьных строк? Можно ли
рассматривать только алгоритмы для преобразования двоичных кодов?
4. Как вы понимаете утверждение «Алгоритм задаёт некоторую функцию»?
5. Как связаны понятия «алгоритм» и «исполнитель»?
6. Что такое программа?
7. В каком случае говорят, что два алгоритма эквивалентны?
8. Сравните интуитивное и строгое понятия алгоритма.
9. Опишите устройство и систему программирования машины Тьюринга.
10. Что такое состояние машины Тьюринга?
11. Сопоставьте устройство машины Тьюринга с устройством компьютера. Какие устройства
машины Тьюринга выполняют те же функции, что и аналогичные устройства компьютера?
12. В чем особенность состояний q0 и д, машины Тьюринга?
13. Сформулируйте тезис Чёрча-Тьюринга.
14. Сравните машины Тьюринга и Поста.
15. Зачем нумеруются строки в программе для машины Поста?