Similar presentations:
Общие понятия теории множества
1.
Общие понятиятеории множества
Преподаватель: Е.А. Ковалева
1
2.
Определение:Совокупность элементов, объеденных
некоторым признаком, свойством,
составляет понятие множество.
Например, множество книг в
библиотеке, множество студентов в
группе, множество натуральных чисел
N и т.д.
2
3.
Условия:1.
Должно существовать правило,
позволяющее определить,
принадлежит ли указанный элемент
данной совокупности.
2.
Должно существовать правило,
позволяющее отличать элементы друг
от друга.
(Это, в частности, означает, что множество
не может содержать двух одинаковых
элементов).
3
4.
Множества обычно обозначаютсязаглавными латинскими буквами,
например, А, В, С …, их элементы –
малыми a, b, c...
Если элемент a принадлежит множеству
A, то это обозначается:
Аналогично
читаем как: элемент
a не принадлежит множеству A.
4
5.
Если каждый элемент множества Bявляется также и элементом
множества A, то говорят, что
множество B является
подмножеством множества A:
5
6.
ЗАДАНИЕ МНОЖЕСТВ6
7.
1. Перечисление его элементов:Например, А={2, 6, 15} (множество А
состоит из трѐх элементов – целых
чисел 2, 6, 15).
Но не все множества можно задать
списком (например, множество чисел,
оканчивающихся на 5 бесконечно).
7
8.
2. Указание свойств элементовмножества:
Такая запись читается как: М состоит из
тех (всех) элементов b, которые
обладают признаком Р.
8
9.
3. Порождающая процедура (илиалгоритмический способ):
которая описывает способ получения элементов
нового множества из уже полученных элементов
или из других объектов. Тогда элементами
множества считаются все объекты, которые
могут быть получены с помощью этой
процедуры.
9
10.
Если множество не содержит элементов,обладающим характеристическим признаком, то
оно называется пустым и обозначается
Например, множество целых решений
неравенства
является пустым:
Пустым будет множество действительных решений
уравнений
Множество, не являющееся пустым, называется
непустым.
10
11.
Если элементами множества являютсячисла, то множество называется
числовым.
Непустое множество А называется
конечным, если можно указать такое
фиксированное число
что
количество элементов множества А
меньше n. Множество, не являющееся
ни пустым, ни конечным называется
бесконечным.
11
12.
Универсальным I (единичным)называется множество, в которое входят
все, рассматриваемые множества.
Примеры: если мы говорим о воробьях и
синицах, то универсальным множеством
будет множество птиц; множество планет
Солнечной системы U = {Земля, Марс,
Юпитер, Сатурн, Уран, Меркурий,
Нептун}.
12
13.
ЗАДАНИЕ 1. Что означает запись1) N = {1, 2, 3, …} –
множество натуральных чисел.
2) No={0; 1; 2; 3; ...} - множество
3) Z = {…,-4, -3 -2,- 1, 0, 1, 2, 3, ….} –
4)
13
14.
5)множество М содержит только корни
данного уравнения, т.е. числа
6)
означает, что для любых Х расстояние ОХ меньше или
равно 4, т.е. множество всех точек, для которых
расстояние до Х не больше 4, есть шар с центром в
точке О и радиусом R = 4.
7)
для любых натуральных х, начиная с 7.
14
15.
ИЗОБРАЖЕНИЕМНОЖЕСТВ
15
16.
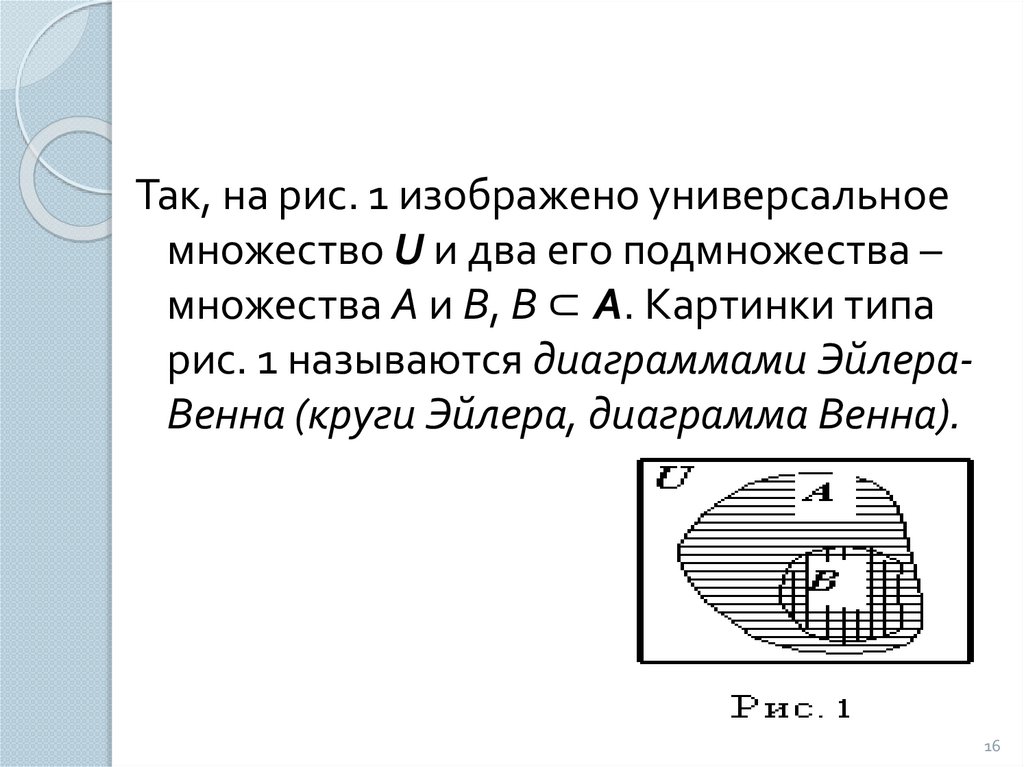
Так, на рис. 1 изображено универсальноемножество U и два его подмножества –
множества А и В, B ⊂ A. Картинки типа
рис. 1 называются диаграммами ЭйлераВенна (круги Эйлера, диаграмма Венна).
16
17.
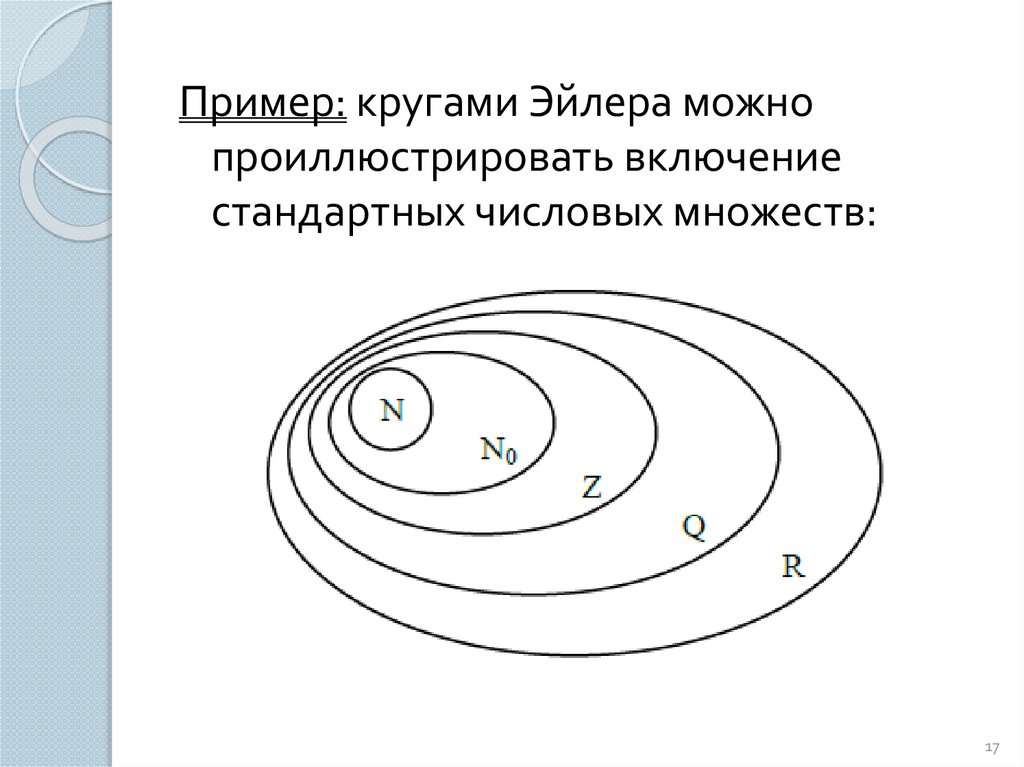
Пример: кругами Эйлера можнопроиллюстрировать включение
стандартных числовых множеств:
17
18.
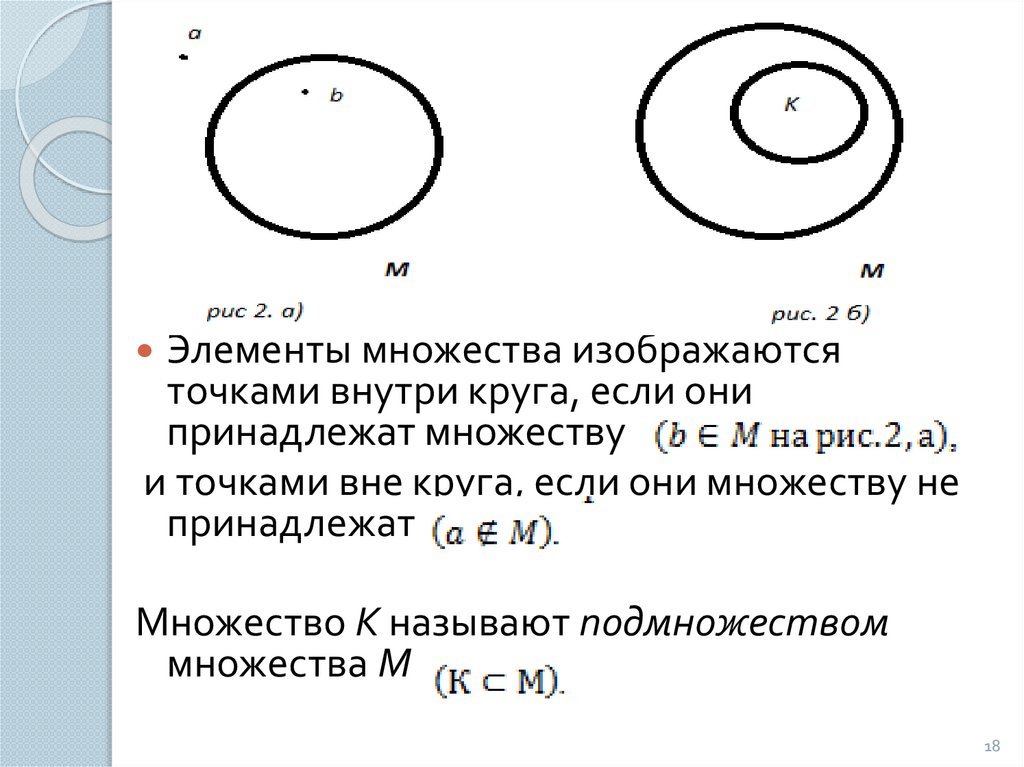
Элементы множества изображаютсяточками внутри круга, если они
принадлежат множеству
и точками вне круга, если они множеству не
принадлежат
Множество К называют подмножеством
множества М
18
19.
Множество К называетсяподмножеством множества М
если для любого
выполняется
Например, добавляя к множеству
однозначных целых чисел
признак «число делится на 3», получаем
множество
19
20.
Для любого непустого множества Мможно сразу указать два его
подмножества независимо от состава и
структуры М: это оно само и пустое.
Очевидно, пустое множество
содержится (является подмножеством)
в любом множестве.
20
21.
Равными называют два множества А и В,состоящие из одинаковых элементов: А = В.
Например, равны множества решений уравнений
так как их решением является одно и тоже число
6.
Равны множество букв, из которых составлены
слова «навес» и «весна».
Равенство двух множеств А и В означает, что
И наоборот, выполнение свойств
означает выполнение равенства A = B.
Эти утверждения равносильны.
21
22.
Число элементов множества А называетсямощностью множества и обозначается
или n(A).
Примеры: 1) мощность пустого множества равна 0:
2) мощность множества планет Солнечной системы
Множества называются равномощными, если их
мощности совпадают.
22
23.
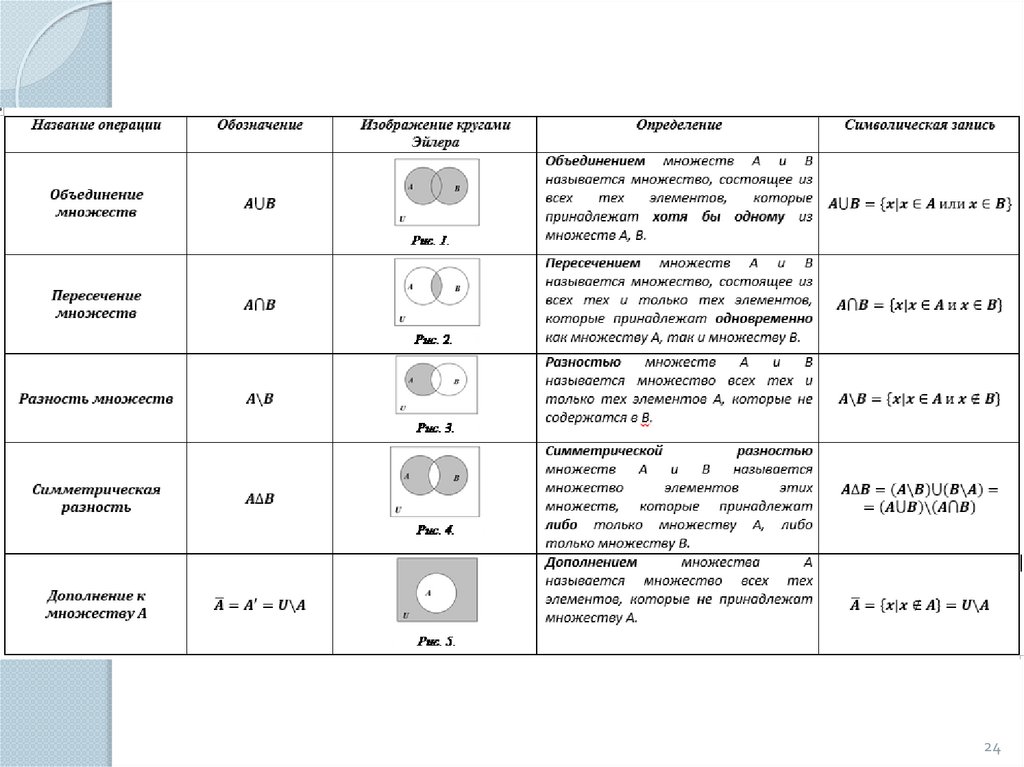
Основные операции надмножествами
Из данных множеств А и В можно построить новые
множества с помощью операций объединения,
пересечения, вычитания и др.
23
24.
2425.
ОТОБРАЖЕНИЯОТОБРАЖЕНИЕ – ОДНО ИЗ ОСНОВНЫХ ПОНЯТИЙ МАТЕМАТИКИ
25
26.
Определение:Отображение есть, какое либо правило
или закон соответствия множеств.
Пусть X и Y – произвольные непустые
множества. Говорят, что задано
отображение f множества X на




























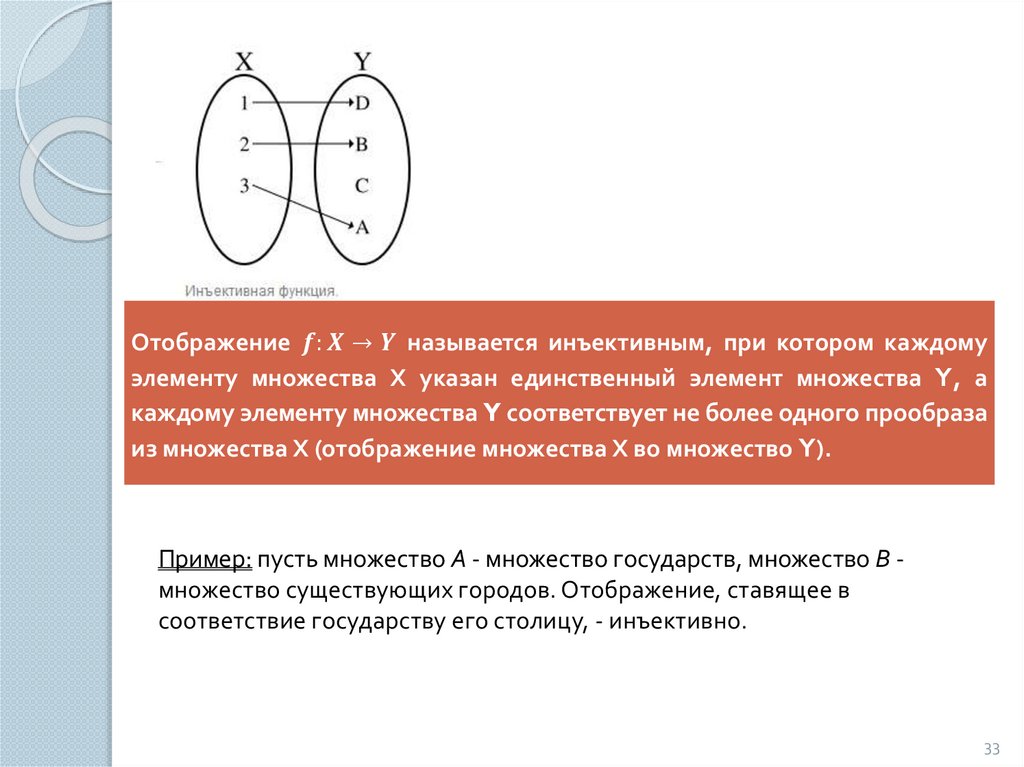
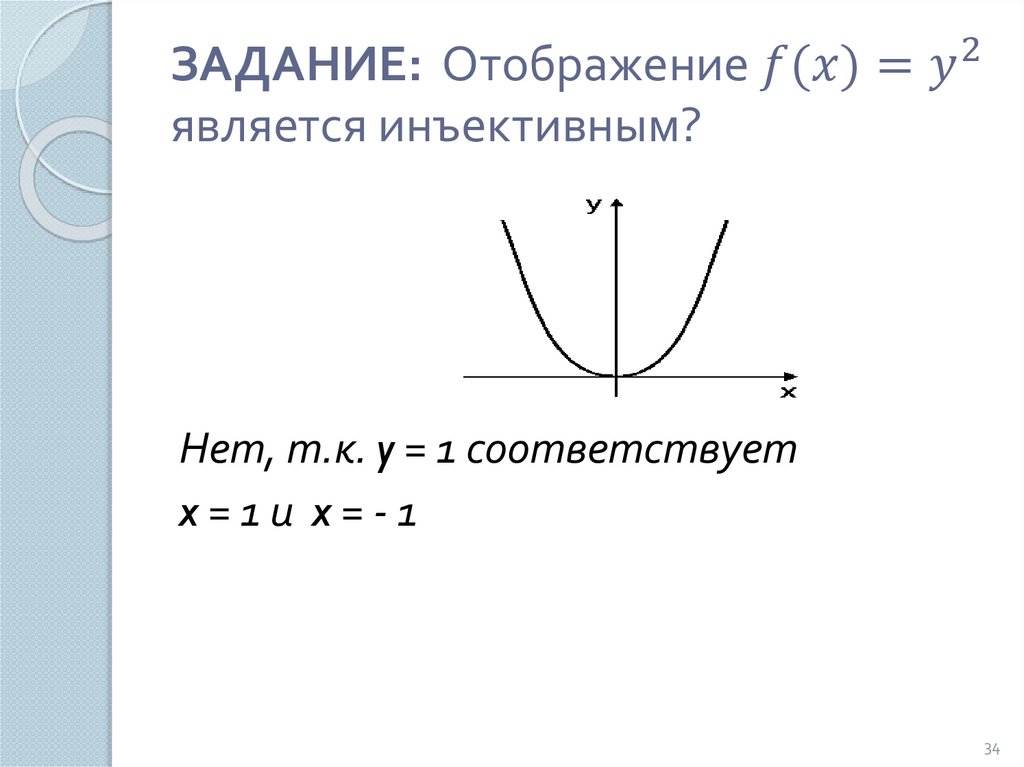

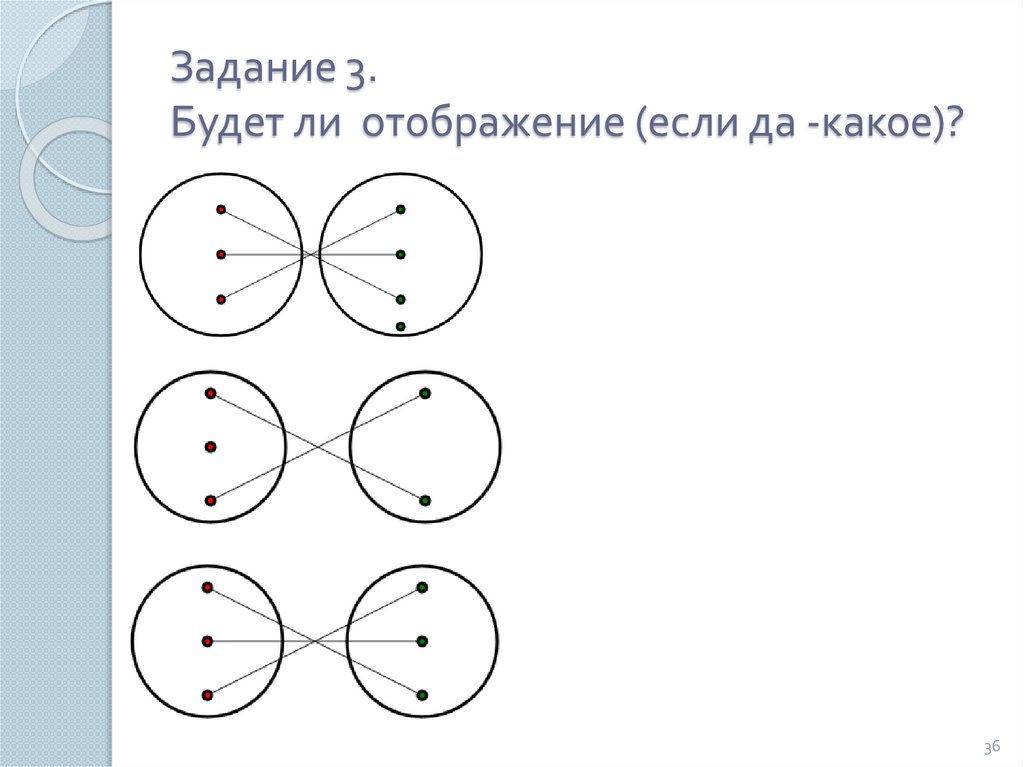

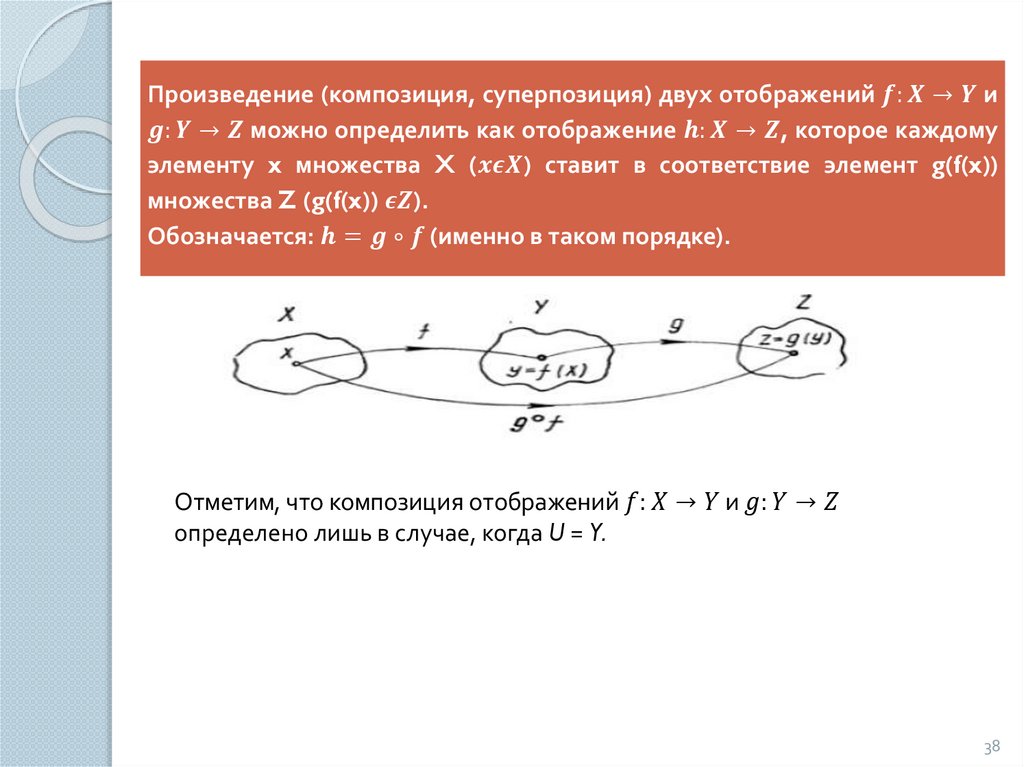






 mathematics
mathematics








