Similar presentations:
Элементы логики в курсе информатики
1. Элементы логики в курсе информатики
2.
греческое logos— слово, мысль, речь, разум
совокупность наук о законах и
формах мышления
3.
Философия(отождествляются законы мышления с
законами бытия)
Ораторское искусство
логические приемы служат не столько
цели достижения истины, сколько
цели убеждения аудитории
4.
IV в. до н.э.Основные работы по логике :
“Первая аналитика” и “Вторая аналитика теория силлогизмов, определение и деление
понятий, теория доказательства;
“Топика” –учение о вероятных “диалектических”
доказательствах;
“Метафизика” - законы правильного мышления:
закон тождества, закон непротиворечия, закон
исключенного третьего
Систематизировал знания по логике и назвал
«формальной»
5.
Традиционная логикиФилософы-стоики: термин «ЛОГИКА»
Средневековые схоласты: изложили
учение Аристотеля в более компактной и
понятной для неподготовленного читателя
форме
6.
ЗАКОН ТОЖДЕСТВА. Всякая мысль тождественна самойсебе, т.е. субъект рассуждений должен быть строго определен и
неизменен до их окончания. Нарушением этого закона является
подмена понятий (часто используется в адвокатской практике).
ЗАКОН НЕПРОТИВОРЕЧИЯ. Два противоположных
суждения не могут быть одновременно истинны: по крайней
мере одно из них ложно.
ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО. Истинно либо
суждение, либо его отрицание ("третьего не дано").
ЗАКОН ДОСТАТОЧНЫХ ОСНОВАНИЙ. Для истинности
всякой мысли должно быть достаточно оснований, т.е.
умозаключение необходимо обосновать исходя из суждений,
истинность которых уже доказана.
7.
ФОРМЫ МЫШЛЕНИЯ:понятие
суждение
умозаключение
8.
Форма мышления, в которойотражаются существенные
отличительные признаки предметов
Две основные логические характеристики:
содержание и объем
9.
совместимые - объемы этих понятий совпадаютполностью или частично
пересечение
тождество
подчинение
несовместимые - объемы которых не совпадают ни в
одном элементе
Соподчинение
противоположность
противоречие
10.
Мысль(выраженная
в
форме
повествовательного
предложения),
в
которой
нечто
утверждается
о
предмете действительности, которая
объективно является либо истинной, либо
ложной
Суждение
истинно (имеет значение
истинности – истина), ЕСЛИ ОНО
СООТВЕТСТВУЕТ ДЕЙСТВИТЕЛЬНОСТИ
11.
Мысль, в ходе которой из одного илинескольких суждений выводится
новое суждение
Посылки - исходные суждения
Заключение - полученное суждение
12.
Если посылки умозаключения истинны,то истинно и заключение.
Если умозаключение справедливо во всех
случаях, то оно справедливо и в каждом
частном случае. (ДЕДУКЦИЯ – переход от
общего к частному)
Если умозаключение справедливо в
некоторых частных случаях, то оно
справедливо во всех случаях. (ИНДУКЦИЯ
– переход от частного к общему.)
13.
Паралогизм – умозаключение,содержащее непреднамеренную ошибку
Софизм – умозаключение, содержащее
преднамеренную ошибку с целью выдать
ложное суждение за истинное.
Парадокс - это умозаключение,
доказывающее как истинность, так и
ложность некоторого суждения
14.
Готфрид ВильгельмЛейбниц
(1646 — 1716)
сделал попытку:
построить
первые
логические
исчисления
заменить простые рассуждения
действиями со знаками и привел
соответствующие правила
15.
Джордж Буль(1815 — 1864)
Перенес на логику законы и правила
алгебраических действий,
Ввёл логические операции,
Предложил способ записи
высказываний в символической форме
Алгебра логики (логика высказываний) — один из основных
разделов математической логики, в котором методы алгебры
используются в логических преобразованиях высказываний.
16.
Высказывание —предложение какоголибо языка (естественного илиискусственного), относительно которого
можно сказать, истинно оно или ложно.
Обозначение: А, В, С , …
Виды: простые, сложные
Истинное высказывание: 1
Ложное высказывание: 0
17.
inversio - лат. Переворачиваюобозначается : не А ; А ; А; NOT A
Образуется из простого высказывания с
помощью добавления частицы "НЕ" к
сказуемому или использованием оборота речи
"НЕВЕРНО, ЧТО ...".
не А
А
18.
conjunctio - лат. Связываюобозначается : А В ; А & В; А * В; А и
В; А AND В; А
Образуется соединением двух
высказываний в одно с помощью союза "И"
19.
disjunctio - лат. РазличаюОбозначается : А или В; А OR В; А V В; А
В
Образуется соединением двух
высказываний в одно с помощью союза
«ИЛИ» (в объединительном смысле)
20.
Обозначается : либо А, либо В; А В;АVВ
Образуется соединением двух
высказываний в одно с помощью слов
либо…, либо…
21.
implicatio - лат. тесно связываюОбозначается : А В;
Читается: "если А, то В"; "из А следует В";
"А имплицирует В"; "А достаточно для В";
"В необходимо для А"; "А только тогда,
когда В"; "В тогда, когда А"
22.
aequivalens - фр. РавноценноеОбозначается : А В; А В
Cоответствует обороту «тогда и только
тогда, когда…», «A необходимо и
достаточно для В»
23.
инверсияконъюнкция
дизъюнкция
импликация и эквивалентность
24.
Логические функции, истинные на всехнаборах значений входных переменных,
называются тождественно-истинными.
Логические функции, ложные на всех наборах
значений входных переменных, называются
тождественно-ложными.
Если у двух логических функций совпадают
таблицы истинности, то есть на всех наборах
значений входных переменных они
принимают одинаковое значение, то их
называют равносильными или
эквивалентными
25.
Построив таблицу истинности для правойи левой части закона;
Выполнив эквивалентные преобразования
над правой и левой частью формулы для
приведения их к одному виду;
С помощью диаграмм Эйлера-Венна;
Путем правильных логических
рассуждений.
26.
Минимизация функции - заменалогической функции более простой, но
равносильной ей функцией:
не содержит операций импликации и
эквиваленции,
содержит по сравнению с исходной меньшее
число операций конъюнкции и дизъюнкции
не содержит отрицаний неэлементарных
формул,
содержит меньшее число вхождений
переменных.
27.
Элементарной конъюнкцией / дизъюнкциейназывается конъюнкция/ дизъюнкция нескольких
переменных, взятых с отрицанием или без отрицания,
причём среди переменных могут быть одинаковые
Всякую дизъюнкцию/конъюнкцию элементарных
конъюнкций / дизъюнкций назовём ДНФ / КНФ
Совершенной ДНФ / КНФ называется ДНФ / КНФ , в
которой нет равных элементарных конъюнкций/
дизъюнкций и все они содержат одни и те же
переменные, причём каждую переменную только один
раз (возможно с отрицанием)
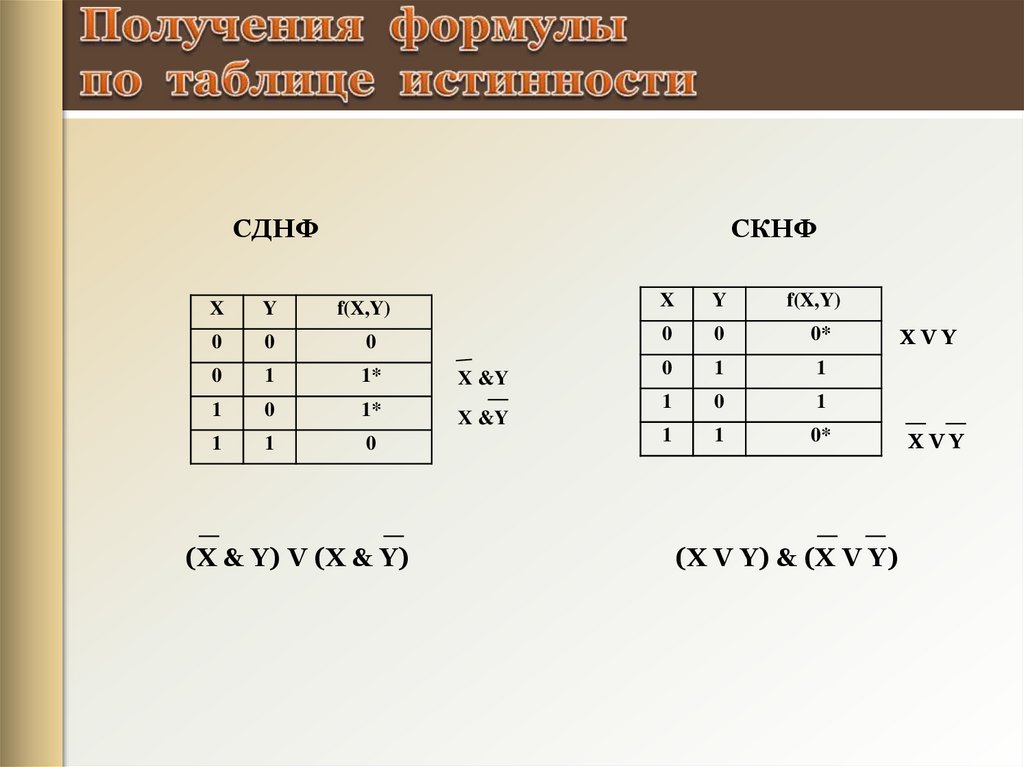
28.
СДНФСКНФ
X
Y
f(X,Y)
X
Y
f(X,Y)
0
0
0
0
0
0*
0
1
1*
X &Y
0
1
1
1
0
1*
X &Y
1
0
1
1
1
0
1
1
0*
(X & Y) V (X & Y)
(X V Y) & (X V Y)
XVY
XVY
29.
Средствами алгебры логикиТабличный
С помощью рассуждений
С помощью диаграмм Венна
С помощью графов
30.
изучается условие задачи;вводится система обозначений для логических
высказываний;
конструируется логическая формула,
описывающая логические связи между всеми
высказываниями условия задачи;
определяются значения истинности этой
логической формулы;
из полученных значений истинности формулы
определяются значения истинности введённых
логических высказываний, на основании которых
делается заключение о решении.
31.
Логический элемент — это схема,реализующая логические операции
дизъюнкции, конъюнкции и инверсии
32.
От английского слова trigger — защёлка, спусковойкрючок
Это электронная схема, широко применяемая в
регистрах компьютера для надёжного запоминания
одного разряда двоичного кода.
S
R
Q
неQ
0
0
запрещено
0
1
1
0
1
0
0
1
1
1
хранение бита
33.
Это электронная логическая схема,выполняющая суммирование двоичных
чисел
Входы
Выходы
Первое
слагаемое
Второе
слагаемое
Перенос
Сумма
Перенос
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
































 informatics
informatics