Similar presentations:
Арифметичні основи функціонування цифрової техніки (тема 2)
1.
Національний аерокосмічний університет ім. М.Є. ЖуковськогоЦифрові пристрої
Digital devices
&
Microprocessors
Мікропроцесори
Тема 2:
Арифметичні основи функціонування
цифрової техніки
к.т.н., доцент каф.501
Мазуренко О.В.
2.
Систем числення. Представлення чиселНайменування
системи числення
Основа системи
числення
Символи (цифри) системи числення
десяткова
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
двійкова
2
0, 1
вісімкова
8
0, 1, 2, 3, 4, 5, 6, 7
шістнадцяткова
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
1
Представлення (подання) числа:
X( q ) ( ) xk 1xk 2 xk 3 ...x1x0 , x 1x 2 x 3 ...x m
Десяткове значення числа:
xk 1 q k 1 xk 2 q k 2 ... x1 q1 x0 q 0 x 1 q 1 x 2 q 2 ... x m q m X ( 10 )
Найбільше за модулем десяткове число
X( 10 ) q k q m
© Мазуренко О.В., 2018
Мікропроцесори і їх програмування
3.
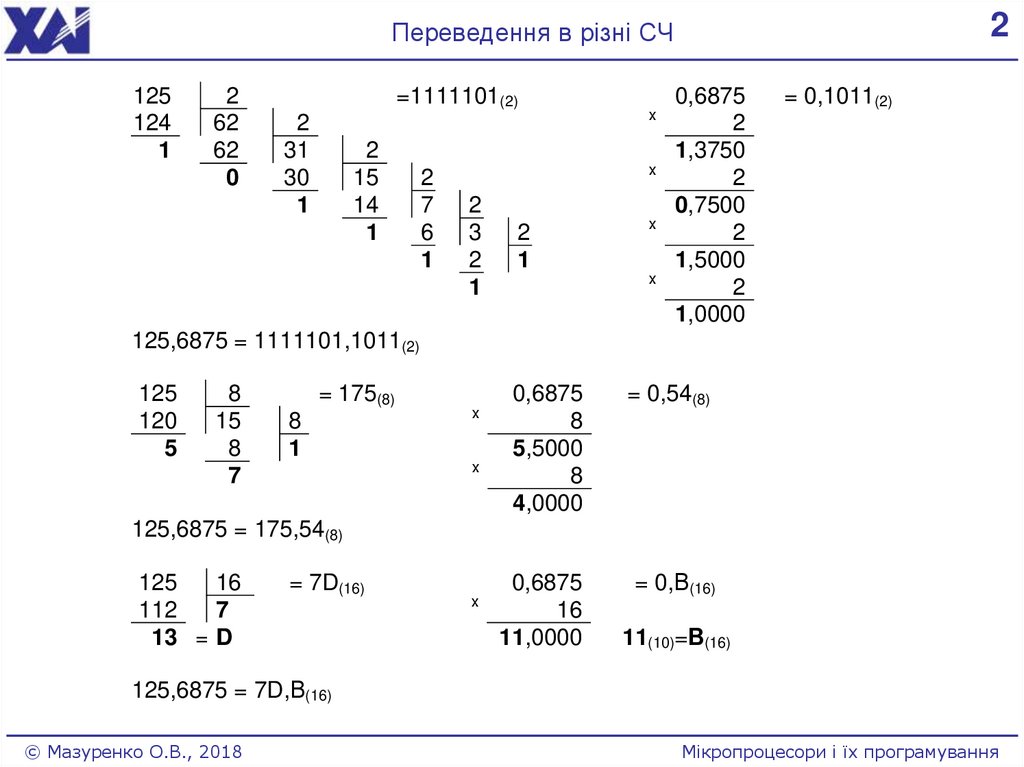
2Переведення в різні СЧ
125
124
1
2
62
62
0
=1111101(2)
2
31
30
1
2
15
14
1
2
7
6
1
х
х
2
3
2
1
2
1
х
х
0,6875
2
1,3750
2
0,7500
2
1,5000
2
1,0000
= 0,1011(2)
125,6875 = 1111101,1011(2)
125
120
5
8
15
8
7
= 175(8)
8
1
х
х
0,6875
8
5,5000
8
4,0000
= 0,54(8)
0,6875
16
11,0000
= 0,В(16)
125,6875 = 175,54(8)
125
16
112
7
13 = D
= 7D(16)
х
11(10)=В(16)
125,6875 = 7D,В(16)
© Мазуренко О.В., 2018
Мікропроцесори і їх програмування
4.
3Переведення в різні СЧ
3
2
7
,
6
4
011
010
111
,
110
100
= 11010111,1101 (2)
(8)
001
010
101
,
011
100
1
2
5
,
3
4
5
F
,
1
A
0101
1111
,
0001
1010
0011
0010
1011
,
0101
1100
3
2
11(В)
,
5
12(С)
© Мазуренко О.В., 2018
(16)
(2)
= 125,34 (8)
= 1011111,0001101 (2)
(2)
= 32В,5С (16)
Мікропроцесори і їх програмування
5.
Правила арифметичних операцій в двійковій СЧПравила додавання:
Правила віднімання:
0+0=0
0+1=1
1+0=1
1 + 1 = 10
0-0=0
1-0=1
1-1=0
10 - 1 = 1
4
Правила множення:
0*0=0
0*1=0
1*0=0
1*1=1
© Мазуренко О.В., 2018
Мікропроцесори і їх програмування
6.
Коди представлення чисел5
Прямий код числа:
0 хk 1 хk 2 ... х1 х0 , х 1 х 2 ...х m 1 х m , X 0
X пр
1 хk 1 хk 2 ... х1 х0 , х 1 х 2 ...х m 1 х m , X 0
Зворотний код числа:
X 0
0 хk 1 хk 2 ... х1 х0 , х 1 х 2 ...х m 1 х m ,
X зв
1 x k 1 x k 2 ... x1 x 0 , x 1 x 2 ...x m 1 x m , X 0
Приклад:
Задана розрядна сітка k=3, m=4, записати
зворотні коди чисел:
X=+101,1010 → Xзв=0010,0101
X= -101,1010 → Xзв=1010,0101
© Мазуренко О.В., 2018
Мікропроцесори і їх програмування
7.
6Коди представлення чисел
Додатковий код числа:
X 0
0 хk 1 хk 2 ... х1 х0 , х 1 х 2 ...х m 1 х m ,
X дод
m
1 x k 1 x k 2 ... x1 x 0 , x 1 x 2 ...x m 1 x m 2 , X 0
Приклад:
X=+101,1010 → 0010,0101 →
0010,0101
+
© Мазуренко О.В., 2018
1
0010,0110
Мікропроцесори і їх програмування
8.
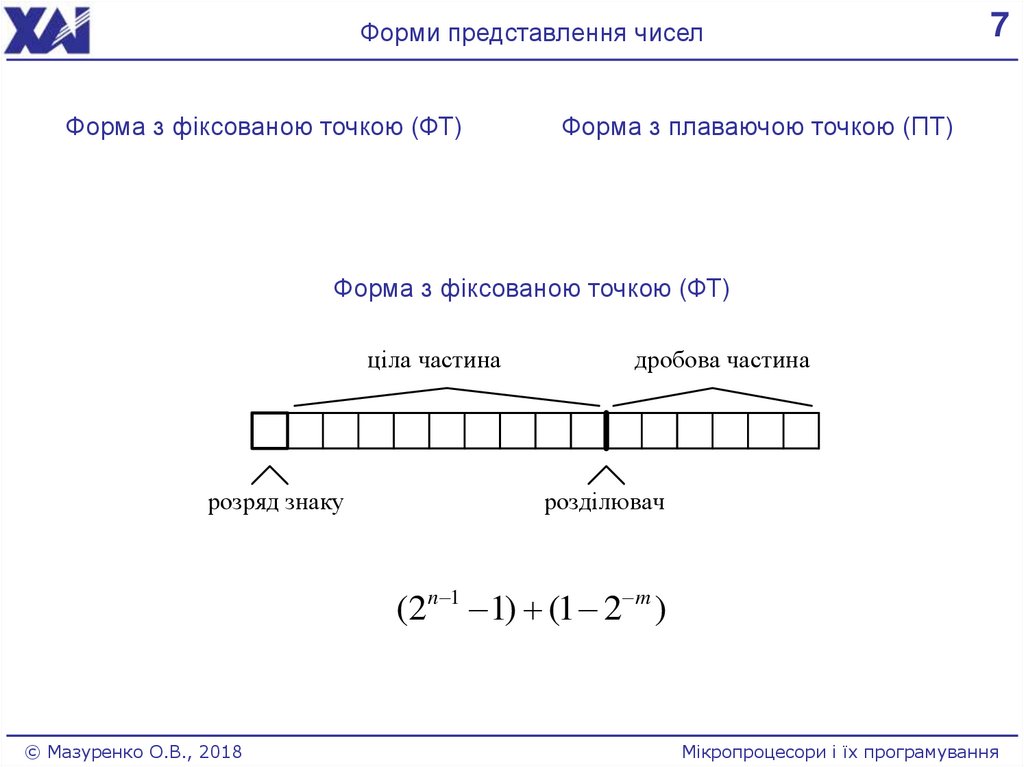
Форми представлення чиселФорма з фіксованою точкою (ФТ)
7
Форма з плаваючою точкою (ПТ)
Форма з фіксованою точкою (ФТ)
ціла частина
розряд знаку
дробова частина
розділювач
(2n 1 1) (1 2 m )
© Мазуренко О.В., 2018
Мікропроцесори і їх програмування
9.
Форми представлення чисел8
Форма з плаваючою точкою (ПТ)
N M 2P
де М – мантиса числа; P – порядок числа.
мантиса (М)
знак М
порядок (Р)
знак Р
Нормалізоване представлення:
0,5 M 1
© Мазуренко О.В., 2018
Мікропроцесори і їх програмування






 mathematics
mathematics informatics
informatics








