Similar presentations:
Сигналы, обеспечивающие повышенную помехозащищенность и скрытность телекоммуникационных систем
1.
кафедра информационнотелекоммуникационных систем и технологийДисциплина Анализ информационной
безопасности телекоммуникационных систем
Тема 4 Сигналы, обеспечивающие повышенную
помехозащищенность и скрытность
телекоммуникационных систем
профессор
Белов Сергей Павлович
1
2.
ЦЕЛЬЮ темы является - изучение особенностей формированияузкополосных и широкополосных сигналов. Особое внимание
при
рассмотрении
узкополосных
сигналов
уделено
сигнально-кодовым
конструкциям,
имеющим
высокую
спектральную
эффективность.
При
рассмотрении
широкополосных сигналов основное внимание уделено
сигналам, полученным на основе применения специальных
кодов и новых методов расширения спектра.
ЗАДАЧИ лекции:
1 изучение особенностей
сигналов
формирования
широкополосных
Литература
1. Белов, С.П., Жиляков, Е.Г. Анализ информационной безопасности
телекоммуникационных
систем:
Учебно-методический
комплекс. : http://pegas.bsu.edu.ru/course/view.php?id=8360
Белгород, 2015 год.
3.
Известен ряд методов получения сложных сигналов, которые ужедлительное время широко используются при передаче информации в
инфокоммуникационных системах различного назначения. В их основе
лежит использование псевдослучайных бинарных последовательностей
или частотно-временного кодирования. Достоинством этих методов состоит
в том, что они могут быть реализованы с применением типовых элементов и
устройств цифровой техники. Однако в настоящее время в связи с
очевидным прогрессом в области построения быстродействующих
цифровых
элементов,
стало
возможным
формирование
с
их
использованием сложных сигналов с линейной частотной модуляцией и
других классов широкополосных сигнально-кодовых конструкций.
Рассмотрим особенности формирования некоторых из существующих
классов широкополосных сигналов и проанализируем, с учетом специфики
читаемой дисциплины, их частотные и корреляционные характеристики.
4.
Формирование сложных сигналов с помощью псевдослучайных бинарныхпоследовательностей
Псевдослучайной бинарной последовательностью длительностью τ0 называют
последовательность, сформированную по определенным правилам из дискретных
элементов 0 и 1 так, чтобы ее корреляционные свойства были близки к
соответствующим свойствам шумовой реализации такой же длительности. Если
обозначить длительность элемента последовательности через τ0, то число таких
элементов в последовательности с длительностью τ0 будет равно
(1)
Такие последовательности в литературе часто называют М - последовательностями, а
величину М - длиной последовательности. Наиболее известны и хорошо исследованы М
- последовательности, формируемые (генерируемые) двоичным регистром сдвига с
логической обратной связью. Такой регистр представляет собой m последовательно
соединенных триггерных ячеек, управляемых периодической последовательностью
тактовых импульсов, вырабатываемых тактовым генератором, и импульсами,
формируемыми в устройстве логической обратной связи. Упрощенная структурная
схема регистра показана на рисунке. Ключи К1 и К2 в схеме введены условно
и нужны лишь для пояснения ее работы.
Рассмотрим работу этой схемы. Каждое плечо
триггера (Т) может принимать два состояния —
закрытое и открытое (которое можно условно
обозначать символами 0 и 1 или наоборот).
Состоянием триггера будем называть состояние
одного из его плеч (например, левого).
Обозначим начальное состояние триггеров
регистра через γ01,…,γ02,…,γ0j,…,γ0m.
5.
Ключи К1 и К2 при этом считаем разомкнутыми. Пусть в момент t0 ключ К1замыкается и на все триггерные ячейки начинают поступать импульсы от генератора
тактовых импульсов (ГТИ). Под действием этих импульсов триггеры изменяют свое
состояние на противоположное или сохраняют прежнее состояние в зависимости от
того, какое начальное состояние имел данный триггер и триггер, находящийся перед
ним. В результате каждый триггер последовательно принимает все состояния
предшествующих ему триггеров. Если снимать напряжение с последнего триггера, то
оно последовательно принимает состояния γ0m,…,γ0(m-1),…,γ0j,…,γ01, т. е.
представляет
собой
последовательность,
состоящую
из
m
элементов,
соответствующих символам 0 и 1. После m тактовых импульсов напряжение на выходе
последней триггерной ячейки не меняется и она принимает состояние γ01.
Таким образом, если регистр не имеет обратной связи (ключ К2 разомкнут), то под
действием тактовых импульсов на его выходе образуется только одна кодовая
комбинация из m элементов, соответствующих начальным состояниям триггерных
ячеек. В данном случае регистр представляет собой устройство памяти, в котором
«записана» некоторая кодовая комбинация, которая может быть выведена (считана) в
нужное время. Чтобы регистр формировал дискретную последовательность
непрерывно, т.е. работал как генератор такой последовательности, необходимо ввести
обратную связь – замкнуть ключ К2. В этом случае в устройстве логической обратной
m
связи формируется функция
(2)
Fл ( 1 , 2 ,..., j ,..., m ) b j j (mod 2)
j 1
которая называется логической функцией обратной связи. В (2) коэффициенты bj могут
принимать значения 1 или 0 в зависимости от того, какие ячейки триггеров участвуют в
формировании функции Fл, определяющей обратную связь. Значения yj определяются
фактическими состояниями триггерных ячеек в процессе работы.
6.
Получение логической функции сводится к выбору совокупности коэффициентов bj,определяющих, какие ячейки триггеров должны быть связаны с устройством логической
обратной связи. Коэффициенты bj выбираются в соответствии с определенным
правилом, которое позволяет получить последовательность максимальной длины для
регистра с заданным числом ячеек. Это правило может быть установлено на основе
хорошо разработанной теории рекуррентных последовательностей. Сформированная в
соответствии с логической функцией последовательность символов 0 и 1 подается на
вход первой триггерной ячейки регистра. В результате действия тактовых импульсов и
импульсов обратной связи регистр окажется в режиме непрерывной смены состояний,
т. е. будет генерировать дискретную последовательность элементов. Общее число
различных состояний, которые последовательно примет регистр сдвига, определяется
числом триггерных ячеек m, каждая из них может находиться в одном из двух возможных
состояний. Очевидно, что число различных состояний регистра, (исключая нулевое
состояние) равно
(3)
M 2m 1
Следовательно, после каждых М разных состояний регистр, находящийся в режиме
генерирования, начинает повторять эти состояния. Иными словами, регистр генерирует
дискретную последовательность элементов, структура которой периодически
повторяется, через каждые М элементов. Величина М поэтому называется периодом
последовательности. Регистр с обратной связью, образованный суммированием по
«модулю два» состояний некоторых заранее выбранных триггерных ячеек, называется
линейным регистром сдвига или генератором псевдослучайной последовательности
импульсов. Генерируемую последовательность можно снимать не только с выхода
последнего триггера, но и с любого другого триггера. При этом последовательность
имеет ту же структуру и отличается только сдвигом по времени.
7.
Проведенное рассмотрение показывает, что линейный регистр сдвига преобразуетинформационную
последовательность
простых
двоичных
символов
в
последовательность сложных двоичных символов. При этом каждому простому
информационному символу 0 или 1 однозначно соответствует сложный символ 0 или
1, представляющий собой определенную комбинацию из М двоичных элементов. Если
правило ввода начальных условий изменить (например, поменять некоторые плечи
триггеров, на которые задаются начальные условия; не подавать начальные условия
на некоторые триггеры и т. п.), то исходным символам 0 и 1 станут соответствовать
сложные символы 0 и 1 с другой внутренней структурой. Нетрудно видеть, что в
зависимости от задаваемых начальных условий одну и ту же исходную
информационную последовательность простых двоичных символов регистр сдвига
будет преобразовывать в последовательность с различными сложными двоичными
символами. Так как в зависимости от начальных условий регистр сдвига может
принимать М различных состояний, то, очевидно, каждому простому символу 0 или 1
можно поставить в соответствие один из М сложных символов 0 или 1. Эта
особенность работы регистра сдвига открывает ряд возможностей для решения
различных прикладных задач. Многочисленные исследования показали, что свойства
М-последовательностей близки к свойствам случайных последовательностей.
Причем, чем больше длина периода М, тем ближе это сходство. Поскольку, однако,
природа М-последовательностей не случайна и они могут быть воспроизведены
многократно, их называют псевдослучайными последовательностями. Если
полученную последовательность сложных информационных символов подать на
модулятор и выполнить манипуляцию одного из параметров несущего колебания, то в
результате образуется сложный сигнал, свойства и структура которого полностью
определяется свойствами поданной последовательности и видом выбранной
манипуляции. Наибольшее распространение в настоящее время получили сложные
сигналы, образованные манипуляцией начальной фазы несущей.
8.
В математической записи псевдослучайный сигнал с фазовой манипуляцией (ПСП ФМ)имеет следующий вид:
T Э
t
l
1
N
Э
2 2 exp j t ;
S 0 l rect
0
S t
l 1
Э
0; при других t
при t
T
2
(4)
где S0 - амплитуда огибающей сигнала, в дальнейшем постоянная величина, равная 1,
τэ - длительность элемента кодирующей последовательности; N-количество элементов
в кодирующей последовательности; l- коэффициент, характеризующий состояние
кодирующей последовательности, принимает значения +1 или -1, Т- длительность
сигнала;rect(x) – прямоугольная «срезающая» функция, задаваемая выражением:
1
1
,
при
х
;
2
rect ( x)
0, при х 1 .
2
Рисунок 2
Временная диаграмма
рассматриваемых сигналов
9.
ПСП ФМ сигналы, как и большинство других классов ШШКС не являютсяортогональными при произвольном временном и частотном сдвиге, в этом случае можно
говорить только о квазиортогональности этих сигналов, то есть о приближении сложных
сигналов к классу ортогональных. Для оценки степени ортогональности сигналов при их
временном и частотном смещении используют функцию неопределенности (ФН), которая
в математической форме может быть записана следующим образом:
.
.
1
, Fд
S t S t exp j 2 Fдt dt
2 E
.
F
где: τ - временной сдвиг между сигналами, д
a
* f0
c
- допплеровский
сдвиг частоты,
.
*
Е – энергия сигнала,
- огибающая принимаемого сигнала, S j t - комплексносопряженная огибающая сигнала
Рисунок 3. ФН ПСП ФМ сигнала, M=31
Рисунок 4. ФН ПСП ФМ сигнала, M=127
10.
Рисунок 5. Частотный спектр ПСП ФМ сигнала, M=31Рисунок 6. Частотный спектр
ПСП ФМ сигнала, M=127
Из приведенных рисунков 3-6 видно:
1) значения уровней боковых лепестков ФН ПСП ФМ сигналов уменьшаются с
увеличением М, хотя их величина значительно выше, чем у кода Баркера;
2) даже при незначительной величине доплеровского сдвига по частоте значение
главного лепестка ФН существенно уменьшается;
3) распределение энергетических составляющих энергетического спектра ФН ПСП ФМ
сигналов неравномерно.
Таким образом ФН ПСП ФМ сигналы не обладают свойством инвариантности к
доплеровскому рассогласованию по частоте, они также не обеспечивают минимума
затрат частотно-временных ресурсов инфокоммуникационных систем из-за высокой
неравномерности распределения энергетических составляющих в частотной области.
11.
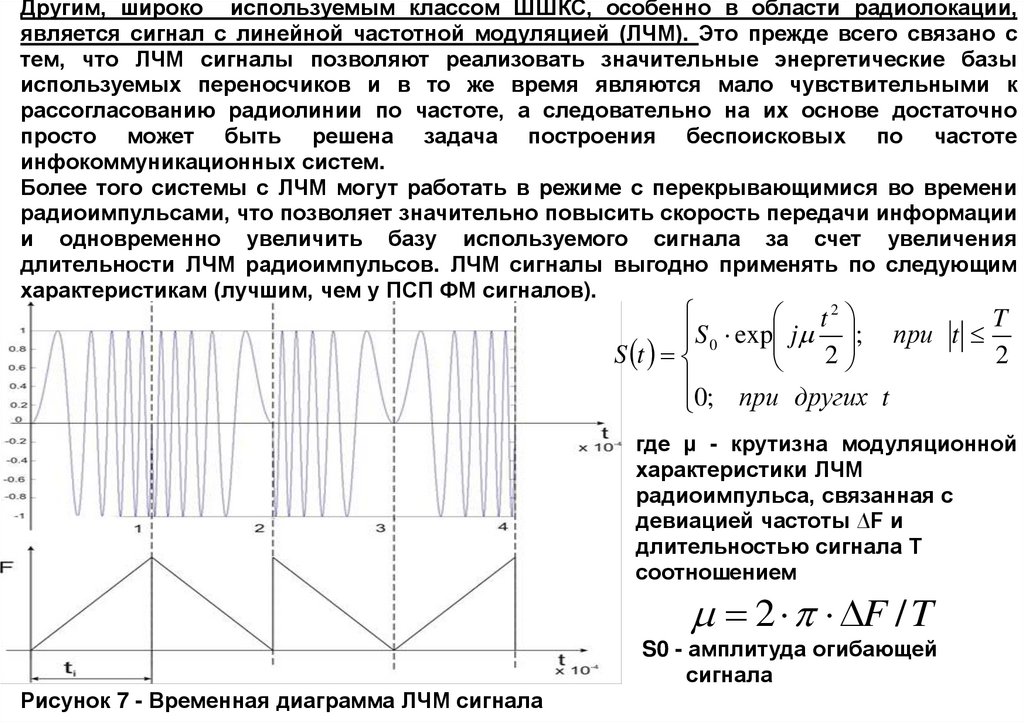
Другим, широко используемым классом ШШКС, особенно в области радиолокации,является сигнал с линейной частотной модуляцией (ЛЧМ). Это прежде всего связано с
тем, что ЛЧМ сигналы позволяют реализовать значительные энергетические базы
используемых переносчиков и в то же время являются мало чувствительными к
рассогласованию радиолинии по частоте, а следовательно на их основе достаточно
просто может быть решена задача построения беспоисковых по частоте
инфокоммуникационных систем.
Более того системы с ЛЧМ могут работать в режиме с перекрывающимися во времени
радиоимпульсами, что позволяет значительно повысить скорость передачи информации
и одновременно увеличить базу используемого сигнала за счет увеличения
длительности ЛЧМ радиоимпульсов. ЛЧМ сигналы выгодно применять по следующим
характеристикам (лучшим, чем у ПСП ФМ сигналов).
t2
T
S
exp
j
;
при
t
S t 0
2
2
0; при других t
где μ - крутизна модуляционной
характеристики ЛЧМ
радиоимпульса, связанная с
девиацией частоты ∆F и
длительностью сигнала Т
соотношением
2 F / T
S0 - амплитуда огибающей
сигнала
Рисунок 7 - Временная диаграмма ЛЧМ сигнала
12.
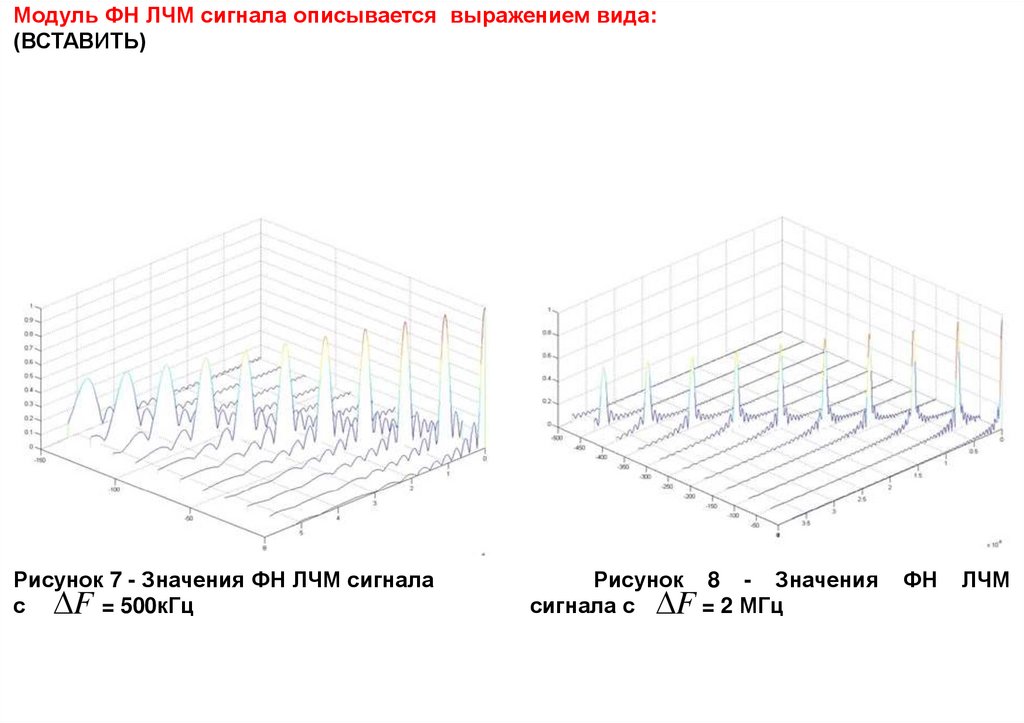
Модуль ФН ЛЧМ сигнала описывается выражением вида:(ВСТАВИТЬ)
Рисунок 7 - Значения ФН ЛЧМ сигнала
с F = 500кГц
Рисунок 8 - Значения
сигнала с F = 2 МГц
ФН
ЛЧМ
13.
Рисунок 9 – Частотный спектрРисунок 10 – Частотный спектр
ЛЧМ сигнала с F = 500кГц
ЛЧМ сигнала с
= 2 МГц
Из приведенных рисунков 7-10 видно:
1) значения уровней боковых лепестков ФН ЛЧМ сигналов изменяются по закону Sinc
(х);
2) величина доплеровского сдвига по частоте не существенно влияет на значение
главного лепестка ФН;
3) энергетические составляющие спектра ФН ЛЧМ сигналов распределены равномерно
и имеют примерно одинаковые значения.
Таким образом ФН ЛЧМ сигналов обладают свойством инвариантности к
доплеровскому рассогласованию по частоте, они также обеспечивают минимум затрат
частотно-временных ресурсов инфокоммуникационных систем из-за высокой
равномерности распределения энергетических составляющих в частотной области.
Однако, ЛЧМ сигналы имеют малый ансамбль слабокоррелированных форм.
14.
В настоящее время усилия специалистов в области инфокоммуникационных системнаправлены на исследование эффективности канальных сигналов, созданных на основе
специальных кодов и новых методов расширения спектра. В, частности, специалистами
факультета был предложен один из таких классов сигналов (ПС ЛЧМ), в котором
объединены положительные свойства как ЛЧМ сигналов, так и псевдослучайных
последовательностей (ПСП). Указанный класс сигналов имеет большой объем
слабокоррелированных
форм
при
сохранении
свойства
инвариантности
к
допплеровскому
рассогласованию
по
частоте
а,
следовательно,
позволяет
минимизировать затраты частотно-временных ресурсов за счет рационального
использования выделенной частотной полосы с обеспечением одновременного
информационного обмена для большего количества абонентов.
Математическая запись этого сигнала достаточно сложна, поэтому здесь приведен
только его вид в графической форме.
Анализ особенности формы огибающих функции взаимной неопределенности ПС ЛЧМ
сигналов:
позволил установить, что при модуляции ЛЧМ радиоимпульсов по задержке с помощью
ПСП с различным числом элементов (Ni ≠ Nj) максимальный уровень бокового выброса
огибающей ФВН не превышает величины
k
Ni N j
где k – коэффициент, характеризующий число совпадений моментов возникновения
одинаковых по значению элементов ПСП у различных ПС ЛЧМ сигналов (число
совпадений моментов возникновения ЛЧМ радиоимпульсов).
15.
Представляет также практический интерес передача сложных сигналов с помощьючастотно-временного кодирования.
Формирование этого класса сигнала происходит следующим образом: создается
последовательность из М непрерывно следующих друг за другом элементарных
сигналов. При этом условимся, что порядок следования элементарных сигналов
может быть любым, но каждый из таких сигналов должен входить в
последовательность только один раз. При таком формировании последовательности
её длительность равна
а ширина занимаемой полосы частот (ширина спектра последовательности)
f э ( M 1) f 0 1 0
такой сигнал иногда называют составным. Величина базы этого сигнала равна
Бс f э 0 M 1 ( M 1) f 0 0
Осуществляя перестановку элементарных сигналов, можно получать различные
последовательности, состоящие из М элементов (рисунок 11).
16.
Строки этой матрицы соответствуют разным частотам элементарных сигналов, астолбцы – разным временным позициям этих сигналов. Сигналы в одной строке имеют
одну и ту же частоту и разное временное положение, а сигналы в одном столбце – одно
и то же временное положение и различные частоты. Каждый элемент матрицы
представляет собой элементарный сигнал, соответствующий данной временной и
частотной позициям.
При формировании различных последовательностей на них, как правило, налагаются
различные ограничения. Например, в каждой последовательности используются
только те элементарные сигналы, которые относятся к разным столбцам и строкам, а
использование более одного сигнала из каждой строки и столбца запрещается. Число
различных перестановок элементов квадратной матрицы размером М при соблюдении
указанных ограничений равно М!
Практическое применение сложных сигналов
Применение сложных сигналов позволяет в ряде случаев решать задачи передачи
информации более успешно по сравнению с традиционными методами. К таким
случаям можно отнести:
передачу
информации
по
каналам
с
многолучевым
эффектом
распространения;
ослабление мешающего действия различных систем, работающих в том же
диапазоне частот;
повышение эффективности использования выделенного диапазона частот;
ослабление влияния узкополосных помех и т. п.
Кроме этого, сложные сигналы открывают ряд возможностей построения систем с
такими свойствами, которые не могут быть получены в системах с узкополосными
сигналами: скрытность, крипто - и имитостойкость связи; возможность одновременно с
передачей информации измерять координаты движущегося объекта и т. д.
17.
Применение сложных сигналов в многолучевых каналахЭффект многолучевого распространения в каналах со случайными параметрами
приводит к появлению интерференции между соседними посылками сигнала и их
замираниям. При простых сигналах влияние интерференции можно уменьшить, только
увеличивая длительность посылок, что, естественно, приводит к уменьшению скорости
передачи. Для ослабления существенных замираний уровня простые сигналы
приходится принимать методами разнесенного приема.
Применение сложных сигналов в ряде случаев позволяет решить задачу ослабления
влияния интерференции и замираний более успешно. Рассмотрим для этого рисунок 12,
на котором показаны огибающие одной посылки сложного сигнала, пришедшей по трем
разным лучам.
Рисунок 12.
Полагаем, что замирания являются общими и за время, равное длительности посылки
τо, амплитуда и начальная фаза элементов сигнала не меняются.
18.
Оптимальная обработка посылки сложного сигнала корреляторами или согласованнымифильтрами дает выходное напряжение, вид которого совпадает с корреляционной
функцией этой посылки. Выходные напряжения, соответствующие одной и той же
посылке и разным лучам, показаны на рисунке 12 б. Длительность основного лепестка
этого напряжения приблизительно равна величине
вых 1 / f э = 0 / Бс
Если база сигнала значительна (Бc»1), то τвых<τо
и, следовательно, в результате
обработки посылки происходит ее «сжатие» по времени. Нетрудно видеть, что выходные
напряжения разделяются друг от друга несмотря на то, что на входе посылки от разных
лучей перекрываются. Так как огибающие посылки, пришедшей по разным лучам Sx1,
Sx2, Sx3, случайны, то случайны и выходные напряжения Ux1 Uх2, Ux3.
Так как время запаздывания лучей и разность хода между ними случайны, то в общем
случае для их обработки необходимо применять линию с временем задержки равным
времени многолучевого растяжения сигнала, а отводы брать через интервалы, равные
минимальному времени запаздывания, которое определяется при экспериментальных
исследованиях свойств конкретного канала. Таким образом, применение сложных
сигналов позволяет разделить перекрывающиеся сигналы, приходящие по разным
лучам. Это дает возможность эффективно использовать энергию сигналов от отдельных
лучей и существенно ослабить влияние замираний, обусловленных эффектом
многолучевого распространения.
Применение сложных сигналов для борьбы с помехами
Применение сложных сигналов иногда позволяет эффективно бороться с различными
помехами, спектр которых сосредоточен в значительно более узком диапазоне частот по
сравнению с диапазоном, занимаемым спектром сложного сигнала.
19.
Как уже неоднократно указывалось, помехоустойчивость оптимального приема в2
гауссовских каналах зависит от величины
h0
E0 / N 0 ( Ps / Pш ) вх Б с
Для сложных сигналов с большим значением базы (Бс>1) требуемая величина ho, при
которой достигается заданная вероятность ошибки приема, может быть получена при
малом входном отношении мощности сигнала к мощности шума. Это означает, что
уровень сигнала на входе приемника оказывается значительно меньше уровня шума.
Если ввести условную величину Nо, характеризующую среднюю интенсивность
мощности сигнала на единицу полосы, то для сигнала с большой базой можно записать
условие
Чем больше база сигнала, тем сильнее посылка «замаскирована» в шумах. При таких
условиях обнаружить сам факт работы системы затруднительно. Так как мощность
сигнала в такой системе распределена в широкой полосе частот, то ее интенсивность
мала и такой сигнал практически не создает сколь - нибудь заметных помех системам, в
которых используются значительно более узкополосные сигналы. Работа систем с
узкополосными сигналами также не окажет существенного влияния на работу систем со
сложными сигналами, если применять фильтрацию той части спектра сложного сигнала,
где действует узкополосный сигнал. Потеря мощности сложного сигнала из-за такой
фильтрации при большой базе незначительны и не приводят к заметному уменьшению
величины напряжения после оптимальной обработки сложного сигнала.
Таким образом, применение сложных сигналов открывает возможность одновременной
работы в одном и том же диапазоне частот узкополосных и широкополосных систем без
заметного влияния их друг на друга (частотная совместимость систем).
Применение
сложных
сигналов
позволяет
также
улучшить
эффективность
использования отведенного диапазона частот, так как хорошие корреляционные
свойства ансамбля сложных сигналов позволяют успешно использовать такие сигналы
в системах, работающих одновременно в одном и том же диапазоне частот

















 electronics
electronics








